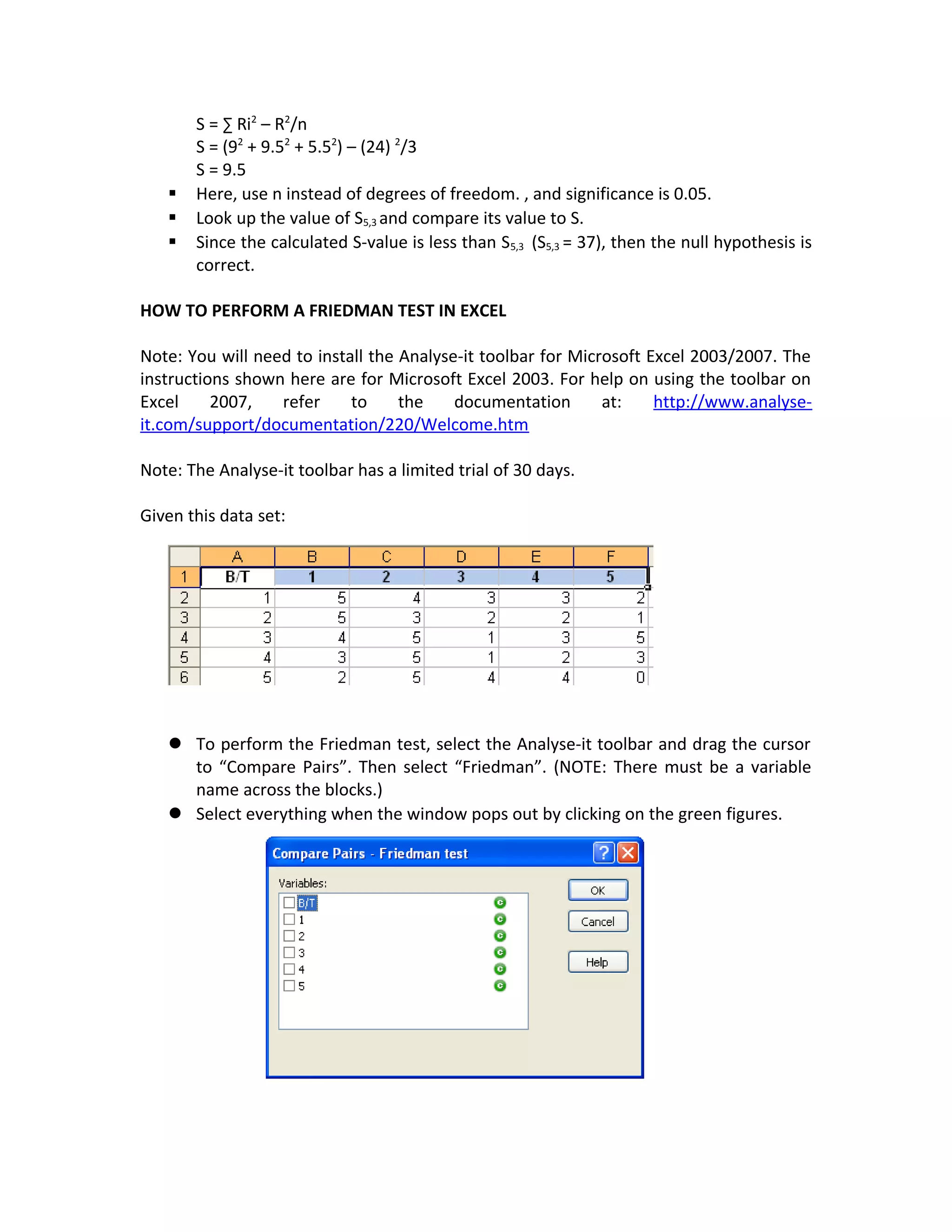
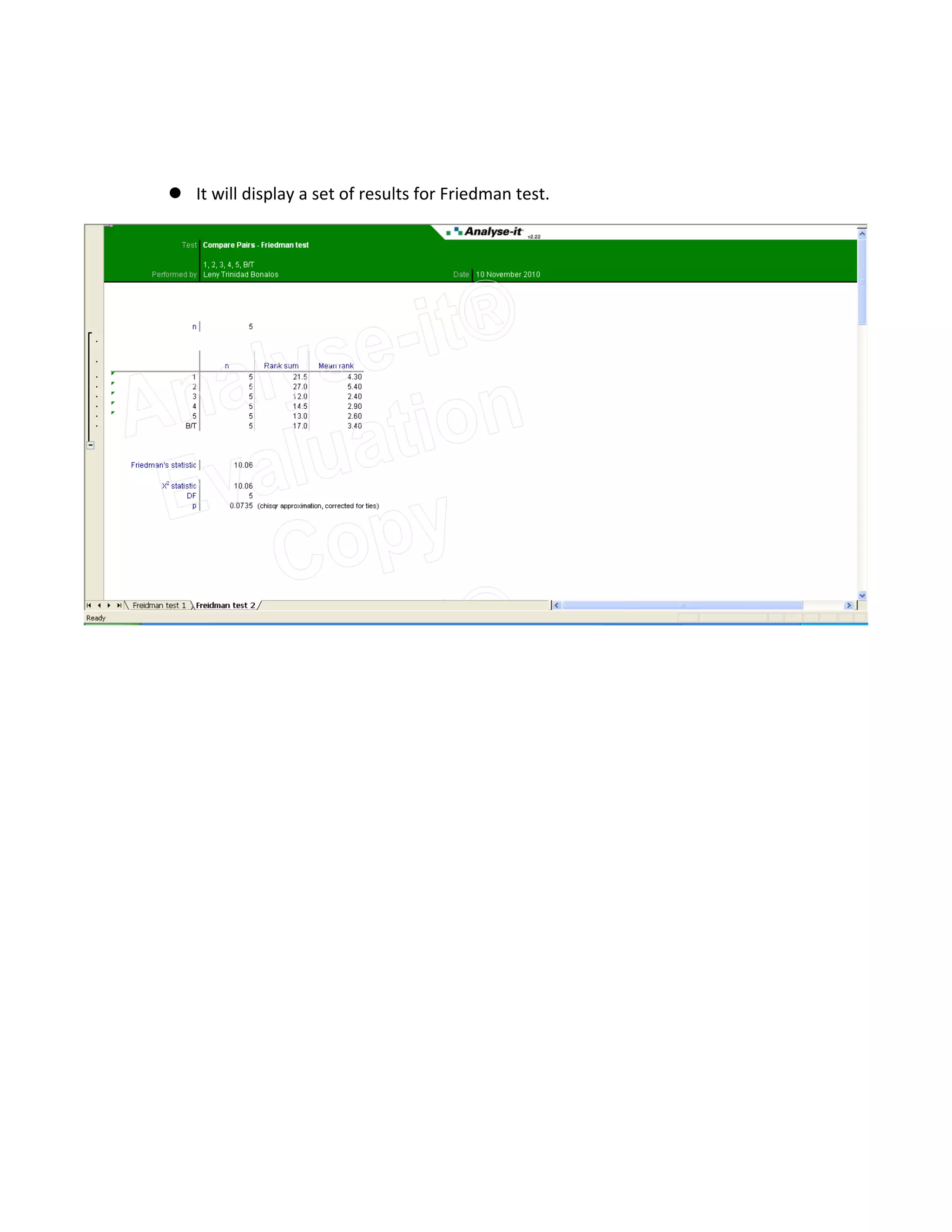
Friedman's test is a nonparametric test used to detect differences in treatments across multiple test blocks when using ordinal or ranked data. It involves ranking the data within each block, summing the ranks for each treatment, and calculating a Friedman test statistic that is compared to a chi-square critical value to determine if the null hypothesis that the treatments have identical effects can be rejected. An example demonstrates constructing a table with ranked data, calculating the Friedman statistic, determining the degrees of freedom, looking up the critical value, and comparing it to the statistic to evaluate the null hypothesis. The test can also be performed in Excel using the Analyse-it plugin.

1. F-TEST (FRIEDMAN’S TEST)
 Friedman's Test is a nonparametric hypothesis test, meaning that it is used to
study populations with rankings but no clear numerical interpretation.
 It is used when no distributional assumptions are necessary.
 This is used for three or more groups of data and the variables measured are
ordinally scaled.
 It is used to test the null hypothesis that the samples have been drawn from the
same population.
To use the F-test or Friedman’s test:
 State the null hypothesis (samples come from populations with equal
distributions) and the alternative hypothesis (samples come from populations
with different distributions).
 State the level of significance. This is the error probability.
 Set up a table based on the data. The rows represent the number of samples
(the blocks), while the columns represent the sample treatments.
 In the table, rank the data within the blocks, giving the lowest value rank 1 and
tied values the average of the two ranks.
 Get the sum of the ranks per treatment.
 Compute the Friedman test statistic, which is obtained through either formula:
S = ∑ Ri2
– R2
/n
where Ri2 is the sum of the squares of the rank sums, R2 is the square of the
total rank sum and n is the number of treatments.
Fr = 12/bt(t+1) * ∑Tj
2
– 3b(t + 1)
 where b is the number of blocks, t is the number of treatments, and ∑Tj
2
is the
sum of the squares of the rank sums.
 Test the null hypothesis by comparing the test statistic with the chi-square
critical value from the χ2
distribution table (if you used the first formula, find the
equivalent in the Friedman statistics table).
 To find the chi-square critical value mentioned above, subtract 1 from the
number of treatments to get the number of degrees of freedom. Look up the chi-
square value equivalent to the degrees of freedom and the significance level. Do
this is you calculated the test statistic with the second formula.

2.  If Fr is greater than or equal to the critical chi-square value/Friedman statistics
table value found, the null hypothesis is dropped.
EXAMPLE:
A nutritionist compared three treatments of squash-malunggay-banana baby food
preparations with the ingredients in different proportions. The three treatments
were subjected to a sensory evaluation using four evaluators. The treatments were
rated 1 to 4, 4 being the highest and best rating. Assume significance is 5%.
 State the hypotheses: Ho = samples are from same-distribution populations, Ha
= samples come from different-distribution populations.
 Create a table first, then list down all the data. Then rank the data across blocks
(in black) and find the sum (in red).
BlockTreatment Treatment
1
Treatment
2
Treatment
3
Block 1 3 (1.5) 4 (3) 3 (1.5)
Block 2 4 (3) 2 (1.5) 2 (1.5)
Block 3 3 (1.5) 4 (3) 3 (1.5)
Block 4 4 (3) 3 (2) 2 (1)
∑Rank 9 9.5 5.5
 Compute for the Friedman test statistic.
Fr = 12/bt(t+1) * ∑Tj
2
– 3b(t + 1)
Fr = 12/(4)(3)(3+1) * ∑Tj
2
– 12(3 + 1)
Fr = 12/(4)(3)(3+1) * ∑Tj
2
– 12(3 + 1)
Fr = 12/(4)(3)(3+1) * (92
+ 9.52
+ 5.52
) – 12(3 + 1)
Fr = 2.375
 Next, find the degrees of freedom.
DOF = treatments – 1 = 3 – 1 = 2
 Look for the chi-square value with DOF 2 and significance level 0.05 (5%). This is
5.991.
 Compare the Fr and the chi-square value.
Since Fr < 5.991, the null hypothesis is then true.
OR
 After constructing the table, use the formula S = ∑ Ri2
– R2
/n.

3. S = ∑ Ri2
– R2
/n
S = (92
+ 9.52
+ 5.52
) – (24) 2
/3
S = 9.5
 Here, use n instead of degrees of freedom. , and significance is 0.05.
 Look up the value of S5,3 and compare its value to S.
 Since the calculated S-value is less than S5,3 (S5,3 = 37), then the null hypothesis is
correct.
HOW TO PERFORM A FRIEDMAN TEST IN EXCEL
Note: You will need to install the Analyse-it toolbar for Microsoft Excel 2003/2007. The
instructions shown here are for Microsoft Excel 2003. For help on using the toolbar on
Excel 2007, refer to the documentation at: http://www.analyse-
it.com/support/documentation/220/Welcome.htm
Note: The Analyse-it toolbar has a limited trial of 30 days.
Given this data set:
 To perform the Friedman test, select the Analyse-it toolbar and drag the cursor
to “Compare Pairs”. Then select “Friedman”. (NOTE: There must be a variable
name across the blocks.)
 Select everything when the window pops out by clicking on the green figures.

4.  It will display a set of results for Friedman test.