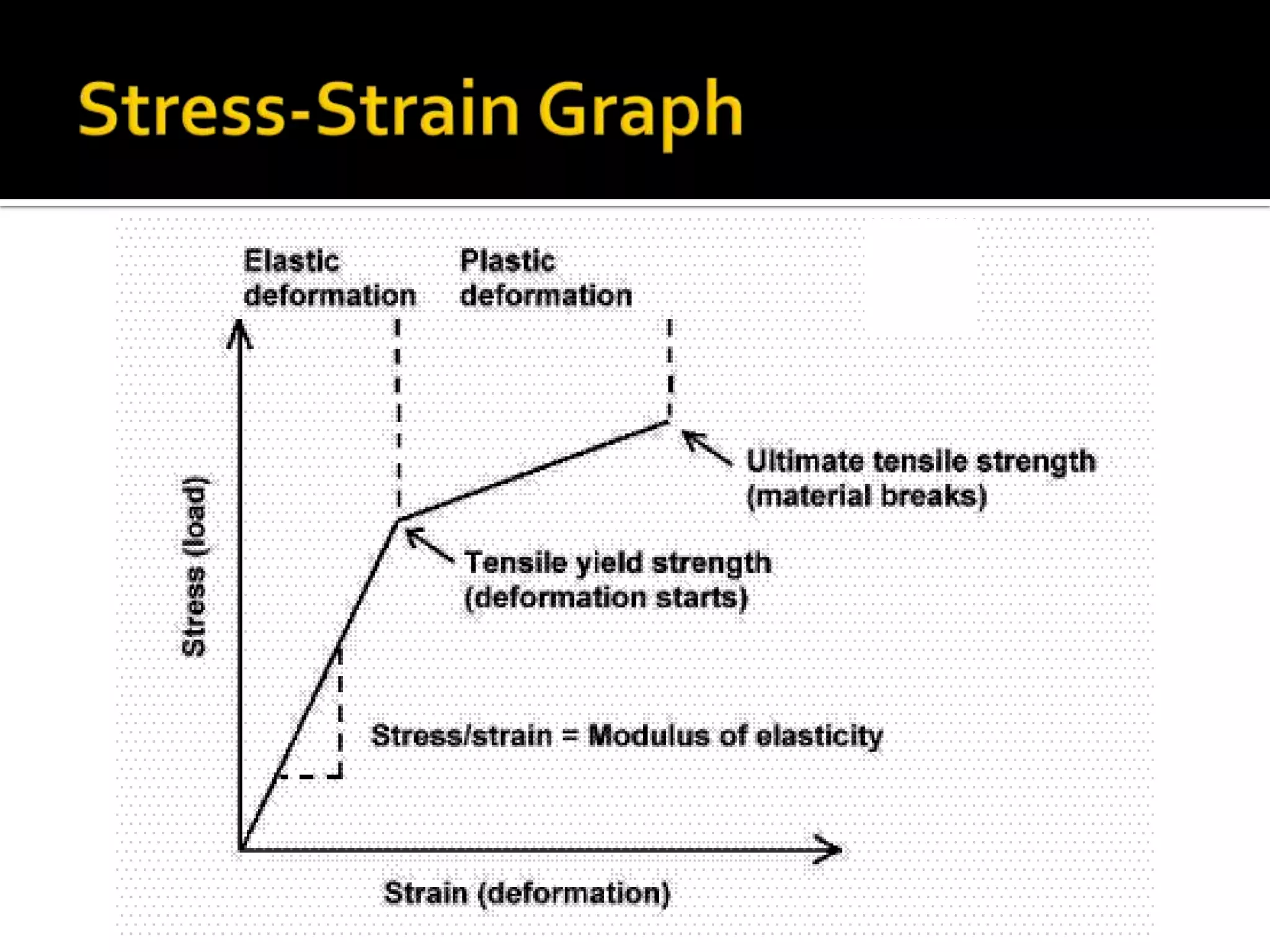
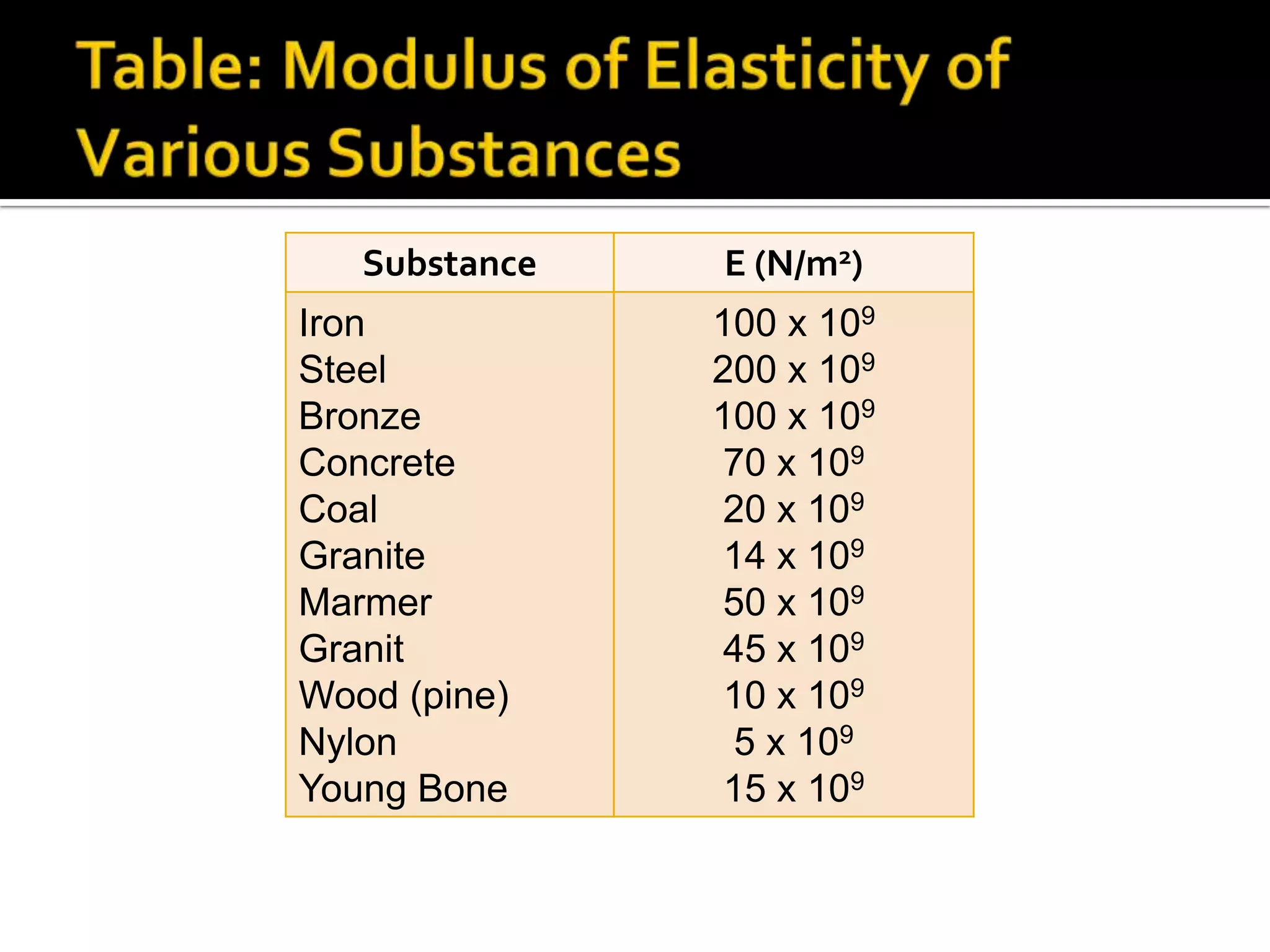
1) Elasticity is the ability of an object to return to its original shape after an external force is removed. 2) Hooke's Law states that the extension of a spring is proportional to the load applied, and the spring's force constant defines this proportionality. 3) Simple harmonic motion occurs when there is a restoring force proportional to displacement that causes an object to oscillate around the equilibrium position.

1. Elasticity and Simple Harmonic MotionDewi MuliyatiDepartment of Physics State University of Jakarta

2. Outline…Stress, Strain, and Modulus of ElasticityHooke’s LawForce Constant of Elastic ObjectsRestoring ForceEquation for Displacement in SHMPeriod of SHMHooke’s Law for Spring ArrangementSeveral Benefits of Springs

3. !!!Elasticity is the ability of an object to return to its original shape as soon as the external force which is applied to the object is eliminated (relieved).

4. Stress, Strain, and Modulus of ElasticityCourse-1

5. A Pulling Stress, σIs defined as the quotient between the pulling force F experienced by the wire and its cross-sectional area (A).

6. Strain, eIs defined as the quotient between the change in length ∆L and its initial length L.

7. Stress-Strain Graph

8. Modulus of Elasticity, EThe modulus of elasticity, E of a material is defined as the stress-strain ratio experienced by the material.

9. Table: Modulus of Elasticity of Various Substances

10. Hooke’s LawCourse-1

11. Hooke’s LawIf the pulling force does not exceed the spring’s elastic limit, then the spring’s length increase is directly proportional to the pulling force.

12. Force Constant of Elastic ObjectsCourse-1

13. Force Constant of Elastic ObjectsE is the modulus of elasticity of material (N/m2)L is the length of object, no force applied (m)A is the cross-sectional area (m2)

14. Restoring ForceCourse-2

15. Restoring ForceThe force whose magnitude is proportional to displacement and always acts in the opposite direction of displacement (position).The restoring force always causes an object to move back and forth about the equilibrium point (simple harmonic motion).The restoring force is always opposite to the displacement direction (motion) of the object.

16. Equation for Displacement in SHMCourse-2

17. Equation for Displacement in SHMDisplacement equationθ0 , the initial phase angle is obtained from the initial condition.A is amplitude.ω is angular frequency.

18. Period of SHMCourse-2

19. Period of SHMAcceleration of SHM,Angular Frequency,Period,

20. Hooke’s Law for Spring ArrangementCourse-2

21. Serial spring arrangementFor the special case of two springs with constants k1 and k2,the spring constant of replacement spring, ks:

22. Parallel spring arrangementFor n identical springs in a parallel arrangement, where every spring has a force constant k, the replacement spring constant kp:

23. Several Benefits of SpringsCourse-2

24. Suspension systems in Motor Vehicles to Damped Shocks

25. Springs on steering wheels