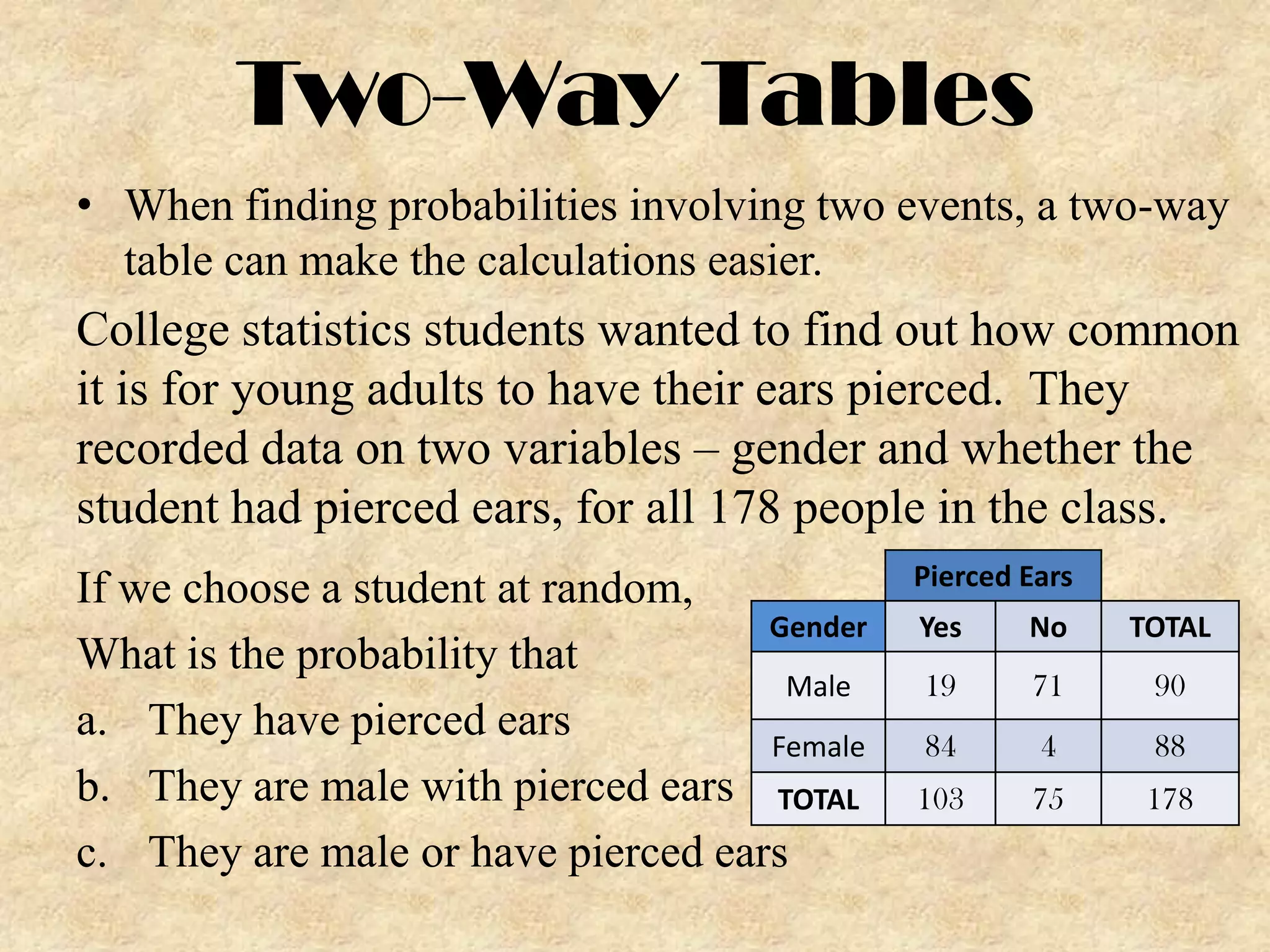
Students in a college statistics class collected data on 178 students' gender and whether their ears were pierced. They recorded this information in a two-way table to calculate probabilities. The two-way table showed that of the 90 male students, 19 had pierced ears. Of the 88 female students, 84 had pierced ears. The probabilities of being male with pierced ears, having pierced ears, or being male or having pierced ears can be determined from this two-way table.

1. Two-Way Tables
• When finding probabilities involving two events, a two-way
table can make the calculations easier.
College statistics students wanted to find out how common
it is for young adults to have their ears pierced. They
recorded data on two variables – gender and whether the
student had pierced ears, for all 178 people in the class.
If we choose a student at random,
Gender
What is the probability that
Male
a. They have pierced ears
Female
b. They are male with pierced ears TOTAL
c. They are male or have pierced ears
Pierced Ears
Yes
No
TOTAL
19
71
90
84
4
88
103
75
178

2. Venn-Diagrams
• If events A and B are not mutually exclusive, they can occur
together
• The probability that one or the other occurs is less than the
sum of their probabilities

3. Venn-Diagrams
• A Venn diagram takes of the double counting problem using
the General Addition Rule of Two Events:
P(A or B) = P(A) + P(B) – P (A and B)
If two events are mutually exclusive, the P(A and B) = 0
- This is just a special case of the addition rule
since P(A and B) = 0, we are subtracting nothing
P(A or B) = P(A) + P(B)

4. Venn-Diagrams
Vocabulary and Standard Notation:
• The complement of an event AC contains
the outcomes that are not in A
• Events A and B are mutually
exclusive (disjoint) if they do
not overlap, that have no
outcomes in common.

5. Venn-Diagrams
Vocabulary and Standard Notation:
• The event A and B is the intersection
of A and B, and it is notated as
A∩B
• The event A or B is the union of
A and B, and it is notated as
AUB

6. Venn-Diagrams
The notation that will be used on the AP Exam that is also on
the equation sheet:
P(A U B) = P(A) + P(B) – P(A ∩ B)
or
and
• A U B represents union (or)
• A ∩ B represents intersection (and)
Pg. 306-307