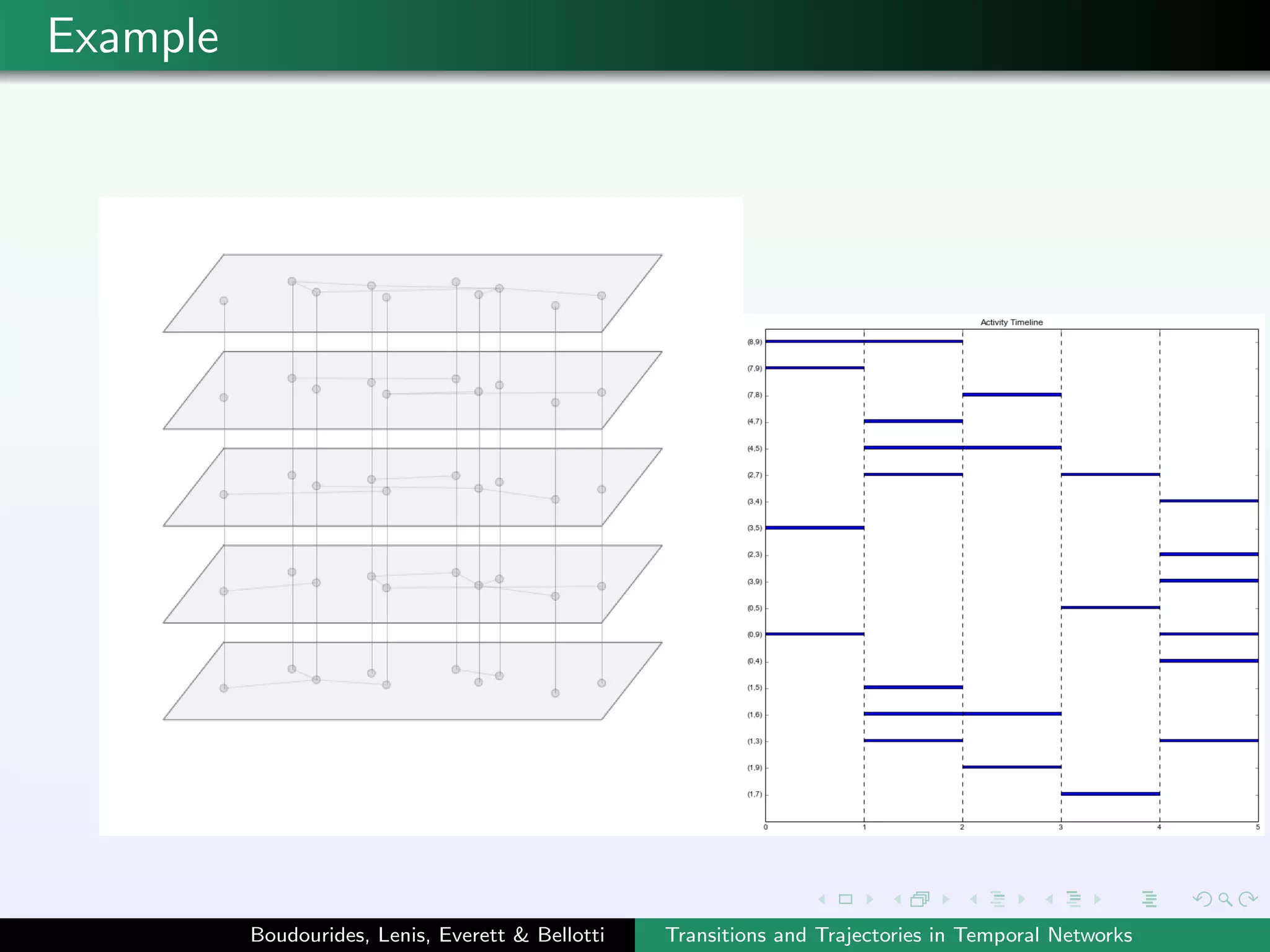
This document describes computational tools for analyzing transitions and trajectories in temporal networks. It defines key concepts such as edges and vertices having activity timelines, transitions occurring when edges become active/inactive at the same time, and trajectories being alternating sequences of translations and transitions that vertices undergo. Python code is provided to generate temporal networks, display transitions and trajectories, and output trajectory statistics.

1. Transitions and Trajectories
in Temporal Networks
Moses A. Boudourides1 & Sergios T. Lenis2
with Martin Everett & Elisa Bellotti
Department of Mathematics
University of Patras, Greece
1Moses.Boudourides@gmail.com
2sergioslenis@gmail.com
12 June 2015
Examples and Python code:
http://mboudour.github.io/2015/06/12/Transitions-&-Trajectories-in-Temporal-Networks.html
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

2. Overview
The terms “graph” and “(social) network” are used here interchangeably.
This is an elaboration of Borgatti & Halgin’s analysis of
trajectories in temporal networks.
Using Python’s NetworkX, we have developped a
computational tool
generates a random temporal network,
displays a plot of this temporal network as a multilayer graph
(layers corresponding to time slices),
displays the activity timelines of all edges in this graph,
computes all transitions induced by co–incident eges,
computes all trajectories of vertices formed by alternating
translations and transitions and
presents the table of statistics of all trajectories.
The Python scripts for all these computations are available at:
https://github.com/mboudour/TrajectoriesOfTemporalGraphs
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

3. Basic Concepts and Notation
By a temporal network we understand an ordinary network,
in which edges and vertices are not active or present in all
time, but for certain time points inside a given time period
(time interval) T. In general, T ⊂ R+ and time points can be
either isolated points or (sub)intervals (of nonnegative real
numbers).
We denote by V , E the (finite) sets of vertices and edges,
respectively, of a temporal network.
Let (u, v) ∈ E be an arbitrary edge joining two vertices
u, v ∈ V . We denote by T(u,v), Tu, Tv ⊂ T the activity time
set of edge (u, v) and vertices u, v, respectively, and we
assume the following consistency condition to hold, for all
edges (u, v) and vertices u, v:
T(u,v) ⊆ Tu ∩ Tv .
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

4. The activity timeline of edge (u, v) is defined as a function
α(u,v) : T(u,v) −→ {0, 1} such that
α(u,v)(t) =
1, whenever t ∈ T(u,v),
0, whenever t ∈ T T(u,v).
Similarly, the activity timeline of vertex u is defined as a
function αu : Tu −→ {0, 1} such that
αu(t) =
1, whenever t ∈ Tu,
0, whenever t ∈ T Tu.
Furthermore, given a vertex u and a time point τ ∈ Tu, we
write uτ in order to denote the (activated) vertex u at time τ.
In other words, if τ ∈ T(u,v), i.e., α(u,v)(τ) = 1, then
τ ∈ Tu ∩ Tv , αuτ (τ) = αvτ (τ) = 1, where (uτ , vτ ) is an edge
of the temporal network.
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

5. Example
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

6. To avoid certain technicalities, let us assume (from now on)
that we have a temporal network such that, for any edge or
vertex, the activity time set of this edge or vertex is a union of
disjoint intervals (each one having positive length).
Thus, for any edge e, the activity set Te of e is:
Te =
k
n=1
Tn(e).
Above k = k(e) and, for all n = 1, . . . , k, Tn(e) is a closed
interval of the form:
Tn(e) = [tn(e), tn(e)],
where tn(e), tn(e) ≥ 0, for n = 1, . . . , k, and:
tn(e) < tn(e) < tn+1(e).
Tn(e) is called n–th activity subinterval of the activity set Te
and tn(e), tn(e) are its left, right end points (respectively).
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

7. Note that, in this way, T becomes the convex hull (i.e., the
minimum closed interval) containing the union of all activity
subintervals of all edges of the temporal network:
T = conv
e∈E
k
n=1
Tn(e) .
Any t ∈ T e∈E
k
n=1 Tn(e) is called intermitting
time point.
Furthermore, we denote by Ie the set of all end points of all
subintervals of Te, i.e.,
Ie = t0(e), t0(e), t1(e), t1(e), . . . , tk(e), tk(e) .
Lumping together all sets Ie, for all edges e, one gets the
total set of all end points of the temporal network
I =
e∈E
Ie.
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

8. Definition
Let τ ∈ I. Then τ is called:
intermediate time point when, for every edge e ∈ E, if
τ ∈ Tn(e), for some n, then τ is always an interior point of
Tn(e).
co–terminal time point when, for every edge e ∈ E, if
τ ∈ Tn(e), for some n, then τ is always either the left or the
right end point of Tn(e) (but always the same for all edges),
t t tτ τ τ
e e e
f f f
intermediate time τ left co–terminal time τ right co–terminal time τ
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

9. Definition
Let e, f be two edges and let τ ∈ Te ∪ Tf . Then τ is called:
anti–terminal time point (w.r.t. e, f ) when τ is the right
(or left) end point of Tn(e), for some n, and the left (right,
resp.) end point of Tm(f ), for some m,
step–like time point (w.r.t. e, f ) when τ is is an interior
point of Tn(e), for some n (or an interior point of Tm(f ), for
some m) and an end point of Tm(f ), for some m (or an end
point of Tn(e), for some n, resp.).
t tτ τ
e e
f f
anti–terminal time τ step–like time τ
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

10. Definition of Transitions
Definition
Let u be a vertex of the temporal network and v, w two neighbors
of u. If τ ∈ T(u,v) ∪ T(u,w) is such that τ is either an anti–terminal
or a step–like time point (w.r.t. (u, v), (u, w)), then we say that u
passes from v to w at time τ through a transition denoted as
vτ
uτ
−→ wτ .
t tτ τ
Transition vτ
uτ
−→ wτ
(u, v) (u, v)
(u, w) (u, w)
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

11. Examples of Transitions
In the following diagramm, there are 12 transitions of u
through its neighbors v, w, z:
v2
u2
−→ w2, v3
u3
−→ z3, w3
u3
−→ z3, v4
u4
−→ z4,
w4
u4
−→ z4, z6
u6
−→ v6, z6
u6
−→ w6, v8
u8
−→ w8,
v8
u8
−→ z8, w10
u10
−→ v10, w10
u10
−→ z10, z10
u10
−→ v10.
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

12. Definition of Translations
Definition
Let u, v two adjacent vertices in the temporal network. If
τ, σ ∈ T(u,v), τ < σ, are such that [τ, σ] ⊂ [ti (u, v), ti (u, v)], for
some activity subinterval [ti (u, v), ti (u, v)], then we say that u
shifts from vτ to vσ through a translation denoted as vτ
u
vσ.
tti τ σ ti
Translation vτ
u
vσ
(u, v)
Remarks:
In a temporal network, neither transitions nor translations make up edges.
However, if two vertices are joined by a transition, it is possible (but not
necessary) that these vertices were joined by an edge too.
In a temporal network without self–loops, any two vertices joined by a
translation cannot be joined by an edge.
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

13. Definition of Trajectories
Definition
In a temporal network, a trajectory of vertex u passing over its
neighbors v, w, z, . . . is an alternating sequence of vertices,
translations and transitions of the form:
[(v0, u, v1), (v1, u1, w1), (w1, u, w2), (w2, u2, z2), . . .]
where v0
u
v1 is a translation, v1
u1
−→ w1 is a transition,
w1
u
w2 is a translation, w2
u2
−→ z2 is a transition, etc.
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks

14. Example: Two Trajectories
t0 1 2 3 4
Trajectory [(v0, u, v1), (v1, u1, w1), (w1, u, w2), (w2, u2, v2), (v2, u, v3), (v3, u3, w3), (w3, u, w4)]
(u, v)
(u, w)
t0 1 2 3 4
Trajectory [(v0, u, v3), (v3, u3, w3), (w3, u, w4)]
(u, v)
(u, w)
Boudourides, Lenis, Everett & Bellotti Transitions and Trajectories in Temporal Networks