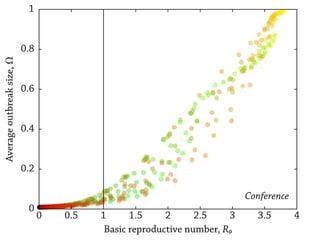
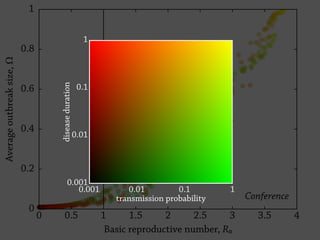
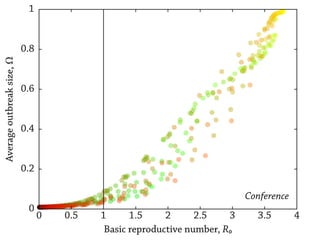
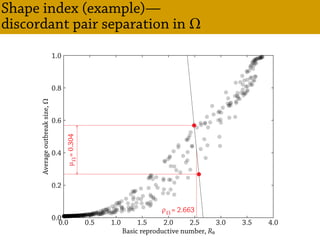
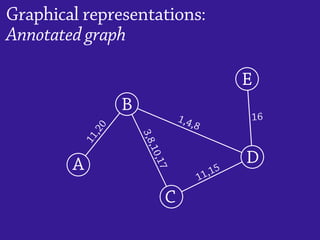
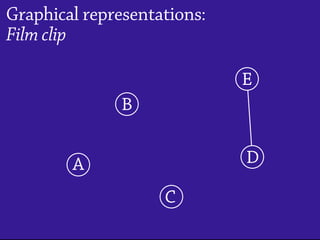
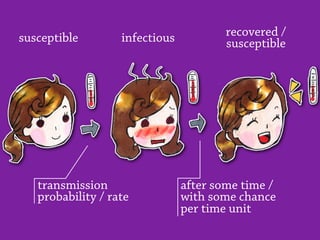
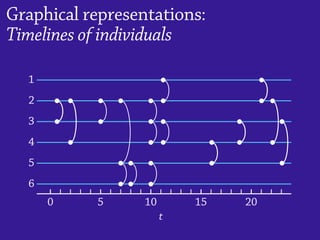
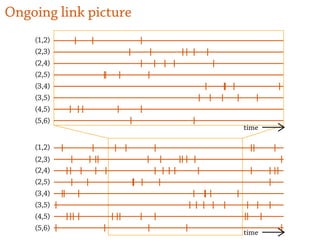
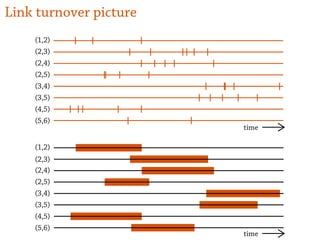
Temporal networks provide a framework for modeling systems of interactions that occur between nodes over time. These networks capture both the topological structure of connections as well as the timing of interactions. Three key aspects of temporal networks discussed in the document are: 1) Temporal networks can be represented using contact sequences that capture when interactions occur between nodes, unlike static networks which only represent connections. 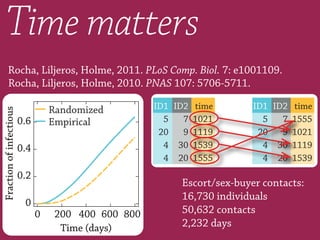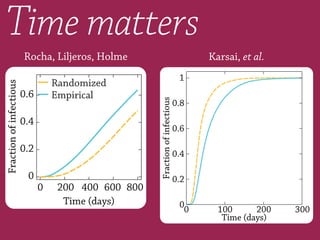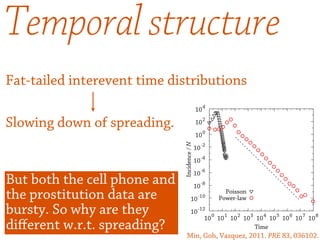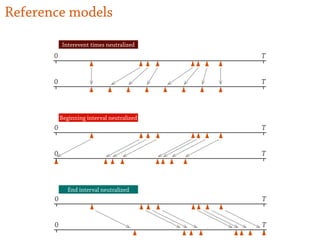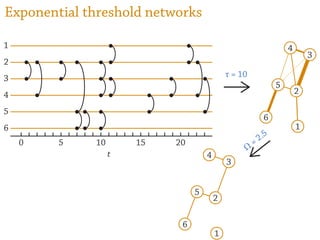2) The temporal structure of interactions, such as patterns in the timing of contacts, can impact dynamical processes unfolding on the network like information or disease spreading. 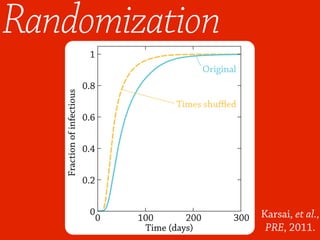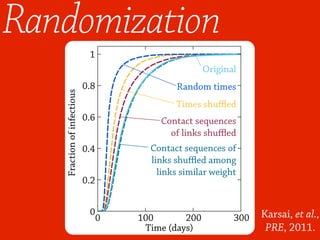3) Randomizing the timing of contacts in empirical temporal network data can alter dynamical processes, highlighting the importance of temporal structure beyond just topology.

1. Temporal networks
of human interaction
Petter Holme

3. Ntriangles = 3
Among the people we study,
there is a tendency for
triangles to form.

4. Ntriangles = 3
Rumors would spread slowly
because of the many
triangles.

5. Time & topology

7. time

8. network

9. Human interaction

10. What are we interested in?
Something that can:
. . . be measured relatively easy
(who are involved & when).
. . . and give scientific insights.
Examples:
-Two persons being close to each other.
-Two persons doing things together.
-One person sending a message to another.
Human interaction

11. Two persons being close to each other
-RFID tags.
-Smartphones / Bluetooth.
-Smartphones / GPS.
-Campus Wi-fi.
-Hospital records.
-Co-tagged in images.
-Public transportation.
-Sexual contacts (via Internet mediated prostitution).
Human interaction

12. Two persons doing things together
(not necessarily close)
-Paper co-authorships.
-Movie actors.
-Criminal co-offenders.
One person sending a message to another
-E-mails.
-Internet forums.
-Instant messaging.
Human interaction

13. Representations

14. Numerical representations:
Contact sequences
ID1
2
6
2
10
7
3
5
2
7
10
ID2
4
8
8
11
2
5
3
10
3
2
time
10
10
15
20
22
25
30
30
31
34

15. Numerical representations:
Interval graphs
ID1
2
6
2
10
7
3
5
2
7
10
ID2
4
8
8
11
2
5
3
10
3
2
time interval
(10,15)
(11,14)
(18,19)
(20,22)
(20,24)
(20,30)
(25,31)
(40,45)
(40,50)
(51,53)

16. 0 5 10 15 20
1
2
3
4
5
6
t
Graphical representations:
Timelines of individuals

17. (1,2)
(1,3)
(1,4)
(2,3)
Graphical representations:
Timelines of links

18. Graphical representations:
Annotated graph
E
D
C
B
A
11,20
1,4,8
3,8,10,17
11,15
16

19. Graphical representations:
Film clip
E
D
C
B
A
E
D
C
B
A

22. Epidemiology

27. transmission
probability / rate
after some time /
with some chance
per time unit
susceptible infectious recovered /
susceptible

28. +

29. Time matters

30. Time matters
E
D
C
B
A
11,20
1,4,8
3,8,10,17
11,15
16

31. Time matters
Rocha, Liljeros, Holme, 2010. PNAS 107: 5706-5711.
Escort/sex-buyer contacts:
16,730 individuals
50,632 contacts
2,232 days

32. 1555
ID1 ID2 time
5 7 1021
20 9 1119
4 30 1539
ID1 ID2 time
5 7 1555
20 9 1021
4 30 1119
4 20 15394 20
Time matters
Rocha, Liljeros, Holme, 2010. PNAS 107: 5706-5711.
Escort/sex-buyer contacts:
16,730 individuals
50,632 contacts
2,232 days
Rocha, Liljeros, Holme, 2011. PLoS Comp. Biol. 7: e1001109.
0
0.2
0.4
0.6
0 200 400 600
Fractionofinfectious
Time (days)
Empirical
800
0
0.2
0.4
0.6
0 200 400 600
Time (days)
Empirical
Randomized
800
Fractionofinfectious

33. Time matters

34. Time matters
0
0.2
0.4
0.6
0 200 400 600
Time (days)
Empirical
Randomized
800
Fractionofinfectious
1
0.8
0.6
0.4
0.2
0
0 100 200 300
Time (days)
Fractionofinfectious
Rocha, Liljeros, Holme Karsai, et al.

35. Physics Reports 519 (2012) 97–125
Contents lists available at SciVerse ScienceDirect
Physics Reports
journal homepage: www.elsevier.com/locate/physrep
Temporal networks
Petter Holmea,b,c,⇤
, Jari Saramäkid
a
IceLab, Department of Physics, Umeå University, 901 87 Umeå, Sweden
b
Department of Energy Science, Sungkyunkwan University, Suwon 440–746, Republic of Korea
c
Department of Sociology, Stockholm University, 106 91 Stockholm, Sweden
d
Department of Biomedical Engineering and Computational Science, School of Science, Aalto University, 00076 Aalto, Espoo, Finland
a r t i c l e i n f o
Article history:
Accepted 1 March 2012
Available online 6 March 2012
editor: D.K. Campbell
a b s t r a c t
A great variety of systems in nature, society and technology – from the web of sexual
contacts to the Internet, from the nervous system to power grids – can be modeled as
graphs of vertices coupled by edges. The network structure, describing how the graph is
wired, helps us understand, predict and optimize the behavior of dynamical systems. In
many cases, however, the edges are not continuously active. As an example, in networks
of communication via e-mail, text messages, or phone calls, edges represent sequences
of instantaneous or practically instantaneous contacts. In some cases, edges are active for
non-negligible periods of time: e.g., the proximity patterns of inpatients at hospitals can
be represented by a graph where an edge between two individuals is on throughout the
time they are at the same ward. Like network topology, the temporal structure of edge
activations can affect dynamics of systems interacting through the network, from disease
contagion on the network of patients to information diffusion over an e-mail network. In

36. 1
ISBN 978-3-642-36460-0
Understanding Complex Systems
Petter Holme
Jari Saramäki Editors
Temporal
Networks
TemporalNetworksHolme·SaramäkiEds.
Understanding Complex Systems
Petter Holme · Jari Saramäki Editors
Temporal Networks
The concept of temporal networks is an extension of complex networks as a modeling
framework to include information on when interactions between nodes happen. Many
studies of the last decade examine how the static network structure affect dynamic
systems on the network. In this traditional approach the temporal aspects are pre-
encoded in the dynamic system model. Temporal-network methods, on the other hand,
lift the temporal information from the level of system dynamics to the mathematical
representation of the contact network itself. This framework becomes particularly
useful for cases where there is a lot of structure and heterogeneity both in the timings
of interaction events and the network topology. The advantage compared to common
static network approaches is the ability to design more accurate models in order to
explain and predict large-scale dynamic phenomena (such as, e.g., epidemic outbreaks
and other spreading phenomena). On the other hand, temporal network methods are
mathematically and conceptually more challenging. This book is intended as a first
introduction and state-of-the art overview of this rapidly emerging field.
Physics
9 7 8 3 6 4 2 3 6 4 6 0 0

37. Randomization

38. Randomization
Times shuffled
Original
1
0.8
0.6
0.4
0.2
0
0 100 200 300
Time (days)
Fractionofinfectious
Karsai, et al.,
PRE, 2011.

39. Randomization
Times shuffled
Original
1
0.8
0.6
0.4
0.2
0
0 100 200 300
Time (days)
Fractionofinfectious
Karsai, et al.,
PRE, 2011.
Random times
Times shuffled
Original
Contact sequences of
links shuffled among
links similar weight
Contact sequences
of links shuffled
1
0.8
0.6
0.4
0.2
0
0 100 200 300
Time (days)
Fractionofinfectious

40. Temporal structure

41. Temporal structure
Fat-tailed interevent time distributions
Slowing down of spreading.
10-12
10
-10
10
-8
10
-6
10
-4
10
-2
10
0
10
2
10
4
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
Poisson
Power-law
Time
Incidence/N
Min, Goh, Vazquez, 2011. PRE 83, 036102.
But both the cell phone and
the prostitution data are
bursty. So why are they
different w.r.t. spreading?

44. Europhys. Lett., 64 (3), pp. 427–433 (2003)
EUROPHYSICS LETTERS 1 November 2003
Network dynamics of ongoing social relationships
P. Holme(∗
)
Department of Physics, Ume˚a University - 901 87 Ume˚a, Sweden
(received 21 July 2003; accepted in final form 22 August 2003)
PACS. 89.65.-s – Social and economic systems.
PACS. 89.75.Hc – Networks and genealogical trees.
PACS. 89.75.-k – Complex systems.
Abstract. – Many recent large-scale studies of interaction networks have focused on networks
of accumulated contacts. In this letter we explore social networks of ongoing relationships with
an emphasis on dynamical aspects. We find a distribution of response times (times between
consecutive contacts of different direction between two actors) that has a power law shape over a
large range. We also argue that the distribution of relationship duration (the time between the
first and last contacts between actors) is exponentially decaying. Methods to reanalyze the data
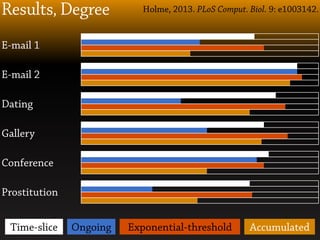
to compensate for the finite sampling time are proposed. We find that the degree distribution
for networks of ongoing contacts fits better to a power law than the degree distribution of
the network of accumulated contacts do. We see that the clustering and assortative mixing
coefficients are of the same order for networks of ongoing and accumulated contacts, and that
the structural fluctuations of the former are rather large.
Introduction. – The recent development in database technology has allowed researchers
to extract very large data sets of human interaction sequences. These large data sets are
suitable to the methods and modeling techniques of statistical physics, and thus, the last years
have witnessed the appearance of an interdisciplinary field between physics and sociology [1–3].
More specifically, these studies have focused on network structure —in what ways the networks

45. Limited communication capacity unveils
strategies for human interaction
Giovanna Miritello1,2
, Rube´n Lara2
, Manuel Cebrian3,4
& Esteban Moro1,5
1
Departamento de Matema´ticas & GISC, Universidad Carlos III de Madrid, 28911 Legane´s, Spain, 2
Telefo´nica Research, 28050
Madrid, Spain, 3
NICTA, Melbourne, Victoria 3010, Australia, 4
Department of Computer Science & Engineering, University of
California at San Diego, La Jolla, CA 92093, USA, 5
Instituto de Ingenierı´a del Conocimiento, Universidad Auto´noma de Madrid,
28049 Madrid, Spain.
Connectivity is the key process that characterizes the structural and functional properties of social networks.
However, the bursty activity of dyadic interactions may hinder the discrimination of inactive ties from large
interevent times in active ones. We develop a principled method to detect tie de-activation and apply it to a
large longitudinal, cross-sectional communication dataset (<19 months, <20 million people). Contrary to
the perception of ever-growing connectivity, we observe that individuals exhibit a finite communication
capacity, which limits the number of ties they can maintain active in time. On average men display higher
capacity than women, and this capacity decreases for both genders over their lifespan. Separating
communication capacity from activity reveals a diverse range of tie activation strategies, from stable to
exploratory. This allows us to draw novel relationships between individual strategies for human interaction
and the evolution of social networks at global scale.
any different forces govern the evolution of social relationships making them far from random. In recent
years, the understanding of what mechanisms control the dynamics of activating or deactivating social
SUBJECT AREAS:
SCIENTIFIC DATA
COMPLEX NETWORKS
APPLIED MATHEMATICS
STATISTICAL PHYSICS
Received
15 January 2013
Accepted
2 May 2013
Published
6 June 2013
Correspondence and
requests for materials
should be addressed to
E.M. (emoro@math.

46. time
time
(2,3)
(2,4)
(2,5)
(3,4)
(3,5)
(4,5)
(5,6)
(1,2)
(1,2)
(2,3)
(2,4)
(2,5)
(3,4)
(3,5)
(4,5)
(5,6)
Ongoing link picture

47. time
(2,3)
(2,4)
(2,5)
(3,4)
(3,5)
(4,5)
(5,6)
(1,2)
(1,2)
(2,3)
(2,4)
(2,5)
(3,4)
(3,5)
(4,5)
(5,6)
time
Link turnover picture

48. T0
T0
Beginning interval neutralized
T0
T0
Interevent times neutralized
End interval neutralized
T0
T0
Reference models

49. SIR on prostitution data
0
0.1
0.2
0.3
0.1 0.2 0.90.8 10.70.60.50.40.3
0.1
1
0.01
0.001
per-contact transmission probability
durationofinfection
Ω

50. SIR on prostitution data
0
0.1
0.2
0.3
0.1 0.2 0.90.8 10.70.60.50.40.3
0.1
1
0.01
0.001
per-contact transmission probability
durationofinfection
Ω
Interevent times neutralized

51. SIR on prostitution data
0
0.1
0.2
0.3
0.1 0.2 0.90.8 10.70.60.50.40.3
0.1
1
0.01
0.001
per-contact transmission probability
durationofinfection
Ω
Beginning times neutralized

52. SIR on prostitution data
0
0.1
0.2
0.3
0.1 0.2 0.90.8 10.70.60.50.40.3
0.1
1
0.01
0.001
per-contact transmission probability
durationofinfection
Ω
End times neutralized

53. SIR, average deviations
0
0.02
0.04
0.06
E-mail 1
0.1
0
0.05
Film
0
0.05
0.1
Dating 1
0.05
0.1
0.15
0.2
0
Forum
0
0.02
0.04
0.06
E-mail 2
0
0.02
0.06
0.08
0.04
Facebook
0
0.01
0.02
0.03
0.04
Prostitution
0
0.1
0.2
0.3
Hospital
0
0.04
0.06
0.08
0.02
Gallery
0
0.02
0.04
0.06
Conference
0.05
0.1
0
Dating 2
endtimes
beginningtimes
intereventtimes
Holme, Liljeros, 2014. Scientific Reports 4: 4999.

54. Temporal to static

55. Time-slice networks
tstart
tstop
0 5 10 15 20
1
2
3
4
5
6
t
1
2
3
4
5
6

56. Ongoing (concurrent) networks
tstart
tstop
0 5 10 15 20
1
2
3
4
5
6
t
1
2
3
4
5
6

57. Exponential threshold networks
0 5 10 15 20
1
2
3
4
5
6
t
1
2
3
4
5
6
1
2
3
4
5
6
Ω
= 2.5
τ = 10

58. Static Temporal
Evaluate by comparing ranking of vertices
Run SIR and measure
the expected outbreak
size Ωi if the i is the
source.
Measure predictors of
i’s importance. (Degree
ki and coreness ci.)
Calculate the rank correlation between Ωi and ki.
Higher correlation → better static representation.

59. E-mail 1
E-mail 2
Dating
Gallery
Conference
Prostitution
Results, Degree
Time-slice Ongoing Exponential-threshold Accumulated
Holme, 2013. PLoS Comput. Biol. 9: e1003142.

60. R₀

61. R₀ — basic reproductive number,
reproduction ratio, reproductive
ratio, ...
e expected number of secondary
infections of an infectious individual in
a population of susceptible individuals.

62. One of few concepts that
went from mathematical
to medical epidemiology

63. Disease R₀
Measles 12–18
Pertussis 12–17
Diphtheria 6–7
Smallpox 5–7
Polio 5–7
Rubella 5–7
Mumps 4–7
SARS 2–5
Influenza 2–4
Ebola 1–2

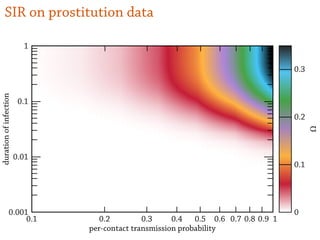
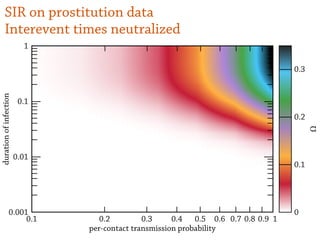
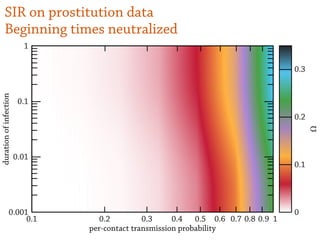
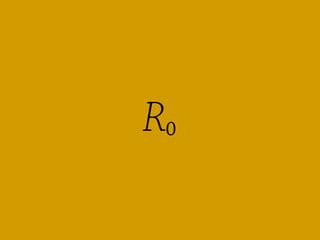
64. SIR model
ds
dt
= –βsi—
di
dt
= βsi – νi—
= νi
dr
dt
—
S I I I
I R
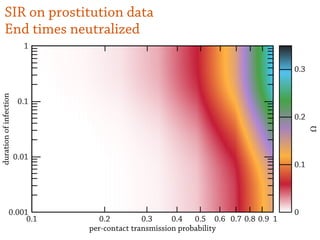
Ω = r(∞) = 1 – exp[–R₀ Ω]
where R₀ = β/ν
Ω > 0 if and only if R₀ > 1
e epidemic threshold

65. Problems with R₀
Hard to
estimate
Can be hard for
models
& even harder for outbreak data
and many datasets lack
the important early period
e threshold isn’t R₀ = 1 in practice
e meaning of a threshold in a finite population.
In temporal networks, the outbreak size
needn’t be a monotonous function of R₀

66. Problems with R₀
Hard to
estimate
Can be hard for
models
& even harder for outbreak data
and many datasets lack
the important early period
e threshold isn’t R₀ = 1 in practice
e meaning of a threshold in a finite population.
e topic of this project
In temporal networks, the outbreak size
needn’t be a monotonous function of R₀

67. Plan
Use empirical
contact data
Simulate the entire
parameter space of
the SIR model
Plot Ω vs R₀
Figure out what temporal network
structure that creates the deviations

68. 1
0.8
0.6
0.4
0.2
0
0 0.5 1 1.5 2 2.5 3 3.5 4
Averageoutbreaksize,Ω
Basic reproductive number, R0
Conference

69. 1
0.8
0.6
0.4
0.2
0
0 0.5 1 1.5 2 2.5 3 3.5 4
Averageoutbreaksize,Ω
Basic reproductive number, R0
Conference
0.001 0.01 0.1 1
1
0.1
0.01
0.001
transmission probability
diseaseduration

70. 1
0.8
0.6
0.4
0.2
0
0 0.5 1 1.5 2 2.5 3 3.5 4
Averageoutbreaksize,Ω
Basic reproductive number, R0
Conference

71. Shape index (example)—
discordant pair separation in Ω
1.0
0.8
0.6
0.4
0.2
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Basic reproductive number, R0
Averageoutbreaksize,Ω
μΩ=0.304
ρΩ = 2.663

72. avg. fraction of nodes present when 50% of contact happened
avg. fraction of links present when 50% of contact happened
avg. fraction of nodes present at 50% of the sampling time
avg. fraction of links present at 50% of the sampling time
frac. of nodes present 1st and last 10% of the contacts
frac. of links present 1st and last 10% of the contacts
frac. of nodes present 1st and last 10% of the sampling time
frac. of links present 1st and last 10% of the sampling time
Time evolution
degree distribution, mean
degree distribution, s.d.
degree distribution, coefficient of variation
degree distribution, skew
Degree distribution
link duration, mean
link duration, s.d.
link duration, coefficient of variation
link duration, skew
link interevent time, mean
link interevent time, s.d.
link interevent time, coefficient of variation
link interevent time, skew
Link activity
Node activity
node duration, mean
node duration, s.d.
node duration, coefficient of variation
node duration, skew
node interevent time, mean
node interevent time, s.d.
node interevent time, coefficient of variation
node interevent time, skew
Other network structure
number of nodes
clustering coefficient
assortativity
Temporal network structure

73. Correlation between point-cloud shape & temporal
network structure
*
*
** ** ** **
**
*
**
**
**
*
∆R0
0
0.2
0.4
0.6
0.8
1
R²
Time evolution
Node activity Link activity
Degree
distribution
Network
structure
fLT
fNT
fLC
fNC
FLT
FNT
FLC
FNC
γNt
σNt
cNt
µNt
γNτ
σNτ
cNτ
µNτ
γLt
σLt
cLt
µLt
γLτ
σLτ
cLτ
µLτ
γk
σk
ck
µk
N C r

74. ***
**
∆Ω
0
0.2
0.4
0.6
0.8
1
R²
Time evolution
Node activity
Link activity
Network
structure
fLT
fNT
fLC
fNC
FLT
FNT
FLC
FNC
γNt
σNt
cNt
µNt
γNτ
σNτ
cNτ
µNτ
γLt
σLt
cLt
µLt
γLτ
σLτ
cLτ
µLτ
γk
σk
ck
µk
N C r
Degreedistribution
Correlation between point-cloud shape & temporal
network structure
Holme & Masuda, 2015,
PLoS ONE 10:e0120567.

75. Beyond
epidemiology

76. Information / opinion spreading
“Viral videos doesn’t spread like viruses.”
Actors does not necessarily get infected by only one other.
Karimi, Holme, 2013. Physica A 392: 3476–3483.
reshold models:
Takaguchi, Masuda, Holme, 2013. PLoS ONE 8: e68629.
Time can be incorporated in many ways.
Major conclusion: burstiness can speed up spreading.

77. ank you!

78. ank you!
Collaborators:
Naoki Masuda
Jari Saramäki
Fredrik Liljeros
Luis Rocha
Sungmin Lee
Fariba Karimi
Juan Perotti
Taro Takaguchi
Hang-Hyun Jo
Illustrations by:
Mi Jin Lee