Διακριτά Μαθηματικά ΙI: Εισαγωγή στη Συνδυαστική
Αυτό είναι το δεύτερο μέρος των σημειώσεων μου στο προπτυχιακό μάθημα των Διακριτών Μαθηματικών του Μαθηματικού Τμήματος του Πανεπιστημίου Πατρών (άνοιξη 2014). Το πρώτο τμήμα της εισαγωγής στην λογική είναι εδώ:
http://www.slideshare.net/MosesBoudourides/1-32613813


















![Υπενθύμιση Συμβολισμού
Για κάθε θετικό ακέραιο n, συμβολίζουμε με [n] το σύνολο των θετικών
ακέραιων που είναι μικρότεροι ή ίσοι του n, δηλαδή, [n] = {1,2,...,n}.
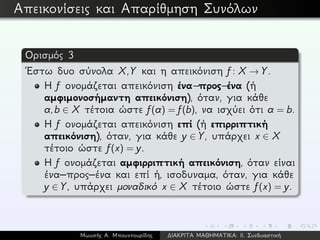
Ορισμός 4
´Ενα μη κενό σύνολο X ονομάζεται πεπερασμένο, όταν
υπάρχει ένας θετικός ακέραιος n και μια ένα–προς–ένα και
επί απεικόνιση ϕ: [n] → X. Στην περίπτωση αυτή, η
πληθικότητα (cardinality) του X, που ορίζεται ως το πλήθος
των στοιχείων του X, είναι n, δηλαδή, συμβολικά, |X| = n.
Επιπλέον, θέτουμε |∅| = 0.
Θεώρημα 5
´Εστω δυο πεπερασμένα σύνολα X,Y. Τότε
1 |X| ≤ |Y| αν και μόνον αν υπάρχει μια ένα–προς–ένα
απεικόνιση f: X → Y.
2 |X| ≥ |Y| αν και μόνον αν υπάρχει μια επί απεικόνιση
f: X → Y.
3 |X| = |Y| αν και μόνον αν υπάρχει μια ένα–προς–ένα και
επί απεικόνιση f: X → Y.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-24-320.jpg)
![Ακολουθίες και Λίστες
Ακολουθίες ως Απεικονίσεις
´Εστω X ένα (τυχόν) σύνολο και {xn}n=1,2,... μια αριθμήσιμη ακολουθία
στοιχείων του X. Η ακολουθία αυτή μπορεί να ταυτισθεί με μια
απεικόνιση, με την έννοια ότι αντιστοιχεί σε αυτή μια απεικόνιση
ϕ: N+ → X τέτοια ώστε, για κάθε n = 1,2,..., να είναι ϕ(n) = xn.
Αλλά, και αντίστροφα, σε κάθε απεικόνιση ϕ: N+ → X αντιστοιχεί η
ακολουθία {xn}n=1,2,..., όπου xn = ϕ(n), για κάθε n = 1,2,....
Ορισμός 6
´Εστω X ένα (τυχόν) σύνολο και n ένας θετικός ακέραιος.
Κάθε πεπερασμένη ακολουθία στοιχείων του X ονομάζεται
λίστα μήκους n (ή n–λίστα). ´Οπως παραπάνω, κάθε λίστα
n στοιχείων του X μπορεί να ταυτισθεί με μια απεικόνιση
ϕ: [n] → X τέτοια ώστε
η ϕ είναι ένα–προς–ένα, όταν τα στοιχεία της λίστας
είναι διακριτά (μη επαναλαμβανόμενα) και
η ϕ είναι ένα–προς–ένα και επί, όταν η λίστα
ταυτίζεται με το X, το οποίο υποτίθεται ότι είναι
πεπερασμένο σύνολο.3
3
Εξ ορισμού, ένα πεπερασμένο σύνολο δεν έχει επαναλαμβανόμενα
στοιχεία. Αν είχε θα ονομαζόταν πολυσύνολο.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-25-320.jpg)
![Μεταθέσεις και Συνδυασμοί
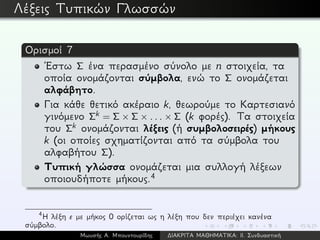
Ορισμός 8
∆οθέντους ενός περασμένου συνόλου X με n στοιχεία,
ονομάζουμε μετάθεση5 (permutation) του X (ή του [n])
κάθε ένα–προς–ένα και επί απεικόνιση από το σύνολο
X (ή το σύνολο [n]) στον εαυτό του.
Παρατηρήσεις:
Ας υποθέσουμε ότι το X έχει n στοιχεία. Τότε μια μετάθεση του X μπορεί
να θεωρηθεί ως:
Μια n–λίστα που σχηματίζεται από τα στοιχεία του X διατεταγμένα
με οποιοδήποτε τρόπο, αλλά χωρίς επαναλήψεις.
Με άλλα λόγια, κάθε μετάθεση του συνόλου X με n στοιχεία είναι μια
διατεταγμένη τοποθέτηση ενός από n αντικείμενα σε n θέσεις, έτσι
ώστε κάθε θέση να περιέχει ακριβώς ένα αντικείμενο.
5
Μερικές φορές, η μετάθεση καλείται διάταξη.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-27-320.jpg)

![Ορισμός 11
´Εστω ένα περασμένο σύνολο X με n στοιχεία και ένας
θετικός ακέραιος k ≤ n. Ονομάζουμε k–μετάθεση του X
(ή του [n]) κάθε k–λίστα διακριτών στοιχείων του X,
{xi}i=1,2,...,k, όπου xi ∈ X, για κάθε i ∈ [k], και xi = xj, για
κάθε i = j στο [k].
Θεώρημα 12
´Εστω n,k θετικοί ακέραιοι τέτοιοι ώστε n ≥ k και X
σύνολο n στοιχείων. Τότε το πλήθος των k–μεταθέ-
σεων του X (ή του [n]), που συμβολίζεται ως (n)k, είναι
ίσο με
(n)k = n(n − 1) · · · (n − k + 1) =
n!
(n − k)!
.
Απόδειξη: Προφανώς, έχουμε n επιλογές για τον πρώτο όρο της k–λίστας,
n − 1 για τον δεύτερο κ.ο.κ., έως ότου φθάσουμε στον k όρο, που είναι ο
τελευταίος, όπου θα έχουν μείνει n − k + 1 επιλογές.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-29-320.jpg)
![Πόρισμα 13
´Εστω n,k θετικοί ακέραιοι τέτοιοι ώστε n ≥ k και X σύνολο n στοιχείων.
Τότε το πλήθος των k–μεταθέσεων του X (ή του [n]), όταν επιτρέπονται οι
επαναλήψεις στοιχείων, είναι ίσο με nk.
Πόρισμα 14
Για ένα αλφάβητο με n σύμβολα και για κάθε θετικό ακέραιο k, υπάρχουν nk
λέξεις μήκους k (ενδεχομένως με επαναλαμβανόμενα σύμβολα).
Πρόταση 1
Το πλήθος όλων των υποσυνόλων ενός συνόλου αποτελούμενου από n
στοιχεία είναι 2n.
Απόδειξη: Αν κατασκευάσουμε μια απεικόνιση ένα–προς–ένα και επί μεταξύ του συνόλου όλων των
υποσυνόλων ένος συνόλου n στοιχείων και όλων των λέξεων μήκους n, που σχηματίζονται από το
δυαδικό αλφάβητο {0, 1}, τότε η Πρόταση θα είναι απόρροια του Θεωρήματος 5.3. Πράγματι, η
απεικόνιση αυτή κατασκευάζεται ως εξής: για κάθε A ⊂ [n], έστω f(A) η λέξη στο {0, 1}, της οποίας
το σύμβολο στην θέση i είναι 1, όταν i ∈ A, και 0, διαφορετικά. Προφανώς, f(A) ∈ {0, 1}n, για κάθε
A ⊂ [n], και αν, για δυο A, B ⊂ [n] έχουμε f(A) = f(B), τότε είναι εύκολο να ελεχθεί ότι A = B, δηλα-
δή, η f είναι ένα–προς–ένα. Επιπλέον, για κάθε λέξη w = {wi}i∈[n] ∈ {0, 1}n, υπάρχει ένα υποσύνο-
λο C ∈ [n] τέτοιο ώστε C = {i ∈ [n]: wi = 1}, δηλαδή, f(C) = w, ήτοι η f είναι και επί.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-30-320.jpg)
![Παράδειγμα: ´Εστω k θετικός ακέραιος. Το πλήθος όλων των θετικών
ακέραιων με k ψηφία είναι 9 · 10k−1.
Καθώς τώρα το αλφάβητο είναι το σύνολο {0,1,...,9}, προφανώς, έχουμε
9 επιλογές για τον πρώτο όρο ενός 9–ψήφιου αριθμού και, δεδομένου ότι
ακολούθως τα ψηφία μπορούν να επαναλαμβάνονται, υπάρχουν 10 επιλογές
για όλα τα άλλα ψηφία του αριθμού αυτού. ´Αρα, το ολικό πλήθος ψηφίων
είναι 9 · 10 · 10· · · · 10 = 9 · 10k−1.
Παράδειγμα: ´Εστω ότι κατασκευάζεται μια πόλη, στην οποία θα πρέπει να
υπάρχουν 10 διασταυρώσεις δρόμων. Κάποιες από τις διασταυρώσεις θα
έχουν φανάρια κυκλοφορίας και, σε κάποιες διασταυρώσεις με φανάρια, θα
υπάρχει επίσης και βενζινάδικο. Με πόσους τρόπους μπορεί αυτό να γίνει;
Θεωρούμε το αλφάβητο {A,B,C}, όπου το σύμβολο A αναπαριστά
διασταυρώσεις με φανάρια και βενζινάδικο, το B διασταυρώσεις μόνο με
φανάρια και χωρίς βενζινάδικο και το C διασταυρώσεις χωρίς ούτε φανάρια
ούτε βενζινάδικο. Τότε, κάθε 10–άδα διασταυρώσεων αναπαρίσταται ως
μια λέξη (λίστα) c = {ci}i∈[10] από το {A,B,C}, κάτι που σημαίνει ότι η
i–οστή διασταύρωση στην δεκάδα αυτή θα έχει φανάρια και βενζινάδικο,
όταν ci = A, θα έχει μόνο φανάρια, όταν ci = B, και δεν θα έχει ούτε
φανάρια ούτε βενζινάδικο, όταν ci = C (για κάθε i = 1,...,10). ´Ετσι,
σύμφωνα με το Πόρισμα 14, υπάρχουν 310 τέτοιες λέξεις, δηλαδή, 310
τρόποι κατασκευής των 10 διασταυρώσεων.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-31-320.jpg)
![Μεταθέσεις Πολυσυνόλου
Θεώρημα 15
´Εστω n,k,a1,a2,...,ak θετικοί ακέραιοι τέτοιοι ώστε
a1 + a2 + ... + ak = n και X πολυσύνολο7, που έχει n στοιχεία,
από τα οποία τα ai στοιχεία είναι τύπου i, για κάθε i ∈ [k].
Τότε το πλήθος των μεταθέσεων του πολυσυνόλου X είναι
ίσο με
n!
a1! · a2! · · · · · ak!
.
Απόδειξη: ´Εστω x το ζητούμενο πλήθος μεταθέσεων του πολυσυνόλου X. Επειδή τα στοιχεία κάθε
τύπου i (ξεχωριστά), έχουν ai! μεταθέσεις, για κάθε i ∈ [k], ο Κανόνας Γινομένου συνεπάγεται ότι
x · a1! · a2! · · · · · ak! είναι το πλήθος των μεταθέσεων του n, που φυσικά είναι ίσο με n!, οπότε
έπεται το ζητούμενο αποτέλεσμα.
Παράδειγμα: Με πόσους τρόπους μπορούν να διαταχθούν τα γράμματα
της λέξης MISSISSIPPI;
Για τη λέξη αυτή, n = 11, ενώ υπάρχουν k = 4 τύποι γραμμάτων (M, I, S, P) με
a1 = 1, a2 = 4, a3 = 4, a4 = 2. Επομένως, υπάρχουν 11!
4!4!2!1!
= 34650 διαφορετικοί τρόποι, με τους
οποίους τα γράμματα της λέξης MISSISSIPPI μπορούν να διαταχθούν.
7
Αυτό σημαίνει ότι το X μπορεί να έχει πολλαπλά στοιχεία.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-32-320.jpg)
![Συνδυασμοί
Ορισμός 16
´Εστω ένα περασμένο σύνολο X με n στοιχεία και ένας
θετικός ακέραιος k ≤ n. Ονομάζουμε k–επιλογή του X (ή του
[n]) κάθε υποσύνολο του X (ή του [n]), που έχει k στοιχεία.
Το πλήθος όλων των δυνατών k–επιλογών του X (ή του
[n]) ονομάζονται k–συνδυασμοί του X (ή του [n]) και
συμβολίζονται με n
k , το οποίο διαβάζεται ως ‘‘n ανά k’’ .8
Θεώρημα 17
´Εστω n,k ακέραιοι τέτοιοι ώστε n ≥ k ≥ 0 και X σύνολο
n στοιχείων. Τότε οι k–συνδυασμοί του X (ή του [n])
είναι ίσοι με
n
k
=
n!
k!(n − k)!
=
(n)k
k!
, για κάθε n > k > 0,
n
0
=
n
n
= 1.
8
Μερικές φορές, οι αριθμοί n
k ονομάζονται διωνυμικοί συντελεστές, όπως θα εξηγηθεί πιο κάτω.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-33-320.jpg)
![Απόδειξη: Πρώρα, ας θεωρήσουμε την περίπτωση n >k >0 και έστω (n)k
το πλήθος των k–μεταθέσεων του X. Φυσικά, τα στοιχεία κάθε μιας από
τις k–μεταθέσεις είναι διατεταγμένα, ενώ σε κάθε μια από τις k–επιλογές
(δηλαδή, σε κάθε υποσύνολο k στοιχείων του X) δεν χρειάζεται να υπάρχει
καμιά διάταξη. ´Ομως, σύμφωνα με το Θεώρημα 9, οι μεταθέσεις κάθε μιας
από τις k–επιλογές είναι k! (δηλαδή, κάθε υποσύνολο k στοιχείων του X
μπορεί να εμφανισθεί με k! τρόπους, στους οποίους τα στοιχεία του
υποσυνόλου έχουν διαφορετική διάταξη κάθε φορά). Επομένως, το συνολικό
πλήθος των k–μεταθέσεων (από τον Κανόνα του Γινομένου) θα ισούται με
το πλήθος όλων των δυνατών επιλογών (δηλαδή, με το πλήθος των
k–συνδυασμών) επί k!, ήτοι (n)k = n
k · k! και, καθώς (n)k = n · (n − 1) · · ·
(n − k + 1), παίρνουμε το ζητούμενο αποτέλεσμα. Τέλος, όταν k = 0 ή k = n,
τότε υπάρχει μια μοναδική k–επιλογή του [n] (το ∅ ή το [n], αντιστοίχως),
οπότε n
k = 1.9
9
Ουσιαστικά, ο τύπος των k–συνδυασμών μπορεί να επεκταθεί έτσι ώστε να ισχύει, για κάθε
k ∈ Z, αφού, όταν k < 0 ή k > n, τότε δεν υπάρχουν k–επιλογές του [n], οπότε παίρνουμε n
k = 0.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-34-320.jpg)

![Παράδειγμα: Σε ένα παιχνίδι τύχης, υπάρχουν 90 αριθμη-
μένα σφαιρίδια σε ένα δοχείο και επιλέγονται τυχαία 5 από
αυτά, τα οποία βγαίνουν από την κληρωτίδα όλα μαζί. Αν
κάθε λαχείο περιλαμβάνει μια πεντάδα αριθμών, στην οποία
ποντάρει ο παίκτης, πόσα λαχεία πρέπει να πάρει κανείς
για να κερδίσει;
Προφανώς, για να κερδίσει κανείς, πρέπει να ποντάρει σε όλα τα δυνατά 5–μελή υποσύνολα του
[90], τα οποία είναι 90
5 = 43 949 268.
Παράδειγμα: ´Ενας ασκούμενος γιατρός πρέπει να δουλέψει
στο νοσοκομείο πέντε μέρες μέσα στον Ιανουάριο, αλλά όχι
διαδοχικές μέρες. Με πόσους συνολικά διαφορετικούς τρό-
πους μπορεί να επιλέξει τις μέρες εργασίας του στο
νοσοκομείο;
´Εστω a1, a2, a3, a4, a5 οι μέρες εργασίας. Καθώς αυτές είναι 5 μέρες από 31, αλλά δεν μπορούν να
είναι διαδοχικές, θα έχουμε ότι 1 ≤ a1 < a2 − 1 < a3 − 2 < a4 − 3 < a5 − 4 ≤ 27. Αυτό σημαίνει ότι,
προφανώς, υπάρχει μια απεικόνιση ένα–προς–ένα και επί μεταξύ των 5–μελών υποσυνόλων του
[31], που δεν περιέχουν κανένα ζεύγος διαδοχικών αριθμών, και των 5–μελών υποσυνόλων του [27].
Επομένως, αντί να επιλέξει ένα 5–μελές υποσύνολο του [31] χωρίς διαδοχικούς αριθμούς, αρκεί να
επιλέξει ένα 5–μελές υποσύνολο του [27] και υπάρχουν 27
5 = 80 730 τρόποι να το κάνουμε αυτό.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-36-320.jpg)
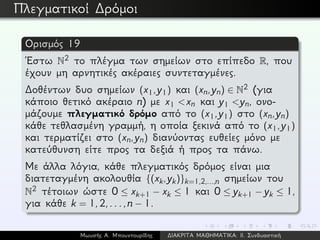
![Πρόταση 2
Για κάθε θετικούς ακέραιους k,m, το πλήθος των πλεγματικών
δρόμων από (0,0) ως (k,m) είναι ίσο με k+m
k . Με άλλα
λόγια, για n ≥ k, οι k–συνδυασμοί του [n] είναι ίσοι με το
πλήθος των πλεγματικών δρόμων από (0,0) ως (k,n − k).
Απόδειξη: Εξ ορισμού, κάθε πλεγματικός δρόμος από (0, 0) ως (k, m) αποτελείται από συνεχόμενα
μοναδιαία ευθύγραμμα τμήματα, τα οποία τα διανύει ο δρόμος αυτός σε κάθε βήμα. Επειδή κάθε
τέτοιο ευθύγραμμο τμήμα μπορεί να κατευθύνεται είτε προς δεξιά ή προς τα πάνω, αντιστοιχούμε σε
αυτό είτε το 1, όταν κατευθύνεται προς τα δεξιά, ή το 0, όταν κατευθύνεται προς τα πάνω. Με
άλλα λόγια, σε κάθε τέτοιο πλεγματικό δρόμο αντιστοιχούμε μια λίστα από 0 και 1, όπου το
συνολικό πλήθος των 1 μπορεί να είναι το πολύ ίσο με k, το οποίο είναι το μέγιστο πλήθος των
βημάτων, που ο δρόμος αυτός μπορεί να διανύσει κατευθυνόμενος προς τα δεξιά (εφόσον οι
κατευθύνσεις προς τα πάνω συνεισφέρουν μόνο με 0). Επιπλέον, το συνολικό πλήθος των μοναδιαίων
ευθυγράμμων τμημάτων, που σχηματίζουν, έναν τέτοιο πλεγματικό δρόμο είναι k + m. Επομένως,
υπάρχει μια απεικόνιση ένα–προς–ένα από το σύνολο όλων των δυνατών πλεγματικών δρόμων από
(0, 0) ως (k, m) και το σύνολο όλων των δυνατών k–επιλογών του [k + m]. Αλλά το πλήθος του
δεύτερου συνόλου είναι οι k–συνδυασμοί του [k + m], κάτι που ολοκληρώνει την απόδειξη.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-38-320.jpg)
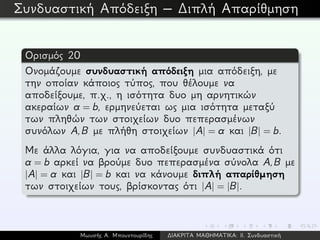
![Πρόταση 3
Για κάθε μη αρνητικούς ακέραιους n,k τέτοιους ώστε n ≥ k,
ισχύουν
n
k
=
n
n − k
.
Απόδειξη μέσω πλεγματικών δρόμων: Σύμφωνα με την Πρόταση 2, το
n
k
απαριθμεί το πλήθος
των πλεγματικών δρόμων από (0, 0) ως (k, n − k), ενώ το
n
n − k
απαριθμεί το πλήθος των
πλεγματικών δρόμων από (0, 0) ως (n − k, k). Αλλά οι δυο αυτές απαριθμήσεις πρέπει να
καταλήγουν στο ίδιο πλήθος, γιατί η ανάκλαση γύρω από την διαγώνιο (του επιπέδου) αντιστοιχεί
έναν πλεγματικό δρόμο από (0, 0) ως (k, n − k) σε έναν πλεγματικό δρόμο από (0, 0) ως (n − k, k).
Με άλλα λόγια, η ανάκλαση γύρω από την διαγώνιο αποτελεί μια απεικόνιση ένα–προς–ένα και επί
μεταξύ των συνόλων των δυο πλεγματικών δρόμων και, άρα, αυτά πρέπει να είναι ισοπληθή.
Απόδειξη μέσω του συμπληρώματος: Κατασκευάζουμε μια απεικόνιση f, που είναι ένα–προς–ένα και
επί, μεταξύ του συνόλου όλων των k–μελών υποσυνόλων του [n] και του συνόλου όλων των
n − k–μελών υποσυνόλων του [n] ως εξής. Για κάθε k–μελές υποσύνολο S του [n], θέτουμε f(S) = Sc
(το συμπλήρωμα του S στο [n]). Καθώς, για κάθε n − k–μελούς υποσυνόλου T του [n], υπάρχει
μοναδικό υποσύνολο S του [n] τέτοιο ώστε f(S) = T και φυσικά αυτό είναι το S = Tc, έπεται ότι η
απεικόνιση f είναι ένα–προς–ένα και επί, κάτι που αποδεικνύει τα δυο σύνολα, που απαριθμούνται
είτε ως
n
k
ή ως
n
n − k
, πρέπει να είναι ισοπληθή.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-40-320.jpg)
![Συνδυασμοί με Επαναλήψεις
Ορισμός 21
´Εστω ένα περασμένο σύνολο X με n στοιχεία και ένας
μη αρνητικός ακέραιος k. Ονομάζουμε k–επιλογή με
επαναλήψεις του X (ή του [n]) κάθε k–μελές πολυσύν-
ολο, που αποτελείται από στοιχεία του X (ή του
[n]).11 Το πλήθος όλων των δυνατών k–επιλογών με
επαναλήψεις του X (ή του [n]) ονομάζονται k–συνδυα-
σμοί με επαναλήψεις του X (ή του [n]).
Εναλλακτική ερμηνεία συνδυασμών με επαναλήψεις:
Ως το πλήθος των (x1,x2,...,xn) ∈ Nn τέτοιων ώστε
x1 + x2 + ... + xn = k, για κάθε n,k ∈ N.
11
Προφανώς, όταν k = 0, η 0–επιλογή δεν περιλάμβανει κανένα στοιχείο, δηλαδή, είναι το κενό
σύνολο.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-41-320.jpg)
![Θεώρημα 22
´Εστω n,k μη αρνητικοί ακέραιοι και X σύνολο n στοιχείων.
Τότε το πλήθος των k–συνδυασμών με επαναλήψεις του X (ή
του [n]) είναι
n + k − 1
k
=
n + k − 1
n − 1
.
Απόδειξη: Κάθε k–επιλογή με επαναλήψεις των n στοιχείων του X μπορεί να αναπαρασταθεί ως μια
συμβολική λίστα, η οποία αποτελείται από δυο ειδών σύμβολα: n − 1 διαχωριστικές γραμμές ‘‘|’’ και
k αστερίσκους ‘‘∗’’ . Οι n − 1 διαχωριστικές γραμμές σχηματίζουν n διαφορετικά κελιά, στα οποία
μπαίνουν οι αστερίσκοι, έτσι ώστε το i–οστό κελί να περιέχει έναν αστερικό αν και μόνον αν το
i–οστό στοιχείο του X περιέχεται στο πολυσύνολο της k–επιλογής. Για παράδειγμα, στο σύνολο 4
στοιχείων X = {a, b, c, d}, η 6–επιλογή που αντιστοιχεί στη συμβολική λίστα ∗ ∗ | ∗ || ∗ ∗∗ είναι το
πολυσύνολο {a, a, b, d, d, d}. Επομένως, το πλήθος αυτών των συμβολικών λιστών με n − 1 διαχωρι-
/ στικές γραμμές και k αστερίσκους είναι οι k–συνδυασμοί με επαναλήψεις των n στοιχείων του X.
´Ομως, το πλήθος αυτών των συμβολικών λιστών είναι ίσο με
n + k − 1
k
, επειδή κάθε συμβολική
λίστα αντιστοιχεί σε μια επιλογή k θέσεων, στις οποίες τοποθετούνται οι k αστερίσκοι, από τις
n + k − 1 θέσεις, που περιέχουν k αστερίσκους και n − 1 διαχωριστικές γραμμές. Επιπλέον, το πλήθος
αυτών των συμβολικών λιστών είναι επίσης ίσο με
n + k − 1
n − 1
, επειδή κάθε συμβολική λίστα αντι- /
στοιχεί σε μια επιλογή n − 1 θέσεων, όπου τοποθετούνται n − 1 διαχωριστικές γραμμές.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-42-320.jpg)
![Παράδειγμα: Σε ένα παιχνίδι τύχης, υπάρχουν 90
αριθμημένα σφαιρίδια σε ένα δοχείο και επιλέγονται τυχαία
5 από αυτά, σε 5 διαδοχικές τυχαίες κληρώσεις, με
επανατοποθέτηση όμως του σφαιριδίου, που έχει κληρωθεί
σε μια κλήρωση, πριν γίνει η επόμενη. Κερδίζει αυτός που
θα πετύχει το πολυσύνολο όλων των αριθμών, που βγάζει
έτσι η κλήρωση (ανεξάρτητα σειράς κλήρωσης). Αν κάθε
λαχείο περιλαμβάνει μια πεντάδα αριθμών, στην οποία
ποντάρει ο παίκτης, πόσα λαχεία πρέπει να πάρει κανείς
για να κερδίσει;
´Εστω b1, b2, b3, b4, b5 οι αριθμοί που κληρώνονται (γραμμένοι σε μη θφίνουσα σειρά). Καθώς αυτοί
είναι 5 από 90 αριθμούς, αλλά μπορούν να επαναλαμβάνονται, θα έχουμε ότι
1 ≤ b1 ≤ b2 ≤ b3 ≤ b4 ≤ b5 ≤ 90. ´Εστω λοιπόν X το σύνολο, του οποίου τα στοιχεία είναι 5 το
πολύ αριθμοί του [90], που μπορεί να επαναλαμβάνονται, αλλά πάντα θα είναι διατεταγμένοι με την
ανισο–ισότητα ‘‘≤.’’ Επιπλέον, έστω Y το σύνολο, του οποίου τα στοιχεία είναι 5 οποιοιδήποτε
αριθμοί του [94] (χωρίς καμία επανάληψη). Ισχυριζόμαστε ότι υπάρχει μια απεικόνιση f : X −→ Y,
που είναι ένα–προς–ένα και επί. Πράγματι, η απεικόνιση αυτή δίνεται από τη σχέση
f(b1, b2, b3, b4, b5) = (b1, b2 + 1, b3 + 2, b4 + 3, b5 + 4) και (b1, b2, b3, b4, b5) ∈ X αν και μόνον αν
(b1, b2 + 1, b3 + 2, b4 + 3, b5 + 4) ∈ Y. Επομένως, για να κερδίσει κανείς πρέπει να ποντάρει σε
94
5 = 54 891 018 λαχεία.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-43-320.jpg)
![Πίνακας Μεταθέσεων και Συνδυασμών
Μεταθέσεις
n διακριτά αντικείμενα n!
ai αντικείμενα τύπου i,
k
i=1 ai = n
n!
a1!·a2!···ak!
Λίστες
n διακριτά αντικείμενα σε
λίστα μήκους k
(n)k = n!
(n−k)!
ai διακριτά σύμβολα σε
λέξεις μήκους k
nk
Υποσύνολα
k–μελή υποσύνολα του [n]
n
k
k–μελή πολυσύνολα
με στοιχεία από το [n]
n + k − 1
k
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-44-320.jpg)
![Ασκήσεις
1 Πόσες απεικονίσεις υπάρχουν από το [n] στο [n]
που δεν είναι ένα–προς–ένα;
2 Αποδείξτε ότι το πλήθος των υποσυνόλων του [n]
με περιττό αριθμό στοιχείων είναι 2n−1.
3 Πόσοι πενταψήφιοι θετικοί ακέραιοι υπάρχουν
τέτοιοι ώστε το μεσαίο ψηφίο τους να είναι το 6 κι
οι αριθμοί αυτοί να είναι διαιρετοί με το 3;
4 Πόσοι πενταψήφιοι θετικοί ακέραιοι υπάρχουν
τέτοιοι ώστε να περιέχουν το ψηφίο 9 κι οι αριθμοί
αυτοί να είναι διαιρετοί με το 3;
5 Με πόσους τρόπους μπορούν να διαταχθούν τα
ψηφία {1,2,2,3,4,5,6} έτσι ώστε τα όμοια
στοιχεία να μη βρίσκονται σε διαδοχική σειρά;
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-45-320.jpg)

![12 Με πόσους τρόπους μπορούν να διαταχθούν τα
στοιχεία του [n] έτσι ώστε (1) το 1 να προηγείται
του 2 και το 3 του 4 και (2) το 1 να προηγείται
και του 2 και του 3;
13 Με πόσους τρόπους μπορούν να διαταχθούν τα
στοιχεία του [n] έτσι ώστε το άθροισμα κάθε δυο
διαδοχικών όρων της μετάθεσης να είναι περιττός
ακέραιος;
14 ´Εστω n = pa1
1 pa2
2 · · · pak
k , όπου τα pk είναι διακριτοί
πρώτοι, και τα ai είναι θετικοί ακέραιοι. Πόσους
θετικούς διαιρέτες έχει το n;
15 ´Εστω d(n) το πλήθος των θετικών διαιρετών του
n. (1) Για ποιους αριθμούς n είναι το d(n) δύναμη
του 2; (2) Ισχύει ότι, για κάθε θετικό ακέραιο n,
d(n) ≤ 1 + log2 n;
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-47-320.jpg)
![16 Με πόσους τρόπους μπορούμε να επιλέξουμε δυο
υποσύνολα A και B του [n] έτσι ώστε A ∩ B = ∅;
17 Με πόσους τρόπους μπορούμε να επιλέξουμε τρία
υποσύνολα A,B και C του [n] έτσι ώστε
A ⊆ C,B ⊆ C και A ∩ B = ∅;
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-48-320.jpg)

![Πόρισμα 24
Για κάθε μη αρνητικό ακέραιο n, το εναλλασσόμηνο άθροισμα
των διωνυμικών συντελεστών
n
k
είναι μηδέν. ∆ηλαδή,
n
k=0
(−1)k ·
n
k
xkyn−k = 0.
Απόδειξη: Θέτουμε στο ∆ιωνυμικό Θεώρημα x = −1 και y = 1.
Πόρισμα 25
Για κάθε μη αρνητικό ακέραιο n,
2n =
n
k=0
n
k
.
Απόδειξη: Και τα δυο σκέλη της ισότητας αυτής απαριθμούν το πλήθος του
συνόλου των υποσυνόλων του [n]. Στο αριστερό σκέλος, η αρίθμηση αυτή
γίνεται απευθείας, ενώ στο δεξιό σκέλος απαριθμούνται πρώτα όλα τα
k–μελή υποσύνολα του [n] και μετά αθροίζονται ως προς k. Εναλλακτικά, η
ισότητα αυτή απορρέει από το ∆ιωνυμικό Θεώρημα θέτοντας x = y = 1.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-50-320.jpg)
![Θεώρημα 26 (Ο Τύπος του Pascal )
Για κάθε μη αρνητικούς ακέραιους n και k,
n
k
+
n
k + 1
=
n + 1
k + 1
.
Απόδειξη: Εξ ορισμού, το αριστερό σκέλος της ισότητας, που θέλουμε να
αποδείξουμε, είναι ίσο προς το πλήθος των k + 1–μελών υποσυνόλων του
[n + 1]. Επιπλέον, το σύνολο όλων των k + 1–μελών υποσυνόλων του [n + 1]
διαμερίζεται σε δυο σύνολα: στο σύνολο S1 των k + 1–μελών υποσυνόλων
του [n + 1], κάθε ένα από τα οποία περιλαμβάνει το n + 1, και στο σύνολο
S2 των k + 1–μελών υποσυνόλων του [n + 1], κάθε ένα από τα οποία δεν
περιλαμβάνει το n + 1. Αφενός, τότε, κάθε στοιχείο του S1 θα είναι της
μορφής {n + 1} ∪ An, όπου το An είναι κάποιο k–μελές υποσύνολο του [n],
και, για αυτό, το πλήθος των στοιχείων του S1 θα είναι όσο ακριβώς είναι
το πλήθος των k–μελών υποσυνόλων του [n], δηλαδή,
n
k
. Από την άλλη
μεριά, το πλήθος των στοιχείων του S2 θα είναι όσο ακριβώς είναι το
πλήθος των k + 1–μελών υποσυνόλων του [(n + 1) − 1] = [n], δηλαδή,
n
k + 1
. Επομένως, η Αρχή του Αθρίσματος συνεπάγεται το επιθυμητό
αποτέλεσμα.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-51-320.jpg)

![Θεώρημα 28 (Η Ταυτότητα του Αθροίσματος)
Για κάθε μη αρνητικούς ακέραιους n,k με k ≤ n,
n
i=k
i
k
=
n + 1
k + 1
.
Απόδειξη: Το δεξιό σκέλος της προς απόδειξη ταυτότητας, προφανώς,
απαριθμεί τα k + 1–μελή υποσύνολα του [n + 1]. Αλλά και το αριστερό
σκέλος απαριθμεί τα ίδια υποσύνολα, χωρίζοντάς τα όμως σε υπο–ομάδες
σύμφωνα με το μεγαλύτερο στοιχείο τους. Πράγματι, δοθέντων των μη
αρνητικών n,k έτσι ώστε n ≥ k, έχουμε ότι, για κάθε i ≤ n − k, τα k + 1–μελή
υποσύνολα του [n + 1], των οποίων το μεγαλύτερο στοιχείο είναι το
k + i + 1, έχουν πλήθος ίσο με
k + i
k
, γιατί, όταν το μεγαλύτερο στοιχείο
ενός τέτοιου υποσυνόλου είναι το k + i + 1, τότε τα υπόποιπα στοιχεία του
πρέπει να αποτελούν ένα υποσύνολο του [k + i]. Επομένως, υπάρχουν
k
k
k + 1–μελή υποσύνολα του [n + 1] με μεγαλύτερο στοιχείο το k + 1,
k + 1
k
k + 1–μελή υποσύνολα του [n + 1] με μεγαλύτερο στοιχείο το k + 2 κ.ο.κ.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-53-320.jpg)

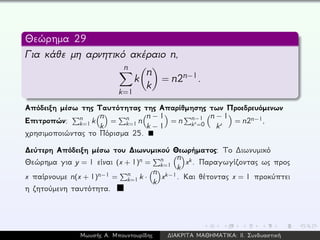
![Θεώρημα 30 (Η Ταυτότητα του Vandermonde)
Για κάθε μη αρνητικούς ακέραιους n,m,k με k ≤ min{n,m},
n + m
k
=
k
i=0
n
i
m
k − i
.
Απόδειξη: Το αριστερό σκέλος της προς απόδειξη ταυτότητας, προφανώς, απαριθμεί όλα τα k–μελή
υποσύνολα του [n + m]. Αλλά και το δεξιό σκέλος απαριθμεί τα ίδια υποσύνολα, χωρίζοντάς τα όμως
σε υπο–ομάδες σύμφωνα με το πλήθος στοιχείων που επιλέγονται από το [n]. Πράγματι, μπορούμε
να επιλέξουμε πρώτα i στοιχεία του [n] με
n
i
τρόπους και μετά να επιλέξουμε τα υπόλοιπα k − i
στοιχεία από το σύνολο {n + 1, n + 2, . . . , n + m} (τελικά, το [m]) με
m
k − i
τρόπους.
Πόρισμα 31
Για κάθε μη αρνητικό ακέραιο n,
2n
n
=
n
k=0
n
k
2
.
Απόδειξη: Η ταυτότητα του Vandermonde, για k = m = n, δίνει
2n
n
= n
i=0
n
k
n
n − i
=
n
i=0
n
i
2
(λόγω της Πρότασης 3).
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-56-320.jpg)

![Απόδειξη Πολυωνυμικού Θεωρήματος: Πρέπει να δείξουμε ότι ο όρος x
a1
1 x
a2
2 · · · x
ak
k μπορεί να
προκύψει με ακριβώς n
a1,a2,...,ak
τρόπους από το γινόμενο των k παραγόντων, που μπορούν να
ληφθούν ο καθένας σαν μια από τις παρενθέσεις του γινομένου (x1 + x2 + . . . + xk)n =
(x1 + x2 + . . . + xk) · · · (x1 + x2 + . . . + xk). Με άλλα λόγια, αρκεί να δείξουμε ότι για να πάρουμε
έναν τέτοιον όρο πρέπει να επιλέξουμε τα xi από ακριβώς i παρενθέσεις, για όλα τα i ∈ [k].
Ας πάρουμε λοιπόν ai φορές το xi, για όλα τα i ∈ [k], και ας διατάξουμε γραμμικά αυτούς τους
όρους. Το Θεώρημα 15 δείχνει ότι αυτό μπορεί να γίνει με ακριβώς n
a1,a2,...,ak
τρόπους. ´Ομως,
επιπλέον, κάθε γραμμική διάταξη p ορίζει έναν φυσικό τρόπο επιλογής παραγόντων από ένα
γινόμενο παρενθέσεων. Πράγματι, αν το j–ωστό σύμβολο της λέξης p είναι το xi, τότε επιλέγουμε το
xi από την j–ωστή παρέθεση. Με τον τρόπο αυτό, οι n
a1,a2,...,ak
γραμμικές διατάξεις θα
παραγάγουν ακριβώς n
a1,a2,...,ak
όρους ίσους προς x
a1
1 x
a2
2 · · · x
ak
k .
Προφανώς, η διαδικασία αυτή δημιουργεί μια απεικόνιση ένα–προς–ένα και επί μεταξύ, αφενός, του
συνόλου όλων των γραμμικών διατάξεων των n συμβόλων, από τα οποία τα ai είναι ίσα προς xi,
για όλα τα i ∈ [k], κι, αφετέρου, του συνόλου των όρων του (x1 + x2 + . . . + xk)n, οι οποίοι είναι ίσοι
προς x
a1
1 x
a2
2 · · · x
ak
k . Επομένως, ο συντελεστής του όρου x
a1
1 x
a2
2 · · · x
ak
k στο γινόμενο
(x1 + x2 + . . . + xk)n είναι ακριβώς ίσος προς n
a1,a2,...,ak
, όπως έπρεπε να δείξουμε.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-58-320.jpg)
![Θεώρημα 34
´Εστω n,a1,a2,...,ak μη αρνητικοί ακέραιοι, όπου k θετικός
ακέραιος, τέτοιοι ώστε n =
k
i=1 ai. Τότε, ισχύει13
n
a1,a2,...,ak
=
n
a1
· · ·
n − a1 − ... − ai
ai+1
· · ·
n − a1 − ... − ak−1
ak
.
Απόδειξη: Το αριστερό σκέλος της προς απόδειξη σχέσης απαριθμεί όλες τις γραμμικές διατάξεις ενός
πολυσυνόλου, που περιέχει το σύμβολο xi ai φορές, για όλα τα i ∈ [k]. Θα δείξουμε ότι και το δεξιό
σκέλος εκτελεί την ίδια ακριβώς απαρίθμηση. Πράγματι, ας επιλέξουμε πρώτα τις a1 θέσεις, στις
οποίες τοποθετείται το σύμβολο x1. Αυτό μπορεί να γίνει με n
a1
τρόπους. Στη συνέχεια, ας
επιλέξουμε τις a2 θέσεις, στις οποίες τοποθετείται το σύμβολο x2. Καθώς έχουν ήδη καταληφθεί a1
θέσεις, αυτό μπορεί να γίνει με n−a1
a2
τρόπους. Μετά, επιλέγουμε τις a3 θέσεις, στις οποίες
τοποθετείται το σύμβολο x3. Καθώς έχουν ήδη καταληφθεί a1 + a2 θέσεις, αυτό μπορεί να γίνει με
n−a1−a2
a3
τρόπους. Και ούτω καθ´ εξής, μέχρις ότου συμπηρωθούν όλες οι θέσεις για όλα τα
σύμβολα, οπότε παίρνουμε ότι και το συνολικό πλήθος όλων των δυνατών περιπτώσεων εκφράζεται
από το δεξιό σκέλος της ταυτότητας αυτής.
13
Παρατηρήστε ότι n − a1 − . . . − ak−1 = ak, οπότε ο τελευταίος όρος του δεξιού σκέλους της
σχέσης αυτής είναι ίσος προς ak
ak
= 1.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-59-320.jpg)

![4 Αποδείξτε ότι, για κάθε θετικό ακέραιο n, ισχύει
2n
n <4n.
5 Πόσα υποσύνολα του [n] είναι μεγαλύτερα από τα
συμπληρώματά τους;
6 Ποιος όρος του αναπτύγματος του
(x1 + x2 + ... + xk)k έχει τον μεγαλύτερο συντελεστή
κιαι ποιόν;
7 ´Εστω k και m μη αρνητικοί ακέραιοι και
n = 2m − 1. Αποδείξτε ότι το n
k είναι περιττό.
8 ´Εστω p ≥ 3 πρώτος ακέραιος και m και k < pm
θετικοί ακέραιοι. Αποδείξτε ότι το p είναι διαιρέτης
του pm
k .
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-61-320.jpg)


![Συνθέσεις και ∆ιαμερισμοί
Ορισμοί 35
´Εστω n,a1,a2,...,ak μη αρνητικοί ακέραιοι, όπου k
θετικός ακέραιος, τέτοιοι ώστε n = k
i=1 ai. Τότε, η
διατεταγμένη k–άδα (a1,a2,...,ak) ονομάζεται
ασθενής σύνθεση του n σε k μέρη και
σύνθεση του n σε k μέρη, εφόσον τα ai είναι θετικά,
για όλα τα i ∈ [k].
Παράδειγμα: Πόσες και ποιες είναι οι ασθενείς συνθέσεις και οι συνθέσεις
του 3 σε 2 μέρη;
Οι ασθενείς συνθέσεις του 3 σε 2 μέρη είναι οι εξής 4: (3,0),(0,3),(2,1),
(1,2) και οι συνθέσεις του 3 σε 2 μέρη είναι οι εξής 2: (2,1),(1,2).
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-64-320.jpg)
![Θεώρημα 36
Για κάθε θετικούς ακέραιους n και k, το πλήθος των
ασθενών συνθέσεων του n σε k μέρη είναι
n + k − 1
k − 1
=
n + k − 1
n
.
Απόδειξη: Το πρόβλημα είναι προφανώς ισοδύναμο με την απαρίθμηση του
πλήθους των τρόπων που n (όμοιες) μπάλλες μπορούν να τοποθετηθούν
μέσα σε k (διαφορετικά) κουτιά. Με όποιο τρόπο κι αν γίνει, η τοποθέτηση
δημιουργεί μια διατεταγμένη k–άδα αριθμών (που ο καθένας αντιστοιχεί
στο πλήθος των μπαλλών που έχουν μπει στο αντίστοιχο με την διάταξη
κουτί), των οποίων (αριθμών) το άθροισμα είναι ίσο προς n. Επομένως, το
πρόβλημα αναγάγεται στην εύρεση του πλήθους των k–συνδυασμών με
επαναλήψεις του [n], όπως έχει απαντηθεί από το Θεώρημα 22.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-65-320.jpg)
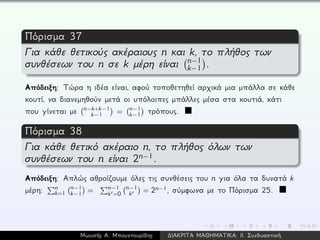
![Ορισμός 39
∆οθέντος ενός μη κενού συνόλου X, αν υπάρχει ένας θετικός
ακέραιος k και μια (πεπερασμένη) συλλογή {Ai}i∈[k] μη κενών
υποσυνόλων του X τέτοια ώστε τα Ai είναι ανά δυο ξένα,
δηλαδή, Ai ∩ Aj = ∅, για i,j ∈ [k],i = j, και X = ∪k
i=1Ai, τότε
λέμε ότι η συλλογή των υποσυνόλων Ai αποτελεί έναν
διαμερισμό του συνόλου X σε k υποσύνολα.
Ορισμός 40
Για κάθε θετικούς ακέραιους n,k, συμβολίζουμε με S(n,k)
το πλήθος των διαμερισμών του [n] σε k (μη κενά)
υποσύνολα και ονομάζουμε τα S(n,k) αριθμούς Stirling
δευτέρου είδους.
Παρατηρήσεις:
Για κάθε θετικό ακέραιο n, S(n,1) = S(n,n) = 1.
Για κάθε ακέραιο n ≥ 2, S(n,n − 1) = n
n−2 = n
2 .
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-67-320.jpg)
![Παράδειγμα: Υπάρχουν 6 διαμερισμοί του [4] σε 3 υποσύνολα, δηλαδή, S(4, 3) = 6.
Σύμφωνα με την προηγούμενη Παρατήρηση, S(4, 3) = 4
2 = 6. Για την ακρίβεια, οι 6 διαμερισμοί
είναι οι εξής: {{1, 2}, {3}, {4}}, {{1, 3}, {2}, {4}}, {{1, 4}, {2}, {3}}, {{2, 3}, {1}, {4}},
{{2, 4}, {1}, {3}}, {{3, 4}, {1}, {2}}.
Παράδειγμα: Υπάρχουν 25 διαμερισμοί του [5] σε 3 υποσύνολα, δηλαδή, S(5, 3) = 25.
Πρώτα, παρατηρούμε ότι υπάρχουν 2 τρόποι που το [5] μπορεί να διαμεριστεί σε 3 υποσύνολα: οι
πληθικότητες των διαμερισμών του [5] μπορούν να είναι είτε 3, 1, 1 ή 2, 2, 1. Στην πρώτη
περίπτωση, μπορούμε να επιλέξουμε τα στοιχεία που ανήκουν σε υποσύνολα πληθικότητας 3 με
5
3 = 10 τρόπους συνολικά, αφήνοντας φυσικά τα υπόλοιπα στοιχεία μέσα σε 2 υποσύνολα
πληθικότητας 1. Στην δεύτερη περίπτωση, καθώς όλοι οι διαμερισμοί τότε θα περιέχουν μόνο ένα
υποσύνολο πληθικότητας 1, υπάρχουν 5 τρόποι για να μοιρασθούν τα στοιχεία του [5] σε τέτοια
υποσύνολα (πληθικότητας 1). Επιπλέον, υπάρχουν 4
2 = 6 τρόποι για να διανεμηθούν τα υπόλοιπα
4 στοιχεία του [5] σε ένα υποσύνολο με 2 στοιχεία (πληθικότητας 2). ´Οταν όμως θέλουμε να
σχηματίσουμε 2 υποσύνολα πληθικότητας 2 (το καθένα), επειδή δεν έχει καμιά σημασία η διάταξη
αυτών των υποσυνόλων, θα πρέπει να κρατήσουμε τους μισούς τρόπους, 6/2 = 3, με τους οποίους
τα 4 στοιχεία του [5] διαμοιράζονται σε δυο υποσύνολα πληθικότητας 2 (το καθένα). Π.χ., αν είχαμε
ξεχωρίσει το {1} ως μονοσύνολο, τότε τα υπόλοιπα στοιχεία θα έμπαιναν σε έναν από τους εξής 3
διαμερισμούς: {{2, 3}, {4, 5}}, {{2, 4}, {3, 5}}, {{2, 5}, {3, 4}}. Επομένως, λόγω του κανόνα του
γινομένου, στην δεύτερη περίπτωση υπάρχουν 5 · 3 = 15 τρόποι διαμερισμού και, άρα, και στις δυο
περιπτώσεις μαζί, λόγω του κανόνα του αθροίσματος, υπάρχουν 10 + 15 = 25 τρόποι διαμερισμού
του [5] σε 3 υποσύνολα.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-68-320.jpg)
![Θεώρημα 41
Για κάθε θετικούς ακέραιους k ≤ n,
S(n,k) = S(n − 1,k − 1) + k · S(n − 1,k).
Απόδειξη: Θα κάνουμε μια συνδυαστική απόδειξη δείχνοντας ότι και τα δυο σκέλη της προς
απόδειξη ισότητας απαριθμούν τα ίδια πράγματα. Εξ ορισμού, το αριστερό σκέλος απαριθμεί το
πλήθος όλων των διαμερισμών του [n] σε k υποσύνολα. Από την άλλη μεριά, ισχυριζόμαστε ότι ο
πρώτος όρος του δεξιού σκέλους της ισότητας αυτής απαριθμεί το πλήθος όλων των διαμερισμών του
[n] σε k υποσύνολα, στην περίπτωση που το στοιχείο n σχηματίζει από μόνο του ένα υποσύνολο.
Πράγματι, όταν συμβαίνει αυτό, τα υπόλοιπα n − 1 στοιχεία του [n] πρέπει να διαμερισθούν σε k − 1
υποσύνολα και, εξ ορισμού, υπάρχουν S(n − 1, k − 1) τέτοιοι διαμερισμοί. Επομένως, ο δεύτερος όρος
του δεξιού σκέλους της παραπάνω ισότητας θα απαριθμεί το πλήθος όλων των διαμερισμών του [n]
σε k υποσύνολα, όταν το στοιχείο n δεν εμφανίζεται από μόνο του σε κανένα υποσύνολο. Επειδή,
καθώς τότε τα υπόλοιπα n − 1 στοιχεία του [n] πρέπει να διαμερισθούν σε k υποσύνολα, υπάρχουν
S(n − 1, k) τέτοιοι διαμερισμοί, για κάθε μια τοποθέτηση του n σε ένα από τα k υποσύνολα. ´Αρα
τότε, από τον κανόνα του γινομένου, βρίσκουμε k · S(n − 1, k) διαμερισμούς, που είναι ο δεύτερος όρος
του δεξιού σκέλους της ισότητας. Συνεπώς, ο κανόνας του αθροίσματος, συνεπάγεται ότι και το δεξιό
σκέλος της ισότητας απαριθμεί το πλήθος όλων των διαμερισμών του [n] σε k υποσύνολα.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-69-320.jpg)
![Ισχυρισμός: Η τοποθέτηση n διακριτών μπαλλών μέσα σε k
διακριτά κουτιά μπορεί να γίνει με k! · S(n,k) τρόπους.
Πράγματι, μπορούμε πρώτα να διαμερίσουμε το [n] σε k
διακριτά υποσύνολα με S(n,k) τρόπους και μετά να
ξεχωρίσουμε (να ταυτοποιήσουμε) τα k υποσύνολα, π.χ.,
βάζοντάς τα τις ετικέτες 1,2,...,k, κάτι που μπορεί να γίνει
με k! τρόπους, οπότε ο κανόνας του γινομένου συνεπάγεται
τον ισχυρισμό.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-70-320.jpg)
![Πόρισμα 42
Για κάθε θετικούς ακέραιους k ≤ n, το πλήθος όλων των
απεικονίσεων επί f: [n] −→ [k] είναι k! · S(n,k).
Απόδειξη: Επειδή, για κάθε j ∈ [k], το f−1(j) είναι ένα μη κενό υποσύνολο του [n], ουσιαστικά,
θέλουμε να βρούμε πώς μοιράζονται n διακριτές μπάλλες (τα στοιχεία του [n]) μέσα σε k διακριτά
κουτιά (τα στοιχεία του [k]). Αυτό, σύμφωνα με τον προηγούμενο ισχυρισμό, γίνεται με k! · S(n, k)
τρόπους.
Πόρισμα 43
Για κάθε θετικούς ακέραιους x και n,
xn =
n
k=0
S(n,k)(x)k.
Απόδειξη: Το αριστερό σκέλος είναι, προφανώς, το πλήθος των απεικονίσεων από το [n] στο [x].
Ισχυριζόμαστε ότι και το δεξιό σκέλος απαριθμεί το ίδιο, αλλά σύμφωνα με το μεγεθος των εικόνων.
Πράγματι, αν η πληθικότητα της εικόνας μιας τέτοιας απεικόνισης είναι k, τότε υπάρχουν x
k
επιλογές για να συμβεί αυτό. Επιπλέον όμως, το Πόρισμα 42 συνεπάγεται ότι υπάρχουν k! · S(n, k)
τέτοιες απεικονίσεις και, καθώς (x)k = k! · x
k , η απόδειξη ολοκληρώνεται.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-71-320.jpg)
![Ορισμός 44
Για κάθε θετικό ακέραιο n, συμβολίζουμε με B(n) το
πλήθος των διαμερισμών του [n] σε οποιασδήποτε
πληθικότητας (μη κενά) υποσύνολα και ονομάζουμε τα
B(n) αριθμούς Bell. Επιπλέον, θέτουμε B(0) = 1, ενώ,
προφανώς, ισχύει
B(n) =
n
i=0
S(n,i).
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-72-320.jpg)
![Θεώρημα 45
Για κάθε μη αρνητικό ακέραιο n,
B(n + 1) =
n
i=0
n
i
B(i).
Απόδειξη: Ουσιαστικά, πρέπει να αποδείξουμε ότι το άθροισμα του δεξιού
σκέλους απαριθμεί όλους τους διαμερισμούς του [n + 1]. Ας υποθέσουμε
λοιπόν ότι το στοιχείο n + 1 ανήκει σε κάποιο υποσύνολο πληθικότητας
n − i + 1, για κάποιο i = 0,1,...,n. Τότε, αφενός, υπάρχουν n
n−i = n
i
τρόποι, για να επιλεγούν τα στοιχεία που ανήκουν στο ίδιο υποσύνολο με
το στοιχείο n + 1, και, αφετέρου, υπάρχουν B(i) τρόποι, για να
διαμερισθούν τα υπόλοιπα i στοιχεία του [n + 1], οπότε αποδεικνύεται η
ζητούμενη σχέση.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-73-320.jpg)
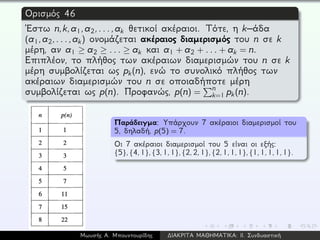
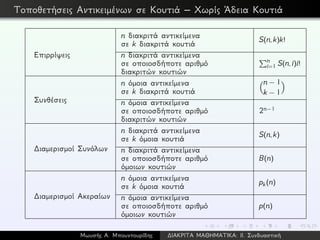





![Θεώρημα 47 (Η Αρχή του Εγκλεισμού–Αποκλεισμού)
´Εστω A1,A2,...,An πεπερασμένα σύνολα. Τότε
|A1 ∪A2 ∪...∪An| =
n
j=1
(−1)j−1
(i1,i2,...,ij) ⊆ [n]
|Ai1 ∩Ai2 ∩...∩Aij |.
Απόδειξη:14 Πρώτα, θα αποδείξουμε τον εξής ισχυρισμό: κάθε στοιχείο του
συνόλου A1 ∪ A2 ∪ ... ∪ An μετράται ακριβώς μια φορά από το δεξιό σκέλος
της προς απόδειξη σχέσης. Για να το δείξουμε αυτό, ας πάρουμε ένα
x ∈ A1 ∪ A2 ∪ ... ∪ An κι ένα αυθαίρετο σύνολο δεικτών S ⊆ [n] τέτοιο ώστε
x ∈ Ai αν και μόνον αν i ∈ S. ´Εστω s = |S|, το οποίο θα πρέπει να είναι
s ≥ 1. Καθώς το x ∈ Ai μόνο εφόσον i ∈ S, οι μόνες t–άδες (i1,i2,...,it) ⊆ [n]
τέτοιες ώστε x ∈ Ai1 ∩ Ai2 ∩ ... ∩ Ait είναι αυτές, για τις οποίες
14
Η Αρχή του Εγκλεισμού–Αποκλεισμού μερικές φορές ονομάζεται Τύπος του Κόσκινου (Sieve
Formula).
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-81-320.jpg)

![Παράδειγμα: Σε έναν γάμο έχουν προσκληθεί 30 άτομα, τα οποία πρέπει
να χωρισθούν σε 3 ομάδες, η κάθε μια των 10 ατόμων, για να καθίσουν σε
3 τραπέζια. ´Ομως, υπαρχουν 4 άτομα, οι a,b,c,d, τέτοιοι ώστε ο a δεν
θέλει να καθίσει στο ίδιο τραπέζι με τον b και ο c με τον d. Με πόσους
τρόπους τότε μπορούν να χωρσθούν τα 30 άτομα σε 3 ομάδες;
´Εστω [30] το σύνολο των 30 ατόμων, των οποίων η ταυτοποίηση έχει γίνει έτσι ώστε οι a, b, c, d να
αντιστοιχούν στα 4 πρώτα στοιχεία του [30], δηλαδή, στα 1, 2, 3, 4, αντιστοίχως.
´Εστω A το σύνολο των ανεπιθύμητων διαμερισμών του [30] σε 3 μέρη (ομάδες), που είναι τέτοιοι
ώστε τα 1 και 2 να περιέχονται στην ίδια ομάδα, και έστω B το σύνολο των ανεπιθύμητων
διαμερισμών του [30] σε 3 μέρη, που είναι τέτοιοι ώστε τα 3 και 4 να περιέχονται στην ίδια ομάδα.
Και στις 2 περιπτώσεις, έχοντας τον περιορισμό 2 συγκεκριμένα στοιχεία να συνυπάρχουν στην ίδια
ομάδα, βρίσκουμε ότι |A| = |B| = 28!
10!10!8!2 , όπου το έξτρα 2 στον παρανομαστή οφείλεται στο
γεγονός ότι δεν έχει σημασία με ποια διάταξη τα 2 συνυπάρχοντα στοιχεία εμφανίζονται σε μια
ομάδα.
Στη συνέχεια, ας υπολογίσουμε το |A ∩ B|. Προφανώς, το A ∩ B είναι το σύνολο των διαμερισμών
του [30] σε 3 ομάδες, όταν τα 1, 2, 3 και 4 είτε όλα βρίσκονται στην ίδια ομάδα ή ανά δυο (τα 1
και 2 και τα 3 και 4) βρίσκονται σε δυο ομάδες από τις 3. Η πρώτη περίπτωση μπορεί να γίνει
26!
10!10!6!2 φορές, ενώ η δεύτερη περίπτωση 26!
10!8!8!2 φορές, δηλαδή, σύμφωνα με τον κανόνα του
αθροίσματος, |A ∩ B| = 26!
10!10!6!2 + 2 26!
10!8!8!2 = 26!
10!10!6!2 + 26!
10!8!8!
, γιατί υπάρχουν 2 τρόποι που τα
2 σύνολα {1, 2} και {3, 4} μπορούν να κατανεμηθούν σε 2 ομάδες.
Επομένως, το πλήθος των ανεπιθύμητων διαμερισμών του [30] σε 3 μέρη, που είναι τέτοιοι ώστε είτε
τα 1 και 2 ή τα 3 και 4 να περιέχονται στην ίδια ομάδα, είναι |A ∪ B| = |A| + |B| − |A ∩ B| =
28!
10!10!8!
− 26!
10!10!6!2 − 26!
10!8!8!
.
Τέλος, για να υπολογίσουμε το πλήθος των επιθυμητών διαμερισμών, χρησιμοποιούμε τον κανόνα της
διαφοράς, όπου πρέπει να αφαιρέσουμε το |A ∩ B| από το πλήθος όλων των δυνατών διαμερισμών
του [30] σε 3 μέρη, που είναι ίσο προς 30
10!10!10!3!
, όπου το έξτρα 3! στον παρανομαστή οφείλεται
στο γεγονός ότι δεν λαμβάνουμε υπόψη την μεταξύ τους διάταξη των 3 μερών. Επομένως, το
πλήθος των επιθυμητών διαμερισμών είναι 30
10!10!10!3!
− 28!
10!10!8!
+ 26!
10!10!6!2 + 26!
10!8!8!
.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-83-320.jpg)
![Παράδειγμα: 10 άτομα πρέπει να ομαδοποιηθούν, αλλά με έναν τέτοιο
τρόπο ώστε κάποια συγκεκριμένα 3 άτομα, οι a,b και c, να μην μπορούν
να σχηματίσουν ομάδες, στις οποίες θα είναι μόνα τους το καθένα από
αυτά τα 3 άτομα. Με πόσους τρόπους τότε μπορούν να χωρσθούν έτσι τα
30 άτομα;
´Εστω [10] το σύνολο των 10 ατόμων, των οποίων η ταυτοποίηση έχει γίνει έτσι ώστε οι a, b, c να
αντιστοιχούν στα 3 πρώτα στοιχεία του [10], δηλαδή, στα 1, 2, 3, αντιστοίχως. Προφανώς, τότε
θέλουμε να βρούμε το πλήθος των διαμερισμών του [10] εξαιρουμένων των διαμερισμών που
περιέχουν τα σύνολα {1}, {2}, {3} μεταξύ των μερών (ομάδων) τους. Θα κάνουμε αυτόν τον
υπολογισμό, ξεκινώντας από το πλήθος των ανεπιθύμητων διαμερισμών του [10], δηλαδή, αυτών
στους οποίους τουλάχιστον ένα από τα μέρη τους είναι το {1} ή το {2} ή το {3}. ´Εστω λοιπόν,
για κάθε i ∈ [3], Ai το σύνολο των διαμερισμών του [10], ένας από τους οποίους περιέχει το
μονοσύνολο {i}. Προφανώς τότε, θέλουμε να βρούμε το μέγεθος της ένωσης A1 ∪ A2 ∪ A3 και η αρχή
του εγκλεισμού–αποκλεισμού μας λέει ότι |A1 ∪ A2 ∪ A3| = |A1| + |A2| + |A3| − |A1 ∩ A2|
−|A1 ∩ A3| − |A2 ∩ A3| + |A1 ∩ A2 ∩ A3|.
Πρώτα, παρατηρούμε ότι το σύνολο A1 όλων των διαμερισμών του [10], που περιέχουν το
μονοσύνολο {1} ως ένα από τα μέρη τους, έχει πληθικότητα |A1| = B(9). ´Αρα, παρόμοια,
|A2| = |A3| = B(9).
Στη συνέχεια, ισχυριζόμαστε ότι το σύνολο A1 ∩ A2 των διαμερισμών του [10], που περιέχουν τα
μονοσύνολα {1} και {2} ως δυο από τα μέρη τους, έχει πληθικότητα |A1 ∩ A2| = B(8). ´Αρα,
παρόμοια, |A1 ∩ A3| = |A2 ∩ A3| = B(8).
Τέλος, θα έχουμε ότι το σύνολο A1 ∩ A2 ∩ A3 των διαμερισμών του [10], που περιέχουν τα
μονοσύνολα {1}, {2} και {3} ως τρία από τα μέρη τους, έχει πληθικότητα |A1 ∩ A2 ∩ A3| = B(7).
Επομένως, συνολικά, |A1 ∪ A2 ∪ A3| = 3B(9) − 3B(8) + B(7) και χρησιμοποιώντας τον κανόνα της
διαφοράς, πρέπει να αφαιρέσουμε το |A1 ∪ A2 ∪ A3| από το πλήθος όλων των δυνατών διαμερισμών
του [10] (σε οποιοοδήποτε πλήθος μερών), που είναι ίσο προς B(10), οπότε βρίσκουμε ότι το πλήθος
των επιθυμητών διαμερισμών είναι B(10) − 3B(9) − 3B(8) − B(7).
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-84-320.jpg)

![4 ´Εστω m θετικός ακέραιος. Συμβολίζουμε με φ(m) το
πλήθος των ακέραιων στο [m] που είναι σχετικά
πρώτοι με το m. Αν p,q και r είναι τρεις διακριτοί
πρώτοι αριθμοί, υπολογίστε το φ(pqr).
5 ´Εστω Fk(n) το πλήθος των διαμερισμών του [n] σε
k τμήματα, το κάθε ένα από τα οποία περιέχει
τουλάχιστον ένα στοιχείο. Εκφράστε τους αριθμούς
Fk(n) συναρτήσει του αριθμού Stirling δεύτερου
είδους.
6 Πόσοι τριψήφιοι θετικοί ακέραιοι είναι διαιρετοί με
τουλάχιστον έναν από τους αριθμούς 6 και 7;
7 Πόσοι διψήφιοι θετικοί ακέραιοι είναι σχετικά
πρώτοι και με τους δυο αριθμούς 2 και 3;
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-86-320.jpg)
![8 Με πόσους τρόπους μπορούμε να διατάξουμε τους
αριθμούς του συνόλου {1,1,2,2,3,4,5} έτσι ώστε
καθε δυο διαδοχικοί αριθμοί να μην είναι ίδιοι;
9 Πόσοι πίνακες 2 × 2 υπάρχουν, των οποίων τα
στοιχεία είναι από το σύνολο {0,1,...,k} και οι
οποίοι δεν περιέχουν καμία σειρά και καμία στήλη
με μόνο μηδενικά στοιχεία;
10 ´Εστω F(n) το πλήθος των διαμερισμών του [n] σε
τμήματα, το κάθε ένα από τα οποία περιέχει
τουλάχιστον δυο στοιχεία. Εκφράστε τους αριθμούς
F(n) συναρτήσει των αριθμών Bell.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-87-320.jpg)


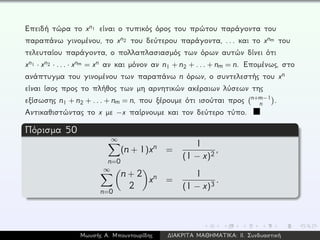





![Θεώρημα 52 (Ο Τύπος του Γινομένου)
´Εστω δυο διαφορετικές διαδικασίες (τρόποι) απαρίθμη-
σης, n ένας μη αρνητικός ακέραιος και an,bn δυο απαριθ-
μήσεις των στοιχείων του [n], η κάθε μια σύμφωνα με μια
από τις διαδικασίες αυτές. ´Εστω cn το πλήθος των τρό-
πων για να διαμερισθεί το [n] σε δυο (ενδεχομένως κενά)
υποσύνολα S = {1,2,...,i},T = {i + 1,i + 2,...,n} τέτοια
ώστε, το κάθε ένα από τα οποία να απαριθμείται σύμ-
φωνα με μια από τις εν λόγω διαδικασίες. Αν A(x),B(x),
C(x) είναι οι γεννήτριες συναρτήσεις των ακολουθιών
{an},{bn},{cn} (αντιστοίχως), τότε A(x)B(x) = C(x).
Απόδειξη: Εξ υποθέσεως, υπάρχουν ai τρόποι απαρίθμησης των στοιχείων του S και bn−i τρόποι
απαρίθμησης των στοιχείων του T. Αυτό ισχύει, για κάθε i, εφόσον 0 ≤ i ≤ n. Επομένως,
cn = n
i=0 aibn−i και το αποτέλεσμα απορρέει από το προηγούμενο Λήμμα.
Ο Τύπος του Γινομένου ισχύει για γινόμενα οποιουδήποτε πεπερασμένου
πλήθους όρων.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-97-320.jpg)




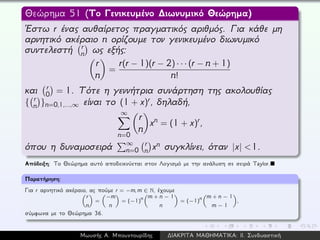
![Εκθετικές Γεννήτριες Συναρτήσεις
Ορισμός 53
´Εστω {an}n=0,1,...,∞ μια ακολουθία πραγματικών
αριθμών. Τότε η τυπική δυναμοσειρά E(x) = E(an; x) =
∞
n=0 an
xn
n! ονομάζεται εκθετική γεννήτρια συνάρτηση
της ακολουθίας {an}n=0,1,...,∞.
Στοιχειώδη Παραδείγματα:
Αν an = 1, για κάθε n ≥ 0, τότε E(1; x) = ∞
n=0
xn
n!
= ex.
Αν an = an, για κάποιο a ∈ R και για κάθε n ≥ 0, τότε
E(an; x) = ∞
n=0
(ax)n
n!
= eax. Ως ειδική περίπτωση, αν an = 2n, που
είναι το πλήθος των υποσυνόλων του [n], τότε
E(2n; x) = ∞
n=0
(2x)n
n!
= e2x.
Αν an = n!, που είναι το πλήθος των μεταθέσεων του [n], τότε
E(n!; x) = ∞
n=0 n! xn
n!
= 1
1−x .
Αν an = (m)n = m!
(m−n)!
, που είναι το πλήθος των n–μεταθέσεων του [m],
τότε E((m)n; x) = ∞
n=0(m)n
xn
n!
= m
n=0
m
n xn = (1 + x)m.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-102-320.jpg)



![Θεώρημα 54 (Ο Τύπος του Γινομένου για Εκθετικές
Γεννήτριες Συναρτήσεις)
´Εστω δυο διαφορετικές διαδικασίες (τρόποι) απαρίθμη- σης,
n ένας μη αρνητικός ακέραιος και an,bn δυο απαριθ- μήσεις
των στοιχείων του [n], η κάθε μια σύμφωνα με μια από τις
διαδικασίες αυτές. ´Εστω cn το πλήθος των τρό- πων για να
διαμερισθεί το [n] σε δυο (ενδεχομένως κενά) υποσύνολα
S = {1,2,...,i},T = {i + 1,i + 2,...,n} τέτοια ώστε, το κάθε
ένα από τα οποία να απαριθμείται σύμ- φωνα με μια από τις
εν λόγω διαδικασίες. Αν A(x),B(x), C(x) είναι οι εκθετικές
γεννήτριες συναρτήσεις των ακολουθιών {an},{bn},{cn}
(αντιστοίχως), τότε A(x)B(x) = C(x).
Απόδειξη: Ξέρουμε ότι υπάρχουν n
i τρόποι επιλογής των στοιχείων ενός υποσυνόλου του [n] με i
στοιχεία. Εξ υποθέσεως, υπάρχουν ai τρόποι απαρίθμησης των στοιχείων του S και bn−i τρόποι
απαρίθμησης των στοιχείων του T. Αυτό ισχύει, για κάθε i, εφόσον 0 ≤ i ≤ n. Επομένως,
cn = n
i=0
n
i aibn−i και το αποτέλεσμα απορρέει από το προηγούμενο Λήμμα.
Ο Τύπος του Γινομένου ισχύει για γινόμενα οποιουδήποτε πεπερασμένου
πλήθους όρων.
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-106-320.jpg)




![7 ´Εστω an το πλήθος των τρόπων που μπορούμε να
χαλάσουμε n ευρώ σε χαρτονομίσματα των 10 και
των 5 ευρώ και σε κέρματα του 1 ευρώ.
Υπολογίστε τη σύνηθη γεννήτρια συνάρτηση A(x)
της ακολουθίας an.
8 Υπολογίστε τη σύνηθη γεννήτρια συνάρτηση της
ακολουθίας an = n2.
9 ´Εστω f(n) το πλήθος των υποσυνόλων του [n], στα
οποία η απόσταση μεταξύ οποιωνδήποτε δυο
στοιχείων είναι τουλάχιστον 3. Υπολογίστε τη
σύνηθη γεννήτρια συνάρτηση της f(n).
10 ∆ιαιρούμε μια ομάδα ατόμων σε τρεις υπο–ομάδες
A,B και C και ζητούμε κάθε υπο–ομάδα να
στοιχισθεί σε σειρά. Επίσης απαιτούμε την
υπο–ομάδα A να περιέχει περιττό πλήθος ατόμων
και την B άρτιο. Με πόσους τρόπους μπορεί αυτό
να γίνει;
Μωυσής Α. Μπουντουρίδης ∆ΙΑΚΡΙΤΑ ΜΑΘΗΜΑΤΙΚΑ: ΙΙ. Συνδυαστική](https://image.slidesharecdn.com/2-140519111249-phpapp01/85/I-111-320.jpg)
