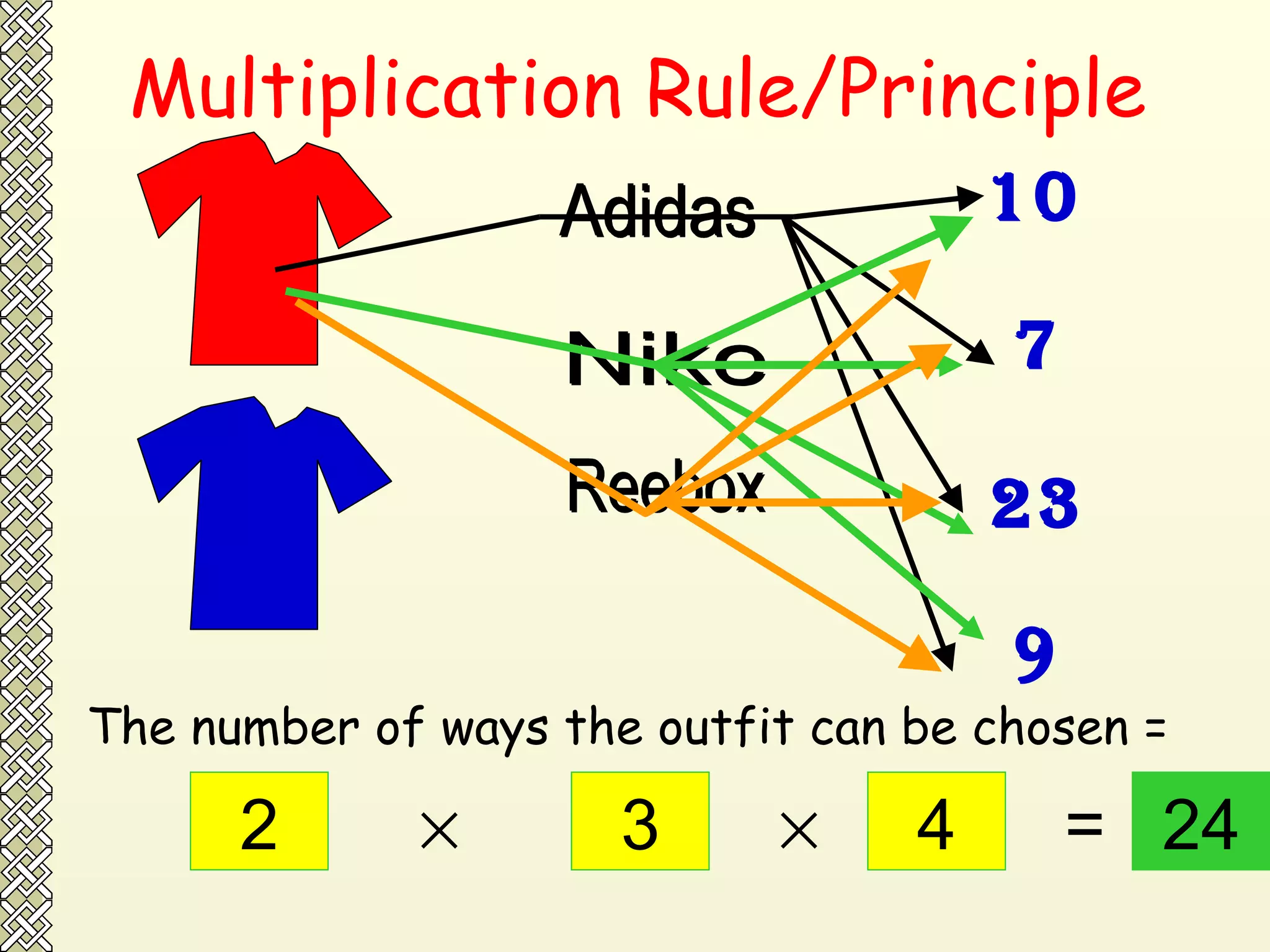
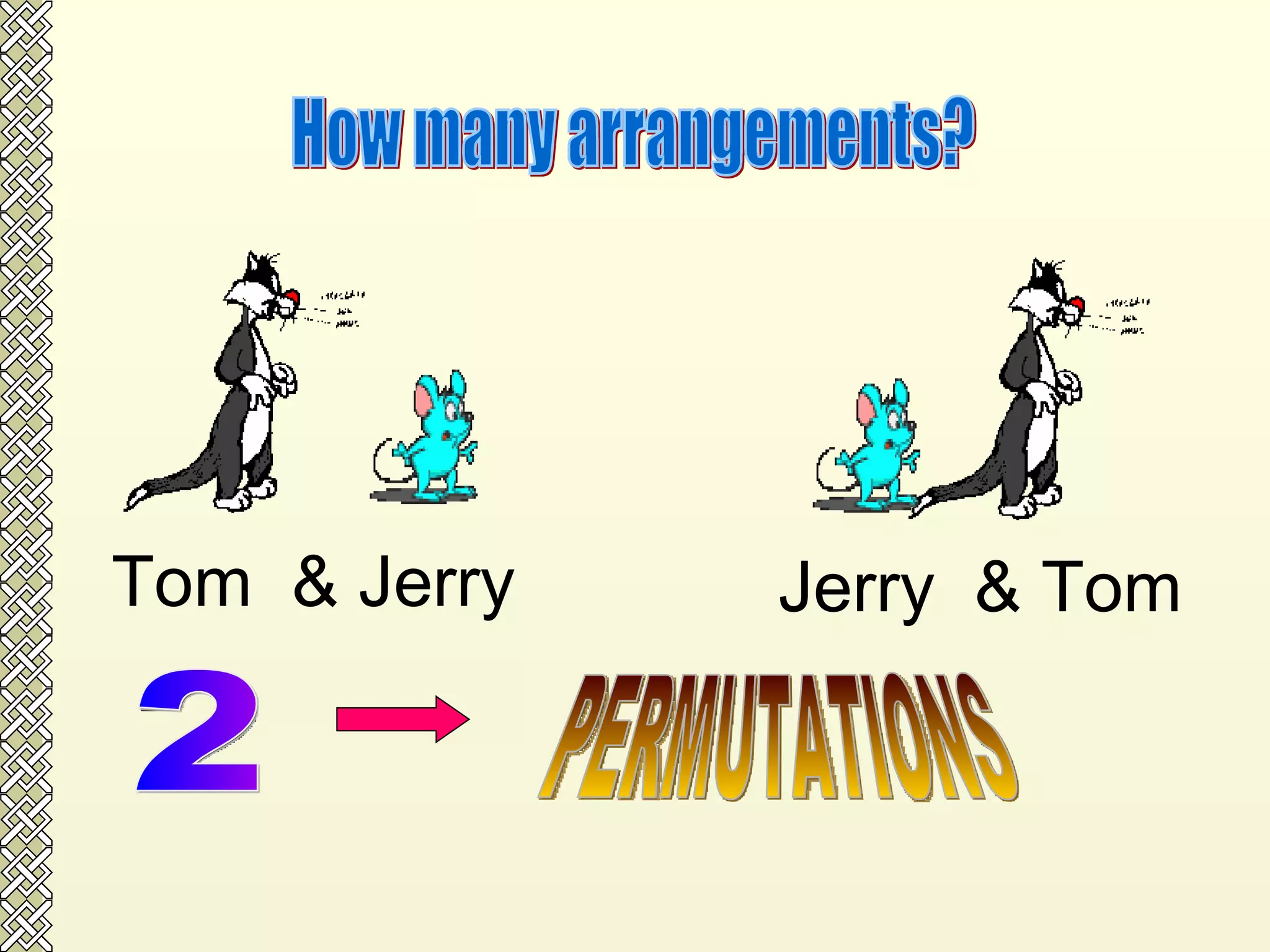
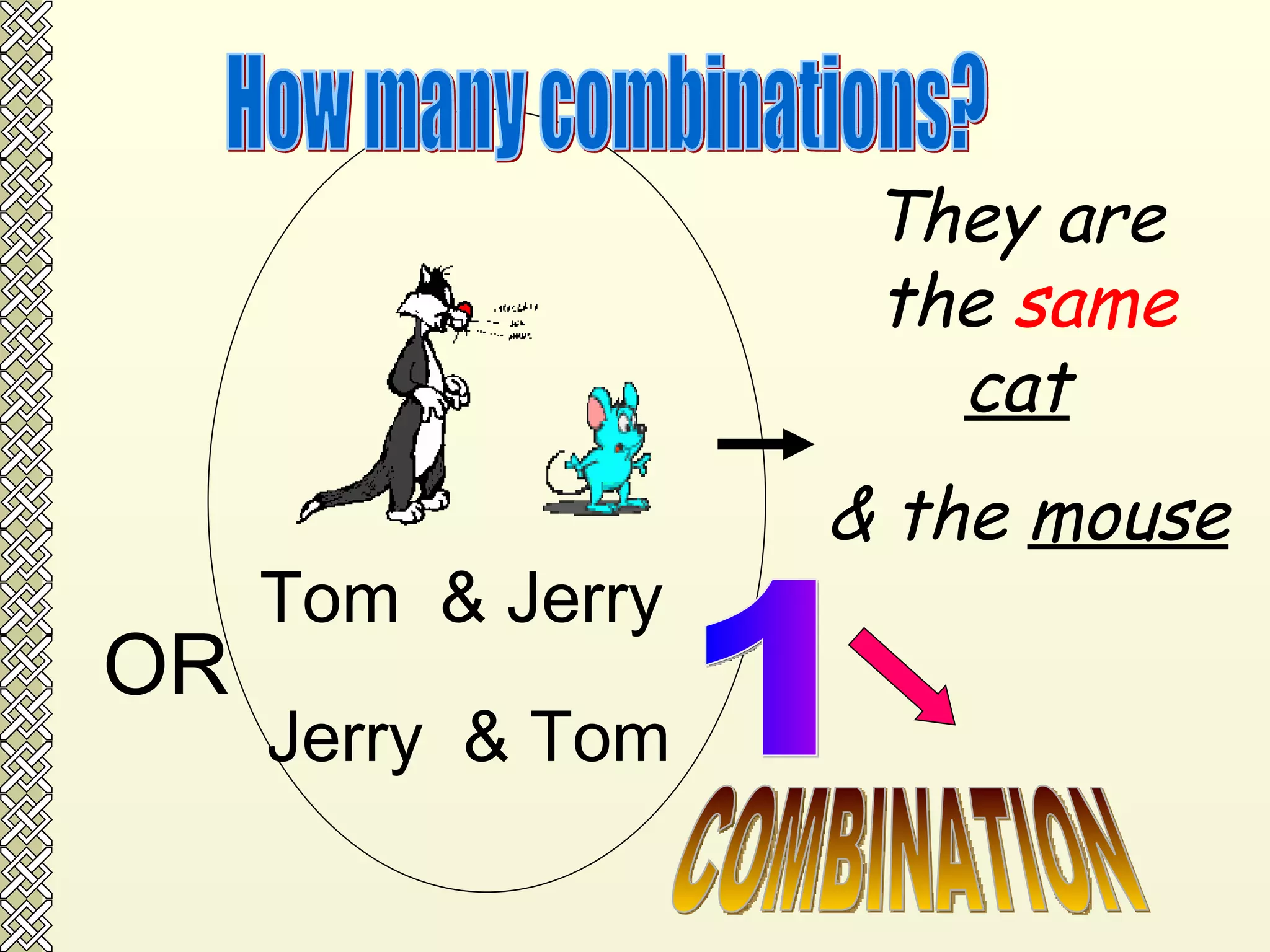
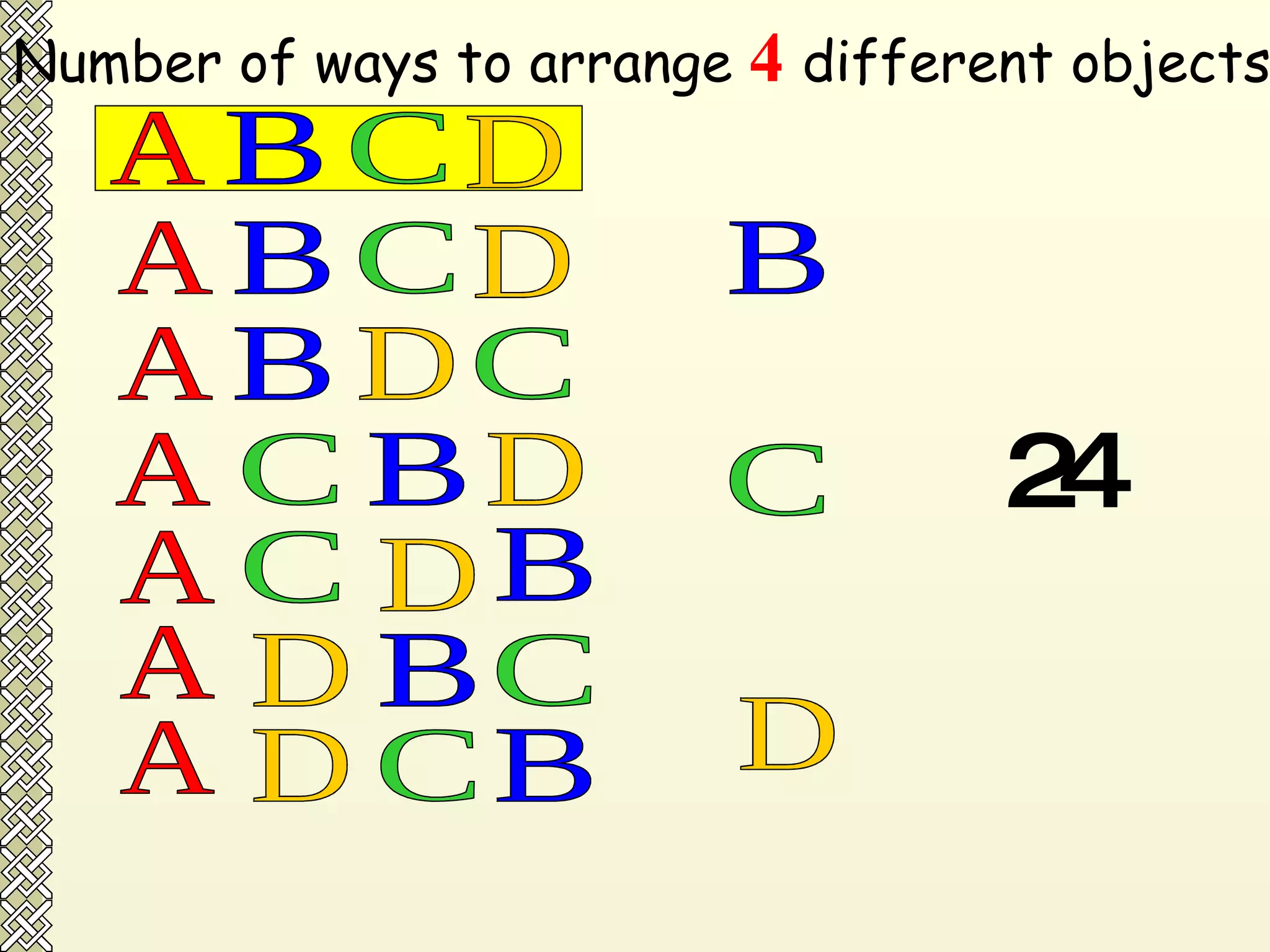
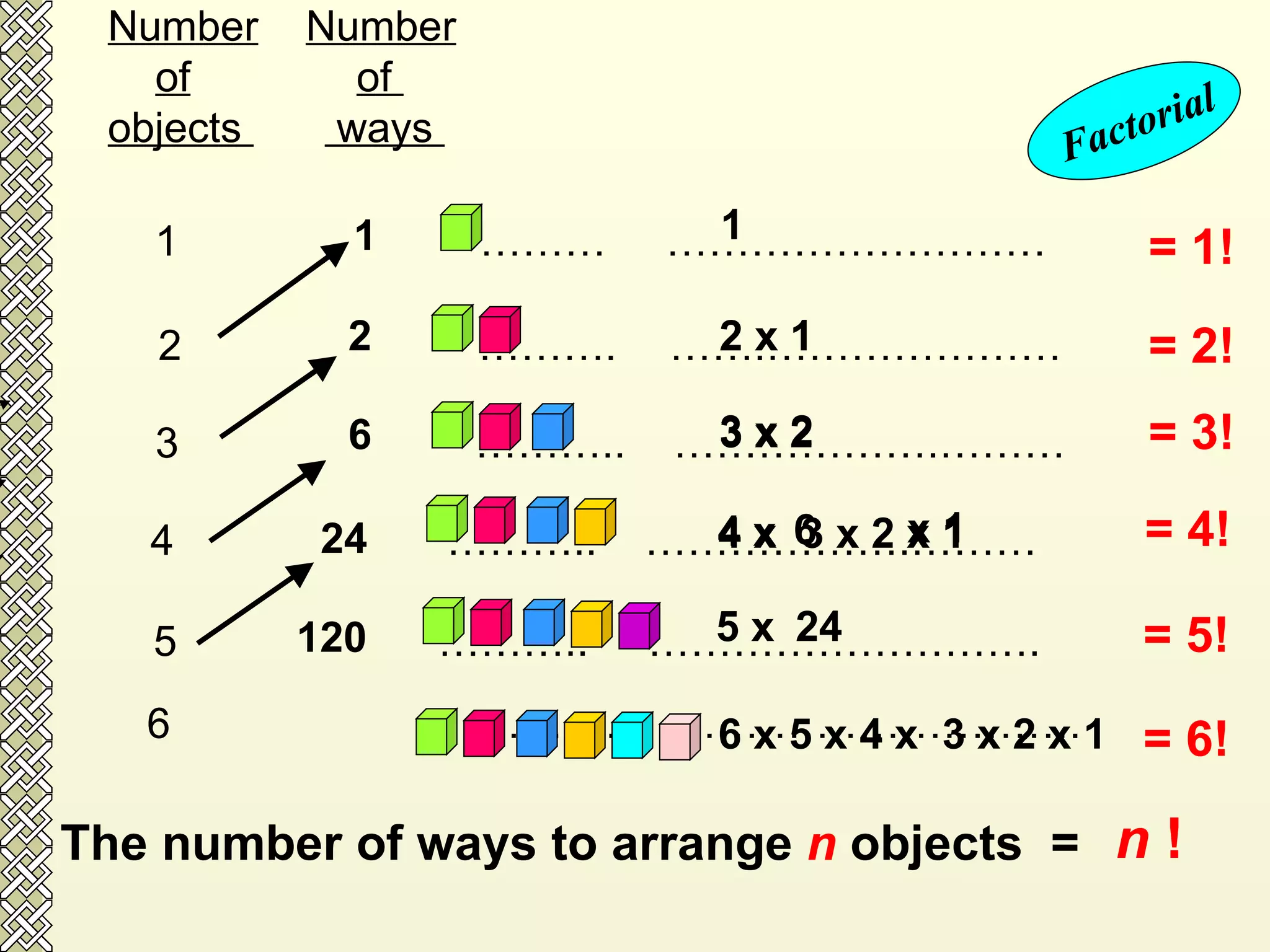
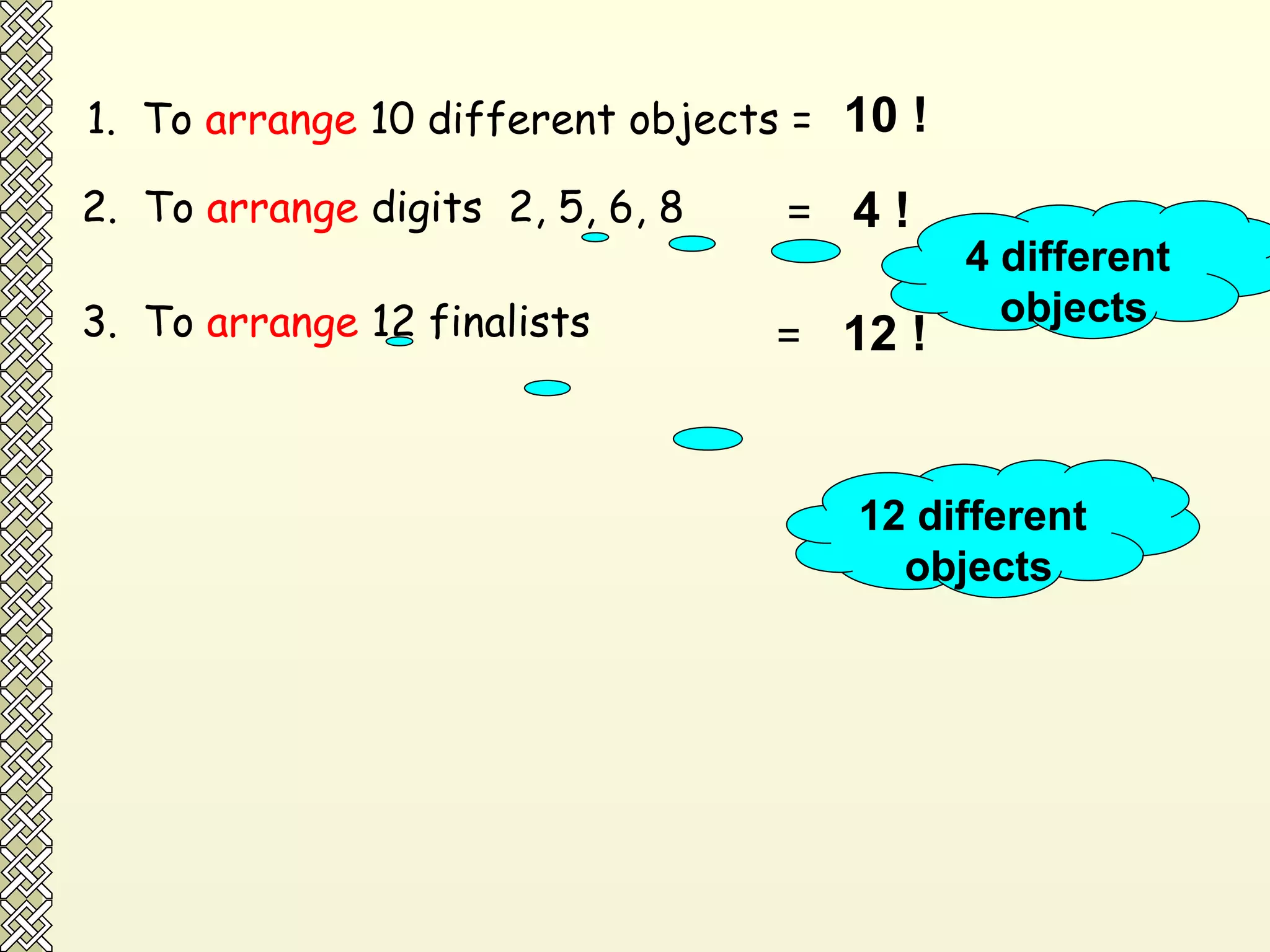
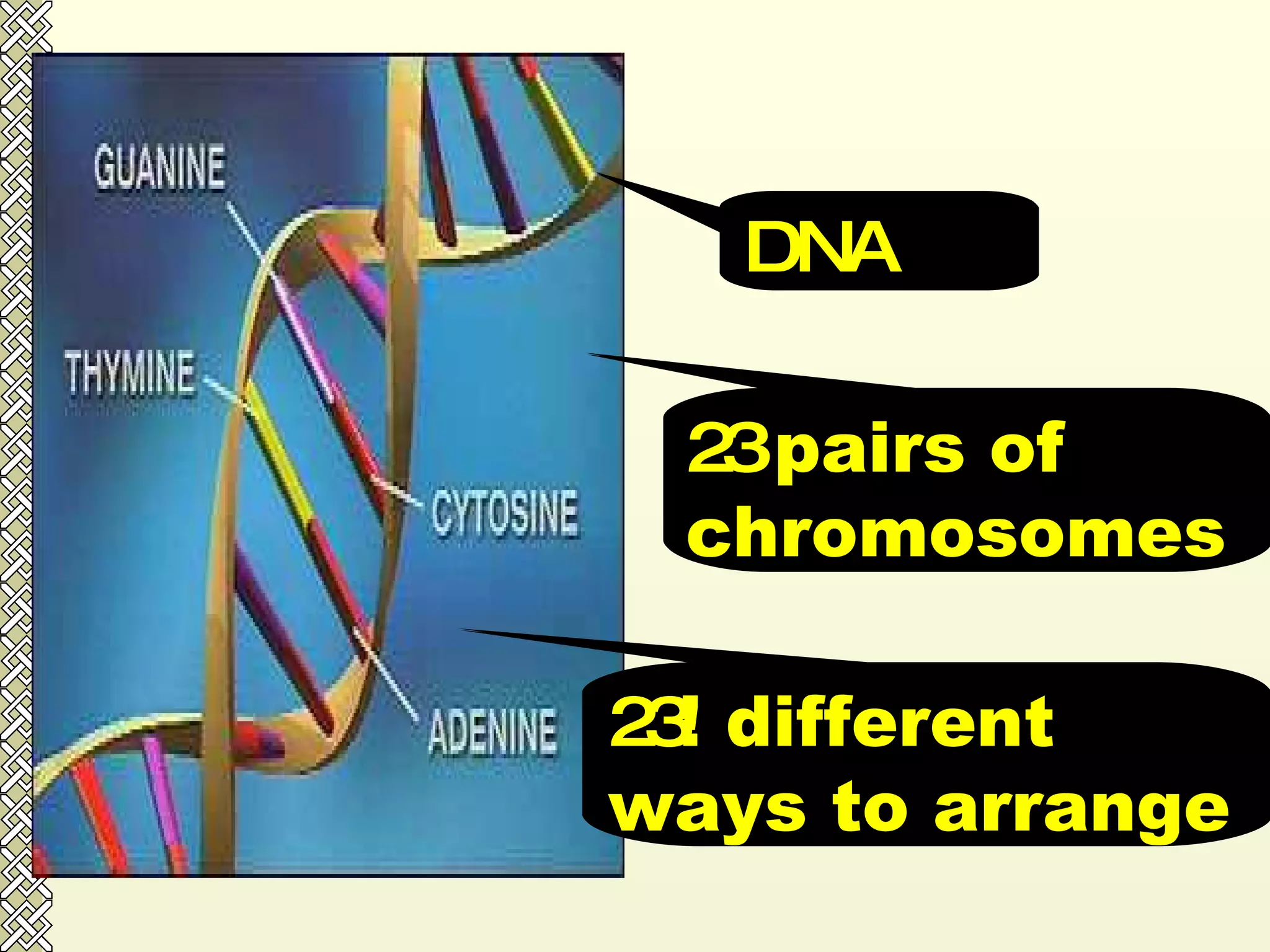
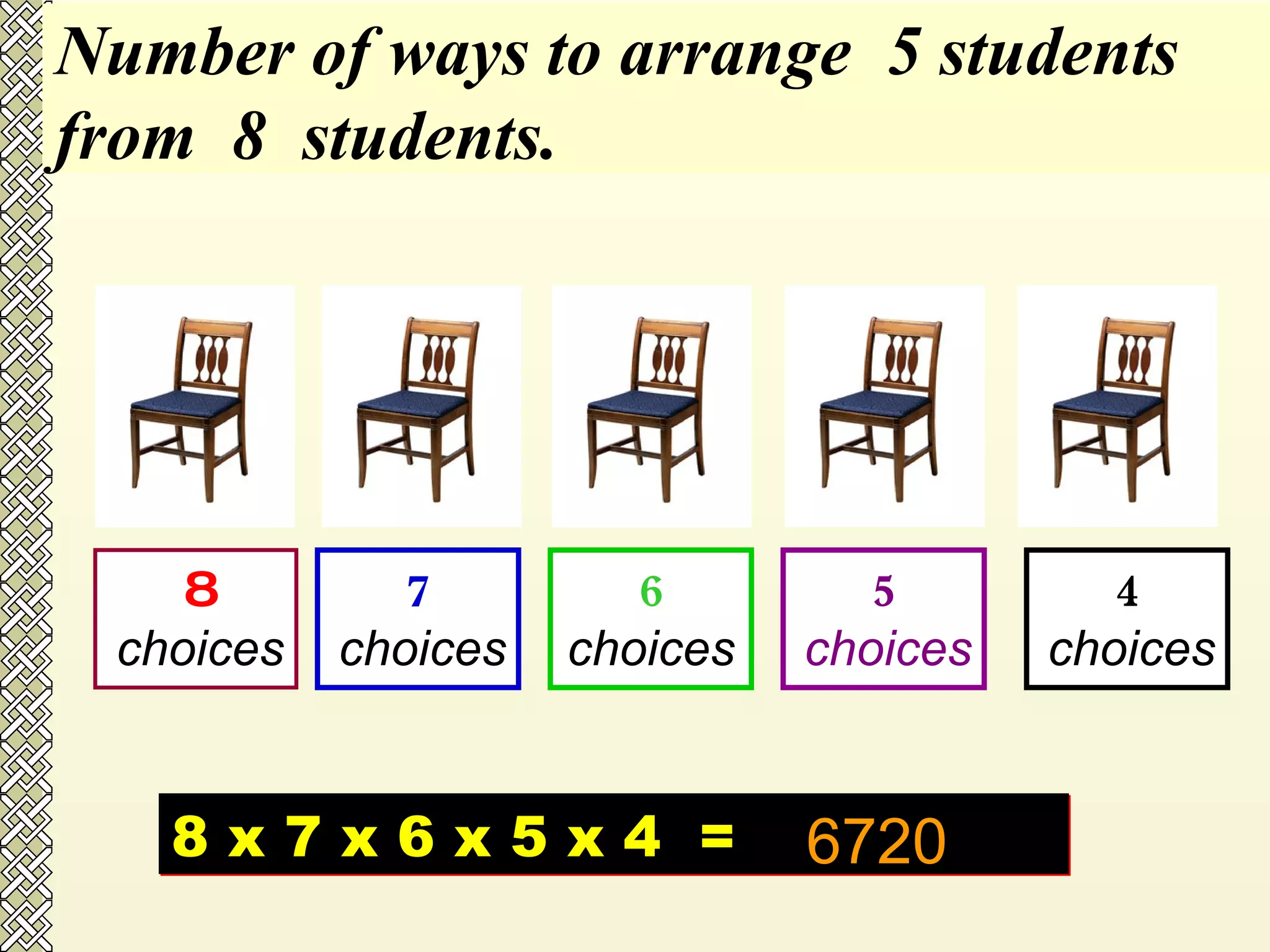
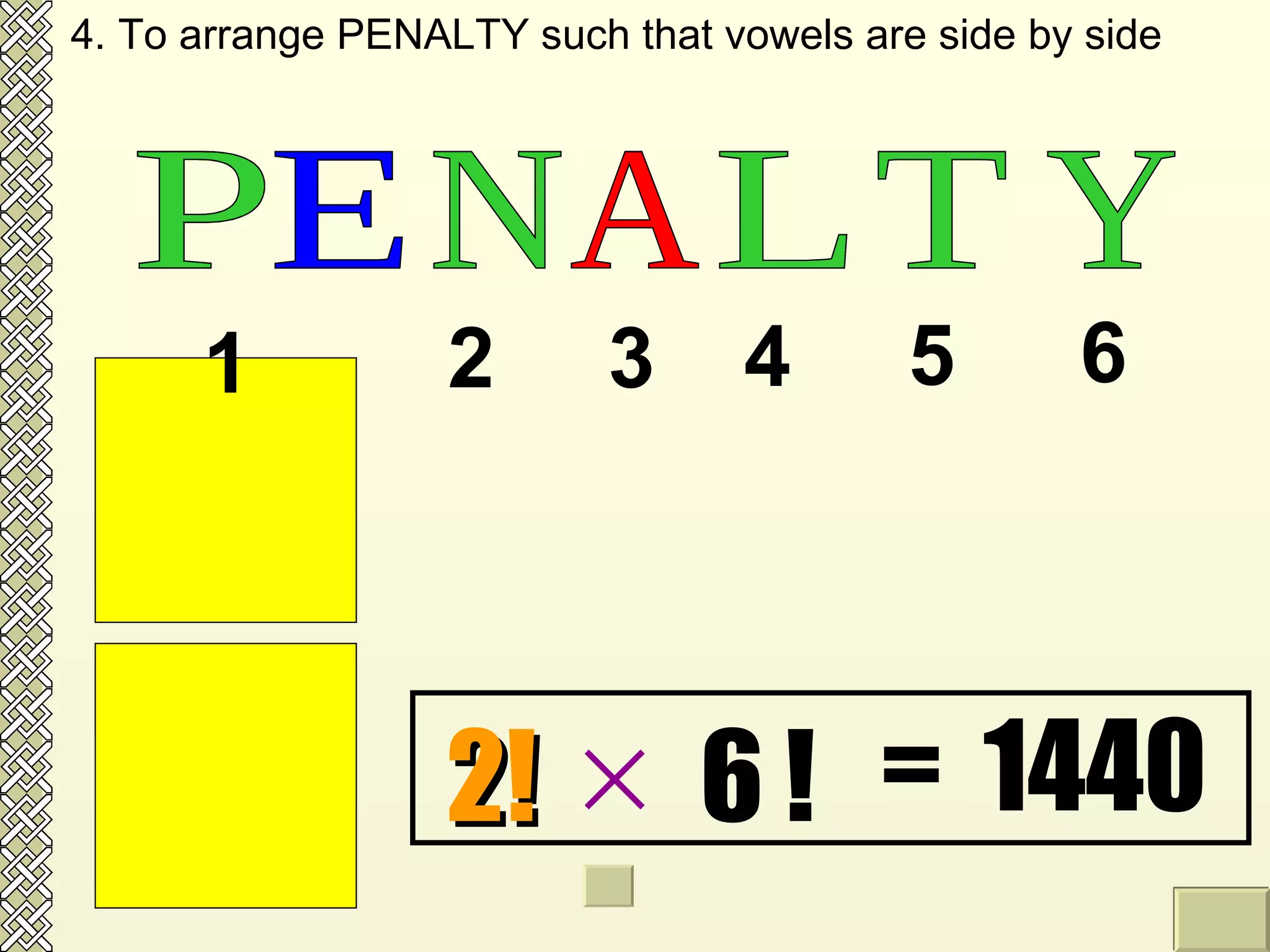
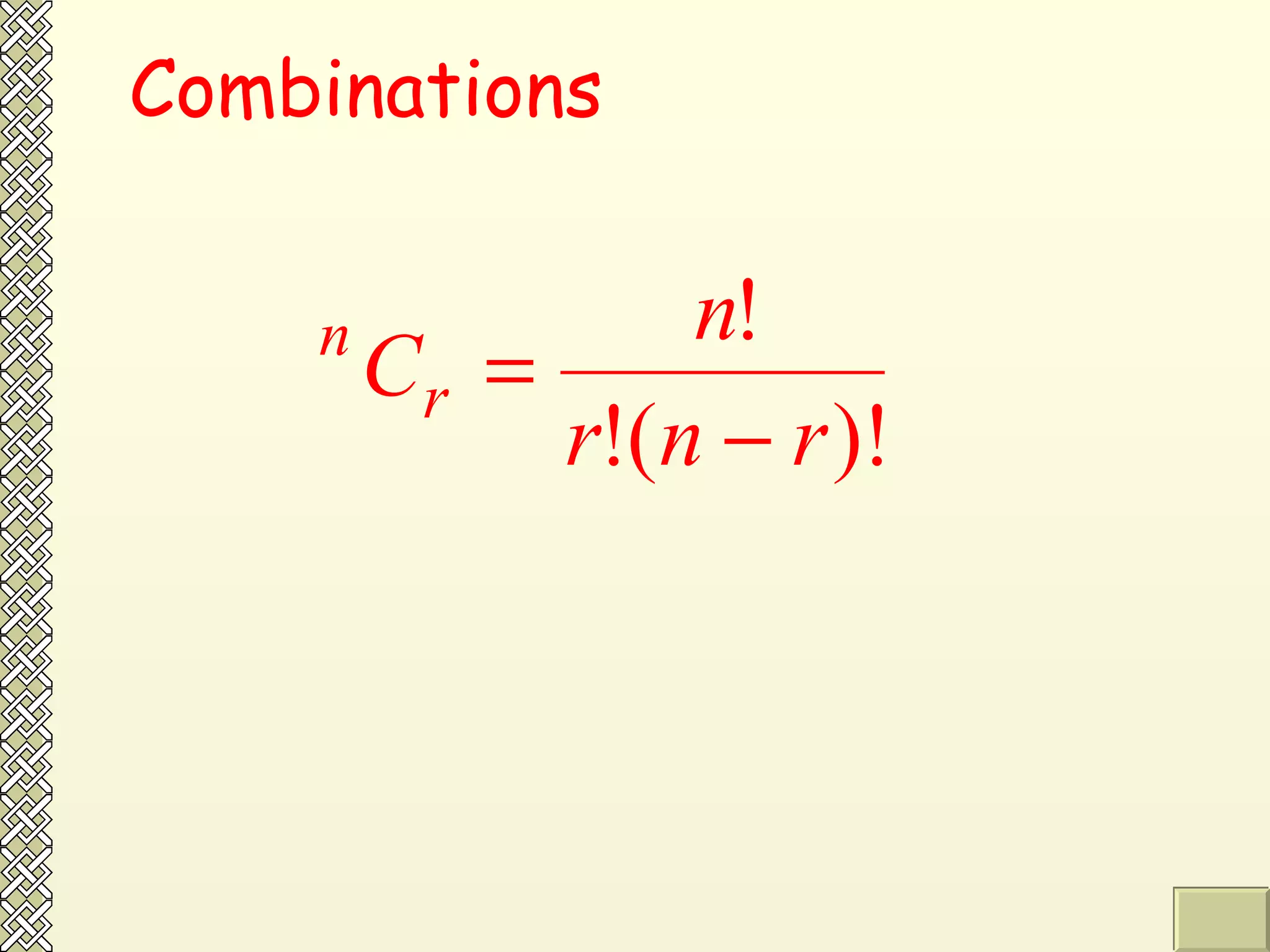The document discusses permutations and combinations. It defines permutations as arrangements where order is important, and combinations as groupings where order is not important. It provides examples of calculating permutations and combinations using factorial notation and formulas. The differences between permutations and combinations are outlined. Conditions that can be applied, such as objects being together or separated, are also discussed along with how to handle them in calculations.

1. PERMUTATION & COMBINATION

2. MULTIPLICATION RULE If an operation can be performed in r different ways and a second operation can be performed in s different ways, then both the operations can be performed successively in r x s ways.

3. Multiplication Rule/Principle Adidas Reebox Nike 10 23 7 9 2 3 4   24 = The number of ways the outfit can be chosen =

4. PERMUTATION In permutation, the order of the objects or outcomes is important. Each different order represents a different outcome. Permutation – variation, order Arrangement

5. PERMUTATION Permutation – the arrangement is important How many ways can the letter X and Y be arranged? X Y X Y There are two ways  two different permutation

6. COMBINATIONS In Combinations, we do not arrange the selections in order. Combination – grouping,selection Choices

7. Combination Arrangement is not important X Y Or X Y Are the same  one combination

8. Tom & Jerry Jerry & Tom How many arrangements? 2 PERMUTATIONS

9. Tom & Jerry Jerry & Tom They are the same cat & the mouse OR How many combinations? 1 COMBINATION

10. DIFFERENCES BETWEEN PERMUTATIONS AND COMBINATIONS PERMUTATIONS COMBINATIONS Arranging people, digits, numbers, alphabets, letters, colours. Keywords: Arrangements, arrange,… Selection of menu, food, clothes, subjects, teams. Keywords: Select, choice,…

11. Permutation Number of ways to arrange n different objects

12. Number of ways to arrange 3 different objects A B C A B C B B A C C A C A B C B A 6 ways A B C

13. Number of ways to arrange 4 different objects A B C D B C D 24 A B C D A B C D A B C D A B C D A B C D A B C D

14. Number Number of of objects ways 1 ……… ……………………… 2 ………. …….………………… 3 ……….. ……………….……… 4 ……….. ……………….……… 1 2 x 1 1 2 6 3 x 2 2 x 1 24 4 x 6 3 x 2 x 1 120 5 x 24 4 x 3 x 2 x 1 6 x 5 x 4 x 3 x 2 x 1 = 6! = 5! = 4! = 3! = 2! = 1! The number of ways to arrange n objects = n ! 5 ……….. ………………………. 6 ……….. ………………………. Factorial

15. 1. To arrange 10 different objects = 10 ! 2. To arrange digits 2, 5, 6, 8 = 4 ! 4 different objects 3. To arrange 12 finalists 12 different objects = 12 !

16. DNA 23 pairs of chromosomes 23 ! different ways to arrange

17. The number of ways to arrange 23 different objects ? 25852016738884976640000 23 ! = 2.6 x 10 22

18. Permutation Number of ways to arrange r objects from n objects

19. 8 choices 7 choices 6 choices 5 choices 4 choices Number of ways to arrange 5 students from 8 students. 8 x 7 x 6 x 5 x 4 = 6720

20. 8 choices 7 choices 6 choices 5 choices 4 choices number of ways to arrange r from n objects n (n-1) (n-2) (n-3) (n-(r-1))

21. 1. Questions related to Forming Numbers with digits and conditions Use Multiplication Rules

22. Condition 1 Find the number of ways to form 5 letter word from the letters W, O,R, L, D, C, U, P with the condition that it must starts with a vowels. is filled first W R L D C P O O U 2 7 6 5 4 U =1680

23. Find the number of ways to form 6 letter word from the letters B, E, C, K, H, A, M with the condition that it must starts with a consonant. B CKHM 5 EA 6 5 5x6x5x4x3x2 = 1200 4 3 2

24. 2. Questions related to Forming Numbers with digits and conditions Use Multiplication Rules Conditions : Sit side by side , next to each other – group together and consider as 1 object for arranging with other objects, make sure remember the arrangement of the grouped objects itself.

25. A E A E P N L T Y P N L T Y A E 6 ! 2! = 1440 4. To arrange PENALTY such that vowels are side by side 1 2 3 4 5 6 

26. 3. Complimentary Methods Use: The number of arrangements of event A = Total arrangements – arrangement of A’ A A’ S

27. Example Find the number of the arrangement of all nine letters of word SELECTION in which the two letters E are not next to each other. Solutions: Total no. of arrangements – No. of arrangements with two E next to each other

28. Combinations n objects choose n = 1

29. N = 4 Choose 1: A B C D A B C D Choose 2: A B A C A D B C Choose 3: A B C A C D B C D B D C D A B D Choose 4: A B C D = 4 = 4 C 1 = 6 = 4 C 2 = 4 = 4 C 3 = 1 = 4 C 4

30. Combinations

32. Conditional Combination 1 A football team has 17 local players and 3 imported players. Eleven main players are to be chosen with the condition that it must consist of 2 imported players. Find the number of ways the main player can be chosen. import local 3 17 2 9 3 C 2 17 C 9   = 72930 r n

33. Condition Combination 2 A committee consisting of 6 members is to be chosen from 3 men and 4 women. Find the number of ways at least 3 women are chosen. W3 M3 , or W4 M2 , 4 C 3 X 3 C 3 + 4 C 4 X 3 C 2 = 7

34. CONCLUSIONS 1. Compare and Contrast between Permutations and Combinations.

35. DIFFERENCES BETWEEN PERMUTATIONS AND COMBINATIONS PERMUTATIONS COMBINATIONS 1. Order is importent 2. Arranging people, digits, numbers, alphabets, letters, colours, … 3. Keywords: Arrangements, arrange,… Order is not important. 2. Selection of menu, food, clothes, subjects, teams, … Keywords: Select, choice,…

36. 2. Formula Difference between the two formulae: Use the calculator to find the values of permutations and combinations.

37. 3. If not sure, try to use the Multiplication Rules Know the ways how to handle conditions like: Sit side by side , next to each other, even/odd numbers, more/less than, starts/ends with vowel/consonants, …

38. Find the number of ways to form 6 letter word from the letters B, E, C, K, H, A, M with the condition that it must starts with a consonant. B CKHM 5 EA 6 5 5x6x5x4x3x2 = 1200 4 3 2

39. 4. For complicated cases: Simplify by using Complimentary Methods The number of arrangements of event A = Total arrangements – arrangement of A’ A A’ S

40. PROBABILITY