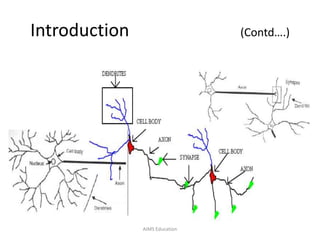
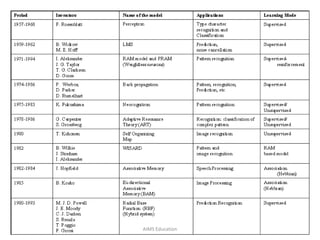
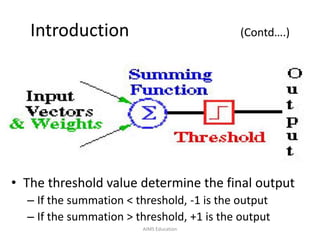
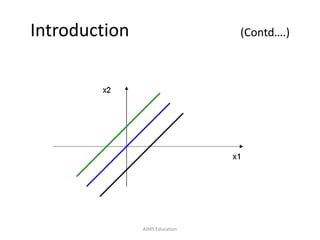
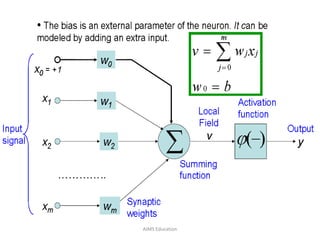
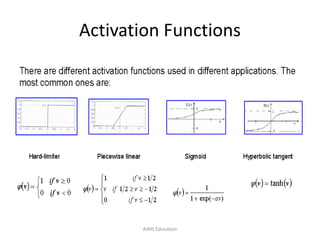
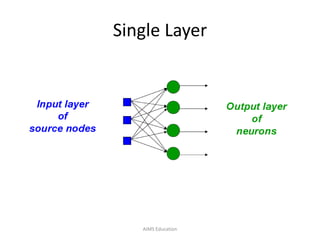
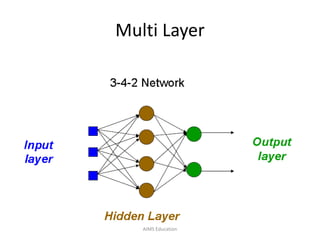
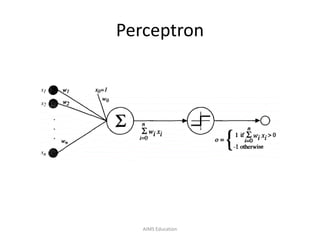
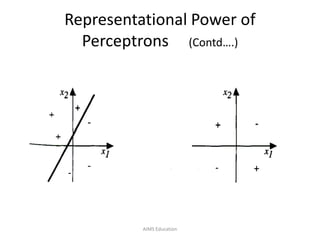
The document provides an overview of artificial neural networks (ANNs), detailing their structure, design, and applications in pattern recognition and data classification. It discusses the basic components of ANNs such as neurons, activation functions, and the training process, emphasizing the importance of weights and learning methods like the perceptron and delta rule. Additionally, it highlights suitable problems for neural network learning, indicating their robustness to noise and the challenges posed by the interpretability of learned models.

1. ARTIFICIAL NEURAL NETWORKS
AIMS Education

2. Introduction
• Simple computational elements forming a large
network
– Emphasis on learning (pattern recognition)
– Local computation (neurons)
• Configured for a particular application
– Pattern recognition/data classification
• ANN algorithm
– Modeled after brain
• Brain: 100,000 times slower response
– Complex tasks (image, sound recognition, motion con)
– –10,000,000,000 times efficient in energy
consumption/op
AIMS Education

3. Introduction (Contd….)
• Artificial Intelligence
• Structure
– Inputs vs Dendrites
– Weights vs Synaptic gap
– Neurons vs Soma
– Output vs Axon
AIMS Education

4. Introduction (Contd….)
AIMS Education

5. History

6. AIMS Education

7. Definition
A neural network is a massively parallel
distributed processor made up of simple
processing units, which has a natural tendency
for storing experiential knowledge and making
it available for use
AIMS Education

8. Introduction (Contd….)
• The threshold value determine the final output
– If the summation < threshold, -1 is the output
– If the summation > threshold, +1 is the output
AIMS Education

9. Introduction (Contd….)
• The neuron is the basic information
processing unit of an ANN.
• It consists of:
– A set of links, describing the neuron inputs, with
weightsW1, W2, …, Wm
– An adder function (linear combiner) for computing
the weighted sum of the inputs (real numbers):
AIMS Education

10. Introduction (Contd….)
– Activation function(squashing function) for
limiting the amplitude of the neuron output.
• The bias b has the effect of applying an affine
transformation to the weighted sum u
v = u + b
AIMS Education

11. Introduction (Contd….)
AIMS Education

12. AIMS Education

13. Activation Functions
AIMS Education

14. Designing an ANN
• Designing an ANN consist of
– Arranging neurons in various layers
– Deciding the type of connections among neurons for
different layers, as well as among the neurons within a
layer
– Deciding the way a neuron receives input and
produces output
• Determining the strength of connection within
the network by allowing the network learn the
appropriate values of connection weights by
using a training data set.
• The process of designing a neural network is an
iterative process
AIMS Education

15. Designing an ANN (Contd….)
• Layers
– Single layer: Input and output layer
• No computation at the input layer
• Computation takes place at the output layer
– Multi layer: Input, hidden(s) and output layers
• Computations are done at the hidden(s) and the output layer
• Connection
– Fully connected
• Each neuron on the first layer is connected to every neuron on
the second layer
– Partially connected
• A neuron of the first layer does not have to be connected to all
neurons on the second layer
AIMS Education

16. Designing an ANN (Contd….)
• Very complex webs of interconnected neurons
– Simple interconnected units in ANNs
• Each unit takes in a number of real-valued
inputs
– Possibly outputs of other units
• Produces a single real-valued output
– May become the input to many other units
AIMS Education

17. Single Layer
AIMS Education

18. Multi Layer
AIMS Education

19. Appropriate problems for Neural
Network Learning
• Instances are represented by many attribute-
value pairs
– The target function to be learned is defined over
instances that can be described by a vector of
predefined features
– Input attributes may be highly correlated or
independent of one another
– Input values can be any real values
AIMS Education

20. Appropriate problems for Neural
Network Learning (Contd….)
• The target function output may be discrete-
valued, real-valued, or a vector of several real- or
discrete-valued attributes
• Training examples may contain errors
– Robust to noisy data
• Long training times are acceptable
– Network training algorithms typically require longer
training times
– Depends on factors such as
• The number of weights in the network
• The number of training examples considered
AIMS Education

21. Appropriate problems for Neural
Network Learning (Contd….)
• Fast evaluation of the learned target function
may be required
– Learning times are relatively long, evaluating the
learned network, in order to apply it to a
subsequent instances, is typically very fast
• The ability of humans to understand the
learned target function is not important
– Weights learned are often difficult for humans to
interpret
AIMS Education

22. Perceptron
AIMS Education

23. Perceptron (Contd….)
• Takes a vector of real-valued inputs
• Calculates a linear combination of these
inputs
• Outputs a 1 if the result is greater than some
threshold
• Outputs a -1 otherwise
• Weights: An information that allows ANN to
achieve the desired results. This information
changes during the learning process
AIMS Education

24. Perceptron (Contd….)
• Given inputs 𝑥1 through 𝑥𝑛, the output 𝑜(𝑥
1,…,n𝑛) computed by the perceptron is
𝑜(𝑥1,…,𝑥𝑛)= 1 𝑖𝑓
𝑤0+ 𝑤1𝑥1+ 𝑤2𝑥2+ …+ 𝑤𝑛𝑥𝑛 > 0
−1 other𝑤𝑖𝑠𝑒
• Where each 𝑤𝑖 is a real-valued constant, or
weight, that determines the contribution of
input 𝑥𝑖 to the perceptron output
AIMS Education

25. Perceptron (Contd….)
• An additional constant input 𝑥0=1, allowing us
to write the inequality as
∑i=1 to n 𝑤𝑖𝑥𝑖>0
In vector form as 𝑤.𝑥 > 0
• For brevity, we will sometimes write the
perceptron function as 𝑜(𝑥) =𝑠𝑔𝑛(𝑤.𝑥) where
𝑠𝑔𝑛(𝑦)= 1 𝑖𝑓 𝑦 > 0
-1 otherwise
AIMS Education

26. Representational Power of
Perceptrons
• A perceptron can be seen as representing a
hyper plane decision surface in the 𝑛-
dimensional space of instances (i.e., points)
• It outputs a 1 for instances lying on one side of
the hyper place
• Outputs a −1 for instances lying on the other
side
AIMS Education

27. Representational Power of
Perceptrons (Contd….)
AIMS Education

28. Representational Power of
Perceptrons (Contd….)
• The equation for the decision surface is 𝑤.𝑥 =0
• Some sets of positive and negative examples
cannot be separated by any hyperplace
• The ones that can be separated are called
linearly separable sets of examples
AIMS Education

29. Perceptron Training Rule
• How to learn the weights for a single perceptron?
• The task is to learn a weight vector that causes
the perceptron to produce the correct ±1 output
for each of the given training examples
• Perceptron rule and delta rule algorithms
– Provide the basis for learning networks of many units
AIMS Education

30. Perceptron Training Rule (Contd….)
• One way to learn an acceptable weight vector is to
– Begin with random weights
– Iteratively apply the perceptron to each training
example
– Modify the perceptron weights whenever it
misclassifies an example
– The process is repeated
• Iterating through the training examples as many times
as needed
• Until the perceptron classifies all training examples
correctly
AIMS Education

31. Perceptron Training Rule (Contd….)
• Weights are modified at each step according to the
perceptron training rule
• Here 𝑡 is the target output for the current training example
• 𝑜 is the output generated by the perceptron
• 𝜂 is a positive constant called the learning rate
– Moderates the degree to which weights are changed at each
step
– Usually set to some small value (e.g., 0.1)
– Sometimes made to decay as the number of weight-tuning
iterations increases
AIMS Education

32. Perceptron Training Rule (Contd….)
• Why should it converge to successful weight
values?
– Suppose the training example is correctly classified
already by the perceptron
– In this case 𝑡 −𝑜 is zero
– Makes Δ𝑤𝑖 zero
– No weights are updated
– Suppose it outputs a -1 when the target output is +1
– Weights must be altered to increase the value of (𝑤.𝑥)
• For example, if 𝑥𝑖>0, then increasing 𝑤𝑖 will bring the
perceptron closer to correctly classifying in this example
• Can be shown to converge within a finite number of
applications of the perceptron training rule
AIMS Education

33. Gradient Descent and the Delta Rule
• Perceptron rule works fine when the training
examples are linearly separable
– Otherwise can fail to converge
• Delta rule is defined to overcome this hurdle
• If training examples are not linearly separable
• Delta rule converges to the best fit
approximation to the target concept
AIMS Education

34. Delta Rule (Contd….)
• Becomes the basis for learning interconnected
networks (multilayer network)
• Training an unthresholded perceptron, a linear
unit for which the output 𝑜 is given by
– 𝑜(𝑥) = (w.x)
– It corresponds to the first stage of a perceptron,
without the threshold
AIMS Education

35. Delta Rule (Contd….
• Training error (weight vector), relative to the
training examples
• Where 𝐷 is the set of training examples
• 𝑡𝑑 is the target output for the training example 𝑑
• 𝑜𝑑 is the output of the linear unit for training
example 𝑑
• is simply half the squared difference
between the target output 𝑡𝑑 and the linear unit
output 𝑜𝑑 summed over all training examples
AIMS Education