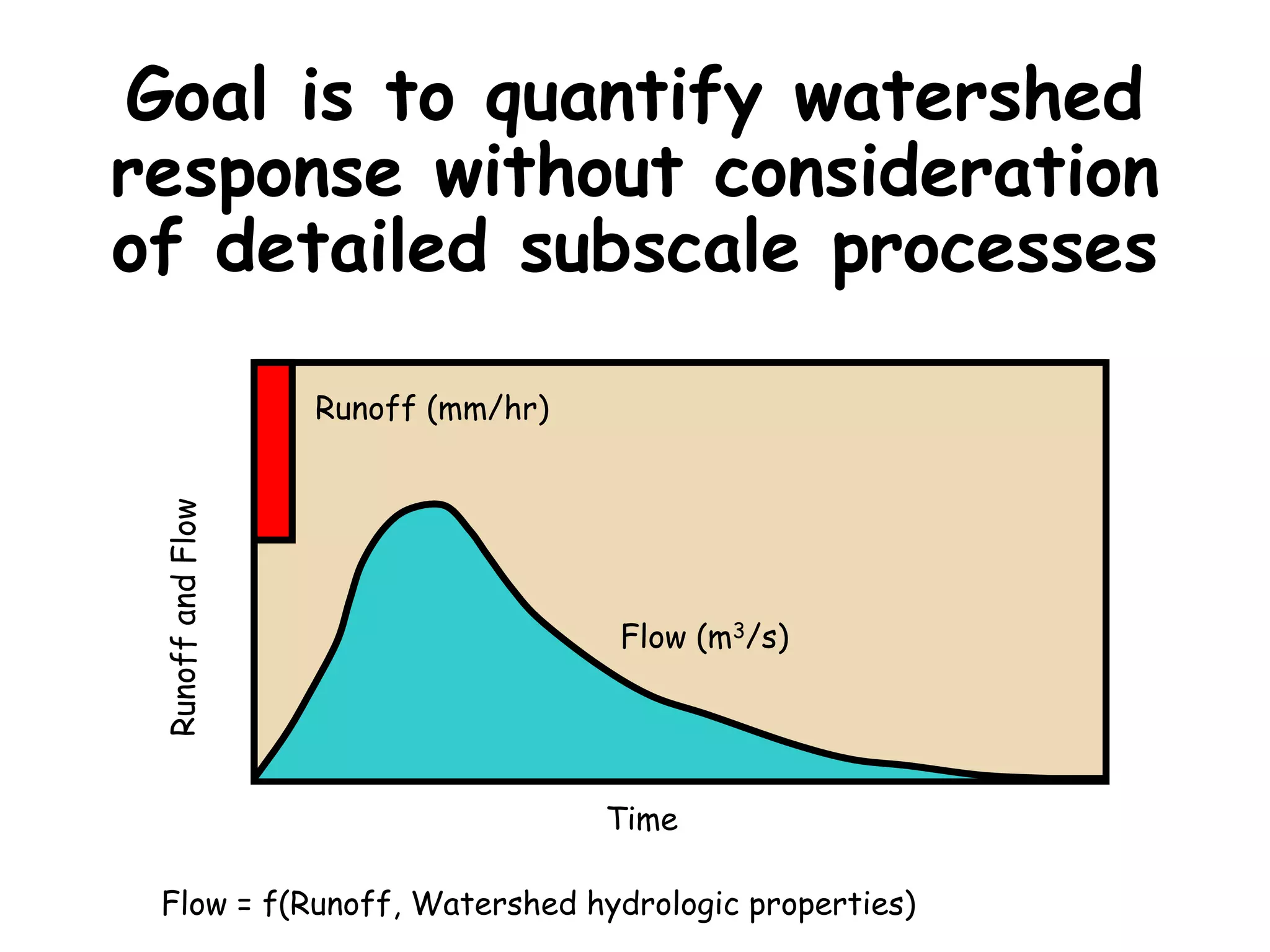
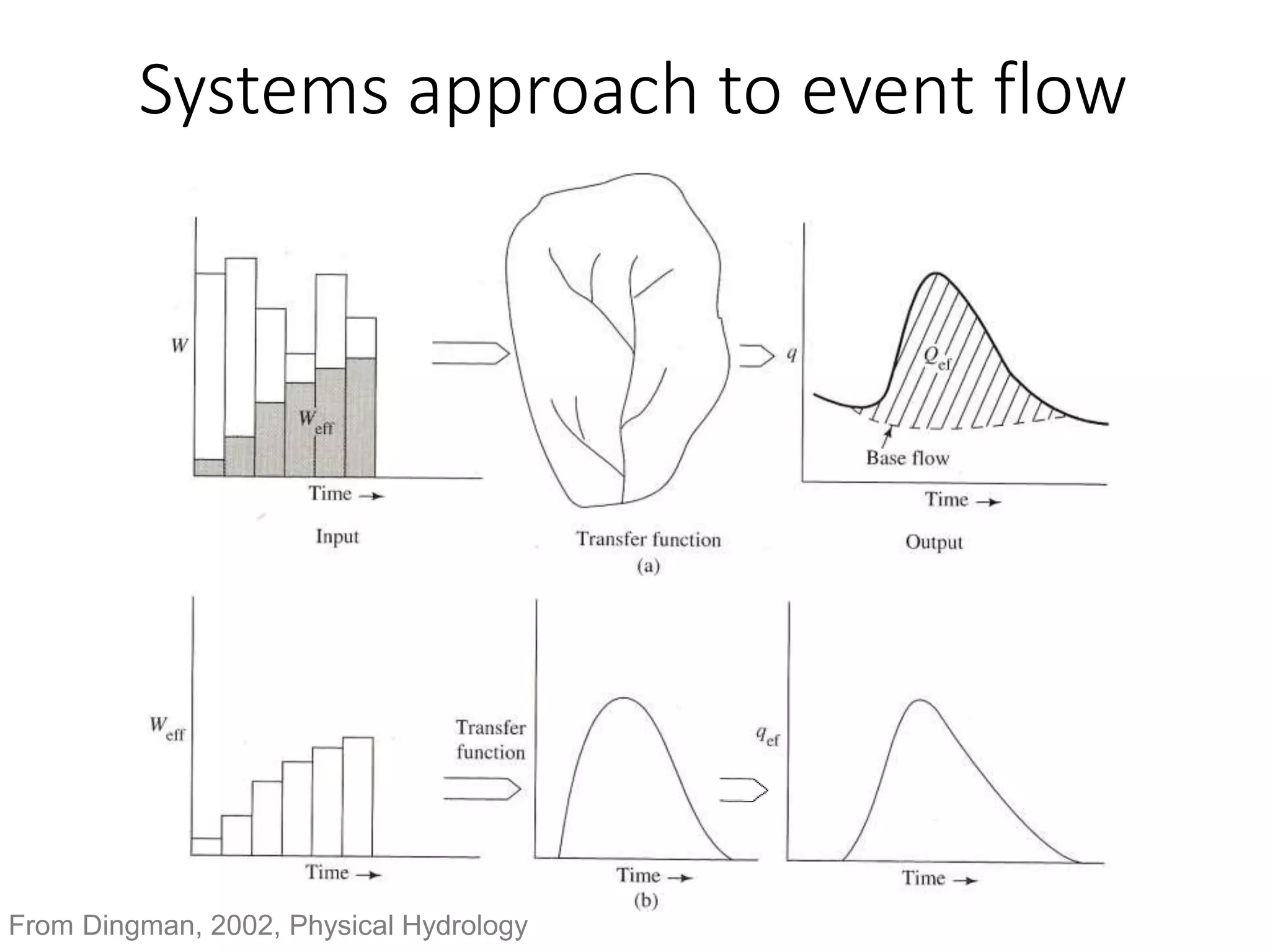
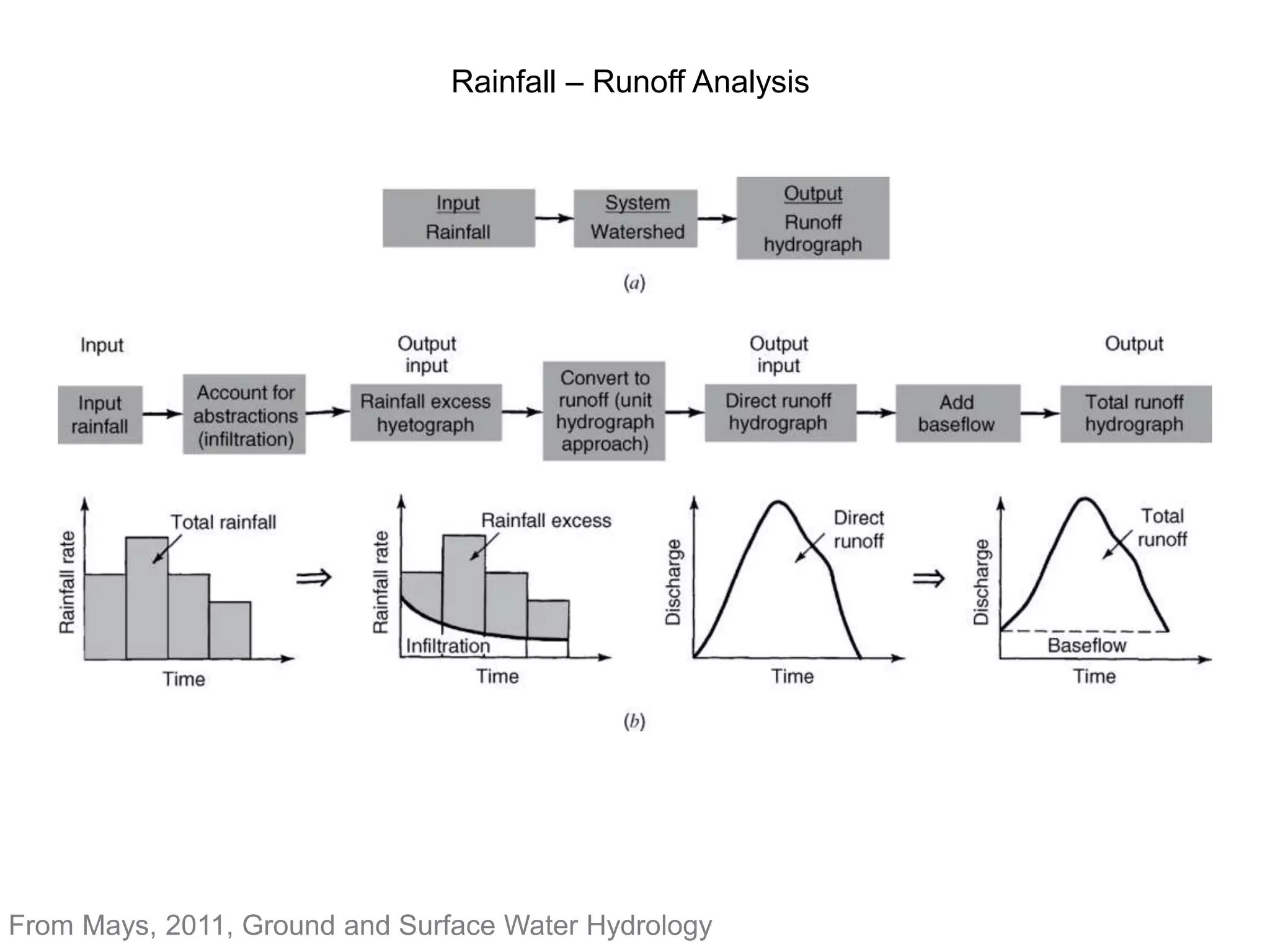
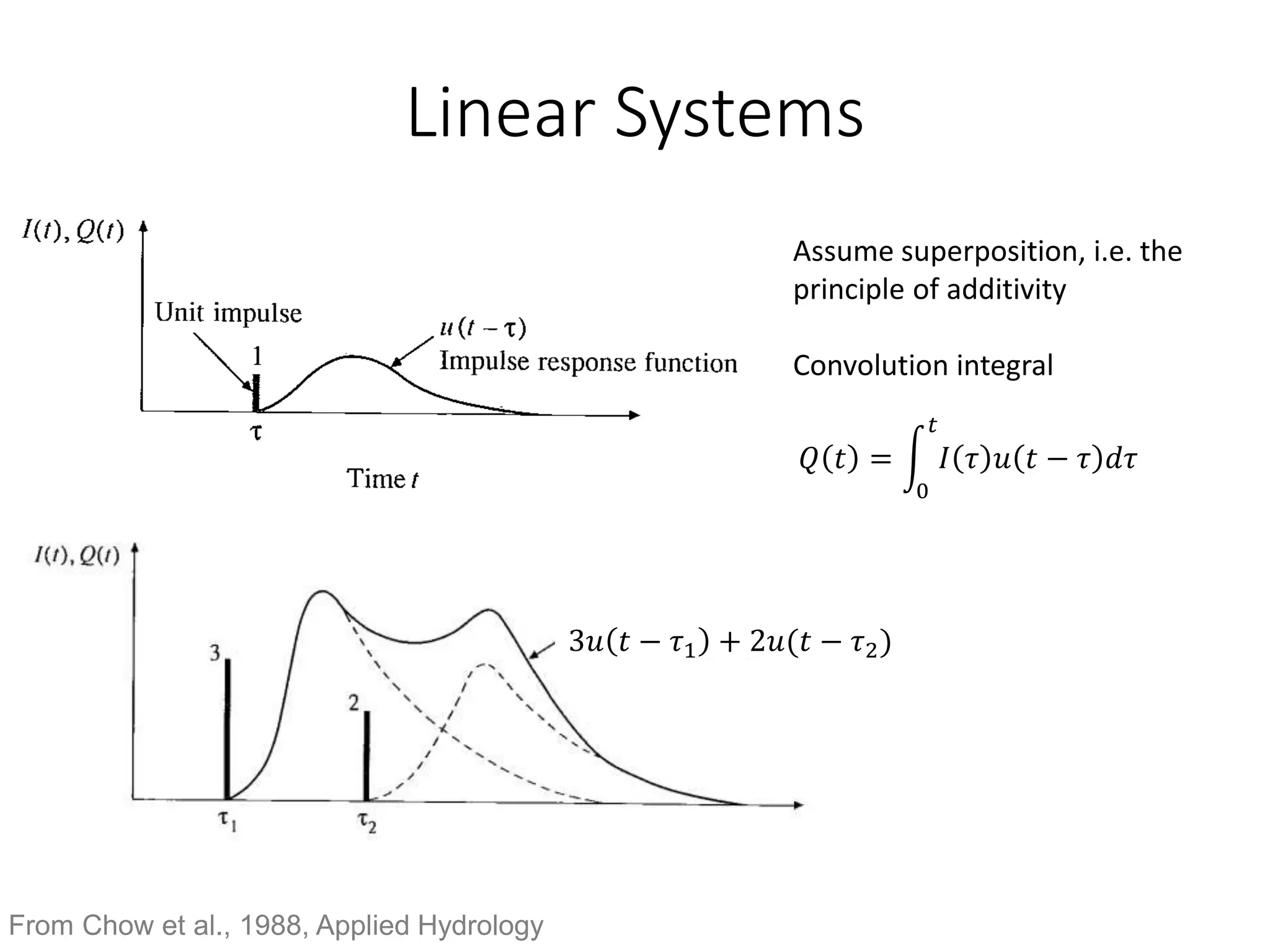
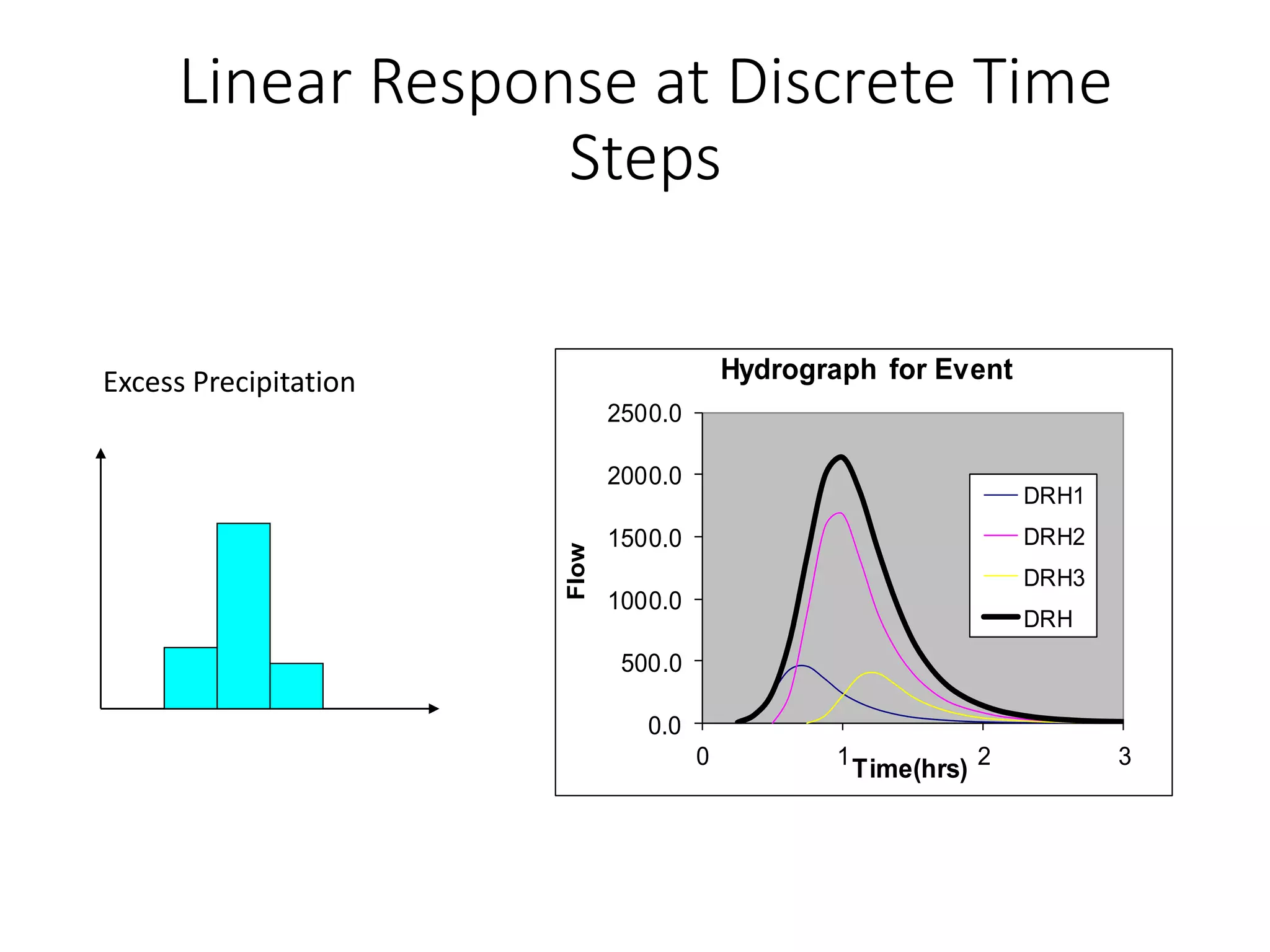
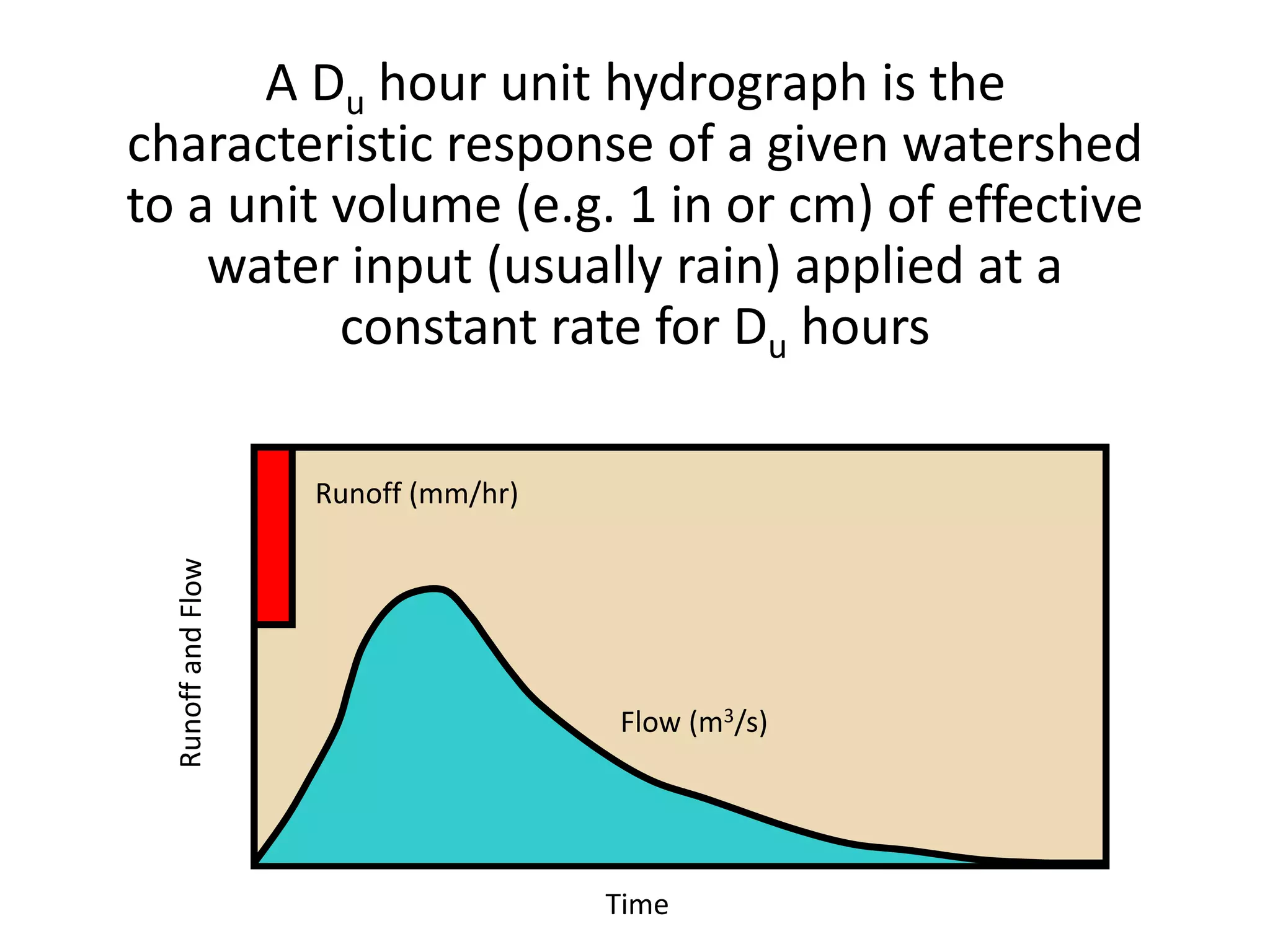
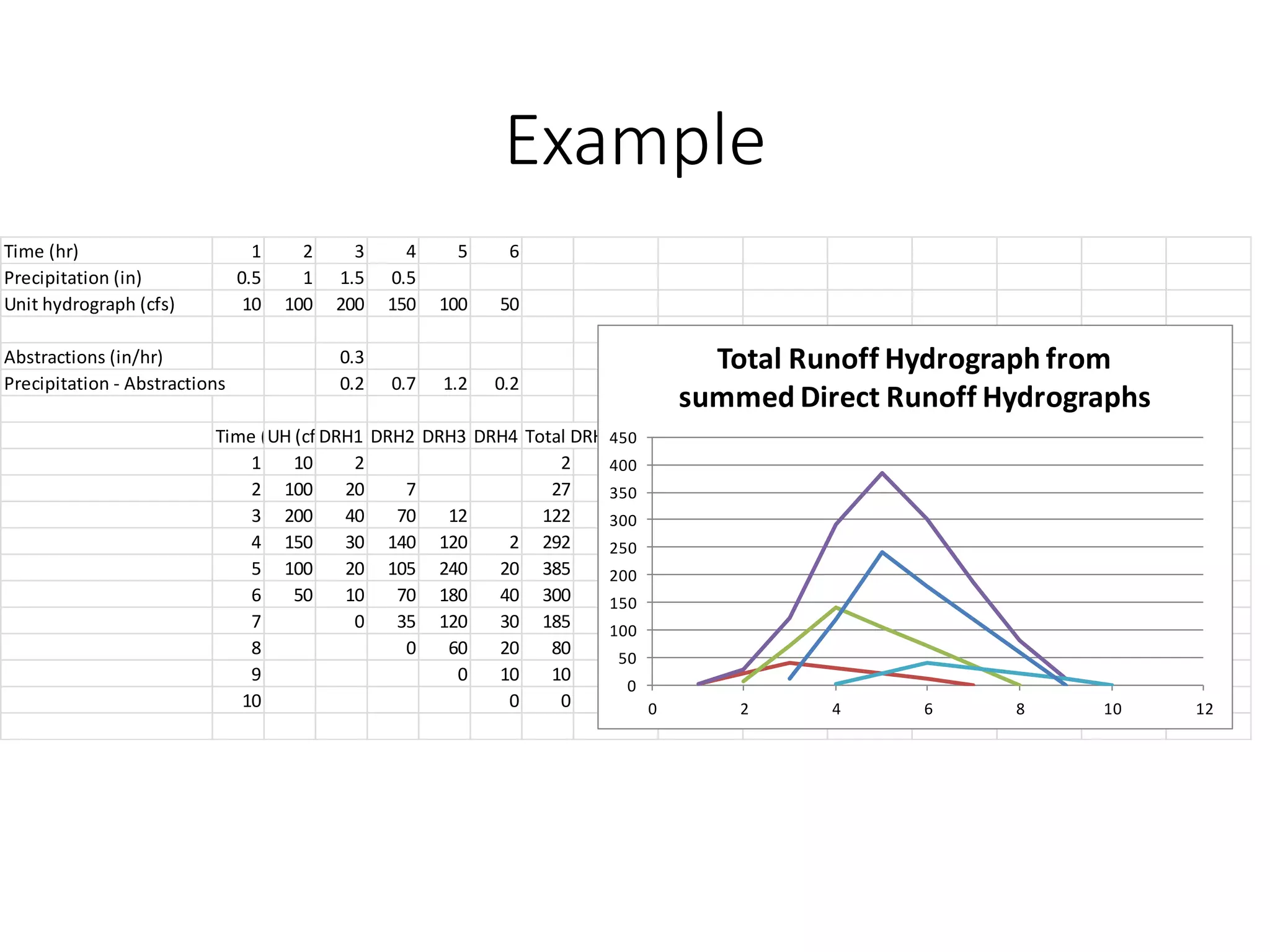
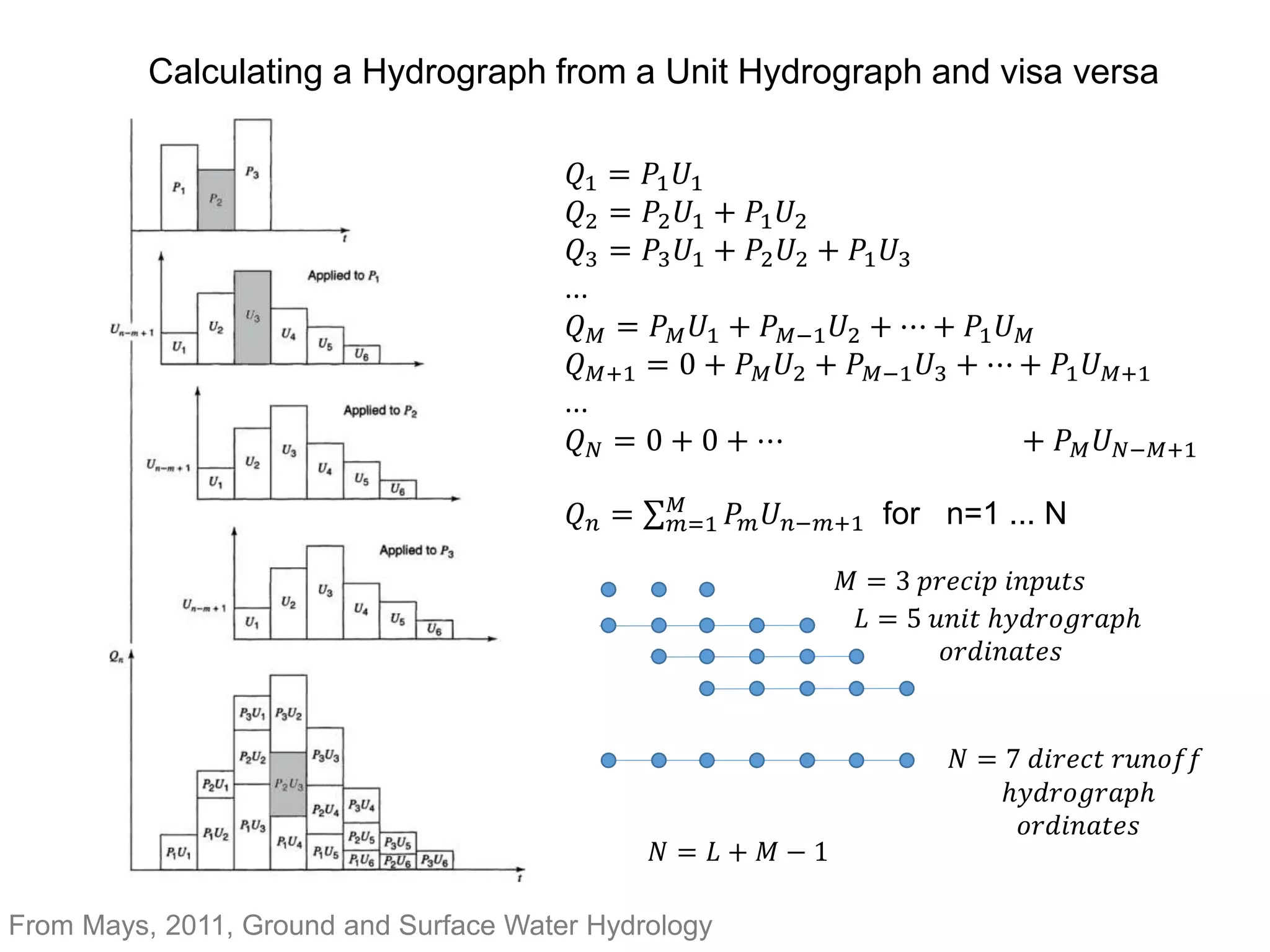
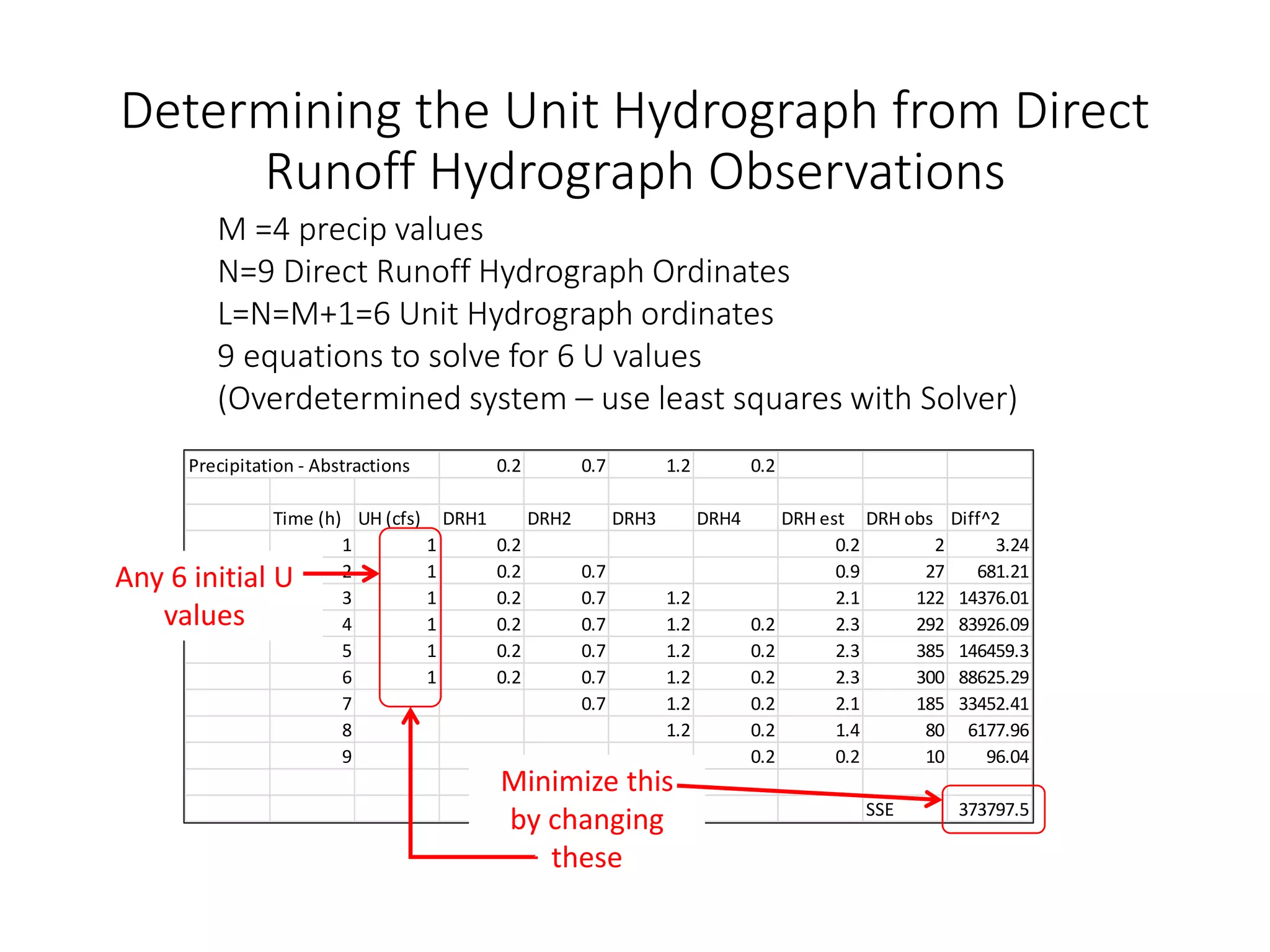
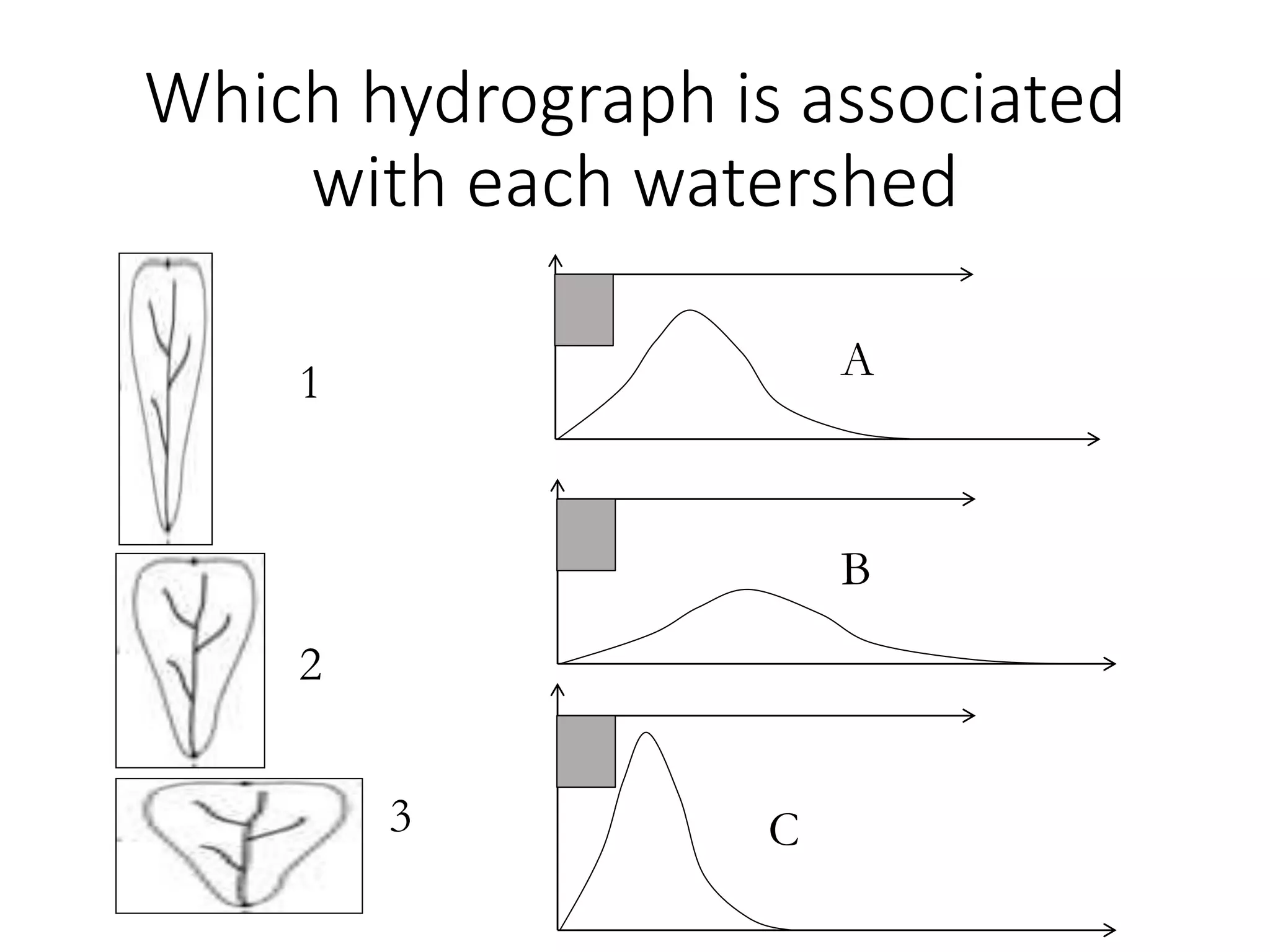
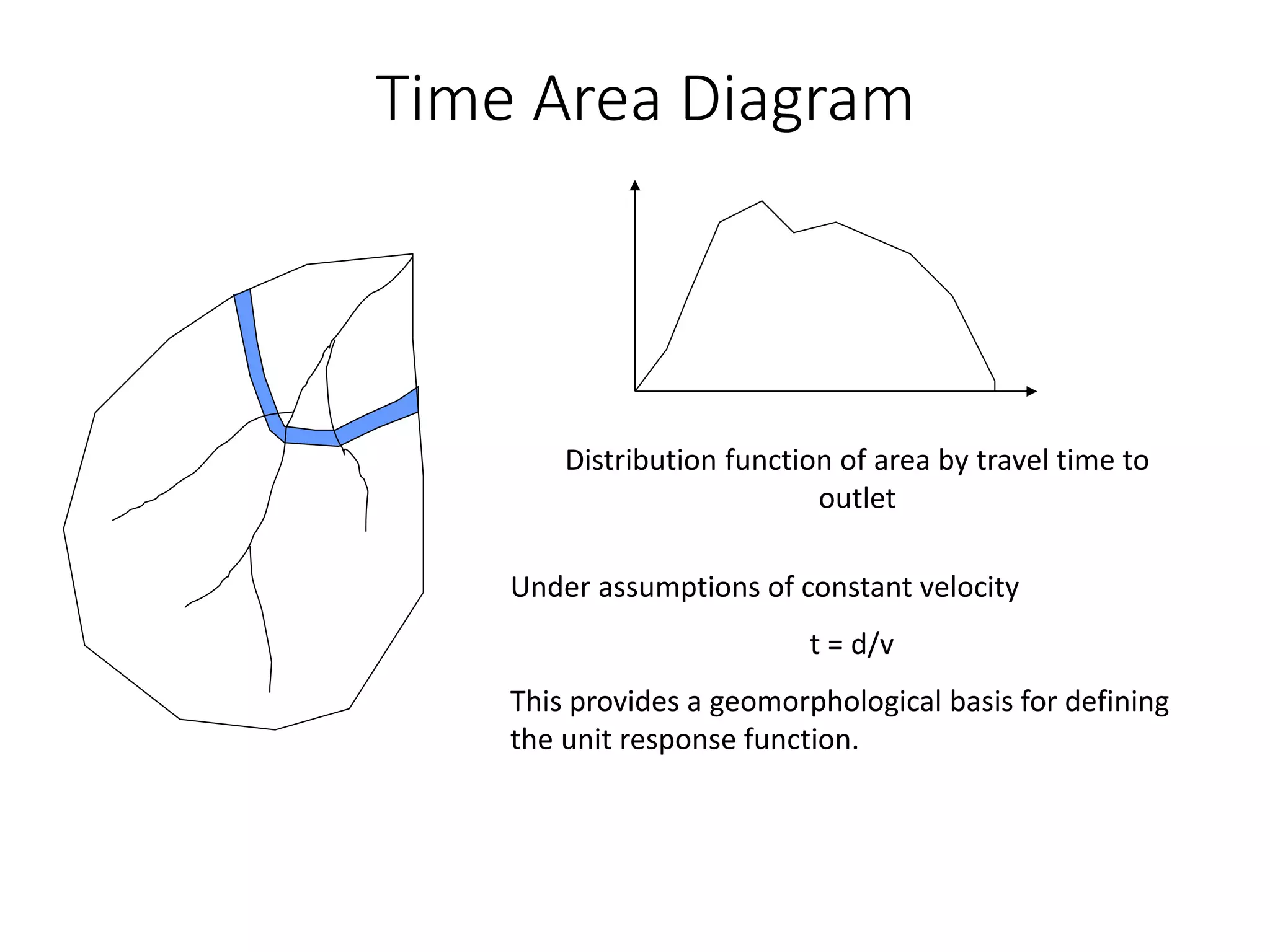
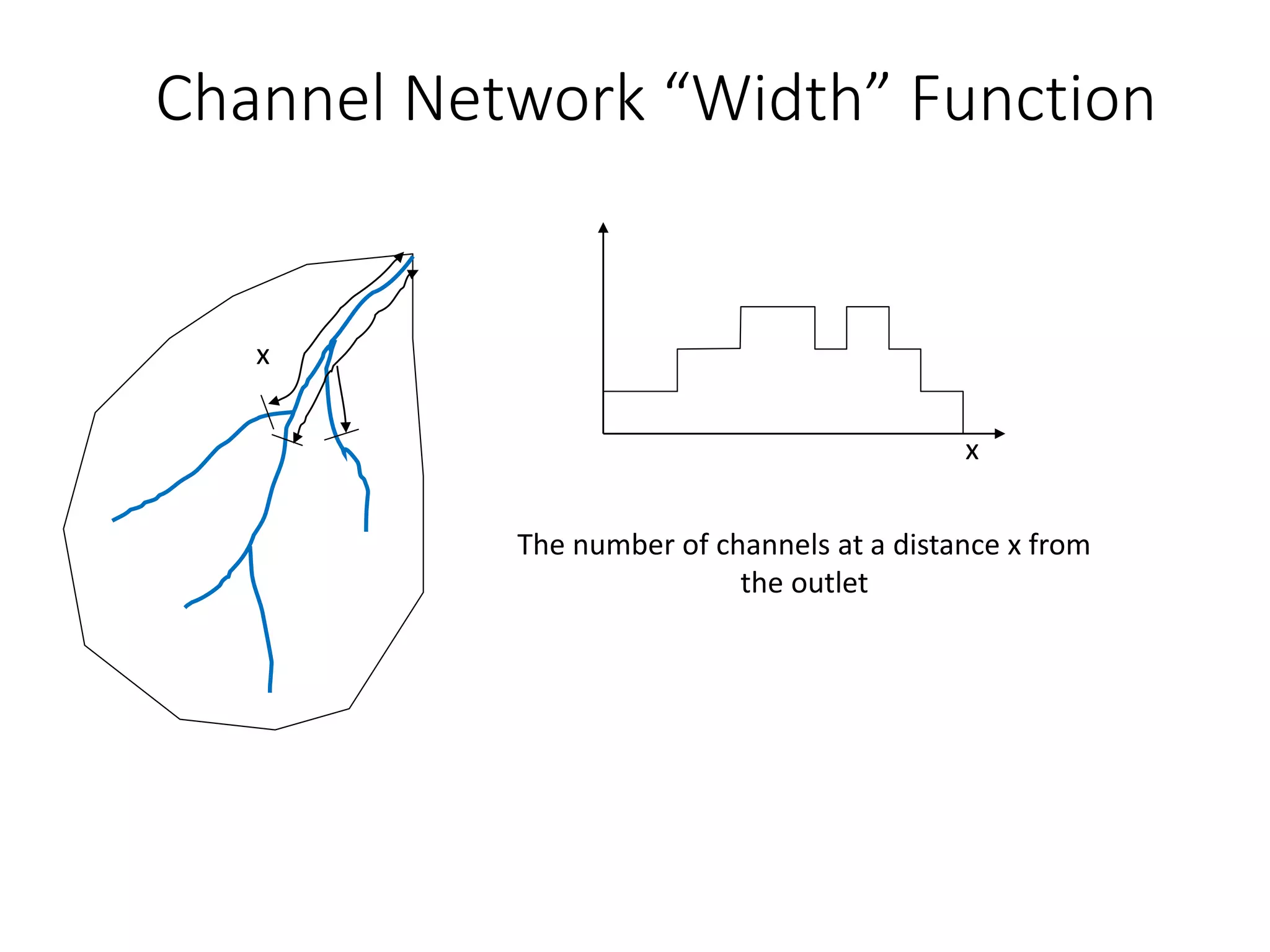
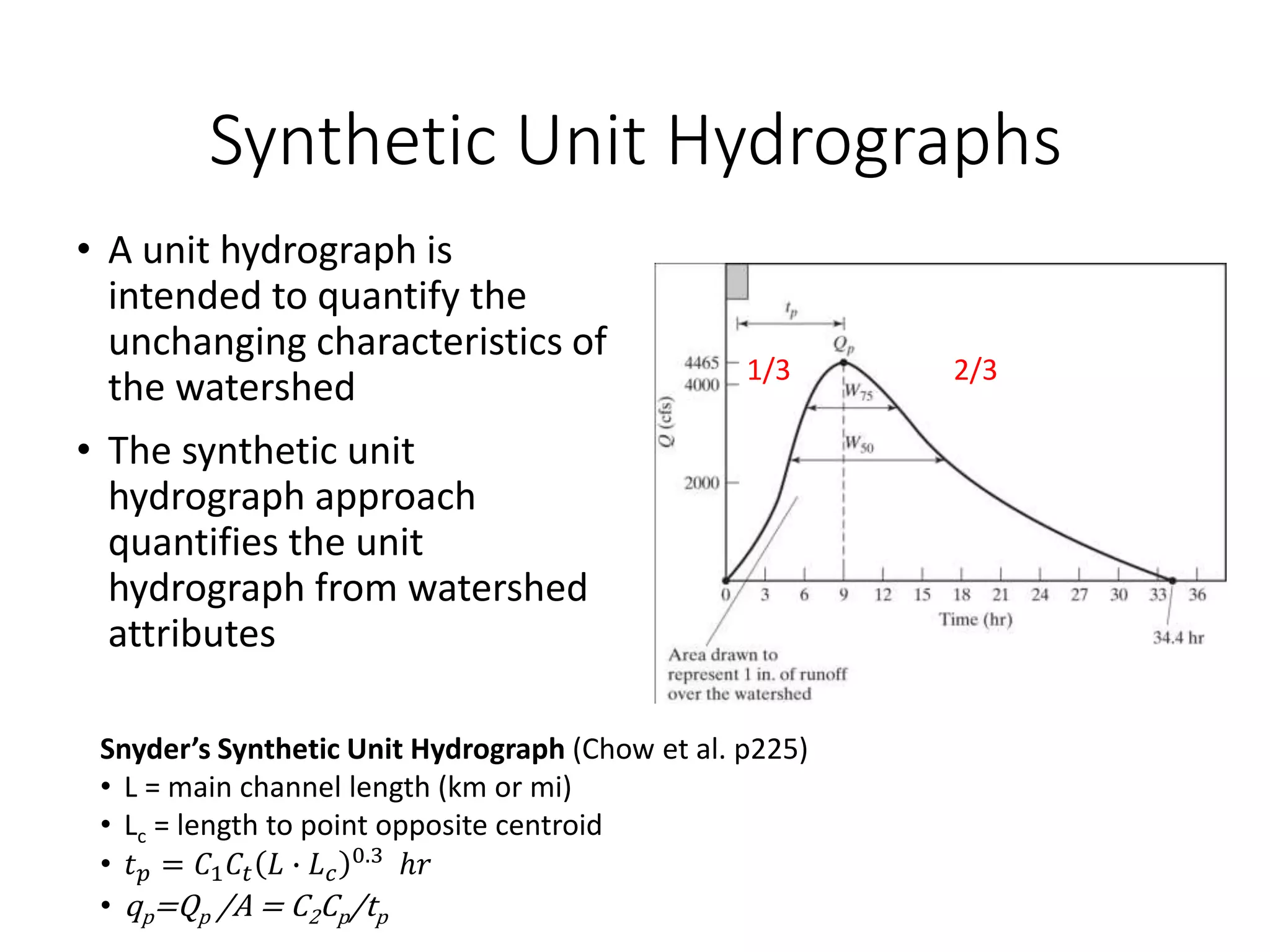
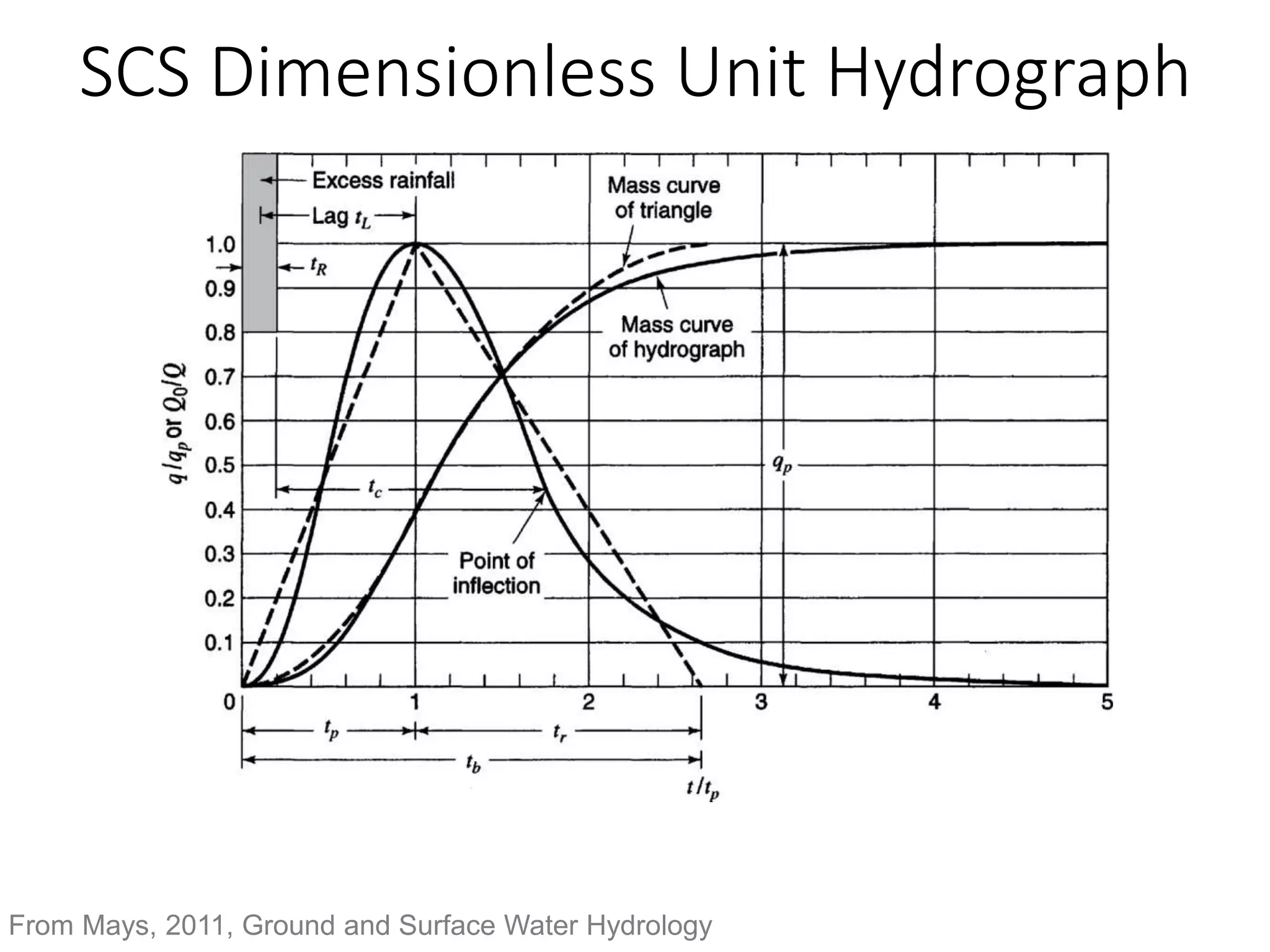
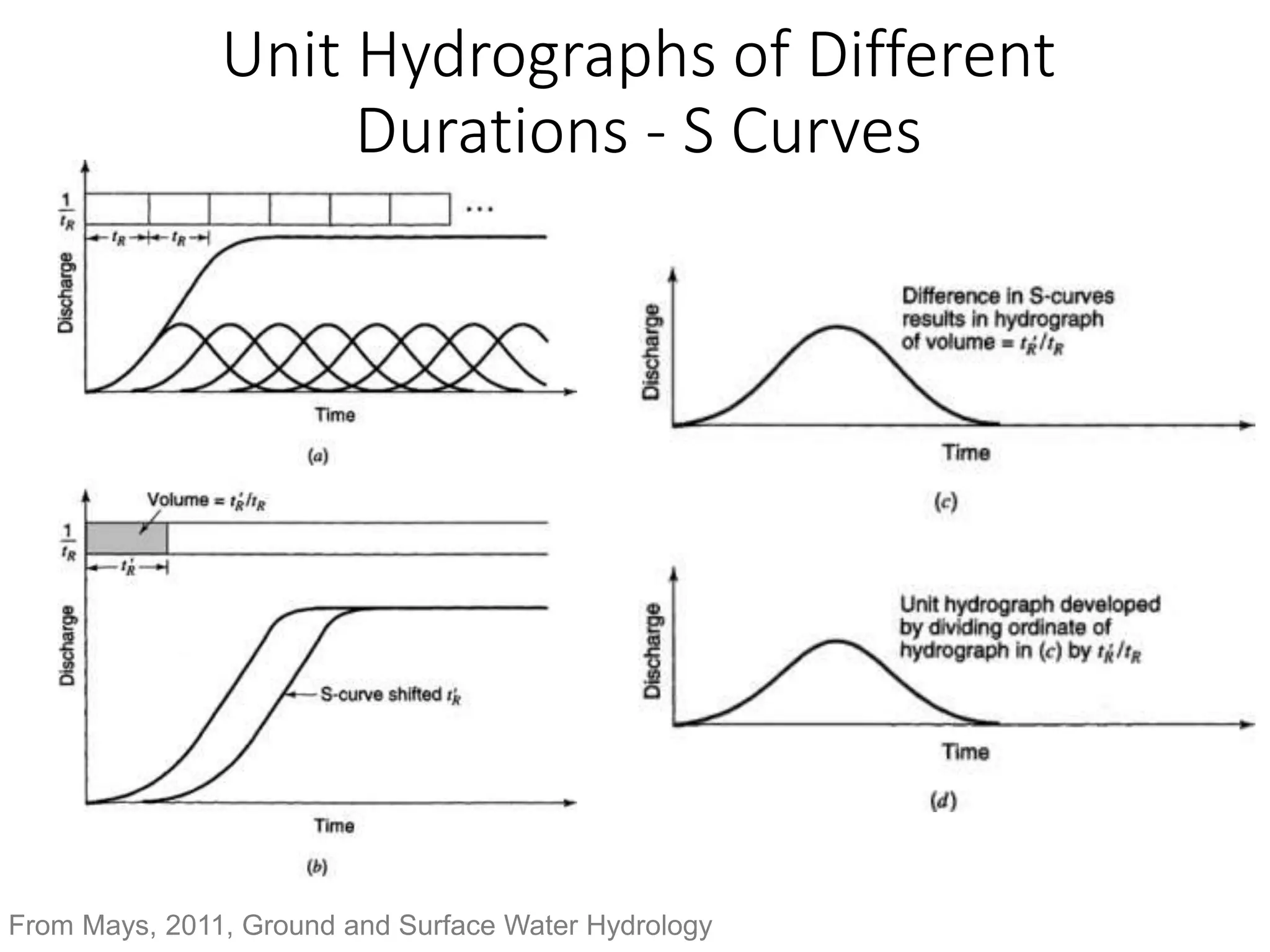
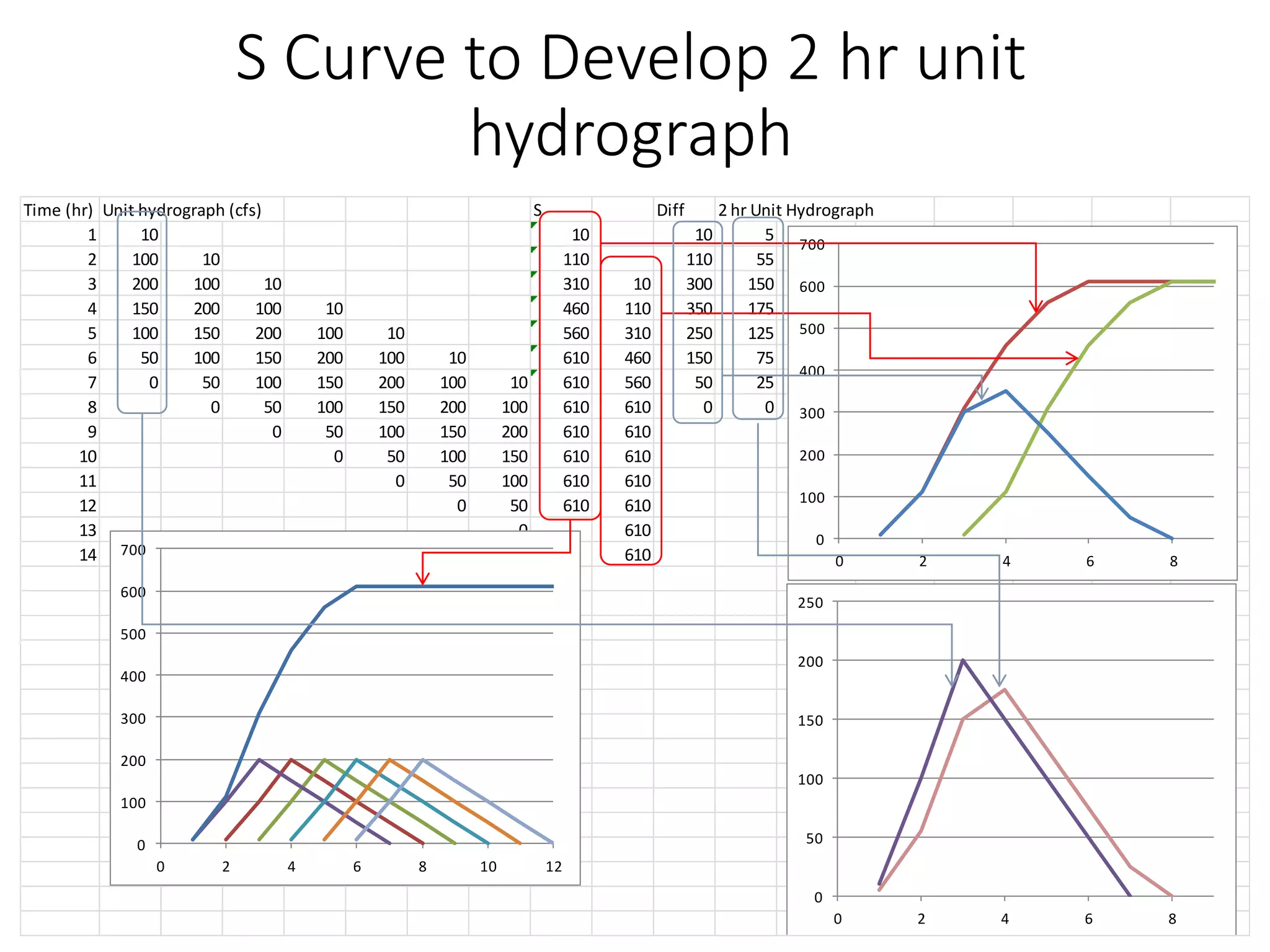
This document discusses unit hydrographs and linear response methods for calculating catchment response to precipitation events. It provides definitions of key hydrologic terms like unit hydrograph, excess precipitation, and direct runoff hydrograph. Methods are presented for calculating unit hydrographs from watershed characteristics and rainfall-runoff data, as well as for developing hydrographs from unit hydrographs. Examples are included to demonstrate these hydrograph analysis techniques.

1. Routing surface runoff to a basin
outlet
Learning objectives
• Be able to use stationary linear response methods
(unit hydrograph) to calculate catchment response
• Be able to estimate the unit hydrograph from data
• Be able to describe the assumptions, limitations and
uses of linear response methods
Chow, V. T., D. R. Maidment and L. W. Mays, (1988), Applied
Hydrology, McGraw Hill, 572 p. Chapter 7

2. Goal is to quantify watershed
response without consideration
of detailed subscale processes
Runoff (mm/hr)
Flow (m3/s)
Time
Flow = f(Runoff, Watershed hydrologic properties)

3. Systems approach to event flow
From Dingman, 2002, Physical Hydrology

4. Rainfall – Runoff Analysis
From Mays, 2011, Ground and Surface Water Hydrology

5. Linear Systems
3𝑢 𝑡 − 𝜏1 + 2𝑢(𝑡 − 𝜏2)
𝑄 𝑡 =
0
𝑡
𝐼 𝜏 𝑢 𝑡 − 𝜏 𝑑𝜏
From Chow et al., 1988, Applied Hydrology
Assume superposition, i.e. the
principle of additivity
Convolution integral

6. Linear Response at Discrete Time
Steps
Excess Precipitation
0.0
500.0
1000.0
1500.0
2000.0
2500.0
0 1 2 3
Flow
Time(hrs)
Hydrograph for Event
DRH1
DRH2
DRH3
DRH

7. A Du hour unit hydrograph is the
characteristic response of a given watershed
to a unit volume (e.g. 1 in or cm) of effective
water input (usually rain) applied at a
constant rate for Du hours
Runoff (mm/hr)
Flow (m3/s)
Time

8. Assumptions (Chow P 214)
• Excess rainfall has constant intensity within effective
duration
• Excess rainfall is uniformly distributed over watershed
• The base time of the direct runoff hydrograph from
an increment of excess rainfall is constant
• The ordinates of all direct runoff hydrographs are
proportional to the amount of direct runoff
• For a given watershed the hydrograph resulting from
a given excess rainfall reflects the unchanging
characteristics of the watershed

9. Calculating a Hydrograph from a Unit Hydrograph
𝑄1 = 𝑃1𝑈1
𝑄2 = 𝑃2𝑈1 + 𝑃1𝑈2
𝑄3 = 𝑃3𝑈1 + 𝑃2𝑈2 + 𝑃1𝑈3
...
𝑄𝑀 = 𝑃𝑀𝑈1 + 𝑃𝑀−1𝑈2 + ⋯ + 𝑃1𝑈𝑀
𝑄𝑀+1 = 0 + 𝑃𝑀𝑈2 + 𝑃𝑀−1𝑈3 + ⋯ + 𝑃1𝑈𝑀+1
...
𝑄𝑁 = 0 + 0 + ⋯ + 𝑃𝑀𝑈𝑁−𝑀+1
𝑄𝑛 = 𝑚=1
𝑀
𝑃𝑚𝑈𝑛−𝑚+1 for n=1 ... N
From Mays, 2011, Ground and Surface Water Hydrology
Chow page 217

10. Example
The 1- hr unit hydrograph for a watershed is given
below. Determine the runoff from this watershed for
the storm pattern given. The abstractions have a
constant rate of 0.3 in/ h.
Time ( hr) 1 2 3 4 5 6
Precipitation ( in) 0.5 1 1.5 0.5
Unit hydrograph ( cfs) 10 100 200 150 100 50

11. Example
Time (hr) 1 2 3 4 5 6
Precipitation (in) 0.5 1 1.5 0.5
Unit hydrograph (cfs) 10 100 200 150 100 50
Abstractions (in/hr) 0.3
Precipitation - Abstractions 0.2 0.7 1.2 0.2
Time (h)
UH (cfs)
DRH1 DRH2 DRH3 DRH4 Total DRH
1 10 2 2
2 100 20 7 27
3 200 40 70 12 122
4 150 30 140 120 2 292
5 100 20 105 240 20 385
6 50 10 70 180 40 300
7 0 35 120 30 185
8 0 60 20 80
9 0 10 10
10 0 0
0
50
100
150
200
250
300
350
400
450
0 2 4 6 8 10 12
Total Runoff Hydrograph from
summed Direct Runoff Hydrographs

12. Limitations
• Linearity is violated when deeper water flows
faster.
• Rainfall is seldom uniform in space
• Effective input is very uncertain and depends on
antecedent conditions

13. Example
Determine the 1- hr unit hydrograph for a watershed
using the precipitation pattern and runoff hydrograph
below. The abstractions have a constant rate of 0.3 in/
hr, and the baseflow of the stream is 0 cfs.
Time (h) 1 2 3 4 5 6 7 8 9 10
Precipitation (in) 0.5 1 1.5 0.5
Runoff (cfs) 2 27 122 292 385 300 185 80 10 0

14. Calculating a Hydrograph from a Unit Hydrograph and visa versa
𝑄1 = 𝑃1𝑈1
𝑄2 = 𝑃2𝑈1 + 𝑃1𝑈2
𝑄3 = 𝑃3𝑈1 + 𝑃2𝑈2 + 𝑃1𝑈3
...
𝑄𝑀 = 𝑃𝑀𝑈1 + 𝑃𝑀−1𝑈2 + ⋯ + 𝑃1𝑈𝑀
𝑄𝑀+1 = 0 + 𝑃𝑀𝑈2 + 𝑃𝑀−1𝑈3 + ⋯ + 𝑃1𝑈𝑀+1
...
𝑄𝑁 = 0 + 0 + ⋯ + 𝑃𝑀𝑈𝑁−𝑀+1
𝑄𝑛 = 𝑚=1
𝑀
𝑃𝑚𝑈𝑛−𝑚+1 for n=1 ... N
From Mays, 2011, Ground and Surface Water Hydrology
𝑀 = 3 𝑝𝑟𝑒𝑐𝑖𝑝 𝑖𝑛𝑝𝑢𝑡𝑠
𝐿 = 5 𝑢𝑛𝑖𝑡 ℎ𝑦𝑑𝑟𝑜𝑔𝑟𝑎𝑝ℎ
𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠
𝑁 = 7 𝑑𝑖𝑟𝑒𝑐𝑡 𝑟𝑢𝑛𝑜𝑓𝑓
ℎ𝑦𝑑𝑟𝑜𝑔𝑟𝑎𝑝ℎ
𝑜𝑟𝑑𝑖𝑛𝑎𝑡𝑒𝑠
𝑁 = 𝐿 + 𝑀 − 1

15. Determining the Unit Hydrograph from Direct
Runoff Hydrograph Observations
Precipitation - Abstractions 0.2 0.7 1.2 0.2
Time (h) UH (cfs) DRH1 DRH2 DRH3 DRH4 DRH est DRH obs Diff^2
1 1 0.2 0.2 2 3.24
2 1 0.2 0.7 0.9 27 681.21
3 1 0.2 0.7 1.2 2.1 122 14376.01
4 1 0.2 0.7 1.2 0.2 2.3 292 83926.09
5 1 0.2 0.7 1.2 0.2 2.3 385 146459.3
6 1 0.2 0.7 1.2 0.2 2.3 300 88625.29
7 0.7 1.2 0.2 2.1 185 33452.41
8 1.2 0.2 1.4 80 6177.96
9 0.2 0.2 10 96.04
SSE 373797.5
M =4 precip values
N=9 Direct Runoff Hydrograph Ordinates
L=N=M+1=6 Unit Hydrograph ordinates
9 equations to solve for 6 U values
(Overdetermined system – use least squares with Solver)
Any 6 initial U
values
Minimize this
by changing
these

16. Which hydrograph is associated
with each watershed
1
2
3
A
B
C

17. Time Area Diagram
Distribution function of area by travel time to
outlet
Under assumptions of constant velocity
t = d/v
This provides a geomorphological basis for defining
the unit response function.

18. Channel Network “Width” Function
The number of channels at a distance x from
the outlet
x
x

19. Synthetic Unit Hydrographs
• A unit hydrograph is
intended to quantify the
unchanging characteristics of
the watershed
• The synthetic unit
hydrograph approach
quantifies the unit
hydrograph from watershed
attributes
1/3 2/3
Snyder’s Synthetic Unit Hydrograph (Chow et al. p225)
• L = main channel length (km or mi)
• Lc = length to point opposite centroid
• 𝑡𝑝 = 𝐶1𝐶𝑡 𝐿 ∙ 𝐿𝑐
0.3 ℎ𝑟
• qp=Qp /A = C2Cp/tp

20. Example Snyder's Synthetic Unit
Hydrograph
A watershed has a drainage area of 5.42 mi2;
the length of the main stream is 4.45 mi, and
the main channel length from the watershed
outlet to the point opposite the center of
gravity of the watershed is 2.0 mi. Using Ct =
2.0 and Cp = 0.625, determine the standard
synthetic unit hydrograph for this basin. What
is the standard duration? Use Snyder’s
method to determine the 30- min unit
hydrograph parameter.
Follow the procedure of table 8.4.1
• L = main channel length = 4.45 mi
• Lc = length to point opposite centroid = 2.0 mi
• A = watershed area = 5.42 mi2
• 𝑡𝑝 = 𝐶1𝐶𝑡 𝐿 ∙ 𝐿𝑐
0.3
ℎ𝑟 = 1 ∙ 2 ∙ 4.45 ∙ 2 0.3
= 3.85 ℎ𝑟
• 𝑡𝑟 = 𝑡𝑝/5.5 = 0.7 ℎ𝑟
• 𝑡𝑝𝑅 = 𝑡𝑝 + 0.25 𝑡𝑅 − 𝑡𝑟 = 3.85 + 0.25 0.5 − 0.7 = 𝟑. 𝟖 𝒉𝒓
• 𝑄𝑝𝑅 =
𝐶2𝐶𝑝𝐴
𝑡𝑝𝑅
= 640 ∗ 0.625 ∗ 5.42/3.8 = 𝟓𝟕𝟎 𝒄𝒇𝒔
• Widths
• 𝑊75 =
𝐶75
𝑄𝑝𝑅/𝐴
1.08 =
440
570/5.42 1.08 = 2.88 ℎ𝑟
• 𝑊50 =
𝐶50
𝑄𝑝𝑅/𝐴
1.08 =
770
570/5.42 1.08 = 5.04 ℎ𝑟
• 𝑇𝑏 = 2581
𝐴
𝑄𝑝𝑅
− 1.5 𝑊50 − 𝑊75 = 2581
5.42
570
− 1.5 ∗ 5.04 −
2.88 = 14.1 ℎ𝑟
(2.37,285)
(3.09,427.5)
(4.05,570)
(5.97,427.5)
(7.41,285)
(14.1,0)
W50
W75
1/3 2/3

21. SCS Dimensionless Unit Hydrograph
From Mays, 2011, Ground and Surface Water Hydrology

22. Unit Hydrographs of Different
Durations - S Curves
From Mays, 2011, Ground and Surface Water Hydrology

23. Example
The 1- hr unit hydrograph for a watershed is given
below. Determine the 2 hr unit hydrograph.
Time ( hr) 1 2 3 4 5 6
Unit hydrograph ( cfs) 10 100 200 150 100 50

24. S Curve to Develop 2 hr unit
hydrograph
Time (hr) Unit hydrograph (cfs) S Diff 2 hr Unit Hydrograph
1 10 10 10 5
2 100 10 110 110 55
3 200 100 10 310 10 300 150
4 150 200 100 10 460 110 350 175
5 100 150 200 100 10 560 310 250 125
6 50 100 150 200 100 10 610 460 150 75
7 0 50 100 150 200 100 10 610 560 50 25
8 0 50 100 150 200 100 610 610 0 0
9 0 50 100 150 200 610 610
10 0 50 100 150 610 610
11 0 50 100 610 610
12 0 50 610 610
13 0 610
14 610
0
100
200
300
400
500
600
700
0 2 4 6 8
0
100
200
300
400
500
600
700
0 2 4 6 8 10 12
0
50
100
150
200
250
0 2 4 6 8