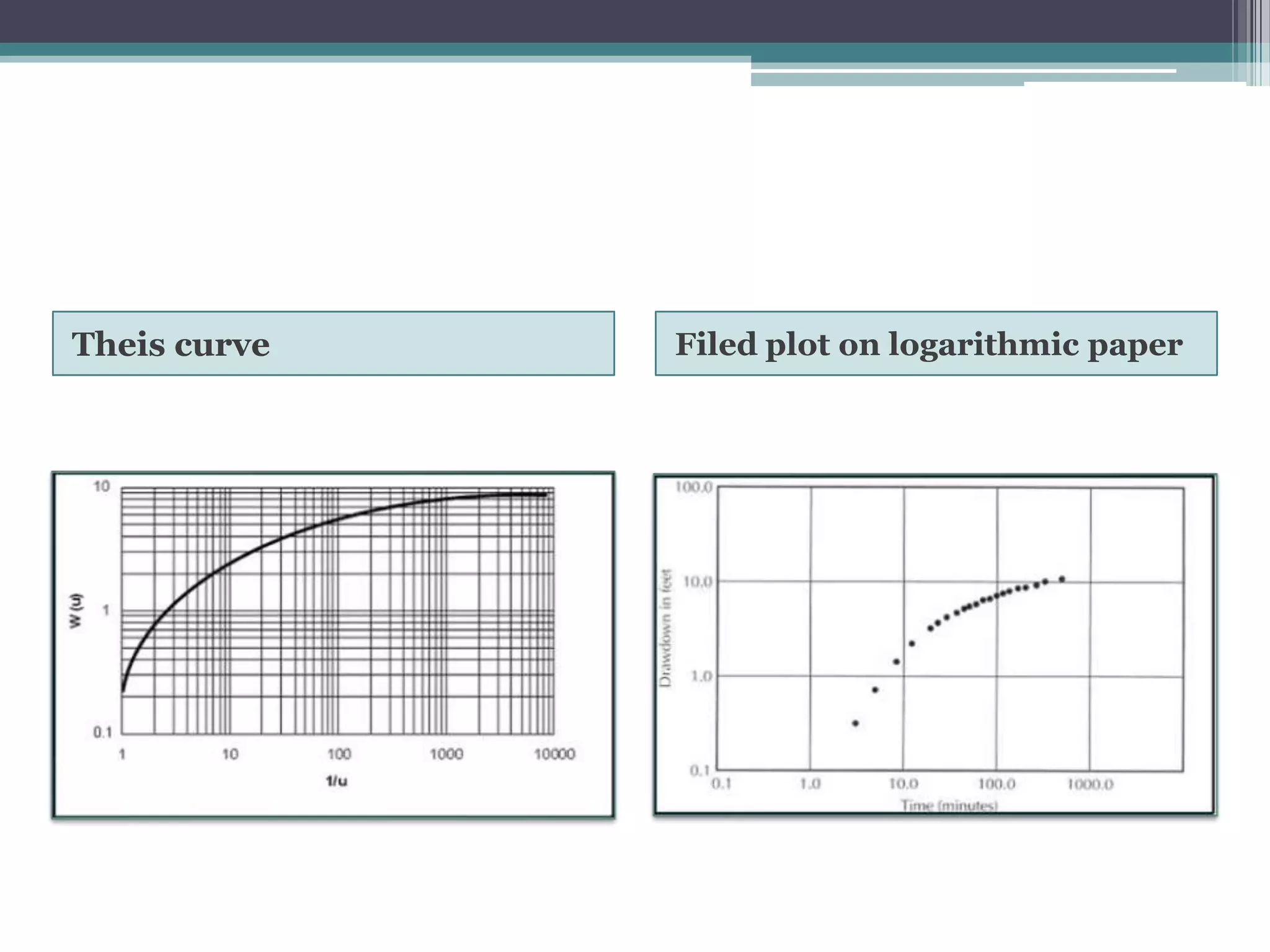
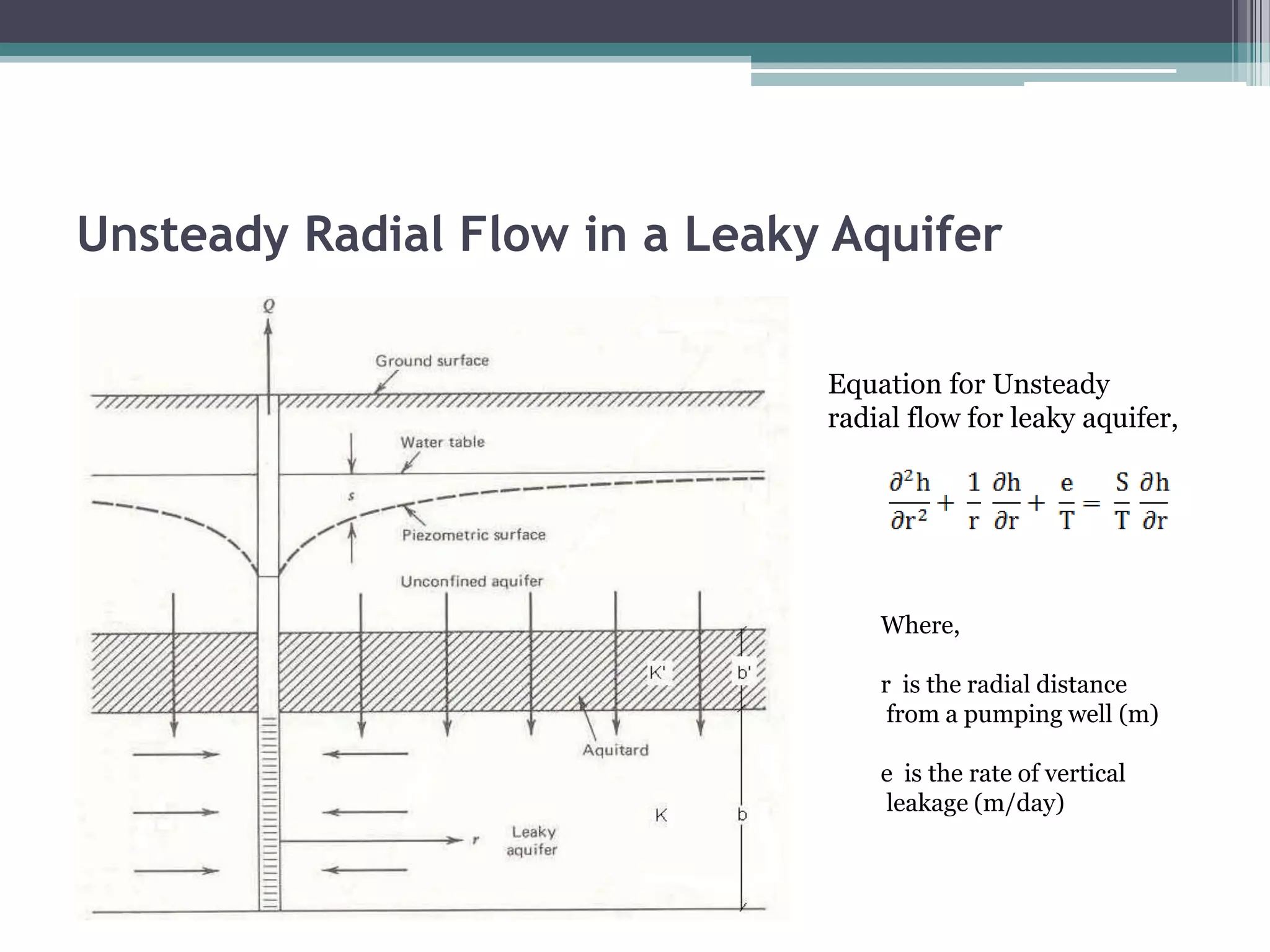
This document discusses unsteady radial flow in aquifers and methods for analyzing pumping test data. It describes equations for confined, unconfined, and leaky aquifers. The Theis and Cooper-Jacob methods are presented for analyzing confined aquifer data using type curves. For unconfined aquifers, Neuman's equation and the Penman method are described. The Hantush-Jacob solution and Walton graphical method are provided for analyzing pumping tests in leaky aquifers.

1. Aquifer and Non Equilibrium
equation for unsteady radial
flow
Presented by: AbhiShek Gupta

2. Aquifer
• A saturated, permeable, geologic unit that can transmit a
significant amount of groundwater under an ordinary
gradient.

3. Unsteady flow in confined aquifer
• Assumptions
 The aquifer is confined
 The aquifer has infinite aerial extent
 The aquifer is homogeneous, isotropic and of uniform thickness
 The piezometric surface is horizontal prior to pumping
 The aquifer is pumped at a constant discharge rate
 The well penetrates the full thickness of the aquifer and thus
receives water by horizontal flow

4. principle of continuity equation
of flow,
Inflow,
Outflow,

5. • Change in volume,
S (Storage coefficient) is the volume of water released per unit surface area per
unit change in head normal to the surface.
• In this equation, h is head, r is radial distance from the well, S is storage
coefficient, T is transmissivity, and t is the time since the beginning of pumping.

6. The Theis Method (Curve Matching Method)
• Theis assumed that the well is replaced by a mathematical sink of constant
strength and imposing the boundary conditions h = h0 for t = 0, and h → h0
as r →∞ for t ≥0, the solution,
Where W(u) is the well function and u is given by,

7. After taking log on both equations,
therefore, a graph of log s against log t should be the same shape as a graph of log
(W(u)) against log (1/u)
constants

8. Theis curve Filed plot on logarithmic paper

9. Match of field data plot to Theis Type curve

10. Cooper-Jacob Method (Time-Drawdown)
This is also based upon the Theis analysis
Base 10
Straight line

11. If and are drawdown at time
and then,
Transmissivity is calculated by above
equation.
When s=0
(storativity)
Semi –log plot

12. Cooper-Jacob Method (Distance-Drawdown)
When observation of 3 or more wells are to be made.
transmissivity, per one logarithmic cycle
When s=0,
Therefore,

13. Unsteady Radial Flow in an Unconfined Aquifer
Equation of flow of water (Neuman’s equation),
where,
h is the saturated thickness of the aquifer (m)
r is radial distance from the pumping well (m)
z is elevation above the base of the aquifer (m)
is specific storage (1/m)
is radial hydraulic conductivity (m/day)
is vertical hydraulic conductivity (m/day)
T is time (day)

14. Three phases of drawdown
First phase:
• pressure drops
• specific storage as a major
contribution behaves as an
artesian aquifer
•flow is horizontal
• time-drawdown follows
Theis curve S - the elastic
storativity.

15. Second phase Third phase
• water table declines
• specific yield as a major
contribution
• flow is both horizontal and
vertical
• time-drawdown is a function
of Kv/Kh r, b
• rate of drawdown decreases
• flow is again horizontal
• time-drawdown again follows
Theis curve S - the specific
yield.

16. Neuman’ assumptions
• The aquifer is unconfined.
• The vadose zone has no influence on the drawdown.
• Water initially pumped comes from the instantaneous release of water from elastic
storage.
• Eventually water comes from storage due to gravity drainage of interconnected
pores.
• The drawdown is negligible compared with the saturated aquifer thickness.
• The specific yield is at least 10 times the elastic storativity.
• The aquifer may be- but does not have to be- anisotropic with the radial hydraulic
conductivity different than the vertical hydraulic conductivity.

17. Neuman’s solution,
Where,
is the well function of water-table aquifer
For early time,
and
For late time, and
and
Parameters can be
found by Penman
method

18. Penmen method to find parameters
• Two sets of type curves are used and plotted on log-log paper (Theoretical curve
vs 1/u).
• Superpose the early (t − s) data on Type-A curve.
• The data analysis is done by matching the observed data to the type curve.
• From the match point of Type-A curve, determine the values for
and the value of
• Use the previous equations to determine T and S
• The latest (s − t) data are then superposed on Type-B Curve for the Γ - values of
previously matched Type-A curve, from the match point of Type-B curve, determine
the values for
• By using the previous equations, the T and S can be determined.
.

19. Type curves for unconfined aquifers

20. Unsteady Radial Flow in a Leaky Aquifer
Equation for Unsteady
radial flow for leaky aquifer,
Where,
r is the radial distance
from a pumping well (m)
e is the rate of vertical
leakage (m/day)

21. Hantush-Jacob Method
Assumptions:
• The aquifer is leaky and has an "apparent" infinite extent,
• The aquifer and the confining layer are homogeneous, isotropic, and of uniform
thickness, over the area influenced by pumping,
• The potentiometric surface was horizontal prior to pumping,
• The well is pumped at a constant rate,
• The well is fully penetrating,
• Water removed from storage is discharged instantaneously with decline in head,
• The well diameter is small so that well storage is negligible,
• Leakage through the aquitard layer is vertical.

22. Hantush and Jacob solution for leaky aquifer,
Where,
where,
is the well function for leaky confined aquifer
B is the leakage factor given as
where,
b' is thickness of the aquitard (m)
K' is hydraulic conductivity of the aquitard (m/day)

23. Walton Graphical Solution
Log-log plot

24. Procedure
• Field data are plotted on drawdown vs. time on full logarithmic
scale.
• Field data should match one of the type curves for r/B
(interpolation if between two lines)
• From a match point, the following are known values
• Substitute in Hantush-Jacob equation:
(From match) r = distance between pumping well and
observation well
B = leakage factor

25. Thank you