TWO TRIANGLES HAVING THE SAME BASE AND EQUAL AREAS LIE BETWEEN THE SAME PARALLELS
•Download as PPTX, PDF•
0 likes•4,412 views
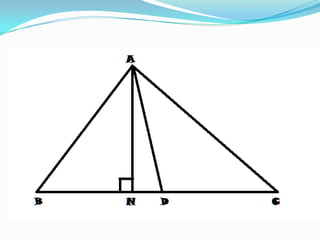
The document provides two examples of geometric proofs involving areas of shapes. The first example proves that a triangle's median divides it into two equal areas. It does so by drawing an altitude and showing the two resulting triangles have the same base and altitude. The second example proves the area of a quadrilateral ABCD equals the area of triangle ADE by showing two triangles on the same base and between parallel lines have equal areas.
Report
Share
Report
Share
Recommended
areas_of_parallelograms_and_triangles
The document discusses areas of parallelograms and triangles. It contains examples of figures that lie on the same base and between the same parallels. It also contains problems calculating the areas of various shapes formed from parallelograms and triangles. One problem involves a farmer dividing a parallelogram-shaped field into three triangular parts by drawing a line between two vertices, and requiring the crops to be sown in equal areas.
areas of triangles and parallelograms
The document discusses geometry and formulas for calculating the areas of different shapes. It begins by explaining how geometry originated from measuring land areas. It then reviews key concepts like planar regions and formulas for finding the areas of rectangles, squares, parallelograms, and triangles. The main part proves theorems about the areas of figures on the same base and between the same parallels, including that parallelograms in this position have equal areas, and triangles in this position have half the area of the corresponding parallelogram. It concludes by listing five proofs as examples.
Area of triangles and IIgm
The document discusses triangles, parallelograms, and congruent figures in geometry. It defines triangles and parallelograms, explains how to calculate their areas, and presents three theorems: 1) Parallelograms on the same base and between the same parallels have equal areas. 2) A diagonal of a parallelogram divides it into two triangles of equal area. 3) The area of a triangle in a parallelogram is equal to half the area of the parallelogram. Proofs of the theorems are provided based on properties of parallel lines, congruent triangles, and calculations of area.
Area of parallelograms and triangles
This document discusses properties of parallelograms, triangles, and calculating their areas. It defines a parallelogram as a quadrilateral with both pairs of opposite sides parallel. Properties include opposite sides being parallel and congruent. It defines a triangle as a three-sided polygon. It explains that the area of a shape is a number associated with the enclosed plane region, with equal areas for congruent shapes and the sum of areas for shapes that combine. It discusses congruent figures having equal areas but not vice versa, and that parallelograms and triangles on the same base or between parallels have equal areas.
Gch04 l5
This document discusses different methods for proving triangles congruent:
- ASA (Angle-Side-Angle) congruence can be used if two angles and the included side are congruent.
- AAS (Angle-Angle-Side) congruence can be used if two angles of one triangle are congruent to two angles of another triangle and one side included between the angles is congruent.
- HL (Hypotenuse-Leg) congruence can be used if two right triangles have one leg and the hypotenuse congruent.
Examples are provided to demonstrate applications of each method of triangle congruence.
Vectors parrallel and coplanar
- The objectives of the lesson are to: add and subtract vectors using line segments, identify coplanar and parallel vectors using scalar multiples, and express coplanar and parallel vectors as a ratio.
- Key concepts covered include vector addition and subtraction, scalar multiples, ratios of vectors, and identifying parallel vectors.
- Examples are provided to demonstrate how to write vectors in terms of variables, find ratios of vectors, and express vectors in terms of given variables using properties of parallel vectors and scalar multiples.
Geom 6point3 97
This document discusses several theorems for proving that a quadrilateral is a parallelogram:
1) If both pairs of opposite sides of a quadrilateral are congruent, then it is a parallelogram.
2) If both pairs of opposite angles of a quadrilateral are congruent, then it is a parallelogram.
3) If an angle of a quadrilateral is supplementary to both of its consecutive angles, then it is a parallelogram.
The document also provides proofs of these theorems and discusses using coordinate geometry to prove sides are congruent or parallel.
Gch04 l4
This document discusses triangle congruence using the Side-Side-Side (SSS) and Side-Angle-Side (SAS) postulates. It provides examples of using SSS and SAS to prove that two triangles are congruent. Key concepts covered include triangle rigidity, included angles, and applying SSS and SAS to solve problems and construct congruent triangles. Worked examples demonstrate using SSS and SAS, along with step-by-step proofs of triangle congruence.
Recommended
areas_of_parallelograms_and_triangles
The document discusses areas of parallelograms and triangles. It contains examples of figures that lie on the same base and between the same parallels. It also contains problems calculating the areas of various shapes formed from parallelograms and triangles. One problem involves a farmer dividing a parallelogram-shaped field into three triangular parts by drawing a line between two vertices, and requiring the crops to be sown in equal areas.
areas of triangles and parallelograms
The document discusses geometry and formulas for calculating the areas of different shapes. It begins by explaining how geometry originated from measuring land areas. It then reviews key concepts like planar regions and formulas for finding the areas of rectangles, squares, parallelograms, and triangles. The main part proves theorems about the areas of figures on the same base and between the same parallels, including that parallelograms in this position have equal areas, and triangles in this position have half the area of the corresponding parallelogram. It concludes by listing five proofs as examples.
Area of triangles and IIgm
The document discusses triangles, parallelograms, and congruent figures in geometry. It defines triangles and parallelograms, explains how to calculate their areas, and presents three theorems: 1) Parallelograms on the same base and between the same parallels have equal areas. 2) A diagonal of a parallelogram divides it into two triangles of equal area. 3) The area of a triangle in a parallelogram is equal to half the area of the parallelogram. Proofs of the theorems are provided based on properties of parallel lines, congruent triangles, and calculations of area.
Area of parallelograms and triangles
This document discusses properties of parallelograms, triangles, and calculating their areas. It defines a parallelogram as a quadrilateral with both pairs of opposite sides parallel. Properties include opposite sides being parallel and congruent. It defines a triangle as a three-sided polygon. It explains that the area of a shape is a number associated with the enclosed plane region, with equal areas for congruent shapes and the sum of areas for shapes that combine. It discusses congruent figures having equal areas but not vice versa, and that parallelograms and triangles on the same base or between parallels have equal areas.
Gch04 l5
This document discusses different methods for proving triangles congruent:
- ASA (Angle-Side-Angle) congruence can be used if two angles and the included side are congruent.
- AAS (Angle-Angle-Side) congruence can be used if two angles of one triangle are congruent to two angles of another triangle and one side included between the angles is congruent.
- HL (Hypotenuse-Leg) congruence can be used if two right triangles have one leg and the hypotenuse congruent.
Examples are provided to demonstrate applications of each method of triangle congruence.
Vectors parrallel and coplanar
- The objectives of the lesson are to: add and subtract vectors using line segments, identify coplanar and parallel vectors using scalar multiples, and express coplanar and parallel vectors as a ratio.
- Key concepts covered include vector addition and subtraction, scalar multiples, ratios of vectors, and identifying parallel vectors.
- Examples are provided to demonstrate how to write vectors in terms of variables, find ratios of vectors, and express vectors in terms of given variables using properties of parallel vectors and scalar multiples.
Geom 6point3 97
This document discusses several theorems for proving that a quadrilateral is a parallelogram:
1) If both pairs of opposite sides of a quadrilateral are congruent, then it is a parallelogram.
2) If both pairs of opposite angles of a quadrilateral are congruent, then it is a parallelogram.
3) If an angle of a quadrilateral is supplementary to both of its consecutive angles, then it is a parallelogram.
The document also provides proofs of these theorems and discusses using coordinate geometry to prove sides are congruent or parallel.
Gch04 l4
This document discusses triangle congruence using the Side-Side-Side (SSS) and Side-Angle-Side (SAS) postulates. It provides examples of using SSS and SAS to prove that two triangles are congruent. Key concepts covered include triangle rigidity, included angles, and applying SSS and SAS to solve problems and construct congruent triangles. Worked examples demonstrate using SSS and SAS, along with step-by-step proofs of triangle congruence.
CLASS IX MATHS 6 areas of parallelogram and triangles
The document discusses relationships between the areas of plane figures such as parallelograms, triangles, and rectangles that share the same base or lie between the same parallels. It defines what it means for figures to be on the same base and between the same parallels. The key points are that parallelograms on the same base and between the same parallels have equal areas, and triangles on the same base and between the same parallels also have equal areas. Formulas for calculating the areas of parallelograms and triangles are reviewed.
Geometry 201 unit 4.2
This document provides instruction on proving triangle congruence using the Side-Side-Side (SSS) and Side-Angle-Side (SAS) postulates. It includes examples of using SSS and SAS to show that triangles are congruent, as well as practice problems for students to verify congruence. Key concepts covered are triangle rigidity, included angles, and applying SSS and SAS to real-world geometry problems.
4.2 Congruence and Triangles
Here are 3 practice problems from the textbook:
14. ΔABC ≅ ΔXYZ. Find m∠A if m∠X = 50°.
16. ΔDEF ≅ ΔGHI. If DF = 12 and GH = 8, find IH.
35. Prove: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are congruent.
Similarity of triangles -GEOMETRY
- Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
- There are three criteria for similarity of triangles: AAA (if corresponding angles are equal), SSS (if corresponding sides are proportional), and SAS (if one angle is equal and the sides containing those angles are proportional).
- If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, the triangles on each side of the perpendicular are similar to each other and to the original triangle.
6.6 proportions & similar triangles
This document discusses proportionality theorems and using similar triangles to solve problems involving segment lengths. It provides 6 theorems regarding proportional line segments in triangles and parallel lines cut by transversals. Examples are given to demonstrate using the theorems to find unknown segment lengths. Real-life applications involving building construction are also presented.
Teacher lecture
This document provides an introduction to congruent triangles and the different methods to prove triangles are congruent: SSS, SAS, and ASA. It includes examples of using side and angle correspondences to show triangles are congruent according to the three congruence rules. Students are asked to complete a KWL chart on triangles as an exit ticket.
Module5 dodong2
This document provides instruction and content for a Grade 9 mathematics module on parallelograms. It includes definitions of parallelograms and their properties. Several theorems are proved, including those regarding parallelograms, rectangles, rhombuses, the midline theorem, trapezoids, and kites. Example problems are also provided to demonstrate applying the properties and theorems of parallelograms.
Lecture 4.3
The document discusses congruent triangles and their properties. It defines congruent figures as those with corresponding sides and angles that are congruent. It presents several ways to prove triangles are congruent, including using corresponding parts, vertical angles, the third angle theorem, and properties of congruent figures like the transitive property. It provides examples of writing congruence statements and determining if triangles are congruent based on given information.
Congruent triangles
The document discusses various properties and theorems related to triangles. It begins by defining different types of triangles based on side lengths and angle measures. It then covers the four congruence rules for triangles: SAS, ASA, AAS, and SSS. The document proceeds to prove several theorems about relationships between sides and angles of triangles, such as opposite sides/angles of isosceles triangles being equal, larger sides having greater opposite angles, and the sum of any two angles being greater than the third side. It concludes by proving that the perpendicular from a point to a line is the shortest segment.
7.4 Similarity in right triangles
This document discusses similar right triangles and the geometric mean. It contains examples and theorems about how cutting an altitude to the hypotenuse of a right triangle divides it into two similar right triangles. The geometric mean of two numbers a and b is the positive number x that satisfies ab=x^2. Using the geometric mean and properties of similar triangles, missing side lengths can be calculated.
Right Triangle Similarity
The document discusses similarity in right triangles. It states that drawing an altitude to the hypotenuse of a right triangle divides it into two smaller right triangles that are similar to each other and the original triangle. The altitude also allows one to find missing side lengths using geometric mean formulas. Several examples are given of using these formulas to solve for missing lengths in right triangles.
6.6 use proportionality theorems
This document discusses proportionality theorems and their applications to solving geometry problems involving similar triangles. It provides 4 examples of using proportionality theorems to find unknown side lengths. Specifically, it uses the Triangle Proportionality Theorem, which states that if two triangles are cut by a transversal, then the ratios of the lengths of the corresponding sides are equal. It also uses properties of parallel lines and proportions. The document concludes with guided practice and exit slip problems for students to apply proportionality theorems.
Triangles For Class 10 CBSE NCERT
The document describes how to determine if three lines will form a triangle based on their lengths. It states that if the sum of the lengths of the two shortest lines is less than the longest line, the lines will not form a triangle. If the sum is equal to the longest line, the two shortest lines will overlap the longest line. Only if the sum is greater than the longest line will the three lines form a triangle.
Obj. 19 CPCTC
This document discusses the concept of CPCTC (Corresponding Parts of Congruent Triangles are Congruent). It states that once two triangles are proven to be congruent using SSS, SAS, ASA, AAS, or HL, then all corresponding parts of those triangles are also congruent due to CPCTC. It provides two examples of using CPCTC to prove corresponding angles are congruent after first showing the triangles are congruent using given information.
Cogruence
The document discusses congruence and similarity of triangles and figures. It defines congruence as two figures having equal corresponding sides and angles. Similarity requires proportional corresponding sides and equal corresponding angles. The conditions for congruence of triangles are: side-side-side, side-angle-side, angle-side-angle, and angle-angle-side. Congruence is reflexive, symmetric, and transitive. The conditions for similarity of triangles are: corresponding sides proportional and two or more equal corresponding angles.
Congruence of Triangle
The document discusses different rules for determining if two triangles are congruent, including:
- The ASA (Angle-Side-Angle) rule, which states two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle. An example proof of this rule is provided.
- The SSS (Side-Side-Side) rule, which states two triangles are congruent if three sides of one triangle are equal to the corresponding three sides of the other triangle. An example proof is also provided.
- The Hypotenuse-Leg rule, which states two right triangles are congruent if the hypotenuse and one side of one
Quadrilaterals Theorems
The document contains several theorems about the properties of parallelograms: if a quadrilateral has both pairs of opposite sides congruent, opposite angles congruent, or an angle supplementary to its consecutive angles, then it is a parallelogram. It also proves that if the diagonals of a quadrilateral bisect each other or one pair of opposite sides are congruent and parallel, then it is a parallelogram. This is applied to prove that the trays of an opening sewing box must always be parallel.
Quadrilaterals
The document contains information about various properties of quadrilaterals, triangles, and parallelograms. It includes proofs of:
1) The sum of the interior angles of any quadrilateral is 360 degrees.
2) A diagonal of a parallelogram divides it into two congruent triangles.
3) If two triangles are on the same base and between the same parallels, they have equal areas.
Math 8 – triangle congruence, postulates,
The document provides information about triangle congruence, including:
1. There are three postulates for proving triangles are congruent: side-side-side (SSS), side-angle-side (SAS), and angle-side-angle (ASA).
2. The SSS postulate states that if three sides of one triangle are congruent to three sides of a second triangle, then the triangles are congruent.
3. The SAS postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the triangles are congruent.
4. The ASA postulate states that if two angles
Triangle congruence relations aas and sss
This document discusses four methods of showing that triangles are congruent:
1) Angle-Side-Angle (ASA)
2) Side-Angle-Side (SAS)
3) Angle-Angle-Side (AAS)
4) Side-Side-Side (SSS)
It also discusses using the hypotenuse-leg congruence (HL) rule to show right triangles are congruent. The document provides examples of applying each method and encourages practicing identifying the type of congruence shown in different diagrams.
ncert question 10
The document contains solutions to several geometry problems involving properties of parallelograms, triangles, and polygons. It shows that the diagonals of a parallelogram divide it into four triangles of equal area. It also shows that if a diagonal of a quadrilateral bisects a pair of opposite sides, then the quadrilateral is a parallelogram. Finally, it provides a solution to implement a proposal to construct a health center by taking a portion of land from one corner of a landowner's plot and compensating with an equal area of adjoining land.
Basic proportionality theorem
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle, intersecting the other two sides at distinct points, the lengths of the segments of the two sides will be divided in the same ratio. The proof involves drawing additional lines perpendicular to the parallel line and original sides of the triangle, allowing the areas of different triangles to be set equal and proving that the ratios of the corresponding segments are equal.
More Related Content
What's hot
CLASS IX MATHS 6 areas of parallelogram and triangles
The document discusses relationships between the areas of plane figures such as parallelograms, triangles, and rectangles that share the same base or lie between the same parallels. It defines what it means for figures to be on the same base and between the same parallels. The key points are that parallelograms on the same base and between the same parallels have equal areas, and triangles on the same base and between the same parallels also have equal areas. Formulas for calculating the areas of parallelograms and triangles are reviewed.
Geometry 201 unit 4.2
This document provides instruction on proving triangle congruence using the Side-Side-Side (SSS) and Side-Angle-Side (SAS) postulates. It includes examples of using SSS and SAS to show that triangles are congruent, as well as practice problems for students to verify congruence. Key concepts covered are triangle rigidity, included angles, and applying SSS and SAS to real-world geometry problems.
4.2 Congruence and Triangles
Here are 3 practice problems from the textbook:
14. ΔABC ≅ ΔXYZ. Find m∠A if m∠X = 50°.
16. ΔDEF ≅ ΔGHI. If DF = 12 and GH = 8, find IH.
35. Prove: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are congruent.
Similarity of triangles -GEOMETRY
- Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
- There are three criteria for similarity of triangles: AAA (if corresponding angles are equal), SSS (if corresponding sides are proportional), and SAS (if one angle is equal and the sides containing those angles are proportional).
- If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, the triangles on each side of the perpendicular are similar to each other and to the original triangle.
6.6 proportions & similar triangles
This document discusses proportionality theorems and using similar triangles to solve problems involving segment lengths. It provides 6 theorems regarding proportional line segments in triangles and parallel lines cut by transversals. Examples are given to demonstrate using the theorems to find unknown segment lengths. Real-life applications involving building construction are also presented.
Teacher lecture
This document provides an introduction to congruent triangles and the different methods to prove triangles are congruent: SSS, SAS, and ASA. It includes examples of using side and angle correspondences to show triangles are congruent according to the three congruence rules. Students are asked to complete a KWL chart on triangles as an exit ticket.
Module5 dodong2
This document provides instruction and content for a Grade 9 mathematics module on parallelograms. It includes definitions of parallelograms and their properties. Several theorems are proved, including those regarding parallelograms, rectangles, rhombuses, the midline theorem, trapezoids, and kites. Example problems are also provided to demonstrate applying the properties and theorems of parallelograms.
Lecture 4.3
The document discusses congruent triangles and their properties. It defines congruent figures as those with corresponding sides and angles that are congruent. It presents several ways to prove triangles are congruent, including using corresponding parts, vertical angles, the third angle theorem, and properties of congruent figures like the transitive property. It provides examples of writing congruence statements and determining if triangles are congruent based on given information.
Congruent triangles
The document discusses various properties and theorems related to triangles. It begins by defining different types of triangles based on side lengths and angle measures. It then covers the four congruence rules for triangles: SAS, ASA, AAS, and SSS. The document proceeds to prove several theorems about relationships between sides and angles of triangles, such as opposite sides/angles of isosceles triangles being equal, larger sides having greater opposite angles, and the sum of any two angles being greater than the third side. It concludes by proving that the perpendicular from a point to a line is the shortest segment.
7.4 Similarity in right triangles
This document discusses similar right triangles and the geometric mean. It contains examples and theorems about how cutting an altitude to the hypotenuse of a right triangle divides it into two similar right triangles. The geometric mean of two numbers a and b is the positive number x that satisfies ab=x^2. Using the geometric mean and properties of similar triangles, missing side lengths can be calculated.
Right Triangle Similarity
The document discusses similarity in right triangles. It states that drawing an altitude to the hypotenuse of a right triangle divides it into two smaller right triangles that are similar to each other and the original triangle. The altitude also allows one to find missing side lengths using geometric mean formulas. Several examples are given of using these formulas to solve for missing lengths in right triangles.
6.6 use proportionality theorems
This document discusses proportionality theorems and their applications to solving geometry problems involving similar triangles. It provides 4 examples of using proportionality theorems to find unknown side lengths. Specifically, it uses the Triangle Proportionality Theorem, which states that if two triangles are cut by a transversal, then the ratios of the lengths of the corresponding sides are equal. It also uses properties of parallel lines and proportions. The document concludes with guided practice and exit slip problems for students to apply proportionality theorems.
Triangles For Class 10 CBSE NCERT
The document describes how to determine if three lines will form a triangle based on their lengths. It states that if the sum of the lengths of the two shortest lines is less than the longest line, the lines will not form a triangle. If the sum is equal to the longest line, the two shortest lines will overlap the longest line. Only if the sum is greater than the longest line will the three lines form a triangle.
Obj. 19 CPCTC
This document discusses the concept of CPCTC (Corresponding Parts of Congruent Triangles are Congruent). It states that once two triangles are proven to be congruent using SSS, SAS, ASA, AAS, or HL, then all corresponding parts of those triangles are also congruent due to CPCTC. It provides two examples of using CPCTC to prove corresponding angles are congruent after first showing the triangles are congruent using given information.
Cogruence
The document discusses congruence and similarity of triangles and figures. It defines congruence as two figures having equal corresponding sides and angles. Similarity requires proportional corresponding sides and equal corresponding angles. The conditions for congruence of triangles are: side-side-side, side-angle-side, angle-side-angle, and angle-angle-side. Congruence is reflexive, symmetric, and transitive. The conditions for similarity of triangles are: corresponding sides proportional and two or more equal corresponding angles.
Congruence of Triangle
The document discusses different rules for determining if two triangles are congruent, including:
- The ASA (Angle-Side-Angle) rule, which states two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle. An example proof of this rule is provided.
- The SSS (Side-Side-Side) rule, which states two triangles are congruent if three sides of one triangle are equal to the corresponding three sides of the other triangle. An example proof is also provided.
- The Hypotenuse-Leg rule, which states two right triangles are congruent if the hypotenuse and one side of one
Quadrilaterals Theorems
The document contains several theorems about the properties of parallelograms: if a quadrilateral has both pairs of opposite sides congruent, opposite angles congruent, or an angle supplementary to its consecutive angles, then it is a parallelogram. It also proves that if the diagonals of a quadrilateral bisect each other or one pair of opposite sides are congruent and parallel, then it is a parallelogram. This is applied to prove that the trays of an opening sewing box must always be parallel.
Quadrilaterals
The document contains information about various properties of quadrilaterals, triangles, and parallelograms. It includes proofs of:
1) The sum of the interior angles of any quadrilateral is 360 degrees.
2) A diagonal of a parallelogram divides it into two congruent triangles.
3) If two triangles are on the same base and between the same parallels, they have equal areas.
Math 8 – triangle congruence, postulates,
The document provides information about triangle congruence, including:
1. There are three postulates for proving triangles are congruent: side-side-side (SSS), side-angle-side (SAS), and angle-side-angle (ASA).
2. The SSS postulate states that if three sides of one triangle are congruent to three sides of a second triangle, then the triangles are congruent.
3. The SAS postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the triangles are congruent.
4. The ASA postulate states that if two angles
Triangle congruence relations aas and sss
This document discusses four methods of showing that triangles are congruent:
1) Angle-Side-Angle (ASA)
2) Side-Angle-Side (SAS)
3) Angle-Angle-Side (AAS)
4) Side-Side-Side (SSS)
It also discusses using the hypotenuse-leg congruence (HL) rule to show right triangles are congruent. The document provides examples of applying each method and encourages practicing identifying the type of congruence shown in different diagrams.
What's hot (20)
CLASS IX MATHS 6 areas of parallelogram and triangles
CLASS IX MATHS 6 areas of parallelogram and triangles
Similar to TWO TRIANGLES HAVING THE SAME BASE AND EQUAL AREAS LIE BETWEEN THE SAME PARALLELS
ncert question 10
The document contains solutions to several geometry problems involving properties of parallelograms, triangles, and polygons. It shows that the diagonals of a parallelogram divide it into four triangles of equal area. It also shows that if a diagonal of a quadrilateral bisects a pair of opposite sides, then the quadrilateral is a parallelogram. Finally, it provides a solution to implement a proposal to construct a health center by taking a portion of land from one corner of a landowner's plot and compensating with an equal area of adjoining land.
Basic proportionality theorem
The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle, intersecting the other two sides at distinct points, the lengths of the segments of the two sides will be divided in the same ratio. The proof involves drawing additional lines perpendicular to the parallel line and original sides of the triangle, allowing the areas of different triangles to be set equal and proving that the ratios of the corresponding segments are equal.
Triangles class 9
NCERT Solutions of Class 9 chapter 7-Triangles are created here for helping the students of class 9 in helping their preparations for CBSE board exams. All NCERT Solutions of Class 9 of chapter 7-Triangles are solved by an expert of maths in such a way that every student can understand easily without the help of anybody.
congruenttriangles-130611002549-.docx
The document discusses various properties and theorems related to triangles. It defines different types of triangles based on sides and angles. It introduces concepts like congruence of triangles and corresponding parts. It describes the four main congruence rules: SAS, ASA, AAS, and SSS. It also discusses properties like angles opposite to equal sides are equal, sides opposite to equal angles are equal, sum of angles of a triangle is 180 degrees, and theorems related to inequality of sides and angles.
5 similar+triangles%26 power+of+a+point+%28solutions%29
The document contains solutions to 15 exercises involving similar triangles and the power of a point theorem. The exercises cover topics like proving triangles are similar, using the power of a point theorem to solve for lengths and areas, proving properties of radical axes of circles, and showing ways that a quadrilateral can be proven to be cyclic. The solutions provide detailed multi-step workings to prove the statements in each exercise.
Ch 6 TRIANGLES Ex 6.4
This document discusses properties of triangles, including the angle bisector theorem and similarity of triangles. It provides proofs of several geometry theorems related to ratios of sides and areas of similar triangles. Some key points:
- The ratio of corresponding sides of two similar triangles is equal to the ratio of their areas.
- If the ratio of corresponding sides of two triangles is r:s, then the ratio of their areas is r^2:s^2.
- Medians, angle bisectors, and perpendicular bisectors exhibit properties when used to prove similarity.
sagar
The document defines different types of triangles based on their sides and angles. It discusses triangles formed by three non-collinear points connected by line segments. The types of triangles include scalene, isosceles, equilateral, acute, right, and obtuse triangles. Congruence rules for triangles are provided, including SAS, ASA, AAS, SSS, and RHS. Properties of triangles like angles opposite equal sides being equal and sides opposite equal angles being equal are explained. Inequalities relating sides and angles of triangles are described.
ch6.pdf
This document provides solutions to exercises 6.1 through 6.13 from the NCERT Solutions for Class 10 Maths Unit 6 on triangles. The exercises involve applying properties of similar triangles, including corresponding angles criteria, proportional sides criteria, and using basic proportionality theorem to solve for missing lengths. Several multi-part questions prove that various triangles are similar using angle-angle or side-side-side similarity criteria.
#Class 9 #MCQ #Chapter_9 #area_of_paralleograms_and_triangles
This document contains 37 multiple choice questions related to areas of parallelograms and triangles from a Class IX maths learning centre in Jalandhar. Complete video lectures on these topics are available on their YouTube channel. The questions test various concepts like finding the area of parallelograms when dimensions are given, relating the areas of geometric shapes that share bases or are between the same parallels, and determining missing angle measures and side lengths using properties of parallelograms and triangles.
Sol28
1) The figure shows a circle with four points A, B, C, D on the circumference and their incenters X, Y, Z.
2) Similar triangles are used to show that the angles XAY, YDX, YZγ, and δZX are all equal to one-fourth of the arc they intercept.
3) The sum of these four angles is shown to be 90 degrees, implying the quadrilateral formed by the incenters X, Y, Z, W is a rectangle.
Mathematics
1) The document provides information about various types of quadrilaterals including their properties and theorems related to rectangles and parallelograms.
2) Key quadrilaterals discussed include trapezoids, parallelograms, rectangles, squares, rhombus, and kites. Theorems are presented regarding the properties of diagonals and angles of rectangles.
3) Exercises with solutions are provided applying the theorems to problems involving finding angles of quadrilaterals, properties of rectangles and parallelograms, and relationships between sides and angles of figures.
Quadrilaterals
1) A quadrilateral is a geometric figure with four sides, four angles, and two diagonals. The sum of the angles is always 360 degrees.
2) There are six types of quadrilaterals: trapezoid, parallelogram, rectangle, rhombus, square, and kite. A parallelogram has both pairs of opposite sides parallel. A rectangle has one right angle. A square is both a rectangle and rhombus with all sides equal.
3) Theorems include: the diagonals of a parallelogram bisect each other; if the diagonals of a quadrilateral bisect each other it is a parallelogram; a quadrilateral is
midpoint theorem &intersept theorm
This document provides an outline and examples for proving theorems related to midpoints and intercepts in triangles. It includes:
1. Definitions of parallel lines, congruent triangles, and similar triangles.
2. Examples of proofs of the Triangle Midpoint Theorem - which states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long.
3. An example proof of the Triangle Intercept Theorem - which states that if a line is parallel to one side of a triangle, it divides the other two sides proportionally.
Congruent Triangles
The document discusses different theorems for proving triangles are congruent:
- Side-Side-Side (SSS) - If three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent.
- Side-Angle-Side (SAS) - If two sides and the included angle of one triangle are congruent to those of another, the triangles are congruent.
- Angle-Side-Angle (ASA) - If two angles and the included side of one triangle are congruent to those of another, the triangles are congruent.
- Angle-Angle-Side (AAS) - If two angles and the non-included side of one triangle are congr
2sol
1) The document contains 6 multi-step math problems and their solutions.
2) The problems involve concepts like trigonometry, inequalities, divisibility, and proportions in geometric figures.
3) The solutions use techniques like cyclic quadrilaterals, similarity of triangles, and algebraic manipulation of equations.
Circlestangentchordtheorem
This document discusses key concepts in circles such as chords, radii, diameters, tangents, and secants. It presents several important theorems: the Tangent-Chord Theorem states that the angle between a tangent and chord is equal to the inscribed angle on the other side of the chord. The Intersecting Chord Theorem relates the lengths of segments formed by two intersecting chords. The Tangent-Secant Theorem equates the product of a secant and its external segment to the square of the tangent. Examples are provided to demonstrate applications of these theorems.
Midpoit Theorem.pdf
1) The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half its length. This is known as the midpoint theorem.
2) The converse of the midpoint theorem states that a line drawn through the midpoint of one side of a triangle parallel to another side bisects the third side.
3) The theorem on intercepts states that if a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them also makes equal intercepts.
Presentation1
A quadrilateral is a shape with four sides, four angles, and four vertices. There are six types of quadrilaterals: trapezium, parallelogram, rectangle, rhombus, square, and kite. A parallelogram is a quadrilateral where both pairs of opposite sides are parallel. The diagonals of a parallelogram bisect each other and divide the parallelogram into two congruent triangles. Opposite sides and opposite angles of a parallelogram are equal.
Q. In an isosceles triangle ABC with AB = AC, D and E are points on BC such t...
Question based on the theorem:
Angles opposite to equal sides of an isosceles triangle are equal.
Q. In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD. Show that AD = AE.
Similar to TWO TRIANGLES HAVING THE SAME BASE AND EQUAL AREAS LIE BETWEEN THE SAME PARALLELS (20)
5 similar+triangles%26 power+of+a+point+%28solutions%29
5 similar+triangles%26 power+of+a+point+%28solutions%29
#Class 9 #MCQ #Chapter_9 #area_of_paralleograms_and_triangles
#Class 9 #MCQ #Chapter_9 #area_of_paralleograms_and_triangles
Congruence of Triangle 1.pptx Maths, Triangles for GRADE 8
Congruence of Triangle 1.pptx Maths, Triangles for GRADE 8
Q. In an isosceles triangle ABC with AB = AC, D and E are points on BC such t...
Q. In an isosceles triangle ABC with AB = AC, D and E are points on BC such t...
Recently uploaded
Chapter 4 - Islamic Financial Institutions in Malaysia.pptx
Chapter 4 - Islamic Financial Institutions in Malaysia.pptxMohd Adib Abd Muin, Senior Lecturer at Universiti Utara Malaysia
This slide is special for master students (MIBS & MIFB) in UUM. Also useful for readers who are interested in the topic of contemporary Islamic banking.
Azure Interview Questions and Answers PDF By ScholarHat
Azure Interview Questions and Answers PDF By ScholarHat
South African Journal of Science: Writing with integrity workshop (2024)
South African Journal of Science: Writing with integrity workshop (2024)Academy of Science of South Africa
A workshop hosted by the South African Journal of Science aimed at postgraduate students and early career researchers with little or no experience in writing and publishing journal articles.ANATOMY AND BIOMECHANICS OF HIP JOINT.pdf
it describes the bony anatomy including the femoral head , acetabulum, labrum . also discusses the capsule , ligaments . muscle that act on the hip joint and the range of motion are outlined. factors affecting hip joint stability and weight transmission through the joint are summarized.
The simplified electron and muon model, Oscillating Spacetime: The Foundation...
Discover the Simplified Electron and Muon Model: A New Wave-Based Approach to Understanding Particles delves into a groundbreaking theory that presents electrons and muons as rotating soliton waves within oscillating spacetime. Geared towards students, researchers, and science buffs, this book breaks down complex ideas into simple explanations. It covers topics such as electron waves, temporal dynamics, and the implications of this model on particle physics. With clear illustrations and easy-to-follow explanations, readers will gain a new outlook on the universe's fundamental nature.
The History of Stoke Newington Street Names
Presented at the Stoke Newington Literary Festival on 9th June 2024
www.StokeNewingtonHistory.com
A Strategic Approach: GenAI in Education
Artificial Intelligence (AI) technologies such as Generative AI, Image Generators and Large Language Models have had a dramatic impact on teaching, learning and assessment over the past 18 months. The most immediate threat AI posed was to Academic Integrity with Higher Education Institutes (HEIs) focusing their efforts on combating the use of GenAI in assessment. Guidelines were developed for staff and students, policies put in place too. Innovative educators have forged paths in the use of Generative AI for teaching, learning and assessments leading to pockets of transformation springing up across HEIs, often with little or no top-down guidance, support or direction.
This Gasta posits a strategic approach to integrating AI into HEIs to prepare staff, students and the curriculum for an evolving world and workplace. We will highlight the advantages of working with these technologies beyond the realm of teaching, learning and assessment by considering prompt engineering skills, industry impact, curriculum changes, and the need for staff upskilling. In contrast, not engaging strategically with Generative AI poses risks, including falling behind peers, missed opportunities and failing to ensure our graduates remain employable. The rapid evolution of AI technologies necessitates a proactive and strategic approach if we are to remain relevant.
How to Fix the Import Error in the Odoo 17
An import error occurs when a program fails to import a module or library, disrupting its execution. In languages like Python, this issue arises when the specified module cannot be found or accessed, hindering the program's functionality. Resolving import errors is crucial for maintaining smooth software operation and uninterrupted development processes.
How to Manage Your Lost Opportunities in Odoo 17 CRM
Odoo 17 CRM allows us to track why we lose sales opportunities with "Lost Reasons." This helps analyze our sales process and identify areas for improvement. Here's how to configure lost reasons in Odoo 17 CRM
Executive Directors Chat Leveraging AI for Diversity, Equity, and Inclusion
Let’s explore the intersection of technology and equity in the final session of our DEI series. Discover how AI tools, like ChatGPT, can be used to support and enhance your nonprofit's DEI initiatives. Participants will gain insights into practical AI applications and get tips for leveraging technology to advance their DEI goals.
Natural birth techniques - Mrs.Akanksha Trivedi Rama University
Natural birth techniques - Mrs.Akanksha Trivedi Rama UniversityAkanksha trivedi rama nursing college kanpur.
Natural birth techniques are various type such as/ water birth , alexender method, hypnosis, bradley method, lamaze method etcRecently uploaded (20)
Chapter 4 - Islamic Financial Institutions in Malaysia.pptx
Chapter 4 - Islamic Financial Institutions in Malaysia.pptx
Liberal Approach to the Study of Indian Politics.pdf
Liberal Approach to the Study of Indian Politics.pdf
Azure Interview Questions and Answers PDF By ScholarHat
Azure Interview Questions and Answers PDF By ScholarHat
South African Journal of Science: Writing with integrity workshop (2024)
South African Journal of Science: Writing with integrity workshop (2024)
Pride Month Slides 2024 David Douglas School District
Pride Month Slides 2024 David Douglas School District
The simplified electron and muon model, Oscillating Spacetime: The Foundation...
The simplified electron and muon model, Oscillating Spacetime: The Foundation...
How to Manage Your Lost Opportunities in Odoo 17 CRM
How to Manage Your Lost Opportunities in Odoo 17 CRM
Executive Directors Chat Leveraging AI for Diversity, Equity, and Inclusion
Executive Directors Chat Leveraging AI for Diversity, Equity, and Inclusion
Natural birth techniques - Mrs.Akanksha Trivedi Rama University
Natural birth techniques - Mrs.Akanksha Trivedi Rama University
TWO TRIANGLES HAVING THE SAME BASE AND EQUAL AREAS LIE BETWEEN THE SAME PARALLELS
- 2. EXAMPLE- 1
- 3. Show that a median of a triangle divides it into two triangles of equal areas.
- 5. Let ABC be a triangle and let AD be one of its medians suppose, you wish to show area(ABD) = area(ACD) Since the formula for area involves altitude ,let us draw AN┴BC. Now area(ABD) = 1 ∕ 2 x base x altitude(of ∆ADB) = 1 ∕ 2 x BD x AN = 1 ∕ 2 x CD x AN(As BD = CD) = 1 ∕ 2 x base x altitude(of ∆ACD) = area(ACD)
- 6. EXAMPLE- 2
- 7. ABCD is a quadrilateral and BE||AC and also BE meets DC produced at E. Show that area of ∆ADE is equal to the area of the quadrilateral ABCD.
- 9. Solution: In the given figure ∆BAC and ∆EAC lie on the same base AC and between the same parallels AC and BE. Therefore, area(BAC) = area(EAC)(two triangles on the same base and between the same parallels are equal in area) So, area(BAC) +area(ADC) = area(EAC) + area(ADC) (adding same areas on both sides) area(ABCD) = area(ADE)