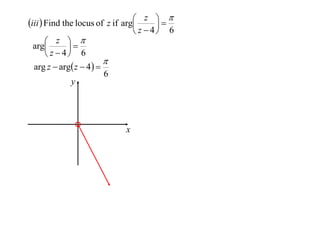
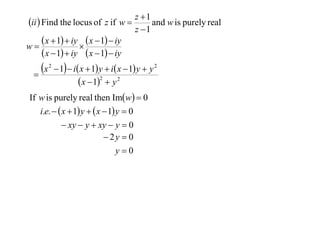The document discusses finding the locus of complex numbers ω or z given some condition on ω or z. It provides examples of determining the locus when: 1) ω is purely real or purely imaginary, which results in the locus being lines. 2) The argument of a linear function of z equals an angle θ, which results in the locus being an arc of a circle. 3) An example is worked through where the locus is a circle with center (1,0) and radius 1/2. 4) Another example finds the locus of z if w is purely real, which results in the locus being the x-axis where y=0.

1. Locus and Complex Numbers

2. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z

3. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)

4. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

5. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

 is purely imaginary  Re   0, arg   
2

6. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

 is purely imaginary  Re   0, arg   
2
 linear function 
arg      locus is an arc of a circle
 linear function 

7. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

 is purely imaginary  Re   0, arg   
2
 linear function 
arg      locus is an arc of a circle
 linear function 

* minor arc if  
2

8. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

 is purely imaginary  Re   0, arg   
2
 linear function 
arg      locus is an arc of a circle
 linear function 

* minor arc if  
2

* major arc if  
2

9. Locus and Complex Numbers
  f  z  , find the locus of  or z
given some condition for  or z
(Make the condition the subject)
 is purely real  Im   0, arg   0 or 

 is purely imaginary  Re   0, arg   
2
 linear function 
arg      locus is an arc of a circle
 linear function 

* minor arc if  
2

* major arc if  
2

* semicircle if  
2

10. z2
e.g .i  Find the locus of w if w  ,z 4
2

11. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2
w
z

12. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2
w
z
zw  z  2

13. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2
w
z
zw  z  2
z w  1  2

14. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2
w
z
zw  z  2
z w  1  2
2
z
w  1

15. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2 2
w  4
z w  1
zw  z  2
z w  1  2
2
z
w  1

16. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2 2
w  4
z w  1
zw  z  2 2
z w  1  2 4
w 1
2
z
w  1

17. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2 2
w  4
z w  1
zw  z  2 2
z w  1  2 4
w 1
2
z w 1 
1
w  1 2

18. z2
e.g .i  Find the locus of w if w  ,z 4
2
z2 2
w  4
z w  1
zw  z  2 2
z w  1  2 4
w 1
2
z w 1 
1
w  1 2
1
 locus is a circle, centre 1,0  and radius
2
1
i.e.  x  1  y 
2 2
4

19. z 1
ii  Find the locus of z if w  and w is purely real
z 1

20. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

21. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2

22. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0

23. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0

24. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0

25. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0

26. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

27. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2
 1  i x  1 y  i x  1 y  y 2
 x  12  y 2
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

28. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

29. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

30. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 -1 1 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

31. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 -1 1 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

32. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 -1 1 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 

33. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 -1 1 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 
locus is y  0, excluding  1,0 

34. z 1
ii  Find the locus of z if w  and w is purely real
z 1
 x  1  iy  x  1  iy OR If w is purely real then arg w  0 or 
w 
 x  1  iy  x  1  iy

x 2  1  i x  1 y  i x  1 y  y 2  z  1   0 or 
i.e. arg 
 x  1  y 2
2  z 1
If w is purely real then Imw  0 arg z  1  arg z  1  0 or 
y
i.e.   x  1 y   x  1 y  0
 xy  y  xy  y  0
 2y  0
y0 -1 1 x
 locus is y  0, excluding 1,0 
 z  1  0, bottom of fraction  0 
locus is y  0, excluding  1,0 
Note : locus is y  0, excluding 1,0  only
i.e. answer the original question

35.  z 
iii  Find the locus of z if arg 
 z  4 6

36.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

37.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

38.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
x

39.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
4x

6

40.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
4x

6
NOTE: arg z  arg z-4 
 below axis

41.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
2
4x

6
NOTE: arg z  arg z-4 
 below axis

42.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
2
r 4x
(2,y)

6
NOTE: arg z  arg z-4 
 below axis

43.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z 

 z  4 6

arg z  arg z  4  
6
y
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

44.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60

 z  4 6 2

arg z  arg z  4  
6
y
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

45.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60

 z  4 6 2
 y  2 tan 60
arg z  arg z  4  
6
y 2 3
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

46.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60

 z  4 6 2
 y  2 tan 60
arg z  arg z  4  
6
y 2 3
 centre is 2,2 3 
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

47.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60 r 2  2 2  2 3 
2

 z  4 6 2
 y  2 tan 60
arg z  arg z  4  
6
y 2 3
 centre is 2,2 3 
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

48.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60 r 2  2 2  2 3 
2

 z  4 6 2
 r 2  16
arg z  arg z  4   y  2 tan 60
6 r4
y 2 3
 centre is 2,2 3 
2
r 4x
(2,y)
30

6
NOTE: arg z  arg z-4 
 below axis

49.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60 r 2  2 2  2 3 
2

 z  4 6 2
 r 2  16
arg z  arg z  4   y  2 tan 60
6 r4
y 2 3
 centre is 2,2 3 
 locus is the major arc of the circle
2
 x  2   y  2 3   16 formed by the
2 2
r 4x
chord joining 0,0  and 4,0  but not
(2,y)
30 including these points.

6
NOTE: arg z  arg z-4 
 below axis

50.  z 
iii  Find the locus of z if arg 
 z  4 6
arg  z  y
 tan 60 r 2  2 2  2 3 
2

 z  4 6 2
 r 2  16
arg z  arg z  4   y  2 tan 60
6 r4
y 2 3
 centre is 2,2 3 
 locus is the major arc of the circle
2
 x  2   y  2 3   16 formed by the
2 2
r 4x
chord joining 0,0  and 4,0  but not
(2,y)
30 including these points.

6 Exercise 4N; 5, 6
Exercise 4O; 3 to 10, 12, 13a, 14, 17,
NOTE: arg z  arg z-4  20b, 21a, 22, 25, 26
 below axis HSC Geometrical Complex Numbers Questions