Ship vibrations can originate from internal or external sources. Internal sources include unbalanced machinery like engines or rotating equipment. External sources include hydrodynamic loads on propellers or slamming forces. The ship responds to excitation forces with both local and hull vibrations. Hull vibrations involve the entire ship and include bending, twisting, and shearing modes similar to a beam. Natural frequencies associated with these modes increase with the number of nodes. 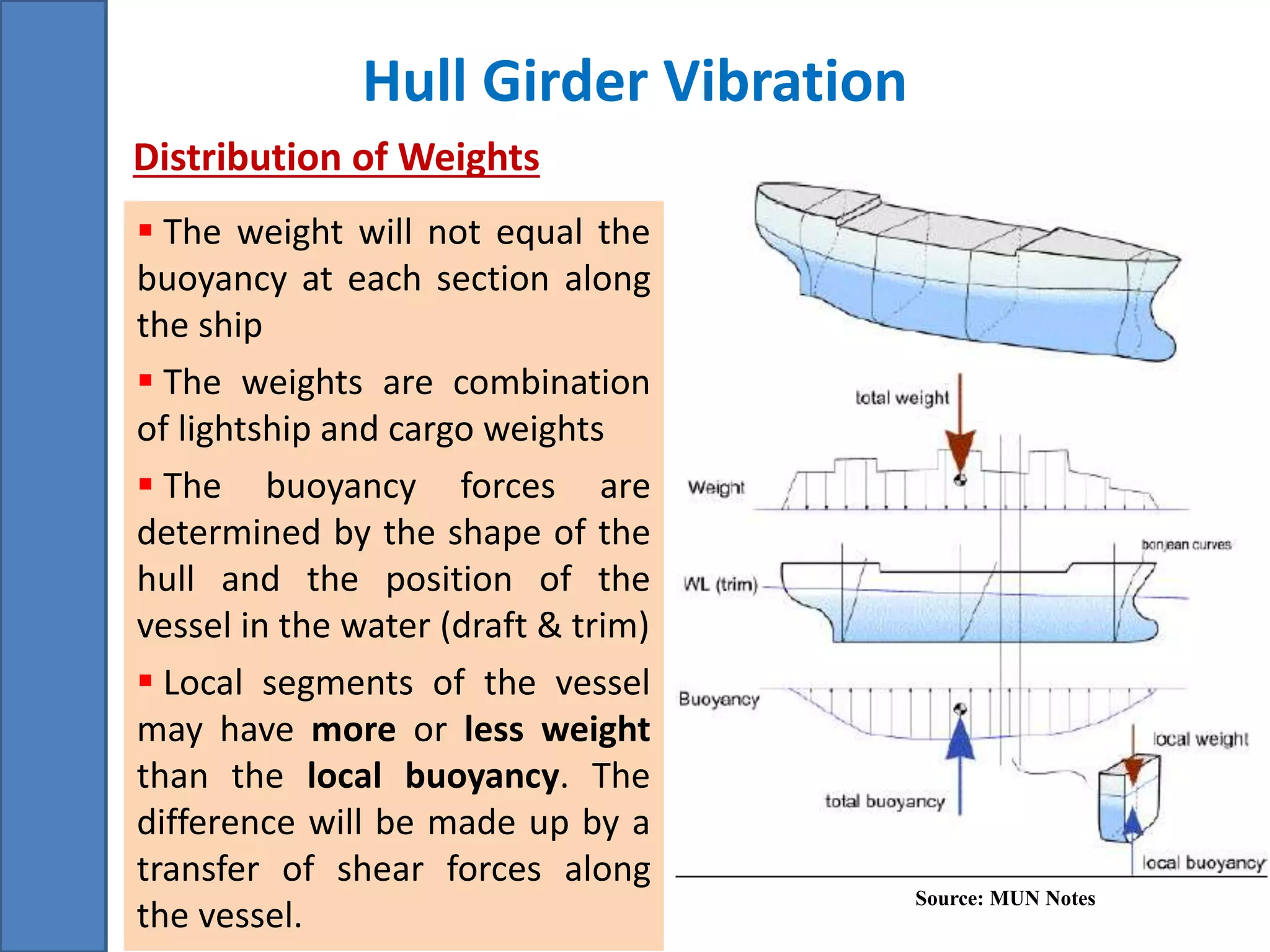To avoid dangerous hull vibrations, exciting forces should be avoided at frequencies close to the ship's natural frequencies, which can be estimated using beam theory formulas involving properties like length, mass, and stiffness.

1. Basics of Ship Vibration

2. Ship Vibration
• SOURCES of SHIP VIBRATION
 Internal Sources [Unbalanced machinery forces]
(1) Main & Auxiliary Machines
• Main Propulsion Engine (esp. 4 or 5 cylinder engine)
generating large unbalanced force at high frequency
close to hull’s natural frequency.
• Rotary Machines (Electric motors, auxiliary machines
etc) generate high frequency but low amplitude
• Reciprocating Engines – Usually low frequency
(2) Unbalanced Shaft ( frequency = shaft RPM)

3. Ship Vibration
• SOURCES of SHIP VIBRATION
 Internal Sources [Unbalanced machinery forces]
UNBALANCE: occurs when centre of mass is different from
centre of rotation. Can be caused by improper assembly,
material buildup, wear, broken or missing parts
Detection: High level radial vibration
MISALIGNMENT: is a condition when two coupled machines
have shafts whose center lines are not parallel and
intersecting, or where one or more bearings are offset or
cocked. Mis-alignment can be caused by improper
assembly and adjustment, foundation failure, thermal
growth, or locked coupling
Detection: High level axial vibration

4. Ship Vibration
• SOURCES of SHIP VIBRATION
 External Sources [Hydrodynamic loading by direct action
or induced by the ship motions]
(1) Hydrodynamic loading on Propellers
Blades in non-uniform flow (freq. = RPM x No. of
blades). More pronounced for low propeller
submergence and in shallow water
(2) Unstable cavitation of blades
(3) Vortex induced forces (not on propeller)
Eg. Brackets that holds the propeller
(4) Slamming Load – short duration forces but give rise to
high frequency forces.

5. Ship Vibration
• SHIP RESPONSE
• In response to excitation forces, the ship execute elastic
vibrations, some of which are observed only locally and some
are observed throughout the hull.
 Local Vibration: Usually high frequency and lower
amplitude
 Difficult to predetermine
 Amended easily post-construction (common practice to
overlook during design stage)
 Hull Vibration: Lower frequency and higher amplitude
(Compared to local)
 Must be carefully considered and avoided in the design
stage itself

6. Hull Girder Vibration
Distribution of Weights
Source: MUN Notes
 The weight will not equal the
buoyancy at each section along
the ship
 The weights are combination
of lightship and cargo weights
 The buoyancy forces are
determined by the shape of the
hull and the position of the
vessel in the water (draft & trim)
 Local segments of the vessel
may have more or less weight
than the local buoyancy. The
difference will be made up by a
transfer of shear forces along
the vessel.

7. Hull Girder Vibration
• SHIP as a UNIFORM BEAM
• Vibrations that exist throughout the hull are of the same type
that may exist in a beam free in space
• Surrounding water plays an important role but it does not
destroy their beamlike characteristic and it is helpful to
consider the vibrations of the ideal solid beam free in space
(free-free beam)
l = 2L
l = L
l = 2L/3
L

8. Hull Girder Vibration
• Types of Elastic Deformation
• A beam free in space can undergo FOUR principal types of
Elastic Deformation:
1) Bending
2) Twisting
3) Shearing
4) Extensional
• Elastic deformations that play a significant role, in the case of
ship are:
 Bending and Shearing in both vertical and horizontal
planes through its longitudinal axis (Flexural)
 Torsion about the longitudinal axis (Twist)

9. Hull Girder Vibration
• Types of Elastic Deformation
 Flexural: Bending like a beam
 Horizontal bending mode
 Vertical bending mode (usually more of a concern than
the horizontal mode)
Torsional: Twist of a beam
 More likely for container ships

10. Hull Girder Vibration
• MODES and NODES
• Mode: the pattern or configuration (shape) which the body
assumes periodically while in vibratory conditions
• Node: is a point in the body which has no displacement when
the vibration is confined to one particular mode.
• Normal Modes: are patterns in which the body can vibrate
freely after the removal of external forces
Connecting nodes,
give corresponding
mode

11. Hull Girder Vibration
 In both Flexural and Torsional vibrations, a natural
frequency is associated with each pattern of vibration and
the natural frequencies increase as the number of nodes
(points at which curves cross x-axis).
 If a free-free beam is unsymmetric w.r.t either the vertical
or horizontal planes through its longitudinal axis, it will be
found that the natural modes of vibration involve Torsion,
Bending and Shearing simultaneously.

12. Hull Girder Vibration
A hull is much more complicated structure than a solid beam
and therefore it behaves like the free-free beam ONLY in its
lower modes of vibration.
These are called beam-like modes and may be excited by
either:
(a) Transient disturbances (due to wave or slamming
impact)
(b) Steady-state disturbances (rotating unbalanced engine
or machine elements, unbalanced propellers,
unbalanced shaftings)

13. Hull Girder Vibration
How to avoid dangerous vibrations of the ship’s hull?
 Avoid exciting forces at frequencies close to the natural
frequencies of the ship’s hull.
How to determine the natural frequencies of the hull
girder?
 Basic concepts are developed from the simple notions of a
uniform beam vibration.
 It’s then extended to the vibration of a ship with some
more added complexities that would reflect the realities of a
ship in the way that a ship differs from a uniform beam
Natural Frequency of Hull Girder

14. Hull Girder Vibration
Minimum number of nodes = 2
Fundamental Mode of Flexural Vibration
Frequency (in cpm) corresponding to this 2 noded vertical
vibration (fundamental mode) is denoted by N2V or NV2
(number of cycles per minute in 2-noded vertical vibration)
Otto Schlick:
32
L
I
N V

 
I = Imidship of the cross-section of the ship (beam)
 = Weight displacement of the ship (beam)
L = Length of the ship (beam)

15. Z
X
q (x, t)
q – the driving force / unit length
in the z-direction
Hull Girder Vibration
Uniform Beam Vibration Equation
Just as a S-DOF system provides basis for understanding
vibrating characteristics of many mechanical systems, similarly,
a uniform FREE-FREE BEAM provides the basis for
understanding the essential vibratory characteristics of ship.
 Free-Free Beam is a continuous system
 Beam is assume to have a mass/unit length,  = A and
Bending stiffness – EI in x-z plane
 BM due to normal internal stresses acting at any cross-section
is related to the mean radius of curvature
;
R
EI
M  R – radius of curvature

16. Hull Girder Vibration
Uniform Beam Vibration Equation
M
dx
zd
EI 2
2
For small deflections in z-direction, the approximation that
curvature (1/R) is equal to 2nd derivative of z w.r.t x can be used
2
2
dx
zd
EIM 
The Euler-Bernoulli equation describing the relationship
between beams deflection and the applied load
OR
q
dx
zd
EI
dx
d






2
2
2 )(4
4
xq
dx
zd
EI OR
Equation relating BM and deflection in simple beam theory.

17. Hull Girder Vibration
Uniform Beam Vibration Equation
Inertia effect of surrounding water
 The relative high density of water makes the inertial effect
a serious concern
 Apparent increase in mass of a body vibrating in water
),(4
4
2
2
txq
x
z
EI
t
z
A 






Inertia
effect
Restoring force as a
result of elasticity
Loading on
the beam