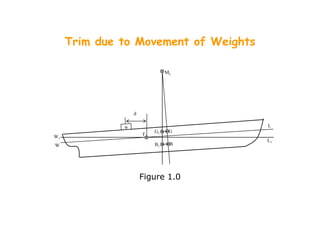
This document discusses longitudinal stability and trim in ships. It defines key terms like trim, longitudinal center of flotation, trimming moment, and moment to change trim. It describes how trim occurs when the forward and aft drafts are unequal and explains how small weight changes affect trim. Weight shifts produce a trimming moment that changes the trim according to the trimming moment divided by the moment to change trim. The changes in forward and aft draft are then calculated based on the new trim.

1. SMALL ANGLE STABILITY:
Longitudinal Stability

2. INTRODUCTION
• In the previous section, we have calculated vertical and
transverse weight shifts, weight additions, and weight
removals. In this section we will look at longitudinal weight
shifts, weight additions, and weight removals. Longitudinal
problems are done in a different manner because we are
usually not concerned with the final position of G, but the
new trim condition of the ship.
• The consequence of longitudinal shifts, additions, and
removals of weight is that the ship undergoes a change in
the forward and after drafts. When the forward and after
drafts have different magnitudes the ship is said to have
trim.
• Trim is defined by the difference between the forward and
after drafts.
Trim = Taft - Tfwd

3. INTRODUCTION Cont.
• If a ship is "trimmed by the bow," then the forward draft is
bigger than the after draft. A ship "trimmed by the stern"
has an after draft bigger than the forward draft.
•• Recall that the ship rotates about the center of flotation (F)
which is the centroid of the waterplane area. (It does not
rotate about midships!) When the centroid of the
waterplane area is aft of midships the forward draft will
change by a larger amount than the after draft. This is
usually the case since a typical ship is wider aft of midships
than forward of midships.

4. LONGITUDINAL STABILITY AND TRIM
• A ship floating at equal draught all along is said to be on an
even keel, or to have zero trim. If the draughts are not the
same from bow to stern, the ship is floting with a trim.

5. LONGITUDINAL STABILITY AND TRIM
Cont.
• Two waterlines (or waterplanes) are shown on the ship in
Figure 1.0; a trimmed waterline (W1L1) and the even keel
waterline (WL) corresponding to the same displacement.
They are shown intersecting at the centre of flotation of the
even keel waterplane. The quantities shown in the figure
are defined as follows:
• Centre of Flotation (F): Geometric center of the ship's
waterline plane. The ship trims about this point. May be
forward or aft of the midships depending on the ship's hull
shape at the waterline.
•• Longitudinal Centre of Flotation (LCF) : Distance from
the centre of flotation (F) to the midships. Used to
distribute changes of trim between the fwd and aft
draughts.

6. LONGITUDINAL STABILITY AND TRIM
Cont.
• Trim (t) : The difference between the forward and after
draughts
• Parallel Rise/Sinkage (PR/PS): When weight is
removed/added from/to a ship at LCF, the forward and aft
drafts will change by the same amount. Means, no trim
occur.
•• Change in Trim (CT): The sum total of the absolute
values of the change in forward and after drafts.
• Trimming Arm (d): The distance from the center of
gravity of the weight to the LCF. If the weight is shifted, (d)
is the distance shifted.

7. LONGITUDINAL STABILITY AND TRIM
Cont.
• Trimming Moment (TM): Moment about the LCF
produced by weight additions, removals, or shifts (wd),
where w is the amount of weight added, removed, or
shifted.
• Moment to change Trim One cm (MCTC): The moment
necessary to produce a change in trim (CT) of one cm.
Found using the hydrostatic curves.
• Tons Per cm Immersion (TPC): The number of tons
added or removed necessary to produce a change in mean
draft (parallel sinkage) of one cm. Parallel sinkage is when
the ship changes it’s forward and after drafts by the same
amount so that no change in trim occurs.

8. LONGITUDINAL STABILITY AND TRIM
Cont.
•TF : Draught forward
•TA : Draught aft
•TM : Mean draught at amidships. It is the average of TF and TA.
••TO : Draught at centre of floation, also called the corresponding
even keel draught.
•δTF : Change in draughts forward
•δTA : Change in draughts after
• θθ: trim angle
Figure 2.0 shows more detail on hull geometry and sign conventions adopted in this notes

9. Figure 2.0

10. Trim due to Movement of Weights
ML
L
d
w
F G1 G W1 L
B1 B
1
W
L1
Figure 1.0

11. Trim due to Movement of Weights
Cont……
• Consider the ship as in Figure 1.0 above, if the weight w is
moved a distance d meter, G will move to G’’ parallel to the
direction of movement of w.
w× ×
d
Δ
GG'= w • The shift in weight results in a trimming moment wd and the
ship will trim until G and B are in line. LCF, the centre of
floatation is the centre of area of the water plane. For small trim,
the ship is assumed to be trimming about LCF. The trimming
moment causes change in trim and hence change in draughts at
AP and FP.

12. Trim due to Movement of Weights
Cont……
• Change in trim (CT),
Change in trim(CT ) = trimming moment
MCTC
• Changes in draught forward, δTF and aft, δTA can be obtained
by dividing trim in proportion to the distance from LCF to the
y g p p
positions where the draughts are measured, normally AP and FP.

13. Trim due to Movement of Weights
Cont……
Amidship
δTA x
F
δTF
T
Trim
T
TA
TF
LBP
Baseline

14. Trim due to Movement of Weights
Cont……
• Trim is defined as the difference in the draughts aft and
forward.
F A TF TA t = T −T =δ +δ
• The angle of trim may be expressed as follows
δ tan = t = TF δ
= TA
LBP LBP LBP
θ
+ LCF − LCF
2 2

15. Trim due to Movement of Weights
Cont……
• Change in draughts forward
⎟
⎟ ⎟ ⎞
⎜ ⎜ ⎜ ⎛
LBP +
LCF
δ = ×
2
LBP
t TF
Ch i d ht ft
⎟ ⎠
⎜
⎝
⎜
• Change in draughts after
⎟ ⎟ ⎞
⎜ ⎜ ⎛
LBP − LCF
2
⎟ ⎟ ⎠
⎜
⎝
⎜ ⎜
= ×
LBP
t TA
δ

16. Small Weight Changes
• If a small weight w is added or removed from a ship, the
draught of the ship will change as follows:
w
TPC
Parallel sinkage / rise = Change in trim (CT) trimming moment (TM) w× distance to
LCF
MCTC
= =
MCTC
• Once the trim is obtained, the changes δTF and δTA can be
calculated and the final draughts will include the parallel
rise/sinkage and δδTF and δδTA.

17. Exercise 1
• A ship LBP 100m has MCTC 125 tonne.m while its LCF
is 2.0 m aft of amidships. Its original draughts are 4.5 m
at AP and 4.45 m at FP. Find new draughts when a 100
tonne weight already on board is moved 50 m aft.

18. Exercise 2
• A ship LBP 100 m has LCF 3 m aft of amidships and
floats at 3.2 m and 4.4 m at FP and AP respectively. Its
TPC is 10 tonne while MCTC 100 tonne.m. 50 tonne
cargo is removed from 20 m forward of amidships while
30 tonne is unloaded from cargo hold 15 m aft of
amidships. Find the final draughts at the perpendiculars.