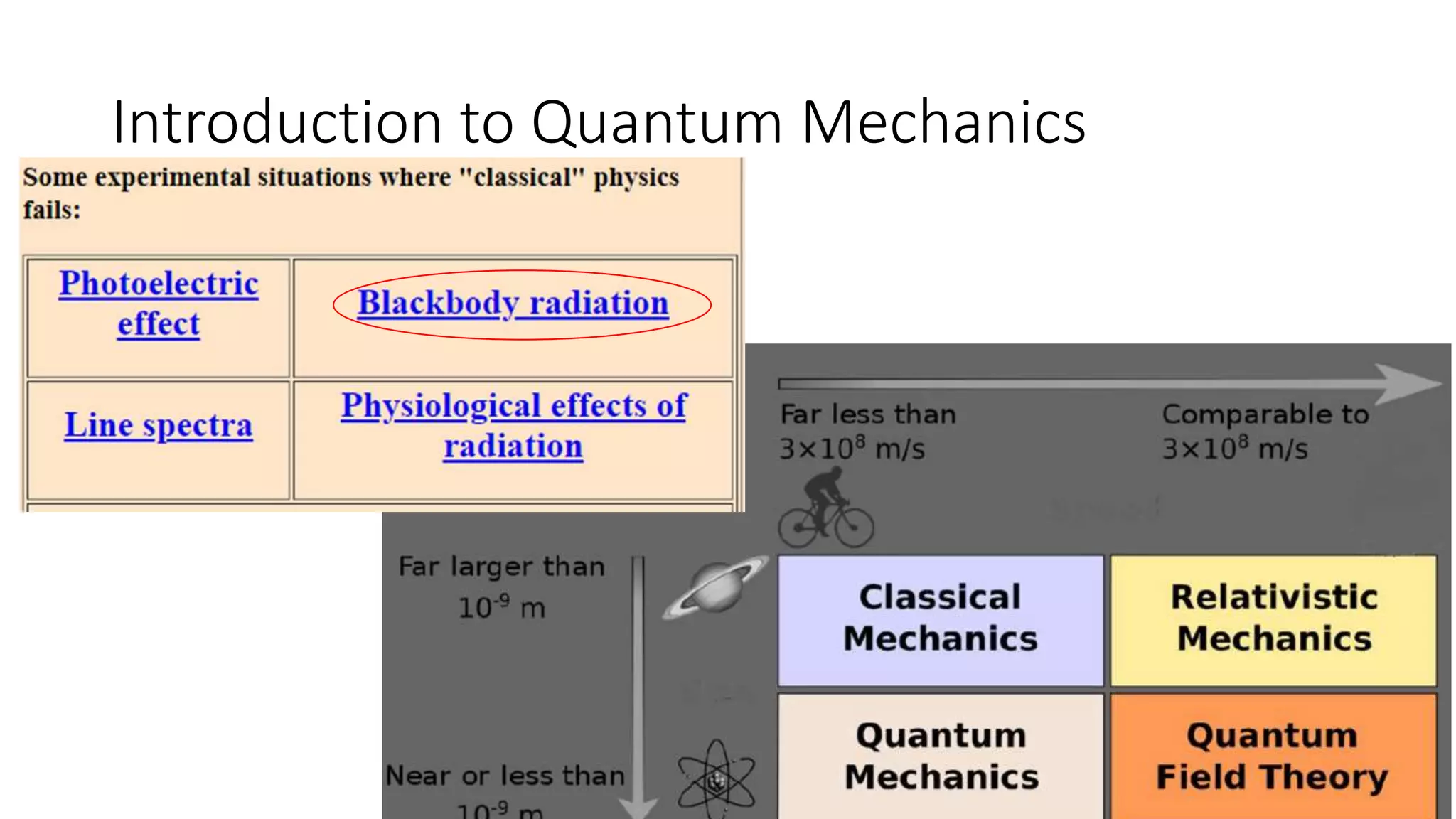
This document provides an introduction to quantum mechanics concepts including: - Quantum mechanics describes nature at small scales where classical physics is insufficient. Pioneers who established the foundations of quantum mechanics are mentioned. - Key concepts are introduced such as wave-particle duality, matter waves, Heisenberg's uncertainty principle and its application to electrons not existing in atomic nuclei. 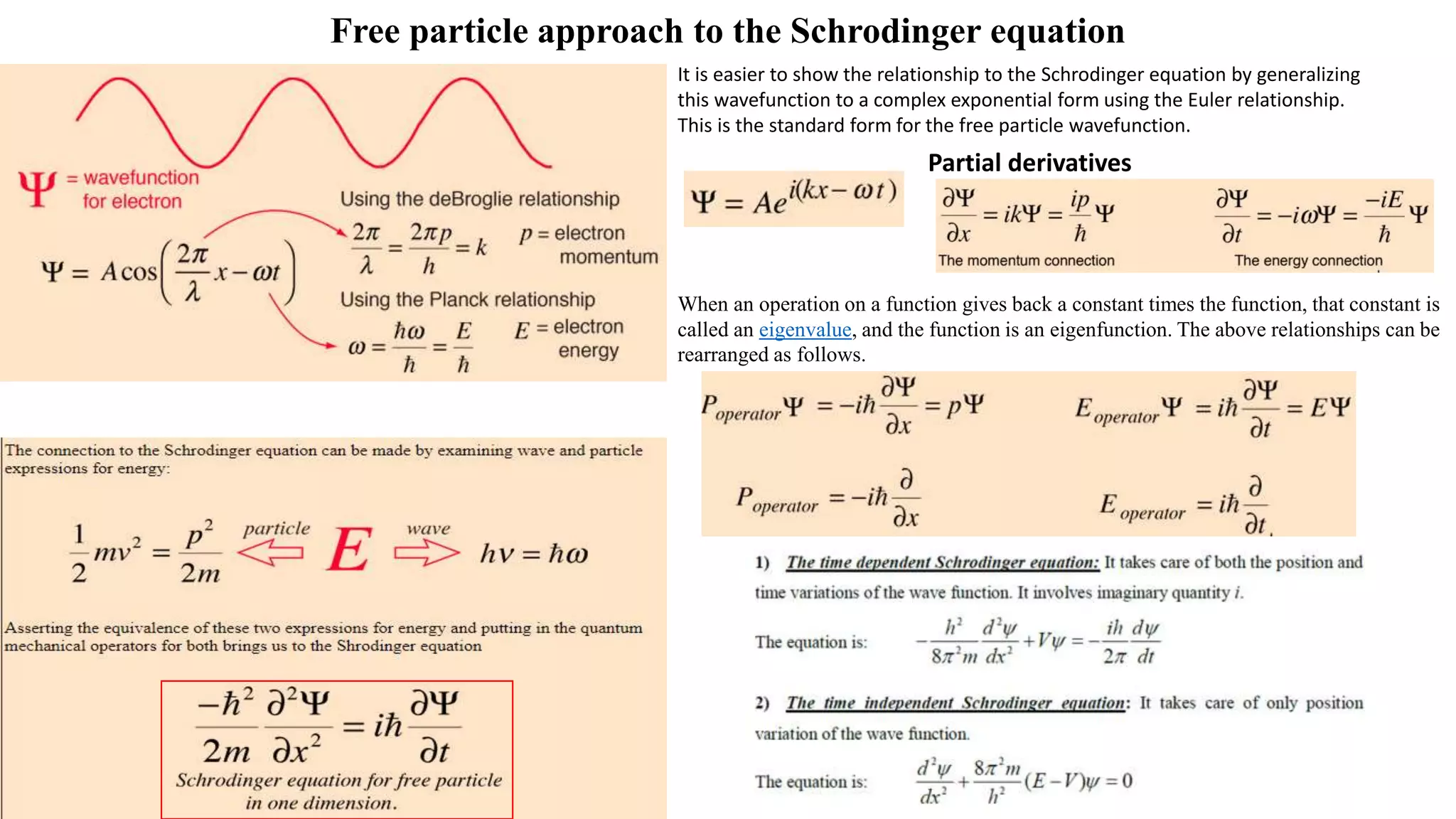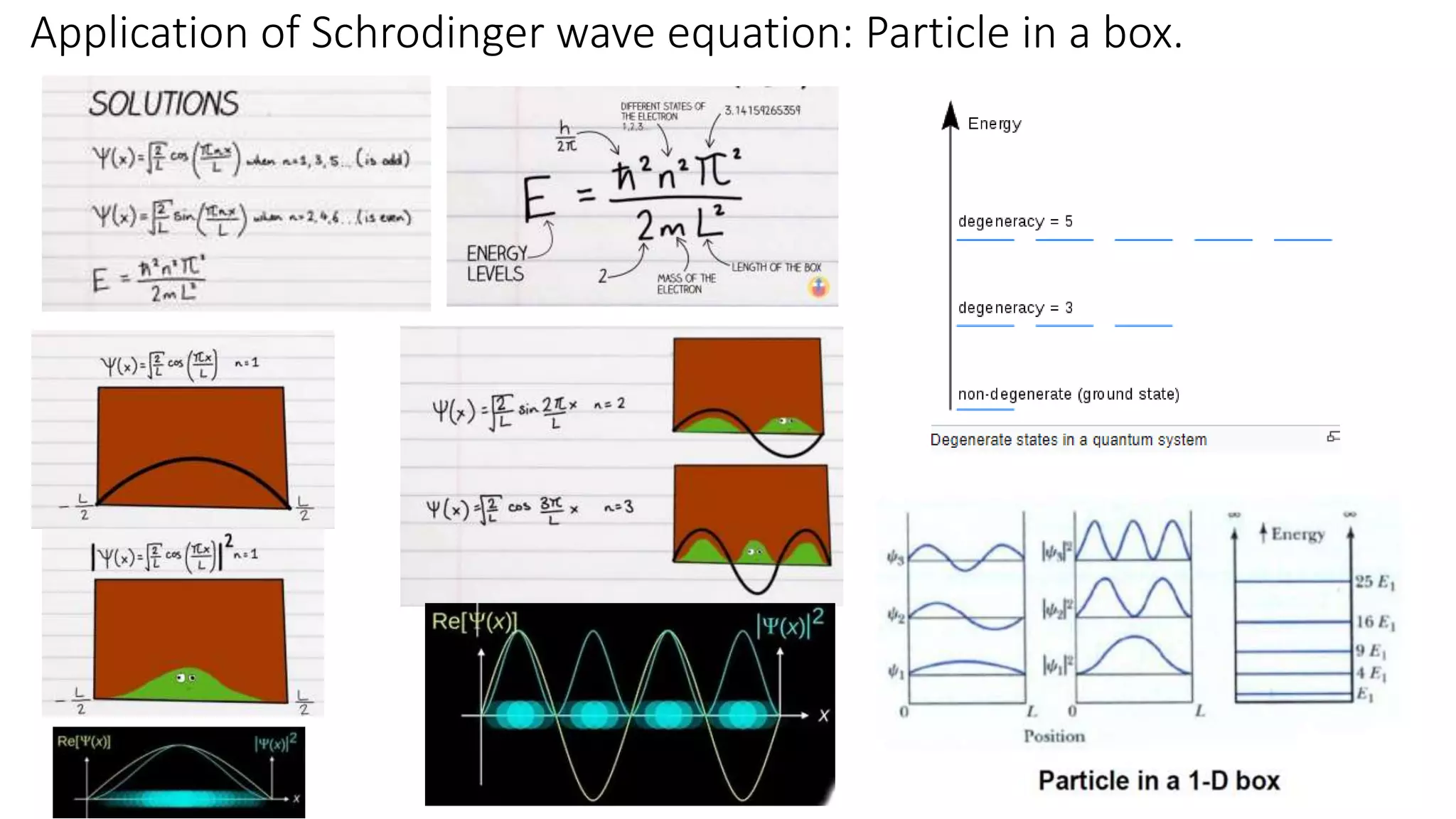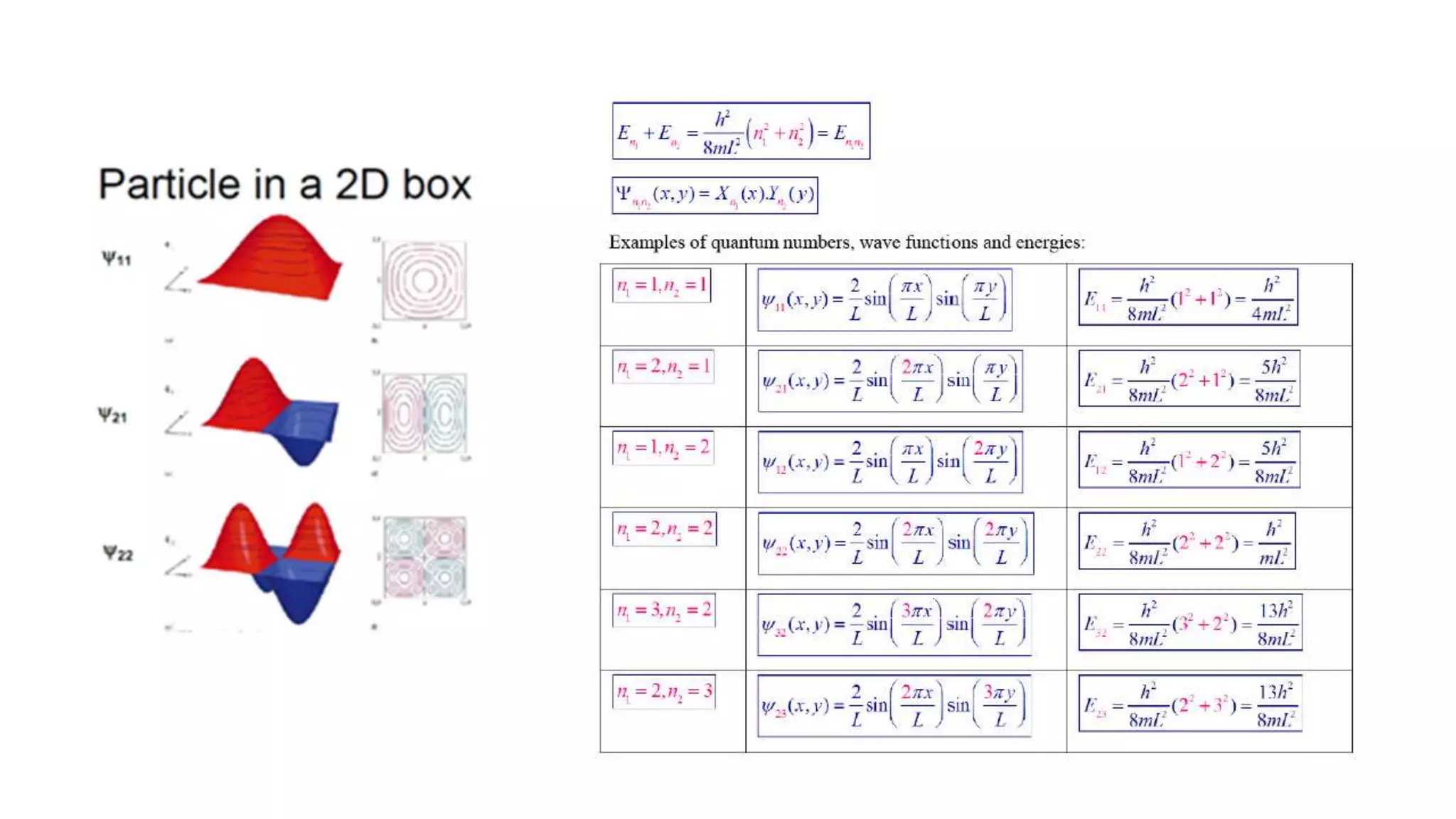- The Schrodinger wave equation is derived and applied to problems such as a particle in an infinite potential well to solve for energy eigenstates and eigenvalues.

1. I&II Semester -2020-21
Engineering Physics
Unit-2. Quantum Mechanics:
By
Hasan Ziauddin
Assistant Professor
Department of Physics
RIET , Jaipur
Rajasthan

2. Introduction to quantum Mechanics
• It describes advanced properties of nature on an atomic scale.
• Classical physics, the description of physics that existed before the theory of
relativity and quantum mechanics, describes many aspects of nature at an
ordinary (macroscopic) scale, while quantum mechanics explains the aspects of
nature at small (atomic and subatomic) scales, for which classical mechanics is
insufficient.
• The foundations of quantum mechanics were established during the first half of
the 20th century by Max Planck, Niels Bohr, Werner Heisenberg, Louis de Broglie,
Arthur Compton, Albert Einstein, Erwin Schrödinger, Max Born, John von
Neumann, Paul Dirac, Enrico Fermi, Wolfgang Pauli, Max von Laue, Freeman
Dyson, David Hilbert, Wilhelm Wien, Satyendra Nath Bose, Arnold Sommerfeld,
and others

3. Modern Physics and Quantum Mechanics
Black body radiation spectrum, Assumptions of quantum theory of radiation,
Plank‟s law, Weins law and Rayleigh Jeans law, for shorter and longer wavelength
limits. Wave Particle dualism, de Broglie hypothesis. Compton Effect and its
Physical significance. Matter waves and their Characteristic properties, Phase
velocity and group velocity. Relation between phase velocity and group velocity,
Relation between group velocity and particle velocity.
Heisenberg‟s uncertainty principle and its application, (Non-existence of electron
in nucleus). Wave function, Properties and physical significance of wave function,
Probability density and Normalization of wave function. Setting up of one
dimensional time independent Schrodinger wave equation. Eigen values and Eigen
functions. Application of Schrodinger wave equation. Energy Eigen values and
Eigen functions for a particle in a potential well of infinite depth and for free
particle.

4. Introduction to Quantum Mechanics

5. Wave-particle duality, Matter waves
Does All Matter Exhibit Wave-like Properties???????
De Broglie Hypothesis: All matter exhibits wave-like properties and relates the observed
wavelength of matter to its momentum. All material particles in motion shows a wave character
these waves are called “Matter Waves” or “De Broglie Waves”

6. Experimental Verification of Matter Waves
(Davisson and Germer Expeiment)
It was noticed that a strong peak appeared in the intensity I of the scattered electrons for an accelerating voltage was of 54 V at a
scattering angle θ=50 . The appearance of the peak in a particular direction is due to the constructive interference from different
layers of the regularly spaced atoms of the crystal.
Electron diffraction experiments carried out by
Davisson and Germer, in 1927 and by G.P
Thompson, in 1928, who observed diffraction
effects with beams of electrons scattered by
crystals. A schematic arrangement of the
experimental arrangement is as shown in the
figure.

7. Characteristics of matter waves

8. The Uncertainty Principle (“The determination of exact position and momentum of a moving particle
simultaneously is impossible”)
• The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision.
There is a minimum for the product of the uncertainties of these two measurements. There is likewise a minimum
for the product of the uncertainties of the energy and time.
• When you say that the electron acts as a wave, then the wave is the quantum mechanical wavefunction and it is
therefore related to the probability of finding the electron at any point in space. A perfect sinewave for the
electron wave spreads that probability throughout all of space, and the "position" of the electron is completely
uncertain.
Application of Uncertainty Principle:
Impossibility of existence of electrons in the atomic nucleus

9. Wave function
Schrodinger suggested to
find probability instead of
exact position

10. Probability Function

11. Probability of finding electron near nucleus

12. Probability can never
be negative, least value
could 0 therefore
square of wavefunction
is calculated to find
probability of exitance
of the particle

13. Wave Equation

14. Postulate

16. Constraints on Wavefunction

17. Probability & Normalization in Quantum Mechanics
The probability of finding a particle
having wave function „ψ‟ in a
volume „dr‟ is „|ψ|²dr‟. If it is
certain that the particle is present in
finite volume „r‟, then
Assignment:
(Orthogonalization)
(Normalization)

18. Schrodinger Equation

19. Free particle approach to the Schrodinger equation
It is easier to show the relationship to the Schrodinger equation by generalizing
this wavefunction to a complex exponential form using the Euler relationship.
This is the standard form for the free particle wavefunction.
Partial derivatives
When an operation on a function gives back a constant times the function, that constant is
called an eigenvalue, and the function is an eigenfunction. The above relationships can be
rearranged as follows.

20. Schrodinger time independent wave equation:

21. Wave function
Where are e likely to be
Energies the e is
Allowed to have
Potential Energy
Kinetic Energy

22. Application of Schrodinger wave equation: Particle in a box.