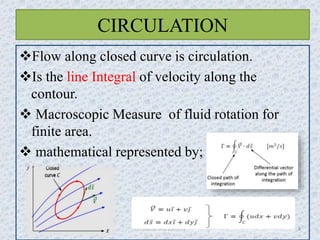
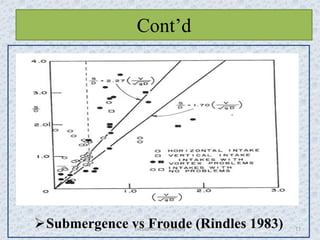
This presentation discusses circulation and vorticity in fluid dynamics. It defines circulation and vorticity, describes their mathematical representations, and how vorticity forms. It examines forced and free vortices, and classifies vortices according to their effects. The presentation also explores how vortices impact hydraulic structures like dams and how to suppress vortices, and includes MATLAB code examples and videos to demonstrate circulation and vorticity concepts.

1. Addis Ababa University
Addis Ababa Institute of Technology
School of Civil and Environmental Engineering
Hydraulic Engineering(Msc)
Course :Hydrodynamics (CEng-6601)
Presentation Title : Circulations and Vorticity
Prepared by : Dereje Fituma
ID:GSR/7847/11
Instructor; Dr. Daneal F.Sillassie
1

2. Presentation Outline
Introduction
Circulation and Vorticity
Mathematical Representations
 Formation and Effects of Vorticity
Mat Lab expression of Circulation & Vorticity
Video Support
2circulation and vorticity

3. INTRODUCTION
Flow visualization is the vital tool for
understanding and development in fluid
Dynamics.
To Examine Formation , Representation and
Application of fluid particles patterns.
Circulation and vorticity are the two primary
measure of fluid rotation.
3

4. CIRCULATION
Flow along closed curve is circulation.
Is the line Integral of velocity along the
contour.
 Macroscopic Measure of fluid rotation for
finite area.
 mathematical represented by;
4circulation and vorticity

5. The tendency of fluid particle to spin about axis.
Microscopic measure of rotation of at any point
in the flied.
Circulation per unit of enclosed area .
 The curl of velocity vector.
 unit rad/sec.
5circulation and vorticity
Vorticity

6.  Stoke’s theorem: velocity V should be defined
properly and continuously differentiable over
the area A.
For 2D flow in x,y plane :
6circulation and vorticity
Circulation and Vorticity

7.  Inviscid ,incompressible ,irrotational flow
governed by Laplace's Equation.
The velocity potential and stream function for
the free vortex are commonly expressed in
terms of circulation .
When velocity distributions are
7circulation and vorticity
Vortex and Potential flow

8. Formation of Vortex
Occurs when flow transition from open
channel flow to pressure flow is not uniform
and smooth .
Observed by natural phenomena such a
tornados, swirling flow of river ,smoke ring,
when modification to flow patterns by wind
,ice ,wave and debris material.
8

9. Forced (irrotational )vortex
Fluid mass is rotating due to some external
source of power.
There is constant torque which rotate the fluid
mass with constant angular velocity
Vortex line: a line that point in the direction of the
vortex vector.
Vortex tube: a bundle of vortex lines
9
circulation and vorticity
Type of Vortex

10. 10
circulation and vorticity
Cont’d…
Forced vortex Free vortex

11.  When a fluid mass rotates with out any external
forces.
 No expenditure energy from external forces .
Tangential velocity inversely proportional to
radius.
Examples: whirlpool in river.
Flow around a circular in bend pipes system.
 Wash basin ,bath tub ,drainage at bottom outlet.
11circulation and vorticity
FREE VORTEX

12. 12circulation and vorticity
Vortex Class
 According to Sarkandeh et al (2010) vortex
classified into three classes; class A,B &C.
 Class C: safe vortex.
 weak rotation flow & small drop observed.
Class B; vortex intended down to the intake
structure.
Drag debris or trash in to intake.
Class A:dangerous vortex should be avoided.
air bubbles are entertained from water surfaces .

13. 13circulation and vorticity
Vortex Effects
Intake of Hydropower Plant
Dams and Reservoir
Vibrations
Efficiency loss: by inducing air and trash into
tunnel.
Flow Reduction
Damage Structures
Loss of Revenues
Cavitation
Etc.

14.  Dissipate the angular momentum of flow
Increasing outlet area: decrease intake velocity
Providing anti vortex wall
Design intake at critical submergence depth
 Using Covered intake type.
Providing trash rack
14circulation and vorticity
Vortex Suppressor

15. 15circulation and vorticity
Cont’d ..

16. Cont’d
16
Parameters effects vortex :
Intake submergence depth
Intake velocity
Intake Froude number
Bulk circulation of fluid

17. Submergence vs Froude (Rindles 1983) 17circulation and vorticity
Cont’d

18. 18
Mat lab & Video Support

19. Vortex code
• % this is vortex flow
• % vortex= phi=-K/2*pi*ln(r)
• [x ,y]=meshgrid(-4:0.1:4);
• k=2;
• Z=-k/(2*pi)*log(sqrt(x.^2+y.^2));
• contour(Z,[-4:0.1:4]);
• xlabel('x');
• ylabel('y');
• title('vortex flow') 19

20. Vortex & uniform flow code
• % this is vortex flow with uniform flow
• % vortex= phi=-K/2pi*ln(r)+uy
• [x ,y]= meshgrid(-3:0.2:3);
• K= 6;
• u=1;
• Z=-K/(2*pi)*log(sqrt(x.^2+y.^2))+u*y;
• contour(Z,[-3:0.2:3]);
• xlabel('x');
• ylabel('y');
• title('Vortex & Uniform Flow')
20

21. 21