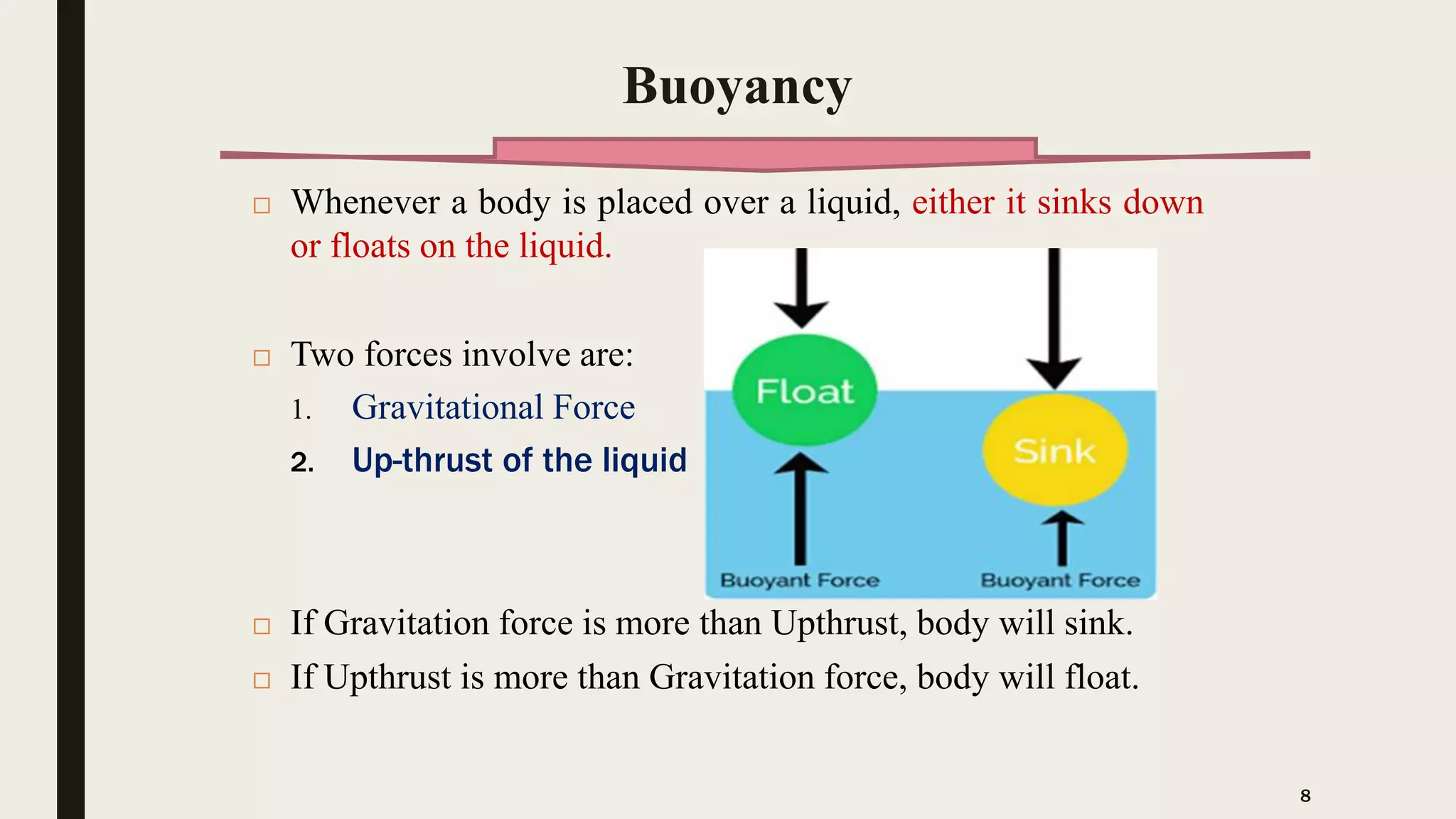
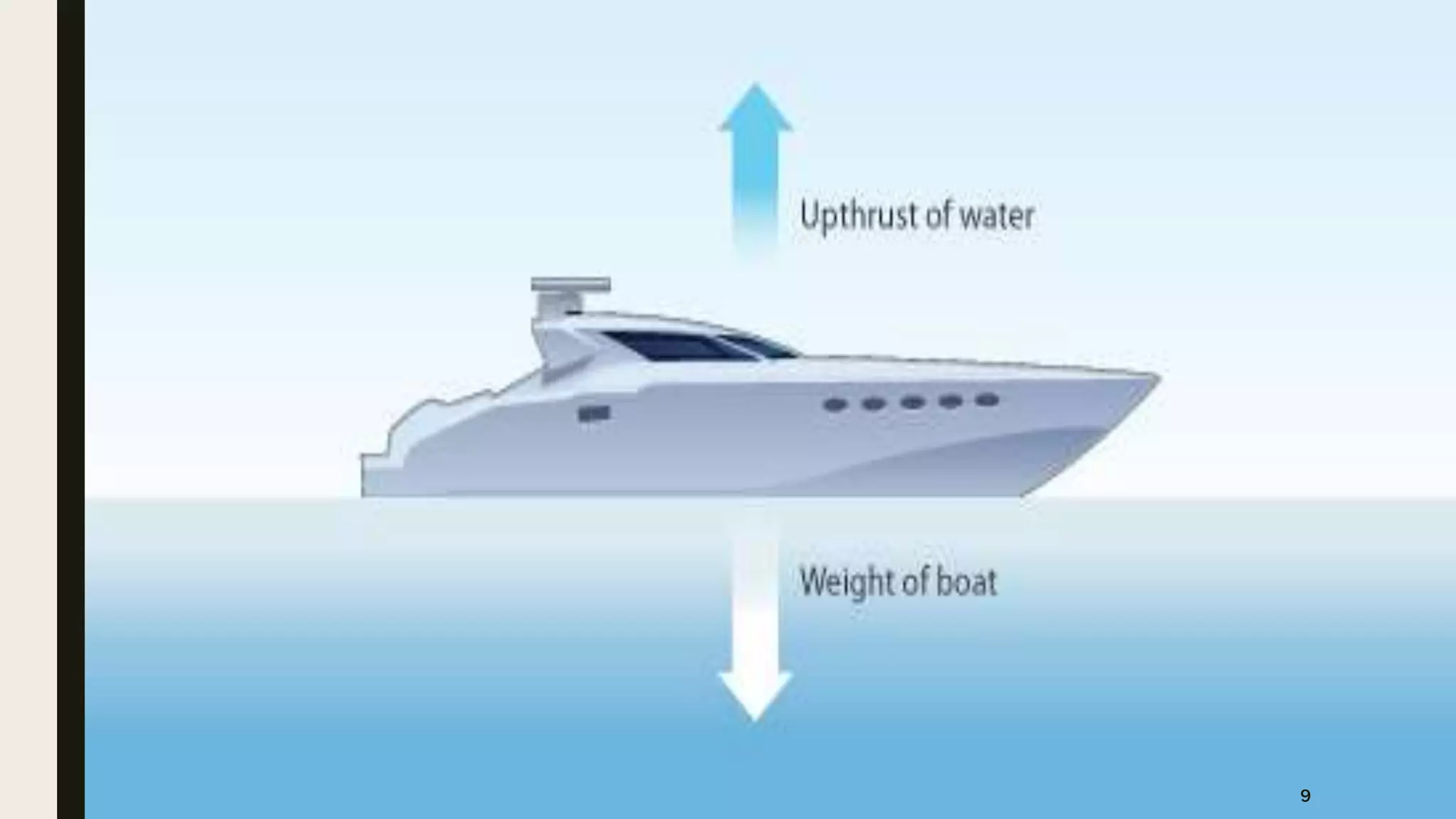
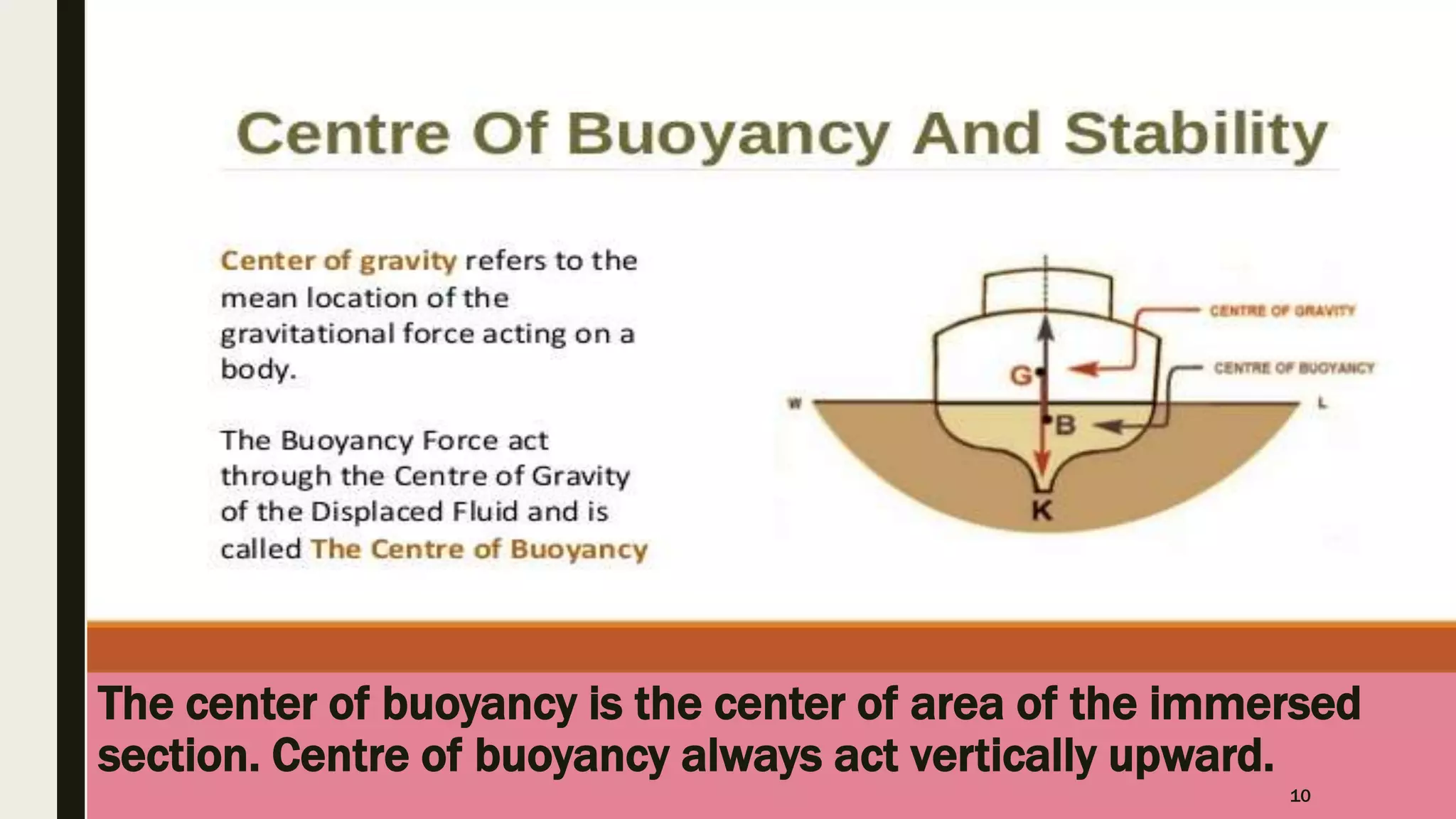
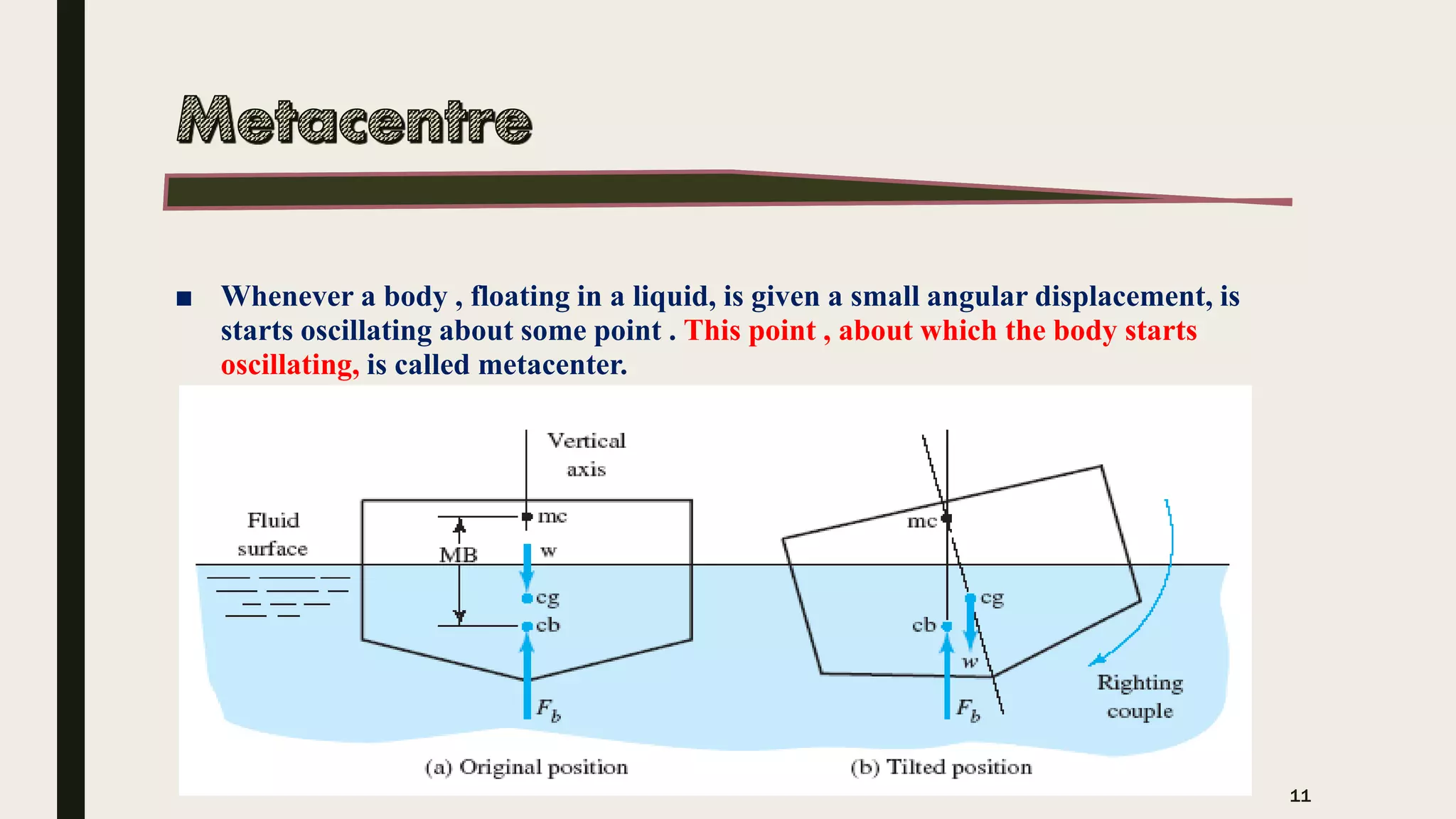
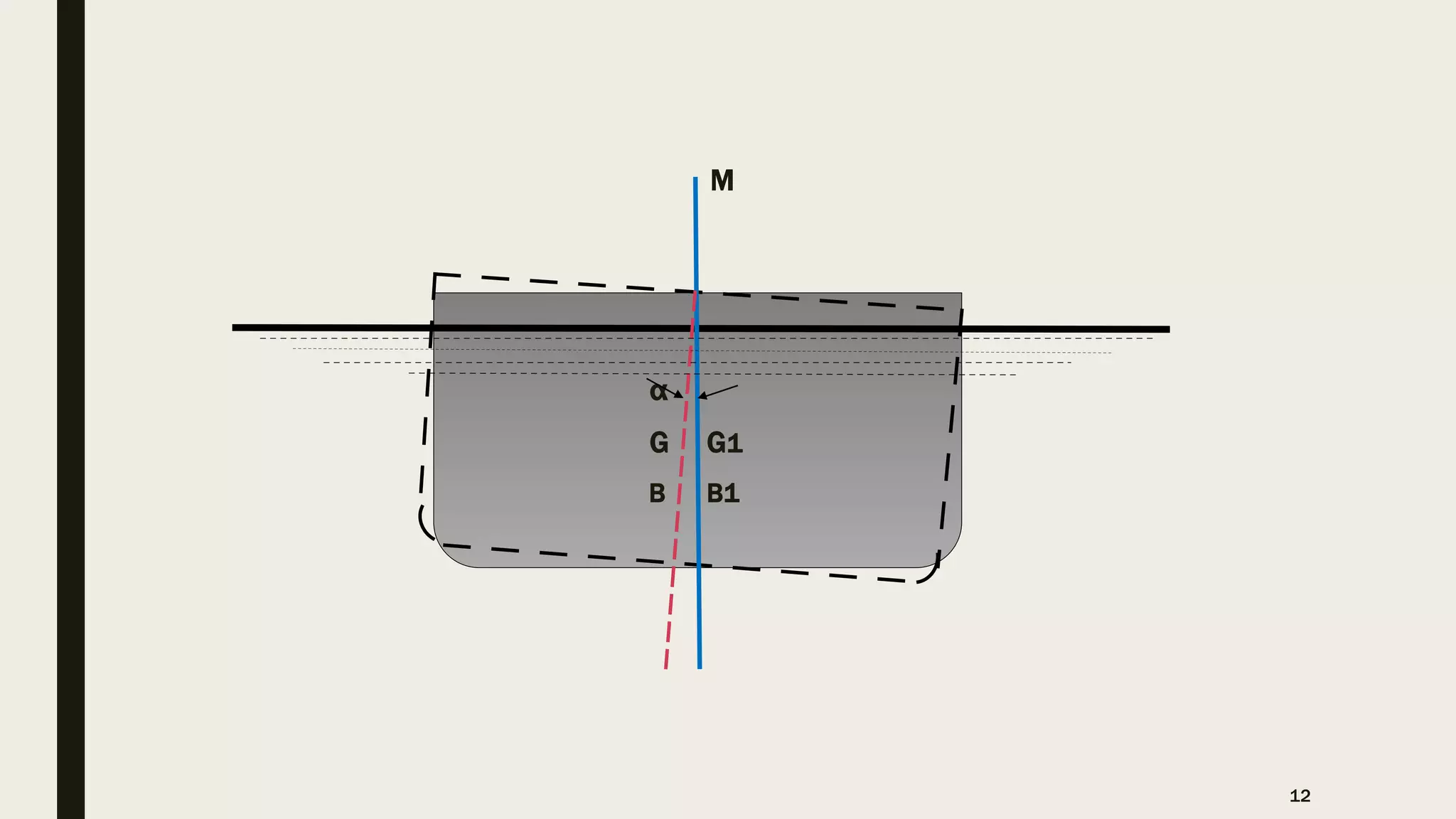
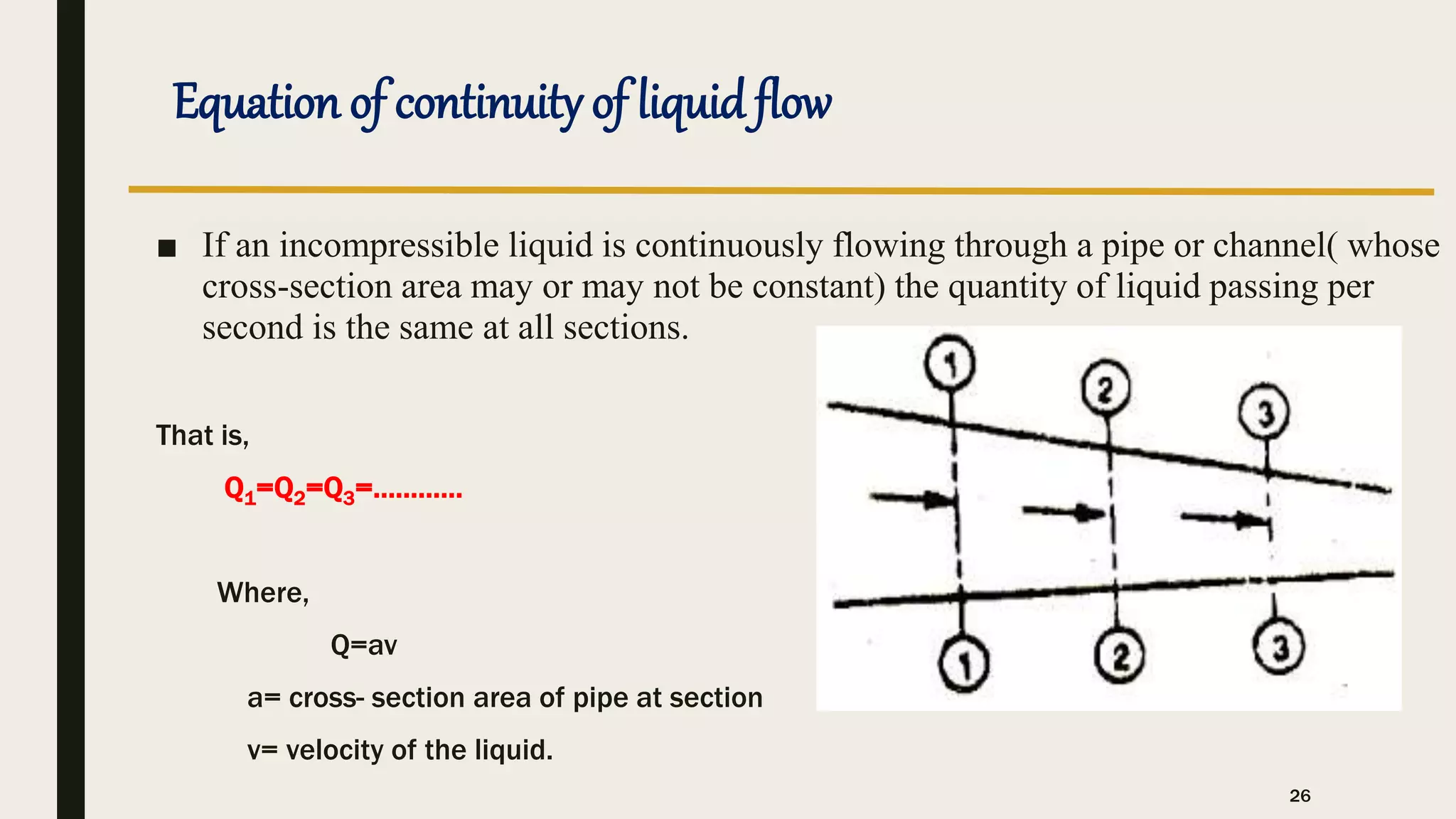
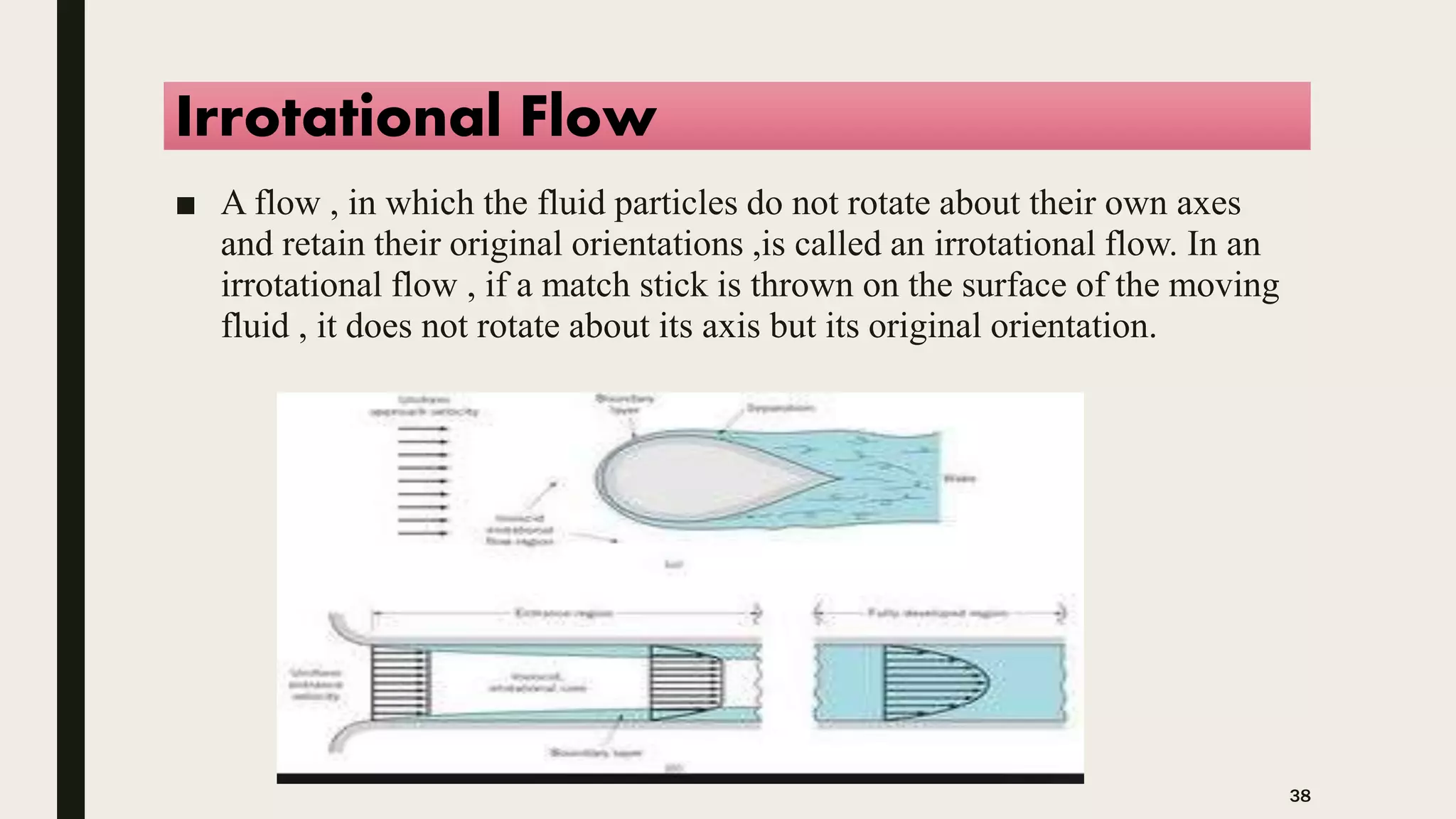
The document discusses Archimedes' principle, emphasizing buoyancy and the conditions affecting a body's ability to float or sink in a fluid. It explains key concepts such as center of buoyancy, metacenter, and metacentric height, which relate to the stability of floating bodies. Additionally, it outlines different types of fluid flows in pipes, categorizing them based on uniformity, turbulence, and compressibility.

1. 1

2. ■ Md. SumonAhmed 14207045
■ Md. Safiul Kafi 14207073
■ Md. Mahedi Hasan 14207024
■ Md. Juwel rana 14207076
■ Arman parvez 14207053
2

3. 3

4. Contents
Archimedes Principle,
Buoyancy,
Centre of Buoyancy,
Metacentre,
Metacentric Height,
Conduction of equilibrium of a floating body &
Types of Flows in a Pipe
4

5. Born:287 BC.
Died: c. 212 BC (aged around 75)
Fields: Mathematics,
Physics,
Engineering
Astronomy
Inventor
Archimedes
5

6. Archimedes' principle
 “Whenever a body is immersed wholly or partially in a fluid, it is
buoyed up (i.e. lifted up) by a force equal to the weight of the
fluid displaced by the body.”
6

7. ■ “The tendency of a fluid to uplift a submerged body,
because of the up-thrust of the fluid, is known as force of
buoyancy or simply buoyancy.”
■ The buoyant force acts vertically upward through the centroid of the
displaced volume and can be defined mathematically by Archimedes’
principle.
■ Buoyancy = weight of displaced fluid
dfd VF 
7

8.  Whenever a body is placed over a liquid, either it sinks down
or floats on the liquid.
 Two forces involve are:
1. Gravitational Force
2. Up-thrust of the liquid
 If Gravitation force is more than Upthrust, body will sink.
 If Upthrust is more than Gravitation force, body will float.
Buoyancy
8

9. 9

10. The center of buoyancy is the center of area of the immersed
section. Centre of buoyancy always act vertically upward.
10

11. ■ Whenever a body , floating in a liquid, is given a small angular displacement, is
starts oscillating about some point . This point , about which the body starts
oscillating, is called metacenter.
11

12. M
α
G G1
B B1
12

13. ■ The metacentric height (GM) is a measurement of the initial
static stability of a floating body. It is calculated as the distance
between the center of gravity of a ship and its metacenter.
■ The distance between center of gravity of a floating body and
the metacenter is called metacentric height.
 Some values of metacentric height:
– Merchant Ships = upto 1.0m
– Sailing Ships = upto 1.5m
– Battle Ships = upto 2.0m
– River Craft = upto 3.5m
13

14. 14

15.  Considering a ship floating freely in water. Let the ship be given a
clockwise rotation through a small angle q (in radians) as shown in Fig.
The immersed section has now changed from acde to acd1e1.
15

16. ■ The original center of buoyancy B has now changed to a new position B1. It
may be noted that the triangular wedge ocn has gone under water. Since the
volume of water displaced remains the same, therefore the two triangular
wedges must have equal areas.
■ A little consideration will show, that as the triangular wedge oam has come
out of water, thus decreasing the force of buoyancy on the left, therefore it
tends to rotate the vessel in an anti-clockwise direction.
■ Similarly, as the triangular wedge ocn has gone under water, thus increasing
the force of buoyancy on the right, therefore it again tends to rotate the vessel
in an anticlockwise direction.
16

17. ■ It is thus obvious, that these forces of buoyancy will form a couple, which
will tend to rotate vessel in anticlockwise direction about O. If the angle
(q), through which the body is given rotation, is extremely small, then the
ship may be assumed to rotate about M (i.e., metacentre).
■ Let l =length of ship
b=breadth of ship
q=Very small angle through
which the ship is rotated
V=Volume of water displaced by the ship
17

18. From the geometry of the figure, we find that
am=cn=bq/2
Volume of wedge of water aom
= ½ (b/2 x am)xl
= ½ (b/2 x bq/2)l (am = bq/2)
=b2ql/8
Weight of this wedge of water
=  b2ql/8 (=sp. Wt. of water)
And arm L.R. of the couple = 2/3 b
Moment of the restoring couple
= ( b2ql/8) x (2/3 b) =  b3ql/12 …(i)
18

19. --And moment of the disturbing force
=  V x BB1…(ii)
--Equating these two moments (i & ii),
 b3ql/12 =  x V x BB1
--Substituting values of:
lb3/12 = I
BB1 = BM x q in the above equation,
 . I . q   x V (BM x q)
BM = I/V
BM= Moment of inertia of the plan/ Volume of water displaced
19

20. Now metacentric height,
GM= BM  BG
+ve sign is to be used if G is lower than B and,
–ve sign is to be used if G is higher than B.
20

21. ■ A body is said to be equilibrium, when it remains in a steady
state, while floating in a liquid. There are three condition of
equilibrium of a floating body:
1. Stable equilibrium
2. Unstable equilibrium, &
3. Newtral equilibrium
21

22. Stableequilibrium
■ A body is said to be in equilibrium, if it
returns back to its original position, when
given a small angular displacement.
Metacentre above the C.G.
22

23. Unstable equilibrium
■ A body is said to be in unequilibrium, if it does not
returns back to its original position and heels further
away, when given small angular displacement. This
happens metacentre below the C.G.
23

24. Newtral equilibrium
■ A body is said to be in newtral equilibrium, if it occupies a new
position and remains at rest in the new position, when given a
small angular displacement. This happens when the metacentre
coincides with the center of gravity of the floating body.
24

25. Discharge
■ The quantity of a liquid ,flowing per second through a
section of a pipe is known as discharge or rate of
discharge.
Discharge =Area * Average velocity
Q=AV
25

26. Equation of continuity of liquid flow
■ If an incompressible liquid is continuously flowing through a pipe or channel( whose
cross-section area may or may not be constant) the quantity of liquid passing per
second is the same at all sections.
That is,
Q1=Q2=Q3=…………
Where,
Q=av
a= cross- section area of pipe at section
v= velocity of the liquid.
26

27. Motion of a Fluid Particle
27

28. Types of Flows in a Pipe
■ The type of a flow of a liquid depends upon the manner in
which the particles unite & move . Though there are many
types of flows, yet the following are important from the subject
point of view.
28

29. UniformFlow
■ A flow ,in which the
velocities of liquid
particles at all sections
of a pipe or channel are
equal, is called a
uniform flow. this term is
generally applied to flow
in channels.
29

30. Non Uniform Flow
■ A flow ,in which the velocities of liquid particles at all
sections of a pipe or channel are not equal, is called a non-
uniform flow.
30

31. Streamline Flow
■ A flow ,in which each liquid
particle has a definite path &
the paths of individual particles
do not cross each other , is
called a streamline flow . It is
also called a laminar flow.
31

32. Turbulent Flow
■ A flow ,in which each liquid particle does not have a definite
path & the paths of individual particles also cross each other ,
is called a turbulent Flow.
32

33. Steady Flow
■ A flow , in which the quality of liquid flowing per second is
constant , is called a steady flow . A steady flow may be
uniform or non- uniform.
33

34. Unsteady Flow
■A flow , in which the quality
of liquid flowing per second
is not constant, is called a
unsteady flow.
34

35. Compressible Flow
■ A flow , in which the volume of a fluid and its density
changes during the flow , is called a compressible flow .All the
gases are , generally, considered to have compressible flows.
35

36. Incompressible Flow
■ A flow , in which the volume of a flowing fluid and its density does
not change during the flow , is called a un compressible flow .All the
liquids are , generally, considered to have incompressible flows.
36

37. Rotational Flow
■ A flow , in which the fluid particles also rotate ( i.e., have some angular
velocity ) about their own axes while flowing, is called a rotational flow .
In a rotational ,if a match stick is thrown on the surface of the moving
fluid ,it will rotate about its axis…
37

38. Irrotational Flow
■ A flow , in which the fluid particles do not rotate about their own axes
and retain their original orientations ,is called an irrotational flow. In an
irrotational flow , if a match stick is thrown on the surface of the moving
fluid , it does not rotate about its axis but its original orientation.
38

39. One-dimensional Flow
■ A flow , in which the streamlines of its moving particles may be represented by straight
line, is called one-dimensional flow. It is because of the reason that a straight streamline,
being a mathematical line, possesses one dimension only i.e. either x-x 0r y-y or z-z
direction.
39

40. Two-dimensional Flow
■ A flow ,whose streamlines may be
represented by a curve , is called a
two dimensional flow .It is because
of the reason that a curved
streamline will be along any two
mutually perpendicular directions.
40

41. Three-dimensional
■ A flow ,whose streamlines may be represented in space i.e.
along three mutually perpendicular directions , is called three-
dimensional flow.
41

42. 42