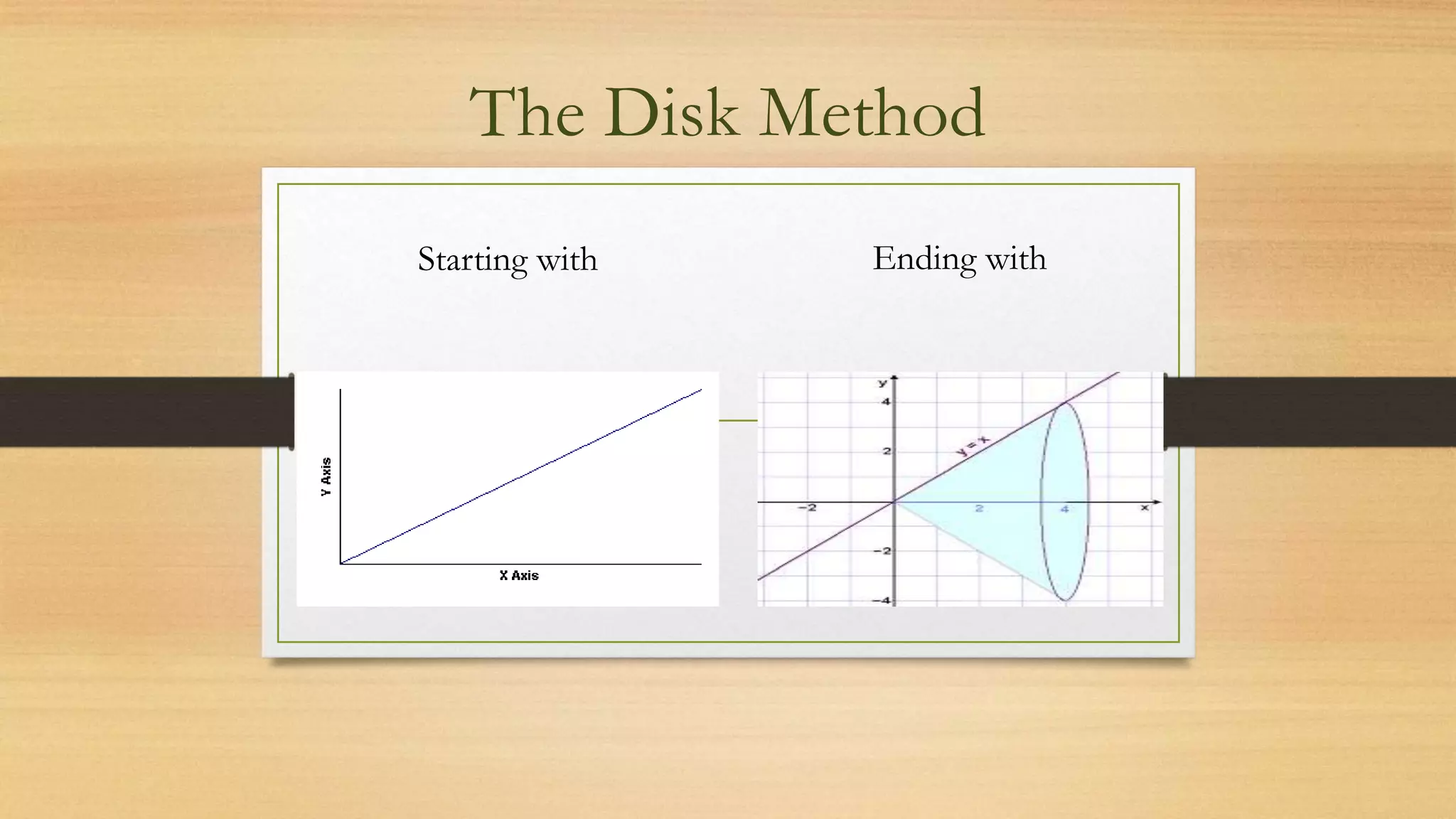
The document discusses using the disk method to calculate volumes by rotating a curve around the x-axis. It defines a disk as a solid circle, and gives the formula for the area of a disk as πr^2. A cone is a disk with height, and its volume is πr^2h/3. To find the volume of the rotating shape, we treat it as an infinite number of disks of thickness dx, and the volume of each disk is its area πr^2 times dx. Integrating this formula over the bounds of the curve gives the total volume of the rotating solid.

1. The Disk Method
Starting with Ending with

2. 𝑎
𝑏
𝑥 𝑑𝑥
Integrating y=x yield the area under the curve, but what if we wanted a volume?
First lets lay out quick some questions we will need to identify.
• What is a disk and a cone?
• What is the area of a disk?
• What is the volume of a cone?

3. The Disk!
• Simply put, a disk is a solid circle.
The area of the disk is 𝐴 = 𝜋𝑟2
π=3.14 when rounding

4. The Cone!
A cone is a disk with a height, with which the radius tapers towards a vertex.
Therefore the volume of a cone is:
𝑉 = 𝐴 𝑐𝑖𝑟𝑐𝑙𝑒 ·
ℎ
3
𝑉 = 𝜋𝑟2 ·
ℎ
3

5. Better Call Sal
Now that we have our area and volume, lets have Sal from Khan Academy
give us a quick sketch on rotating our graph.
Note that Sal is using the equation 𝑦 = 𝑥2, we will be using 𝑦 = 𝑥,
Just click the video and adjust the time to 1:49

6. Creating our Disk Equation
Solving for Area of a disk leaves us with only 2 variables:
π and r
But pi is already 3.14… so we only need to find r
Since the radius is the distance from the center to the edge, and the center is our x-axis, then the edge must be the
height of the graph. This would be our equation valued at that point.
Therefore: 𝑟 = 𝑦 = 𝑓(𝑥)
That leaves us with: 𝐴 = 𝜋𝑟2
= 𝜋(𝑓 𝑥 )2

7. How Many Disks are in a Cone?
So how do we go from a 2-D disk to a 3-D cone?
What if we kept adding disks to disks to shape our cone,
each new disk having a decreasing radius?
Recall back to Reimann Sums. How can we define each
iteration of disks infinitesimally smaller than the previous?
Hint on slide 2

8. The Integrand, dx, and You.
We have our disk of infinitesimally small height. Giving us a volume equation per disk of:
𝑉 = 𝐴 · h
𝑉 = (π 𝑓 𝑥
2
· 𝑑𝑥
We want to then find the volume of the whole cone much like we have done to find the area
under the curve.
Introducing Integration(again)!
𝑉

9. Completing Our Cone
We started with the line
𝑦 = 𝑥
But with our new equation
𝑉 = 𝐴 · ℎ = 𝜋𝑟2
· 𝑑𝑥 = (π(𝑥)2
) · 𝑑𝑥
We have our cone!

10. Summary and…
V= ʃA*h
A= π*r^2
r= f(x)
h= dx
Formula Cheat Sheet
Now that we know the Disk Method for integrating, how
would the shape of our volume change if we instead:
• Rotated about the y-axis?
• Rotated about the z-axis?
• Rotated about another line/curve?
How would we get volume like this?