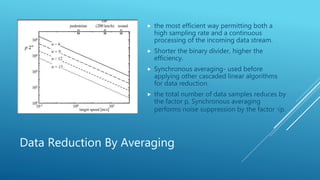
The document discusses ultra-wideband (UWB) sensor electronics focusing on m-sequence correlators used for measuring impulse response functions (IRF) of test objects. It explores the generation and advantages of binary pseudo-noise codes, particularly m-sequences, and the technical challenges in interpreting UWB signals. The text highlights the necessity of correlators for impulse compression and signal detection amidst noise, along with the methods for data processing and optimization in UWB systems.

1. Focus on M-sequence sensor electronics
IR-UWB: Correlator
-Jayendra Mishra

2. UWB Principle Of Operation
 Ultra-wideband sensors stimulate their
test objects with pulses.
 UWB pulses allows following the
propagation and the temporal
development of energy distribution
within the test scenario
 Multiple chirp signals of sub
nanoseconds spread over a large
bandwidth are generated to get an
impulse response.

3. Measurement Complexity
 Large peak power signals represents some inconvenience of the
impulse measurement technique.
 Idea is to go away from excitations by strong single or infrequent
‘shocks’ and to pass instead to a stimulation of the DUT by many subtle
‘pinpricks’.
 Binary pseudo-noise codes represent pulse signals which are more
careful with the test objects.

4. Binary
Pseudo-Noise
Codes
 Pulse signals which have spread their energy homogenously over the whole signal length. Hence, their
peak voltage remains quite small by keeping sufficient stimulation power.
 PN-codes are periodic signals which constitute of a large number of individual pulses ostensible
randomly distributed within the period. The theory of PN-code generation is closely connected with
Galois-fields and primitive polynomials.
 Summarized by the term binary PN-code they may have three (-1, 0, 1) and more signal levels.
 Amalgamated properties of two signal classes
 Periodic-deterministic signals
 Random signals
 Pseudo-noise codes examples: Barker code, M-sequence, Golay-Sequence, Gold-code, Kasami-code

5. M-Sequence
 Maximum length binary sequence or shortly
termed M-sequence is Simple to generate
and provide best properties to measure the
Impulse response function IRF.
 For a given signal power, lowest amplitude
and shortest autocorrelation function.
 No. of flip-flops in shift register determine
the length of M-sequence
 Spares the measurement objects and the
requirements onto the receiver dynamic
are more relaxed.

6. M-sequence Generation
 Digital shift registers with appropriate
feedbacks.
 Shift the starting point of the M-
sequence to control the time lag of an
UWB correlator.
 In figure the register is of the 9th order.
 Fibonacci structure deals with cascaded
XOR-gates which increase the dead time
before a new change of the flip-flop
states is allowed.

7. Technical
Challenges
 IRF measurement not directly possible with a time extended
signal such as the M-sequence.
 The M-sequence signal has to be subjected to an impulse
compression to gain the wanted impulse response.
 The price to pay for reduced voltage in a UWB signal is the
chaotic structure of the receive signal, therefore, a correlator
is required for interpretation.
 Intermediate frequency cannot provide a low freq. as the
Nyquist bandwidth is huge for 3 GHz of bandwidth.
 To perform the correlation of a very wideband signal we
need.
 Cross-correlation to access the wanted IRF
 Digital impulse compression
 Frequency domain conversion

8. Impulse
Correlator
 Objective: to determine the impulse response function of a
test object.
 A correlator is used to detect the presence of signals with a
known waveform in a noisy background.
 The output is nearly zero (below set threshold) if only noise
is present.
 Impulse compression is performed by the correlator

9. Impulse
Correlation
 In UWB, Impulse compression using wideband correlation
 Convolving with a time inverted stimulus x(-t).
 Technical implementation Cross-correlation
 The Sliding correlator
 PN- correlation

10. The Sliding
Correlator
 (a.1) Two shift registers of identical behavior make a
sliding correlator. First one provides actual band
limited stimulus signal at fc, and second serves as
reference to perform correlation fs = fc-Δf.
 (a.2) Both shift registers have to run in parallel with
constant time lag during this time.
 (b.1) Integrator of the product detector is crucial for
the noise suppression and it largely determines the
overall sensitivity of the sensor device.
 (b.2) Waveform sweeping over the initial states of
each of the shift registers to get sampled version of
correlation function. Rather sliding, the correlator
jumps in steps of Δtc = 𝑓𝑐−1
.
 This gives sampled version of correlation function.
 Sampling interval equals the M-sequence chip
duration.

11. Block Diagram Of UWB Correlator
 Digital ultra-wideband correlation joins
sliding correlator and stroboscopic
sampling.
 Sub-sampling: data gathering is
distributed over several periods by
capturing the signal with the lower
sampling rate fs.
 Since No. of chips: Ns = N = 2 𝑛
− 1 ,n is
the order. sub sampling is simply
controlled by a binary divider.
 The placement of the anti-aliasing filter
depends on the measurement
environment.

12. Sub-Sampling Control By Binary Divider.
 Goal is in to organize a precise and simple sub-
sampling control.
 Interleaved sampling approach for single stage
binary divider; so, two stage divider would have
four periods of measurements.
 In figure, 3rd order M-sequence with 7 chips or
data samples.
 For every beat of the clock generator the voltage
is captured at every second beat.
 So, first the odd chip numbers are captured and
then the even ones.
Wanted results: IRF or FRF of DUT.

13. Data Reduction By Averaging
 the most efficient way permitting both a
high sampling rate and a continuous
processing of the incoming data stream.
 Shorter the binary divider, higher the
efficiency.
 Synchronous averaging- used before
applying other cascaded linear algorithms
for data reduction.
 the total number of data samples reduces by
the factor p, Synchronous averaging
performs noise suppression by the factor √p.

14. Digital Impulse
Compression
 If only round trip time is of interest we can apply
correlation between receive signal y(t) and the ideal
m-sequence m(t), for faster implementation. Where
IRF shape is less important.
 The known M sequence data samples arranged in the
circulant matrix Mcirc are rearranged in Hadamard
matrix for faster computing in Fast Hadamard
transform (FHT). Figure shows the Hadamard butterfly.
 ENOB-number of receiver that includes the
quantization noise and the thermal noise.
 FHT-butterfly is used which only includes sum or
difference operations which can be executed at high
processing speed.
 the correlation leads to a noise suppression by the
factor √Ns = √(2 𝑛
-1). The equation shown in figure is
equivalent to the signal with Max. SNR obtained afte
FFT or FHT operation.

15. Design Tetrahedron Of Digital Ultra-Wideband
Correlator
Binary divider length- relaxes the speed requirements onto
the receiver. Large dividing factor reduces data throughput
but also largely reduces sensitivity of receiver.
Recording time Tr- number p of averaging controls
recording time length. Target speed and acceleration, and
the rate of mechanical object oscillations are the dominant
parameters restricting the recording time in radar
measurements.
Pre-processing- An M-sequence sensor is typically
equipped with FPGA for data processing as
• Data reduction by averaging or Background removal
• Digital impulse compression or correlation
• Data conversion into frequency domain and error
correction, detection; round trip time estimation.

16. KNOCK YOUR SELF OUT!