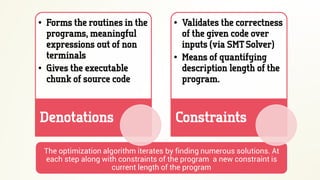
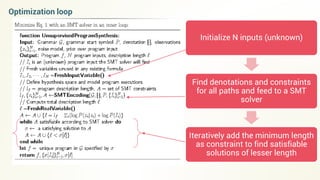
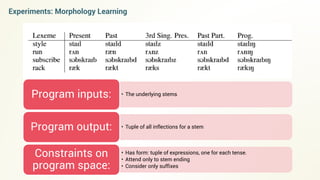
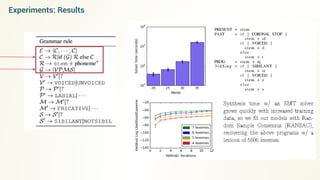
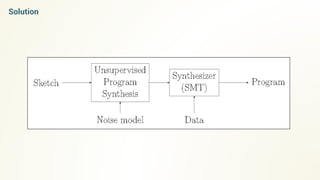
- The document discusses program synthesis through solving optimization problems to find the shortest program that fits the given observations and constraints. - It proposes using probabilistic context-free grammars to define the search space of possible programs and casting the problem as finding a satisfying assignment for a set of constraints over the program variables. - An iterative algorithm is described that finds program solutions, adds a minimum length constraint, and repeats to find shorter programs that still satisfy the constraints.

2. Motivation – 1
Drawing Visual Concepts
Dataset - Human Drawn Shape
Synthesize
Program
.
.
Goto(r1,0);
draw(shape1);
Goto(r3,10);
draw(shape3);
assert (contains 1 0);
.
.
Execute
Goto(r1,0)
Routine
(given as primitives)
argument
Machine OutputProgram(I1)
Ii – Input representation
for the input.
1
2 3

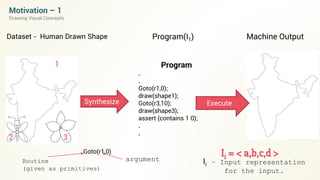
3. Motivation – 2
Learning Morphological Rules
Style, styled
hatch,hatched
Articulate,articulated
Pay,paid
Lay,laid
Need,needed
Program
if [ property1.value1 == True ]
(stem + d)
elseif [ property3.value2 > 5 ]
(stem +ed)
Elseif [property4.value5 == “y”]
(stem + id)
Synthesize Execute
Style, styled
hatch,hatched
Articulate,articulated
Pay,paid
Lay,laid
Need,needed
Run,ran
Noise
<stem, word in past tense>
Program(snatch) = snatched

4. Can we quantify the length of the Program description?
Can we quantify the length of dataset encoded/represented
in terms of the properties as required by the program ?

5. • Can we cast the problem as an optimization
problem, so that we can find an optimal
solution i.e. program & data encoding with
the minimum description length
Optimization
Problem
• Task is about compressing the data, and yet
represent the same in terms of interpretable
entities i.e. Logical Dimensionality reduction
Logical
Dimensionality
Reduction
Introduction

6. Problem Framing
Description length priors over programs Pf (·), (eg, linguistic rules)
Priors over the inputs I, PI (·) to f,(eg, stems)
N observations, { xi }i = 1 to N , (eg, words)
Noise model: Px|z(· | ·) , where z I is defined as f(Ii)

7. Plate Diagram

8. Solution
• Manually provide a rough
outline of the program to
be induced.
• Also called as sketch
• probabilistic context-free
grammar
• automatically translate
sketches into Satisfiability
Modulo Theories (SMT)
problems.
• Intractable in general, but
often solved efficiently in
practice (Formal
verification)

9. Solution

10. A context-free grammar (CFG) is a 4-tuple G = (N,Σ, R, S) where:
• N – Non terminals set | Σ – Terminals set | R - is a finite set of rules of the form
X→Y1Y2. . . Yn , where X ∈ N, n ≥ 0 , and YI ∈ ( N ∪ Σ) for I = 1. . . N
CFG

11. A context-free grammar (CFG) is a 4-tuple G = (N,Σ, R, S) where:
• N – Non terminals set | Σ – Terminals set | R - is a finite set of rules of the form
X→Y1Y2. . . Yn , where X ∈ N, n ≥ 0 , and YI ∈ ( N ∪ Σ) for I = 1. . . N
A PCFG is a CFG with a probability on production rules i.e. G = (N,Σ, R, S, q)
• q - Probabilities on the production
PCFG

12. PCFG - Sketch
Define the
program
primitives.
Constrain
the program
space with a
PCFG

13. Sketch AND/OR Graph
OR Node corresponnds to choice
AND node corresponds to descendant
Each program is a path through the AND/OR
Graph
Recursiveness helps to have paths of any
length.
Currently authors bound the length (arbitrary
constant)
Ci
j – is a Boolean value 1 or 0, depending on
which production is being derived
All the edges in a path will have value 1. All
others will be 0
OR
AND
OR

14. Constraints The SMT Solver can verify the
correctness of the path over inputs
when the path is represented as a set
of constraints.

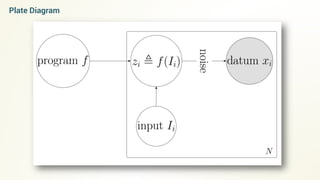
15. Denotations
Mathematical Objects, that describe
the meaning of entities in a
language
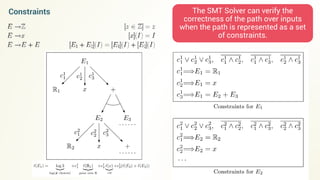
Every node in the selected path has
a denotation
In denotation, each non-terminal is
an expression (or a routine), which
takes an input I and the range for
the output is known
The path will give the sequence of
the routines with the appropriate
values for the arguments, which is
obtained from the input
[Expression] (Input) = Output
The output is dependent on the input

16. The optimization algorithm iterates by finding numerous solutions. At
each step along with constraints of the program a new constraint is
current length of the program

17. Initialize N inputs (unknown)
Find denotations and constraints
for all paths and feed to a SMT
solver
Iteratively add the minimum length
as constraint to find satisfiable
solutions of lesser length
Optimization loop

18. Tress rooted at
each non-terminal
Descendants in the
trees rooted at non
terminal
Encoding of the Input w.r.t.
the program
Encoding the programs for SMT
Calculate length
of the program
Denotation of the
program
Form the
constraints

19. •shapes, coordinates, distances, angles,
scales
Program
inputs:
•Image parse
Program
output:
•control a turtle, but:
•Restricted to alternatingly moving and
drawing
•No arithmetic on real variables
•No rotation of shapes
Constraints
on program
space:
Experiments: Visual Concepts

20. • Comparing human performance on
the SVRT with classification accuracy
for machine learning approaches.
• Human accuracy is the fraction of
humans that learned the concept: 0%
is chance level.
• Machine accuracy is the fraction of
correctly classified held out examples:
50% is chance level.
• Area of circles is proportional to the
number of observations at that point.
• Dashed line is average accuracy.
• Program synthesis: this work trained on 6
examples. ConvNet: A variant of LeNet5
trained on 2000 examples. Parse (Image)
features: discriminative learners on
features of parse (pixels) trained on 6
(10000) examples. Humans given an
average of 6.27 examples and solve an
average of 19.85 problems
Experiments: Results

21. Experiments: Morphology Learning
• The underlying stemsProgram inputs:
• Tuple of all inflections for a stemProgram output:
• Has form: tuple of expressions, one for each tense.
• Attend only to stem ending
• Consider only suffixes
Constraints on
program space:

22. Experiments: Results

23. Thanks