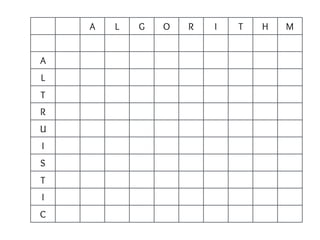
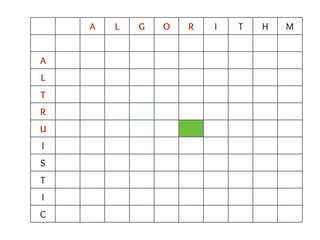
This document discusses dynamic programming techniques for three problems: edit distance, longest increasing subsequence, and matrix chain multiplication. It provides examples of how to calculate the edit distance between two strings by finding the minimum cost of insertions, deletions, and replacements needed to convert one string to the other. It then explains how to find the longest increasing subsequence of a given array using dynamic programming by building up the solution bottom-up. Finally, it briefly mentions finding the most efficient way to multiply a chain of matrices using dynamic programming.

1. CS 321. Algorithm Analysis & Design
Lecture 14
Dynamic Programming
Edit Distance Revisited
Longest Increasing Subsequence
Matrix Chain Multiplication

2. A L G O R I T H M
A
L
T
R
U
I
S
T
I
C

3. A L G O R I T H M
A
L
T
R
U
I
S
T
I
C

4. A L G O R
A L T R U

5. A L T R U
A L G O R

6. A L T R U
RA L T R U
Cost of converting ALGO to ALTRU
+
Cost of deleting R from the end

7. A L G O R
A L T R U

8. A L G O R
A L T R U

9. A L T R U
A L T R
Cost of converting ALGOR to ALTR
+
Cost of inserting U at the end

10. A L G O R
A L T R U

11. A L T R
A L G O R
U

12. RA L T R
Cost of converting ALGO to ALTR
+
Cost of replacing R with U
A L T R U
U

13. To find the edit distance between
ALGOR and ALTRU…
or convert ALGO to ALTRU and delete R
or convert ALGO to ALTR and replace R with U
Either convert ALGOR to ALTR and insert U

15. Longest Increasing Subsequence
1, 2, 3, 9, 4, 5, 10, 6, 7, 12, 13, 14, 8, 6, 17
1, 2, 3, 9, 4, 5, 10, 6, 7, 12, 13, 14, 8, 6, 17
1, 2, 3, 9, 4, 5, 10, 6, 7, 12, 13, 14, 8, 6, 17

16. LIS[i] = longest increasing subsequence
of the array L[1…i].
(What we want)
(Build up the array bottom to top.)
A = [a1, a2, … , ai, … , an]
LIS[i] = max(LIS[i-1] + 1, LIS[i-1])

17. LIS[i,j] = LIS of A[1…i]
where all elements are at most A[j].
(What we want)
(Build up the array bottom to top.)
A = [a1, a2, … , ai, … , an]
LIS[i,j] = LIS[i-1,j] or max(LIS[i-1,i] + 1, LIS[i-1,j])