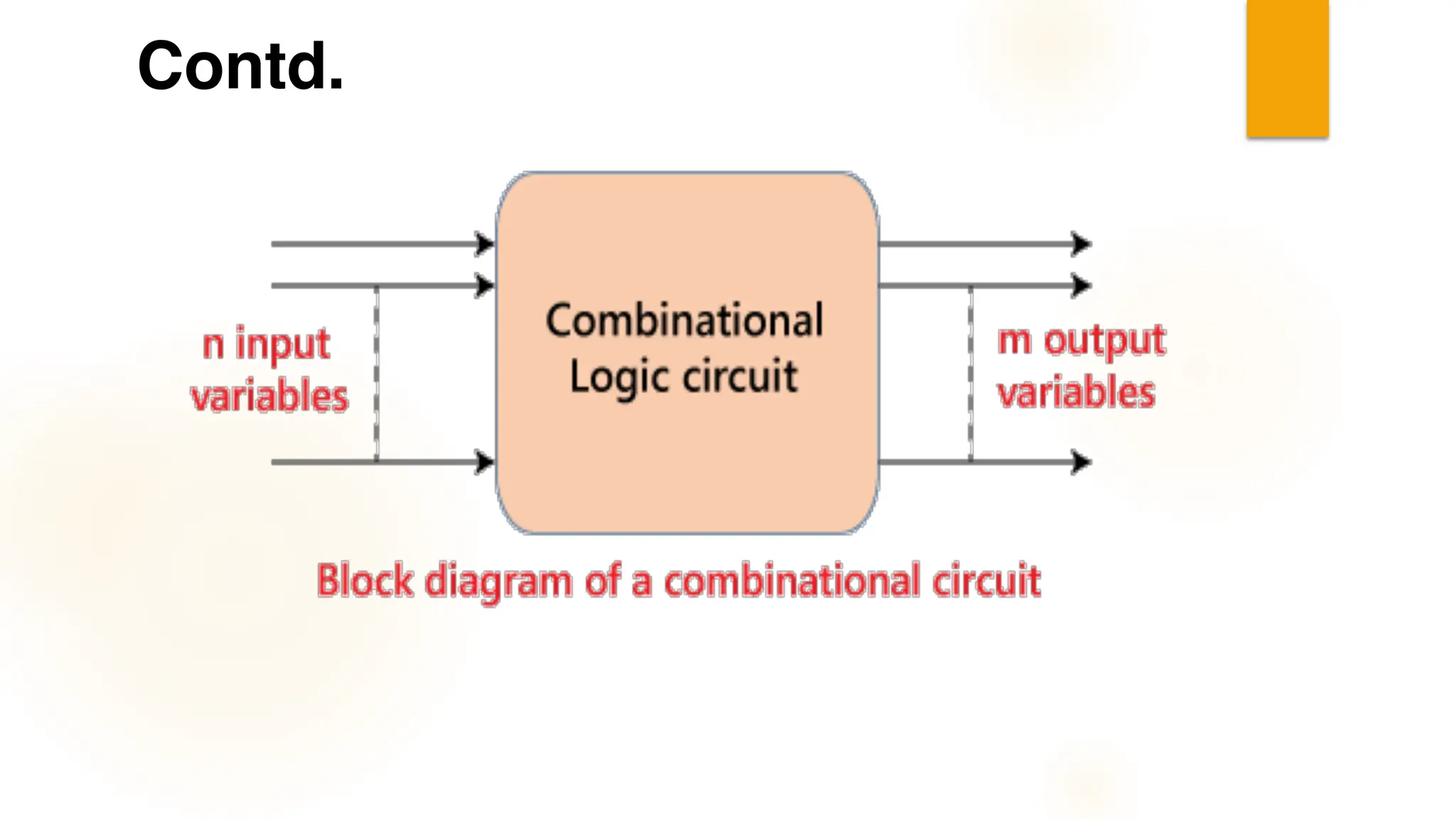
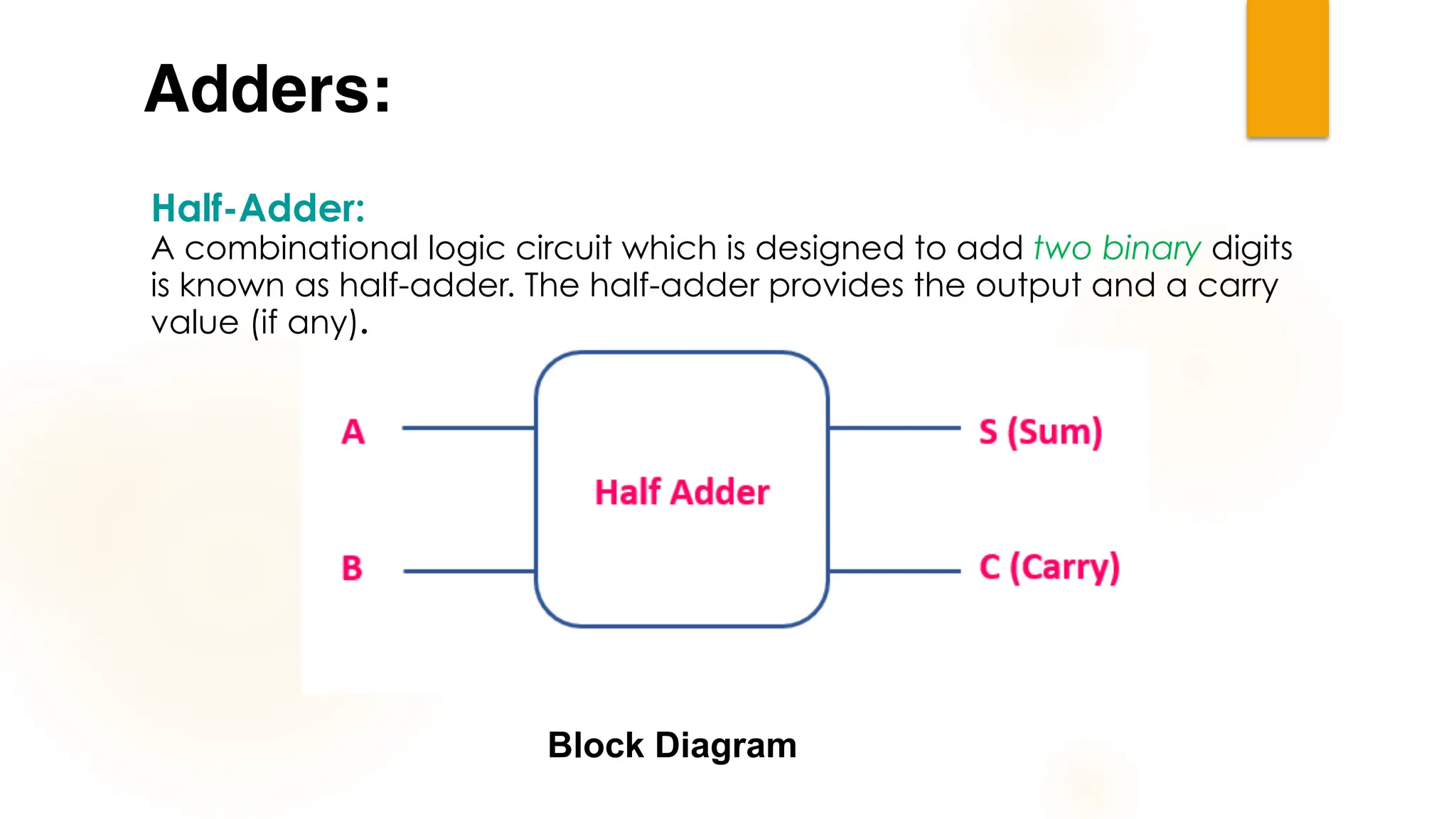
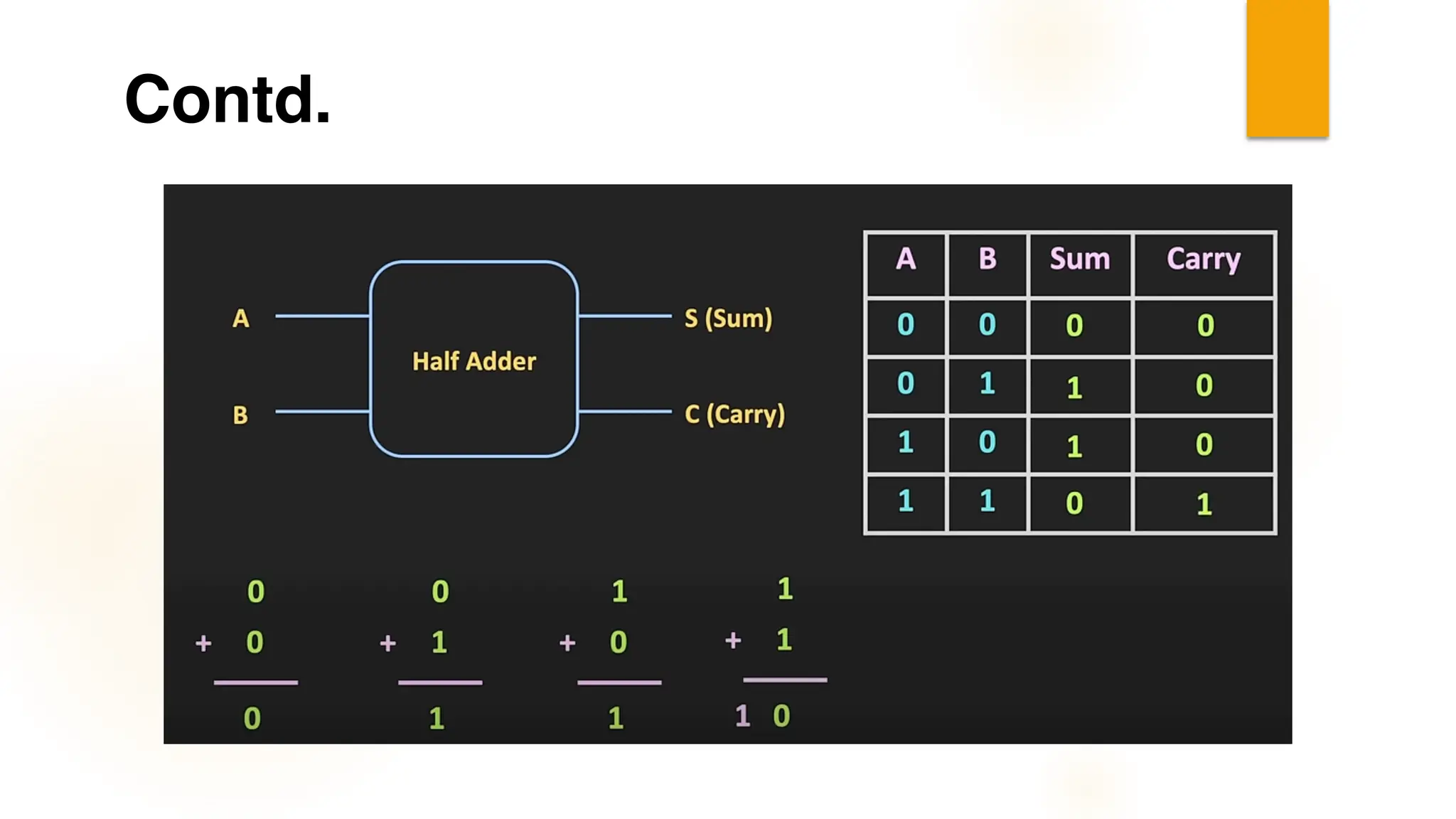
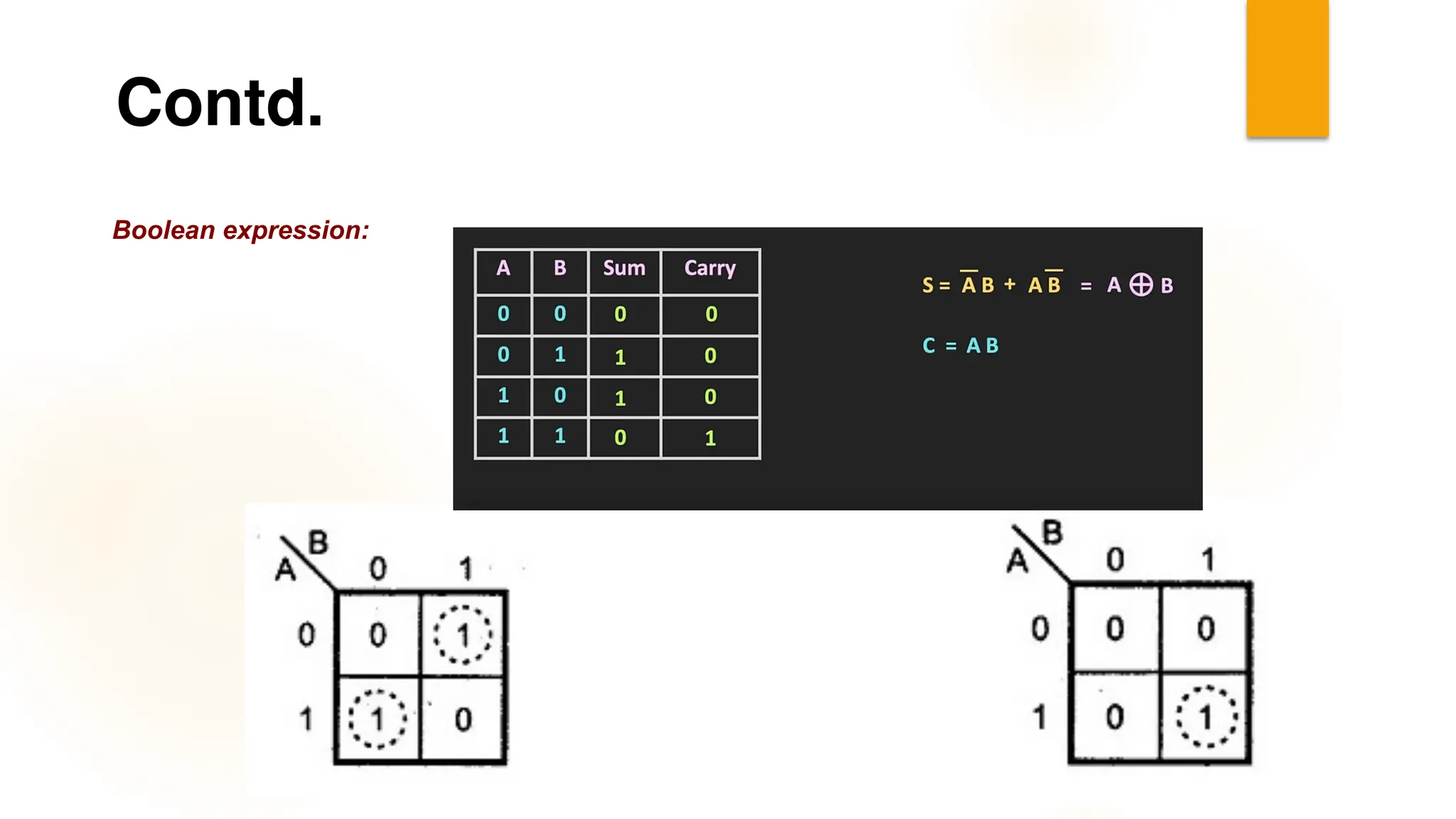
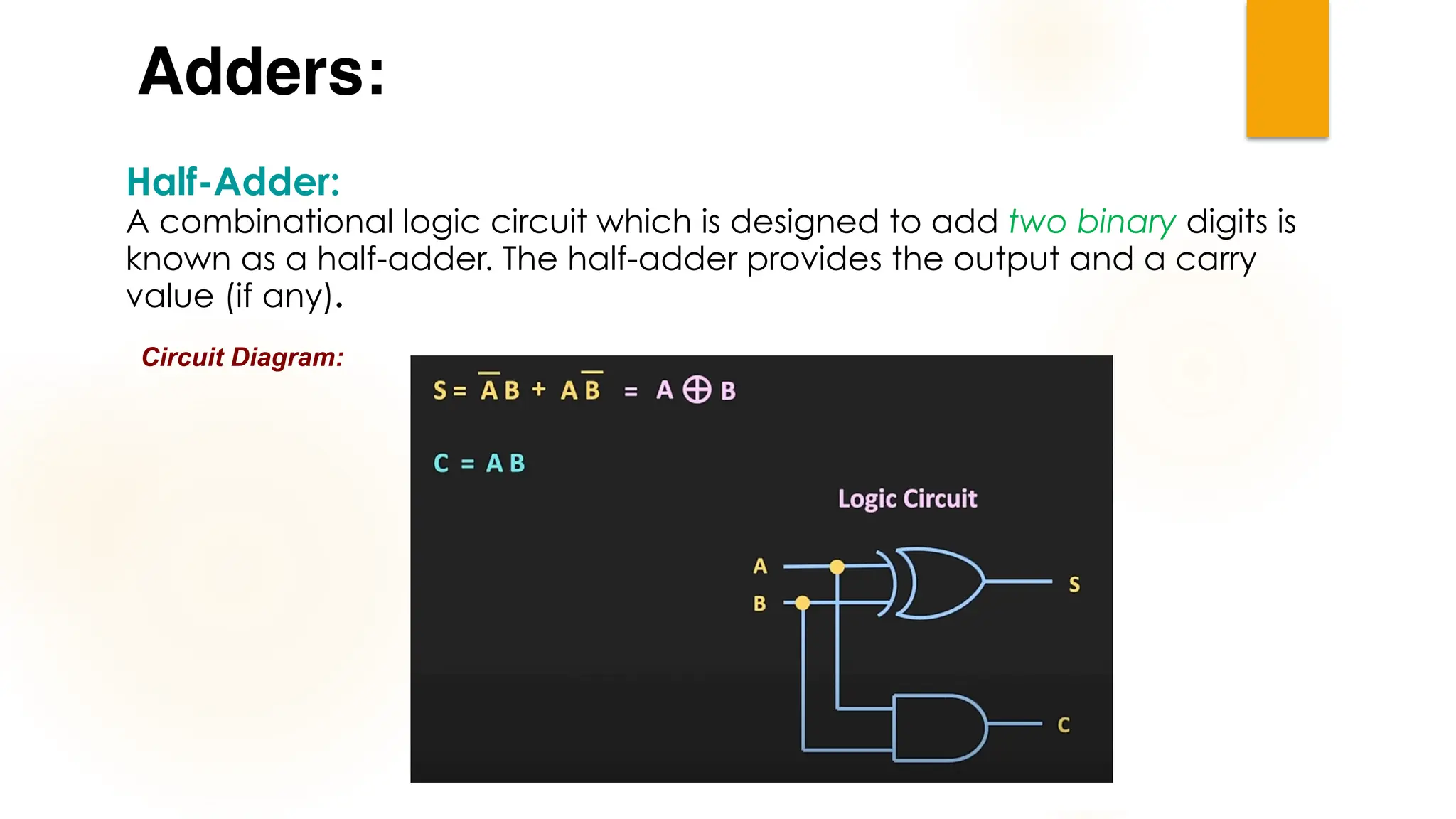
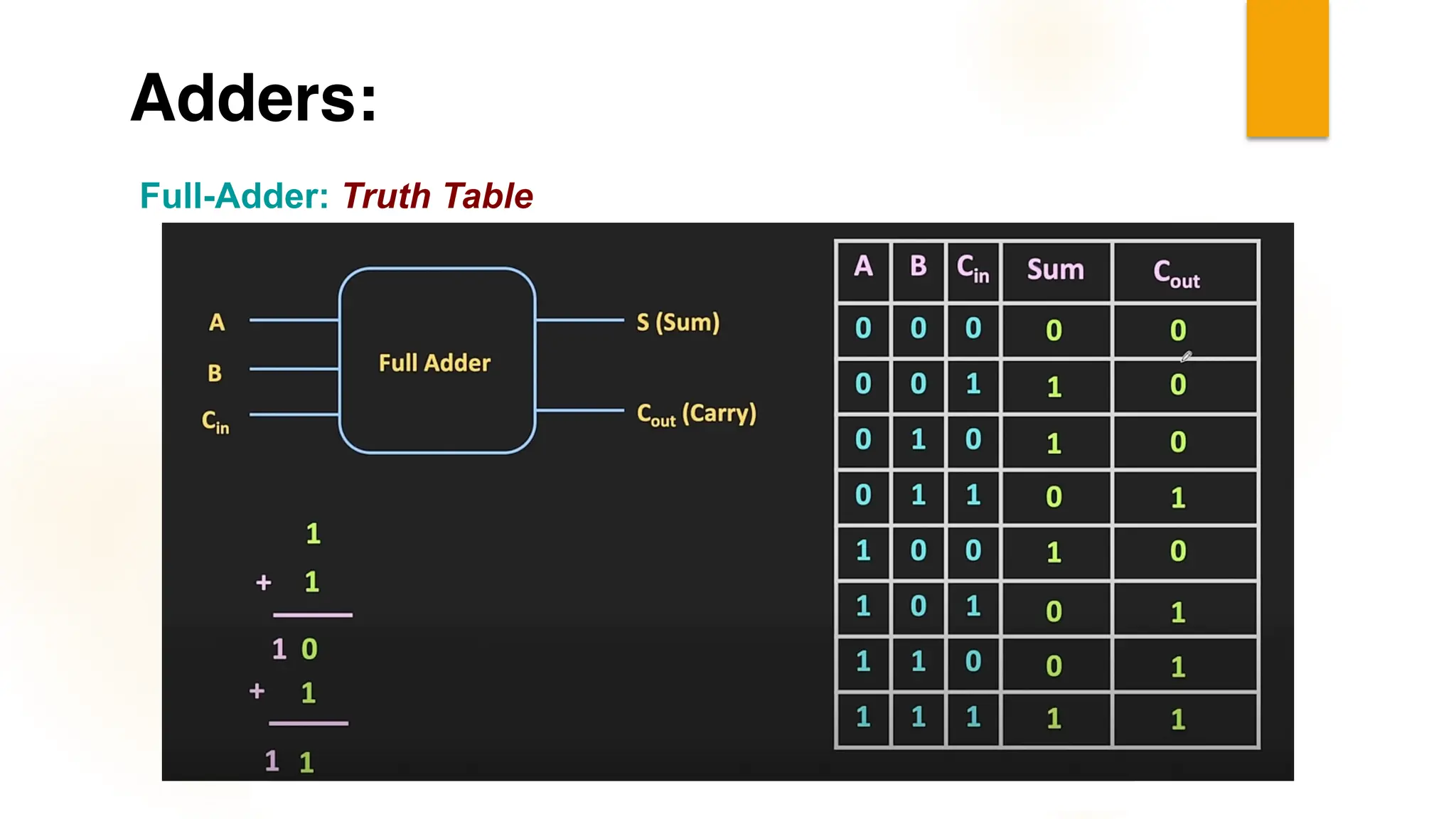
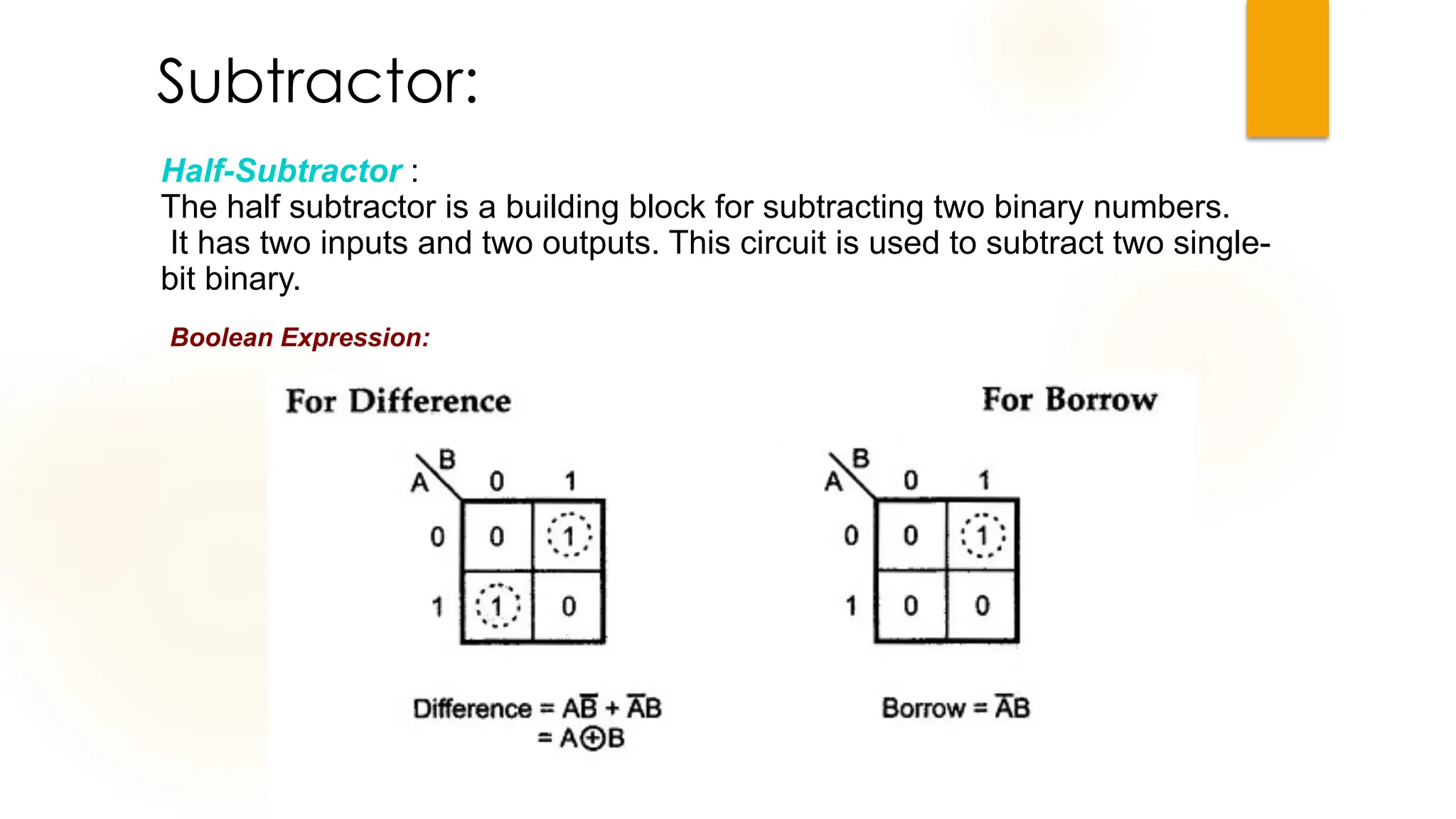
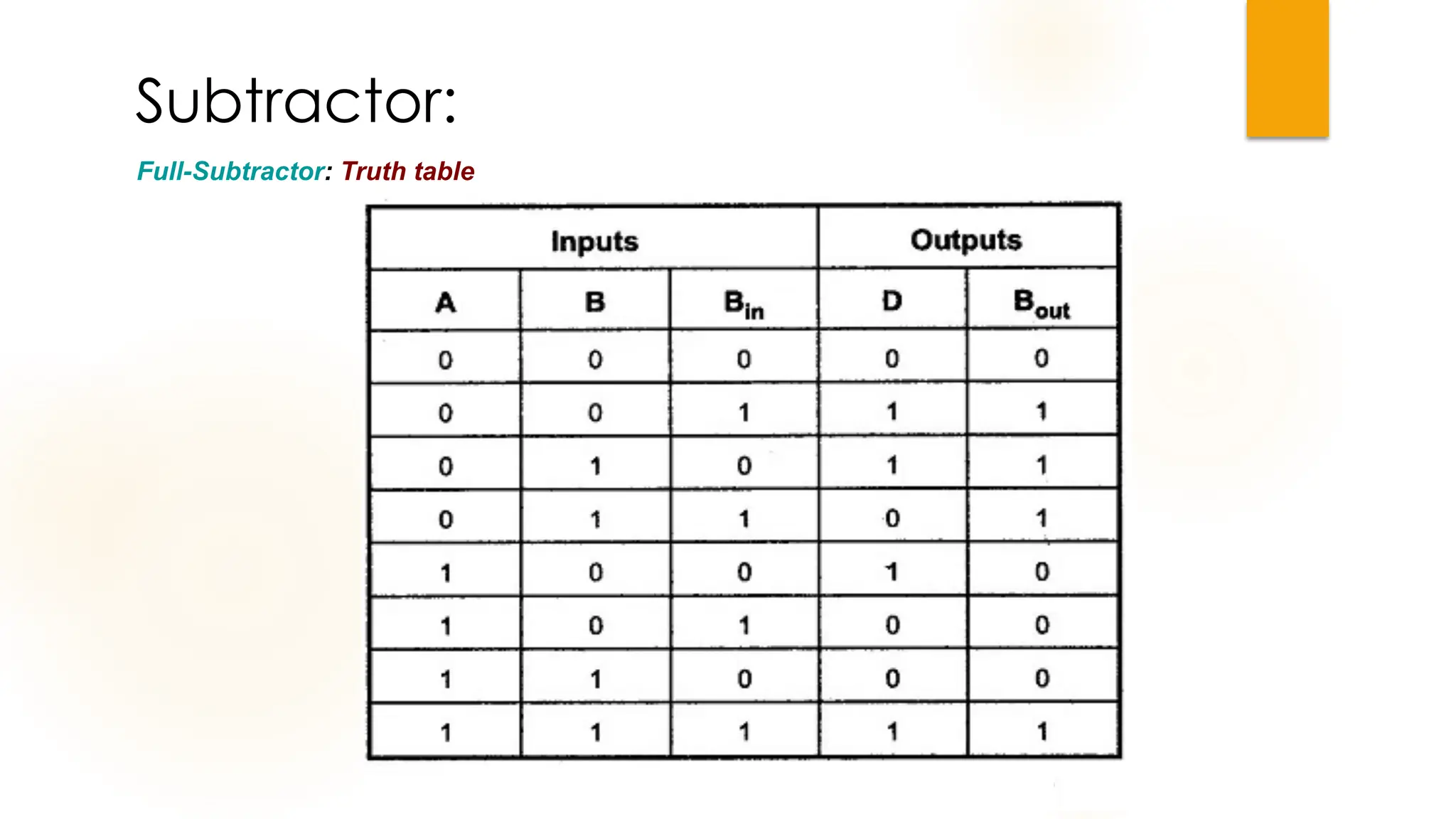
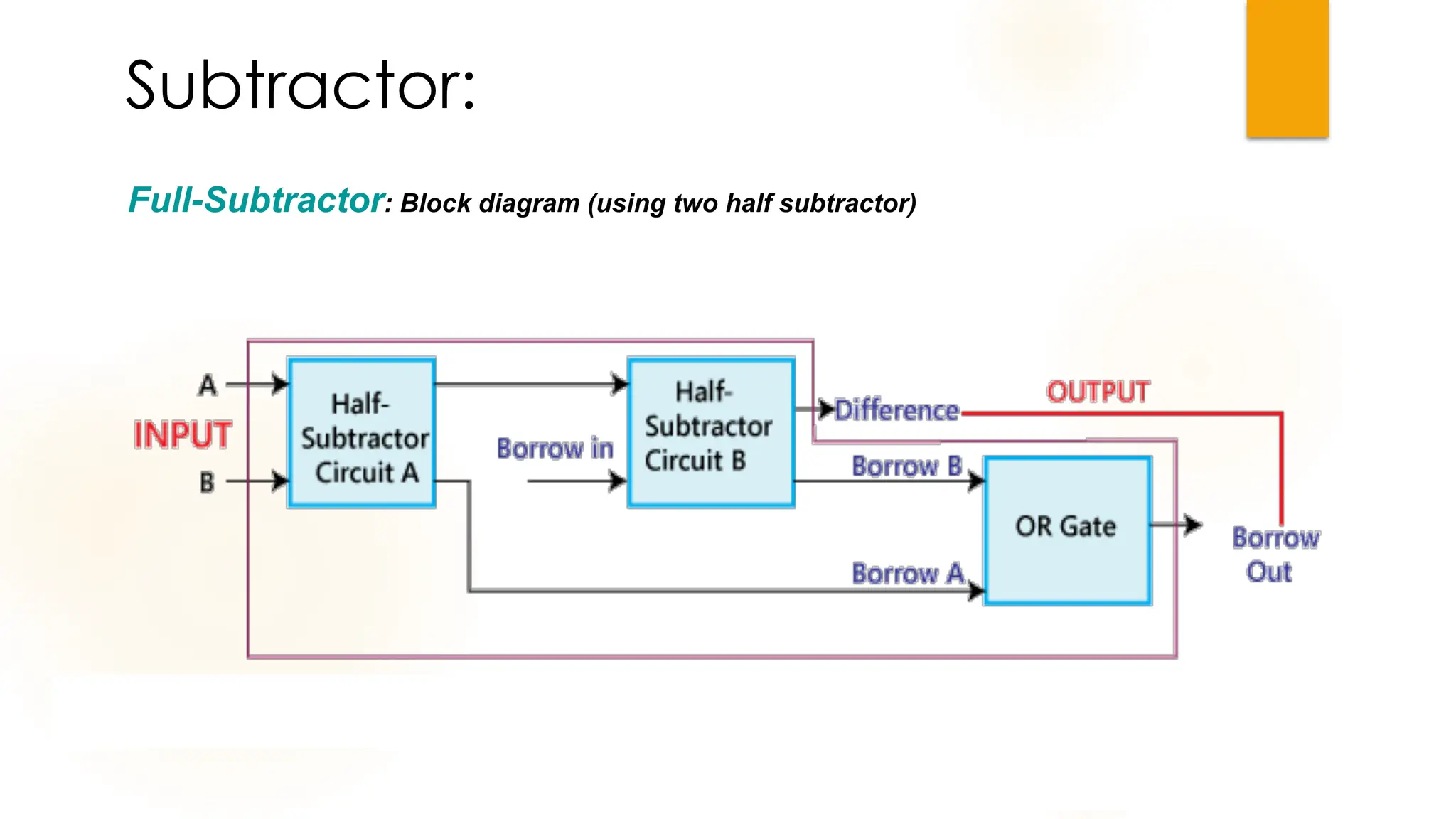
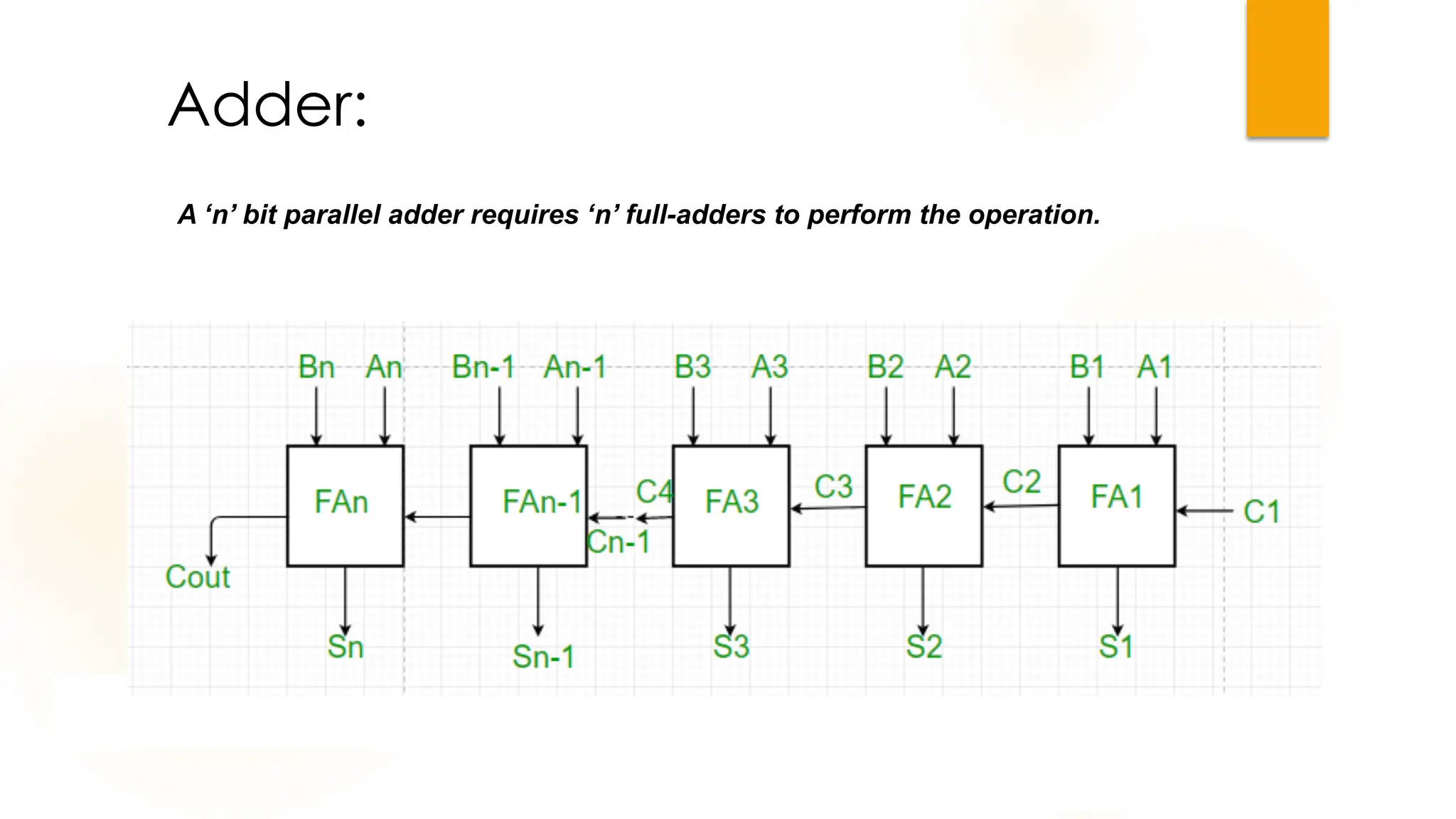
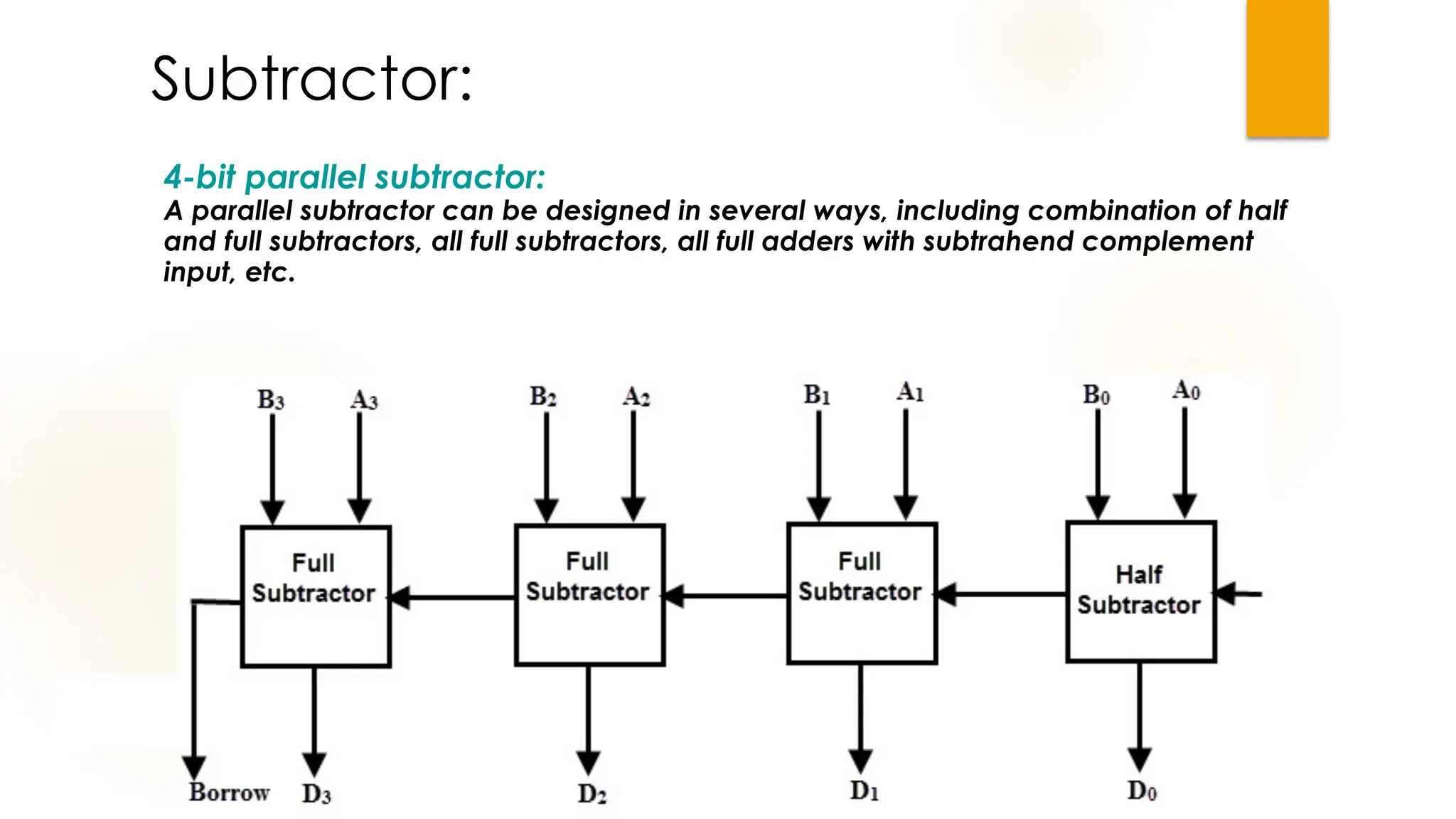
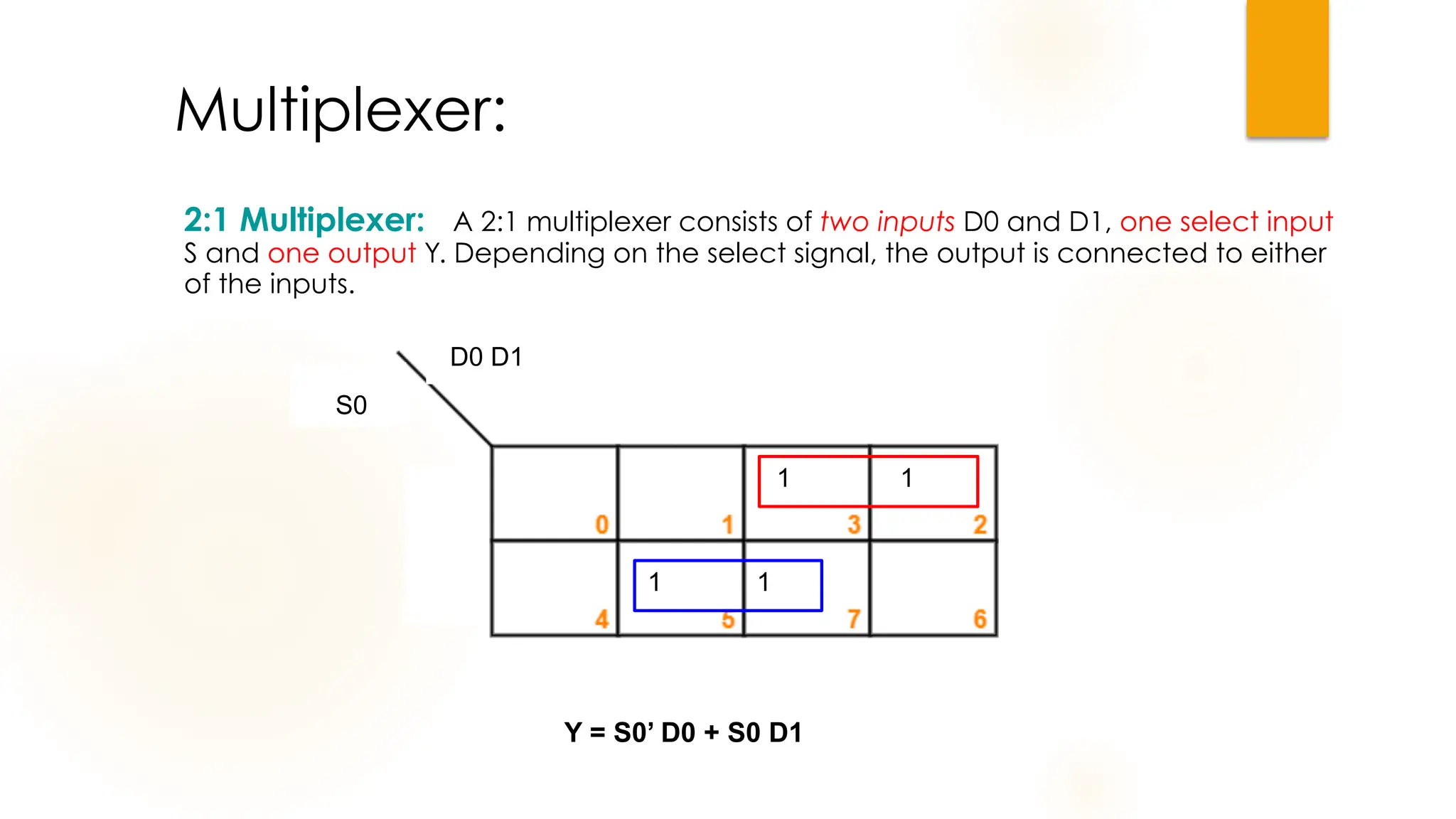
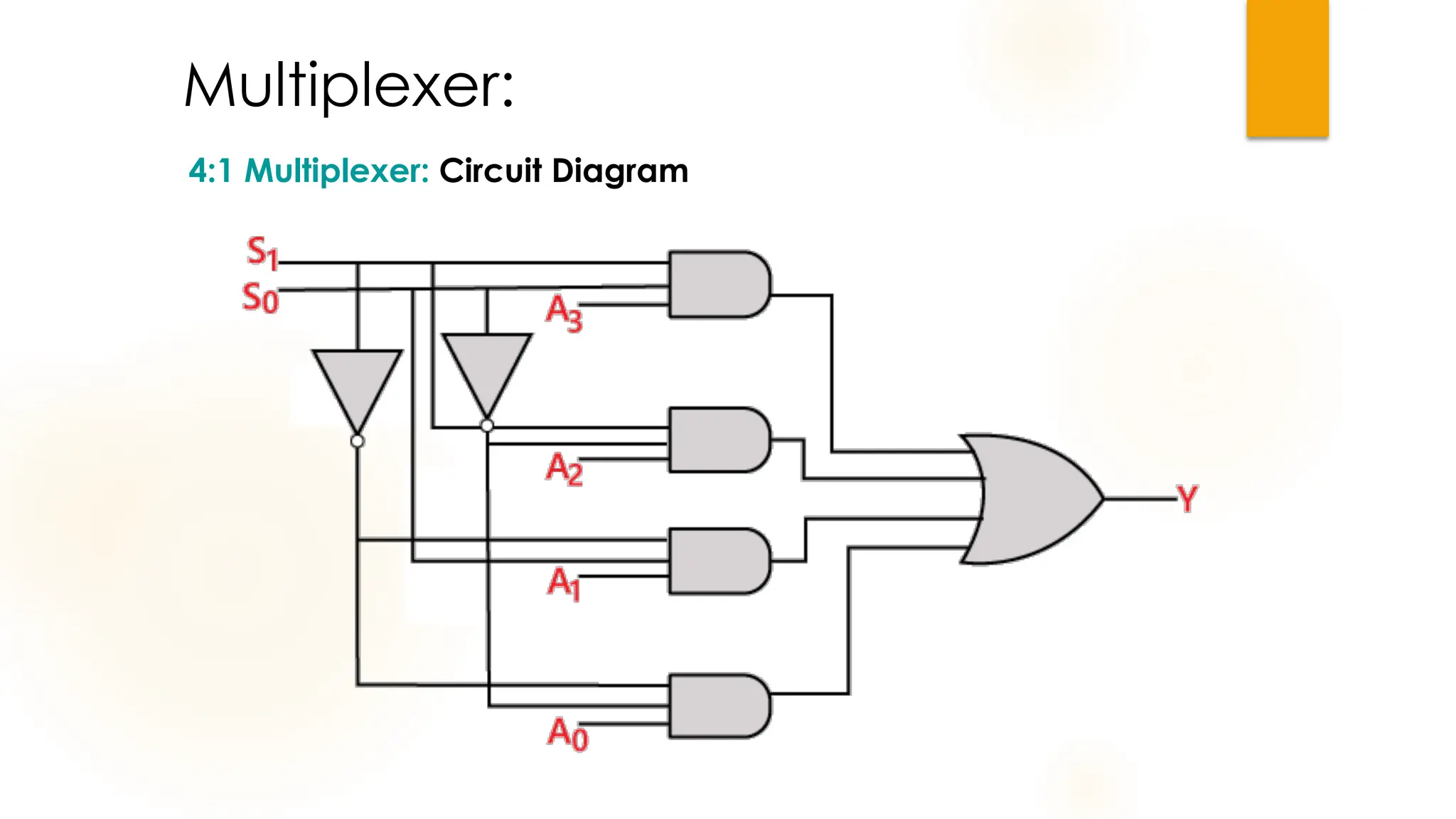
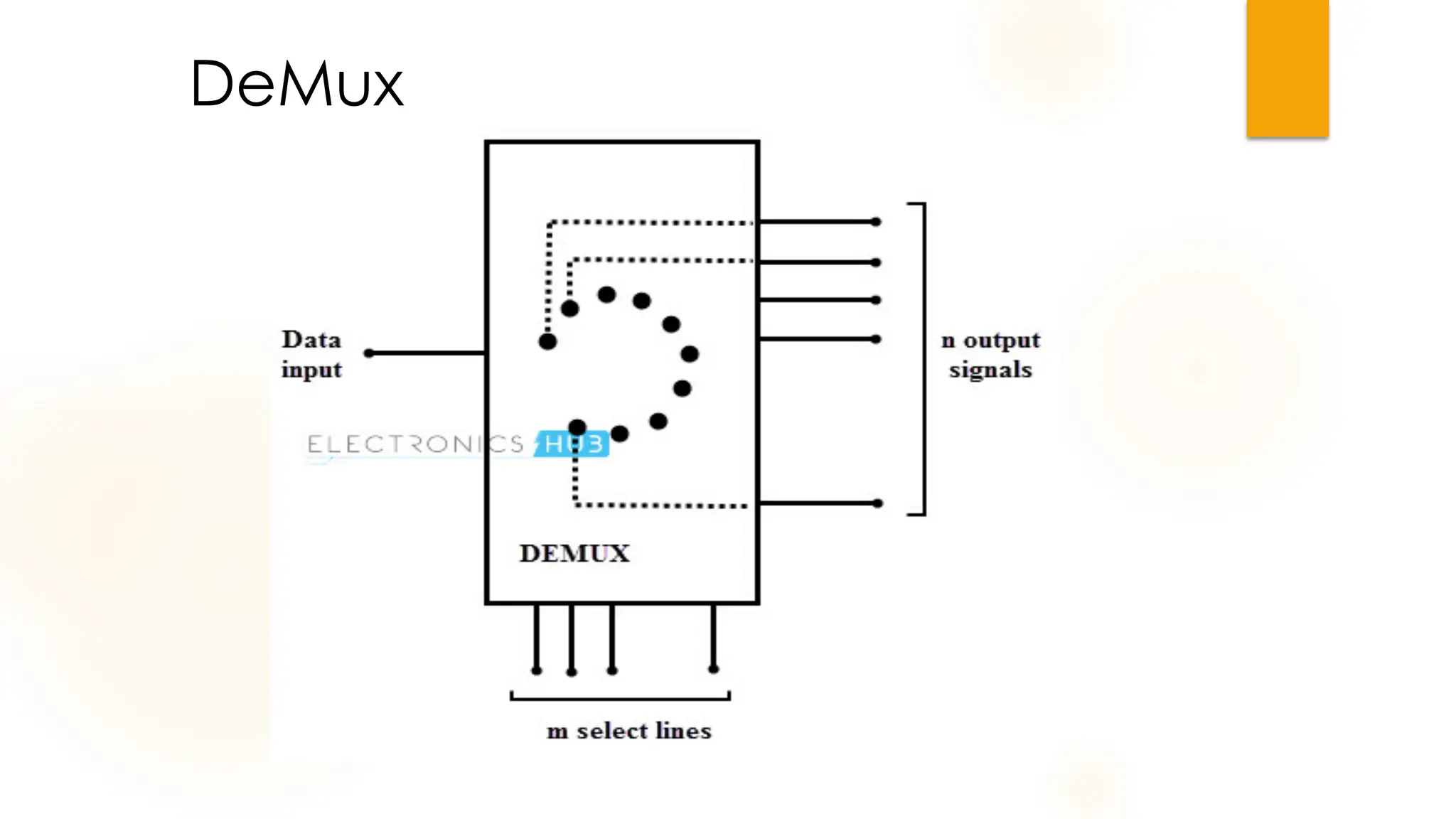
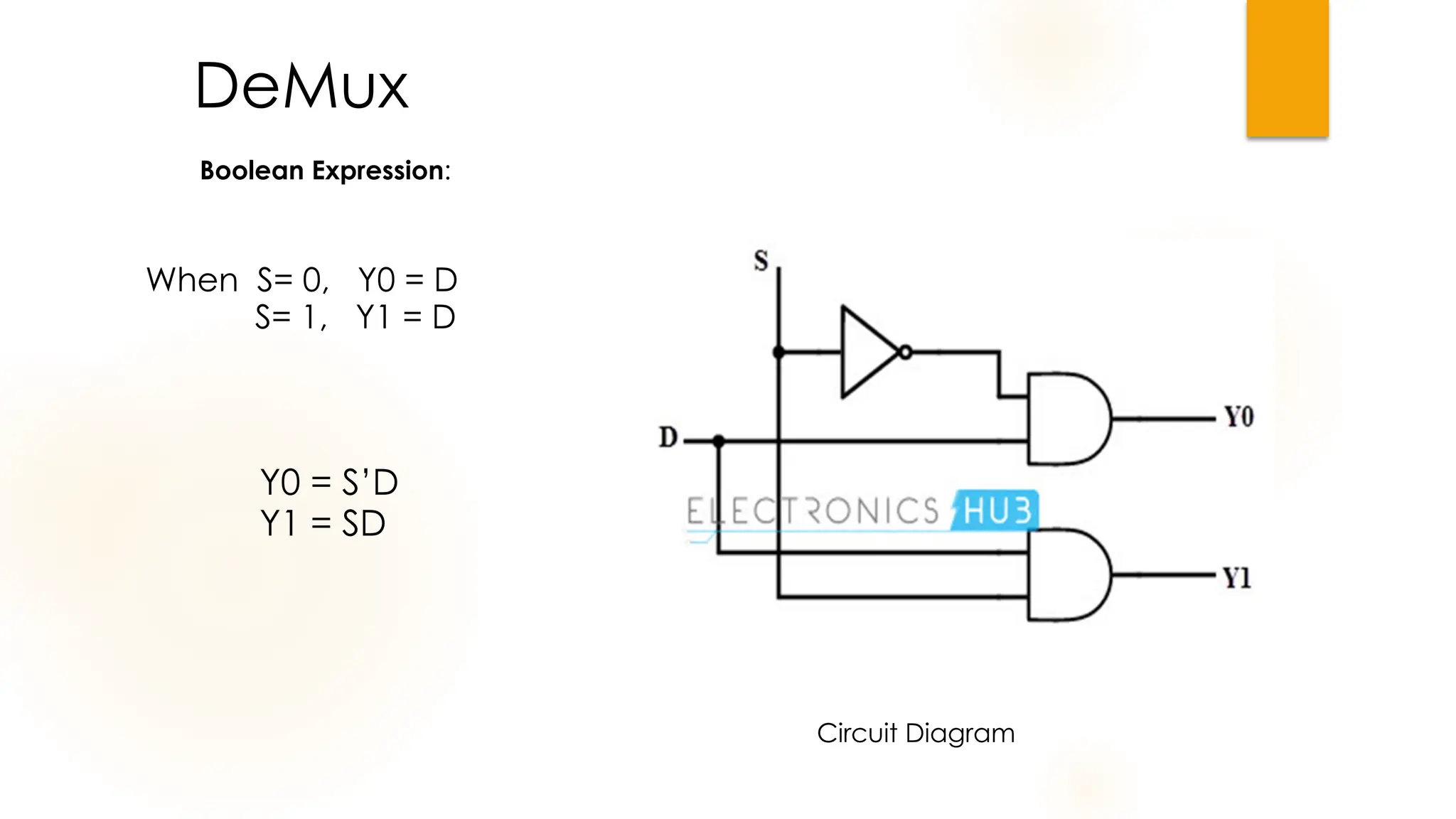
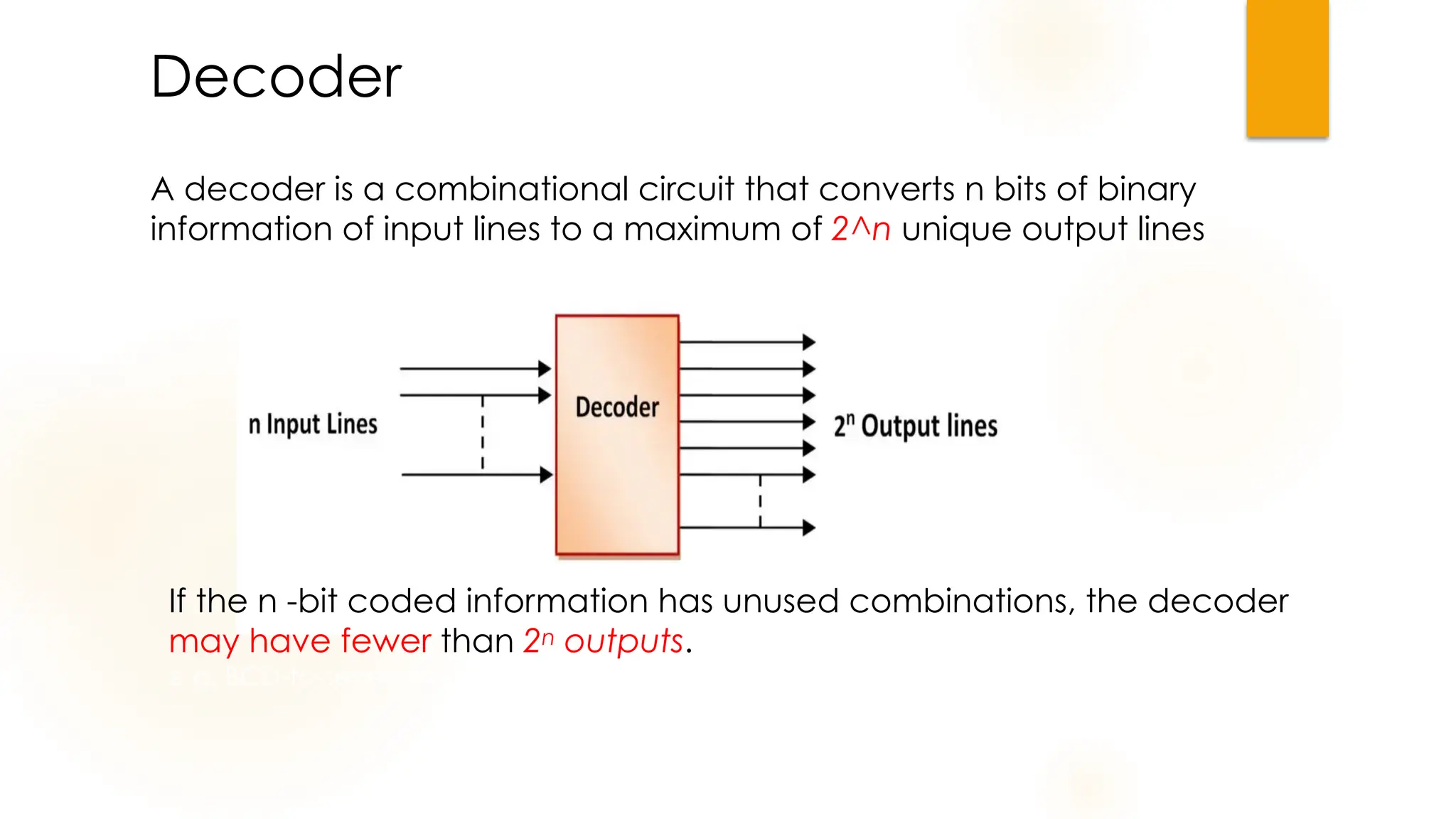
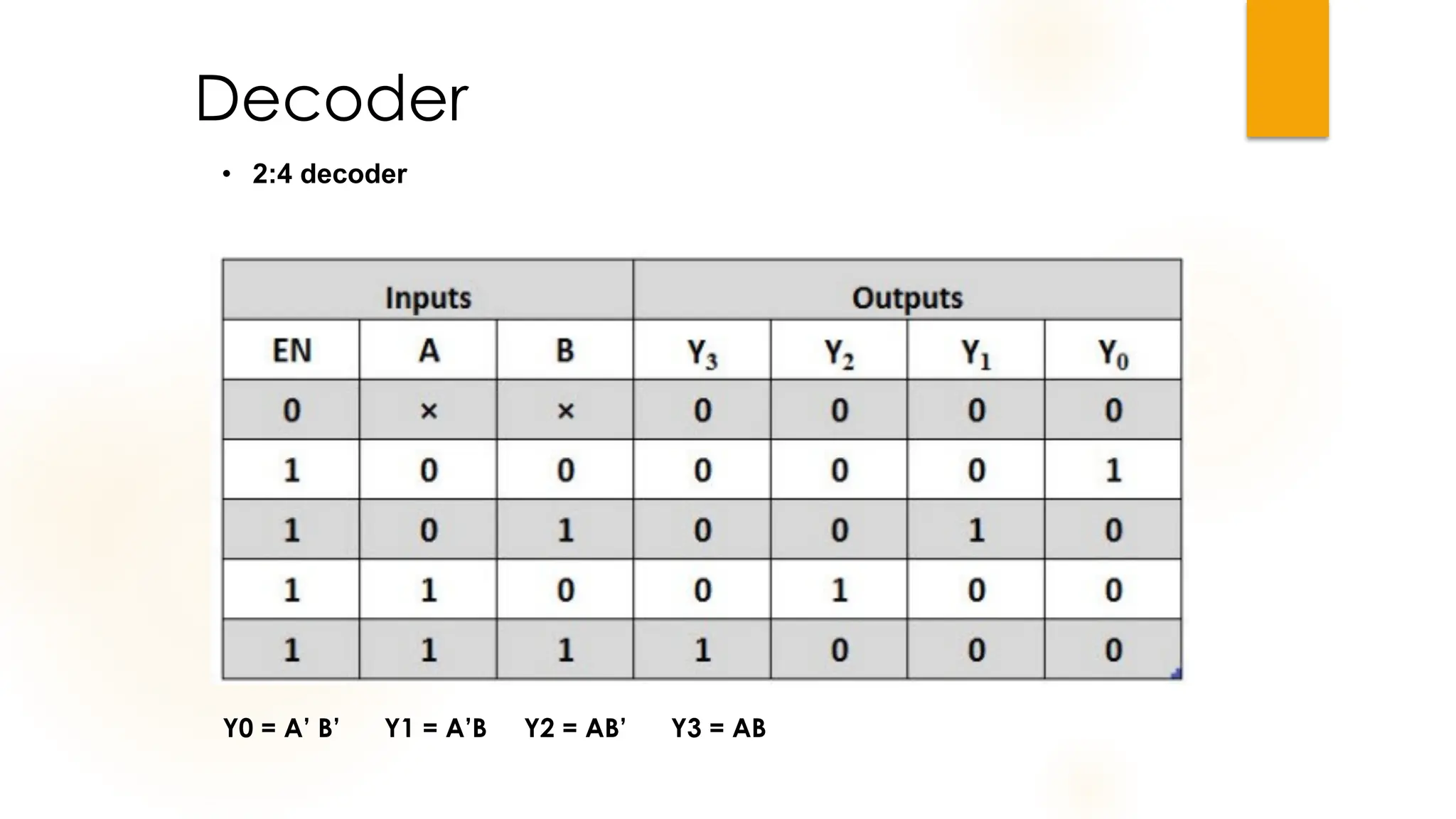
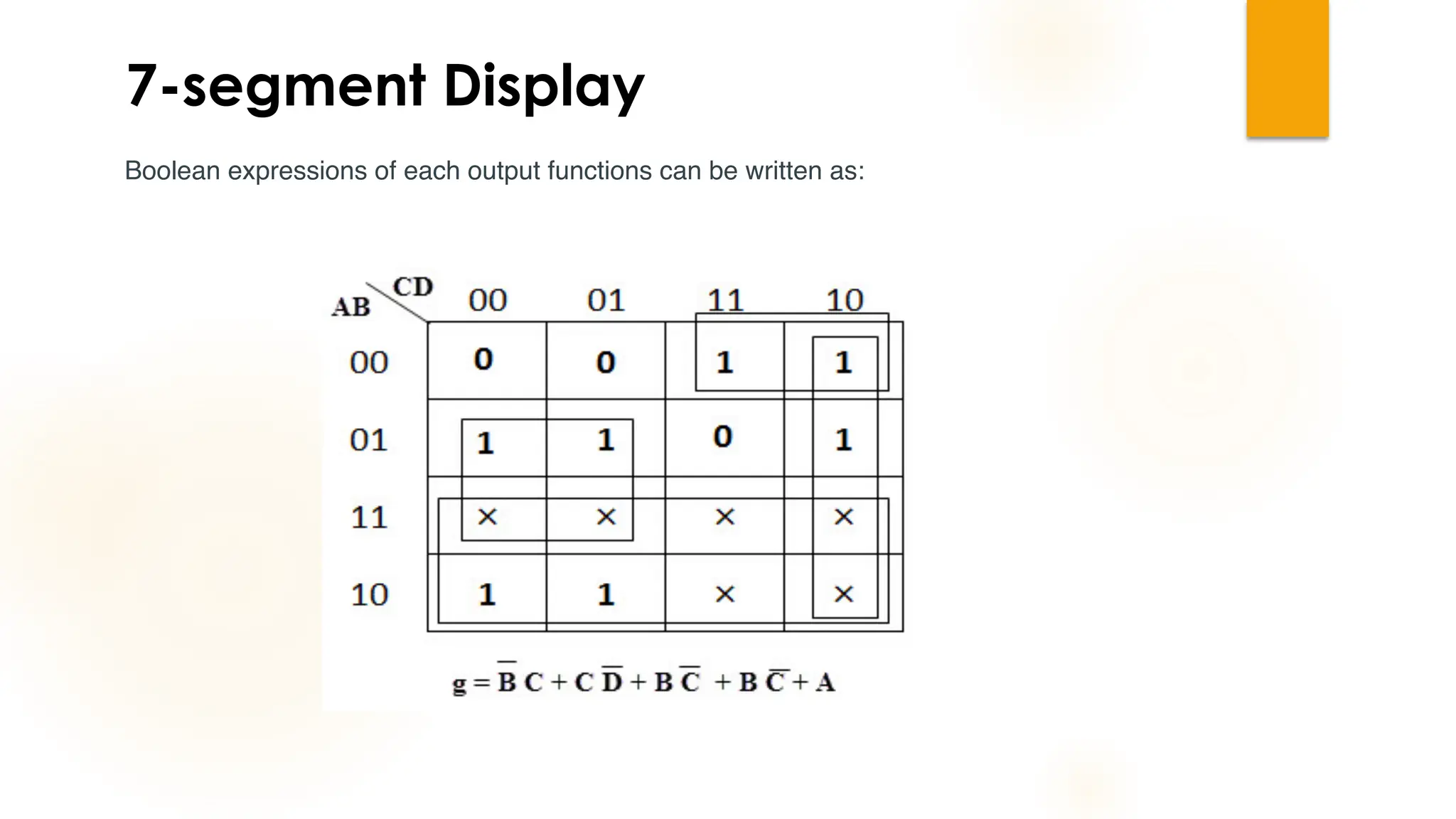
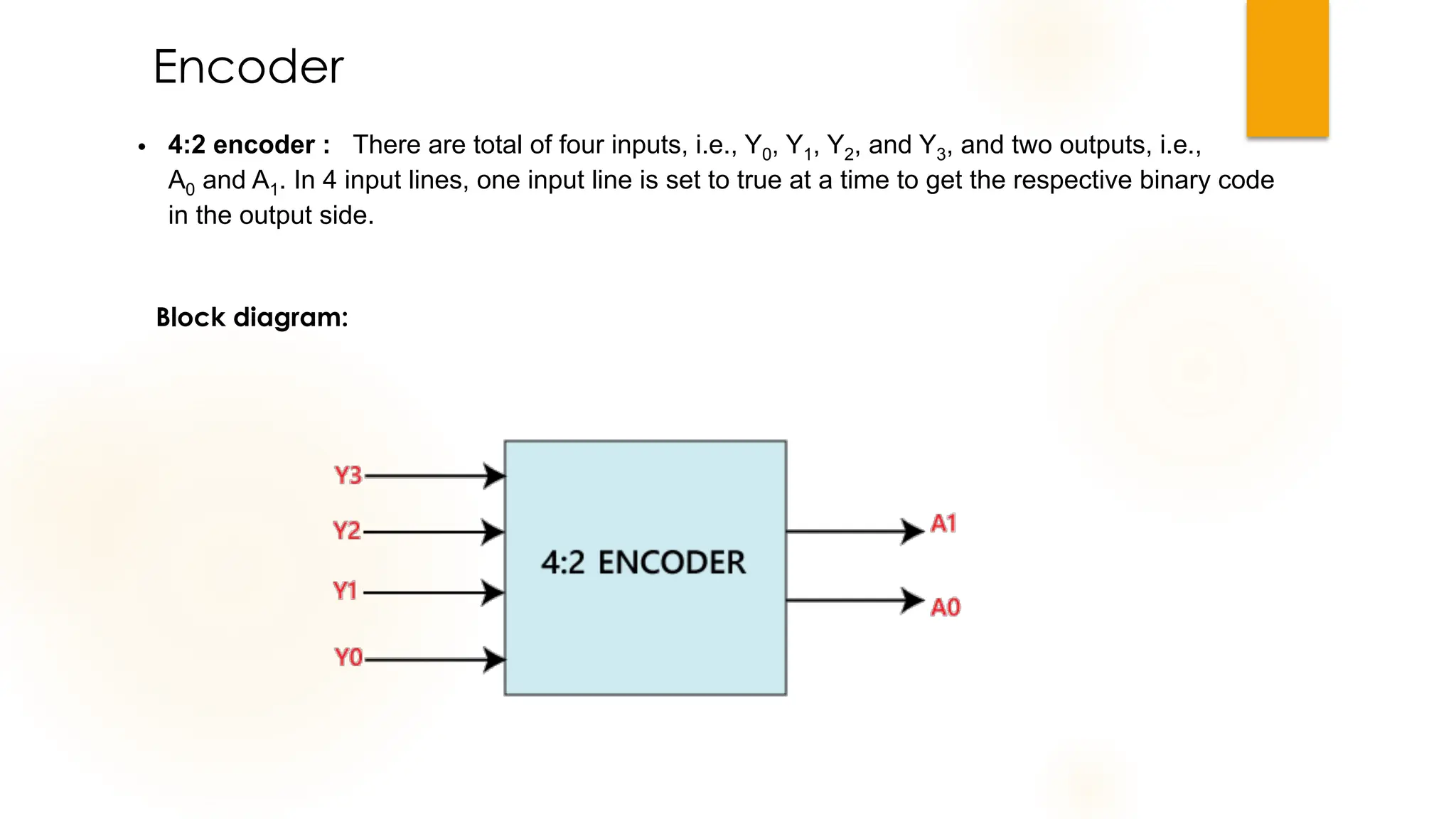
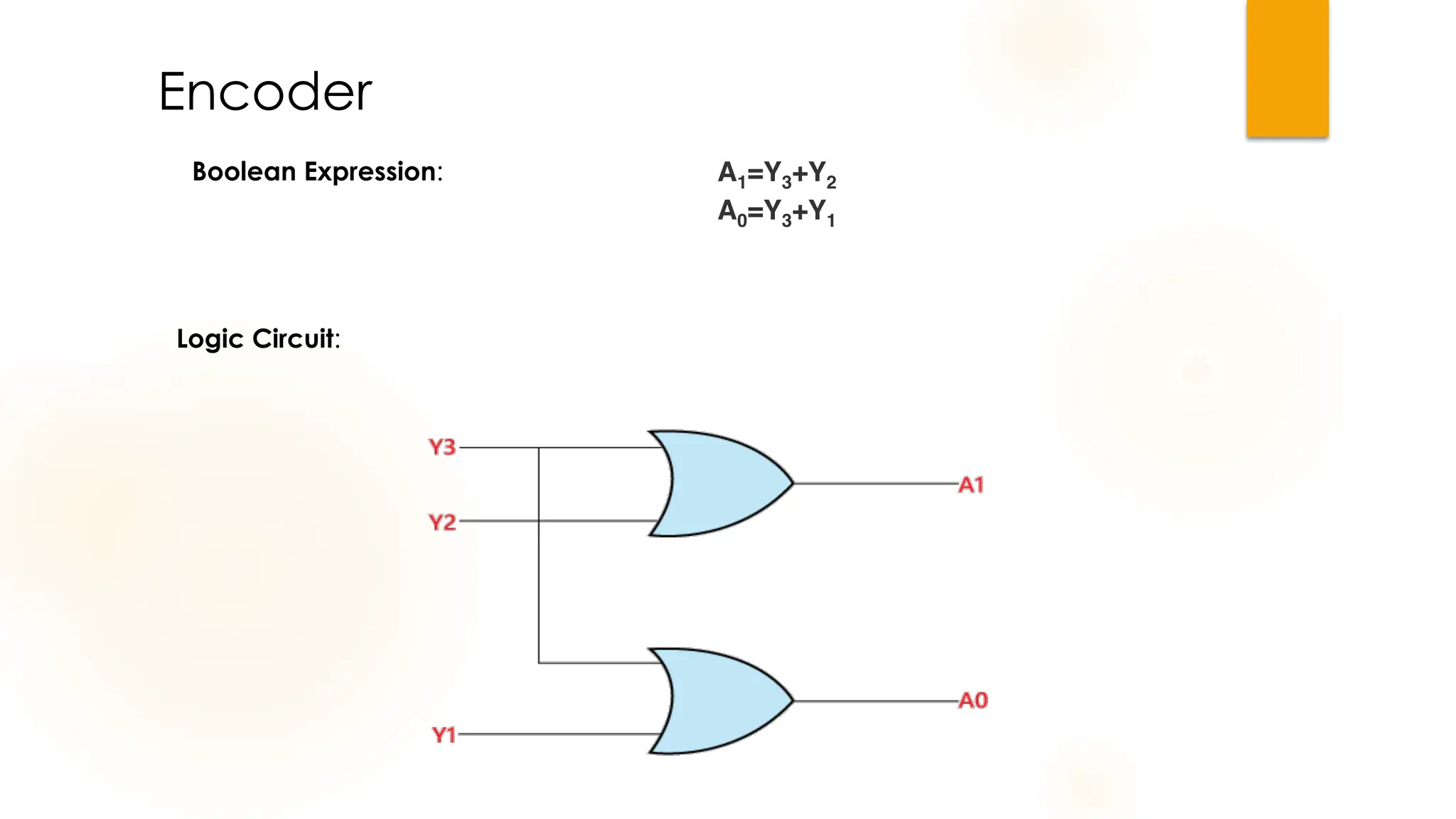
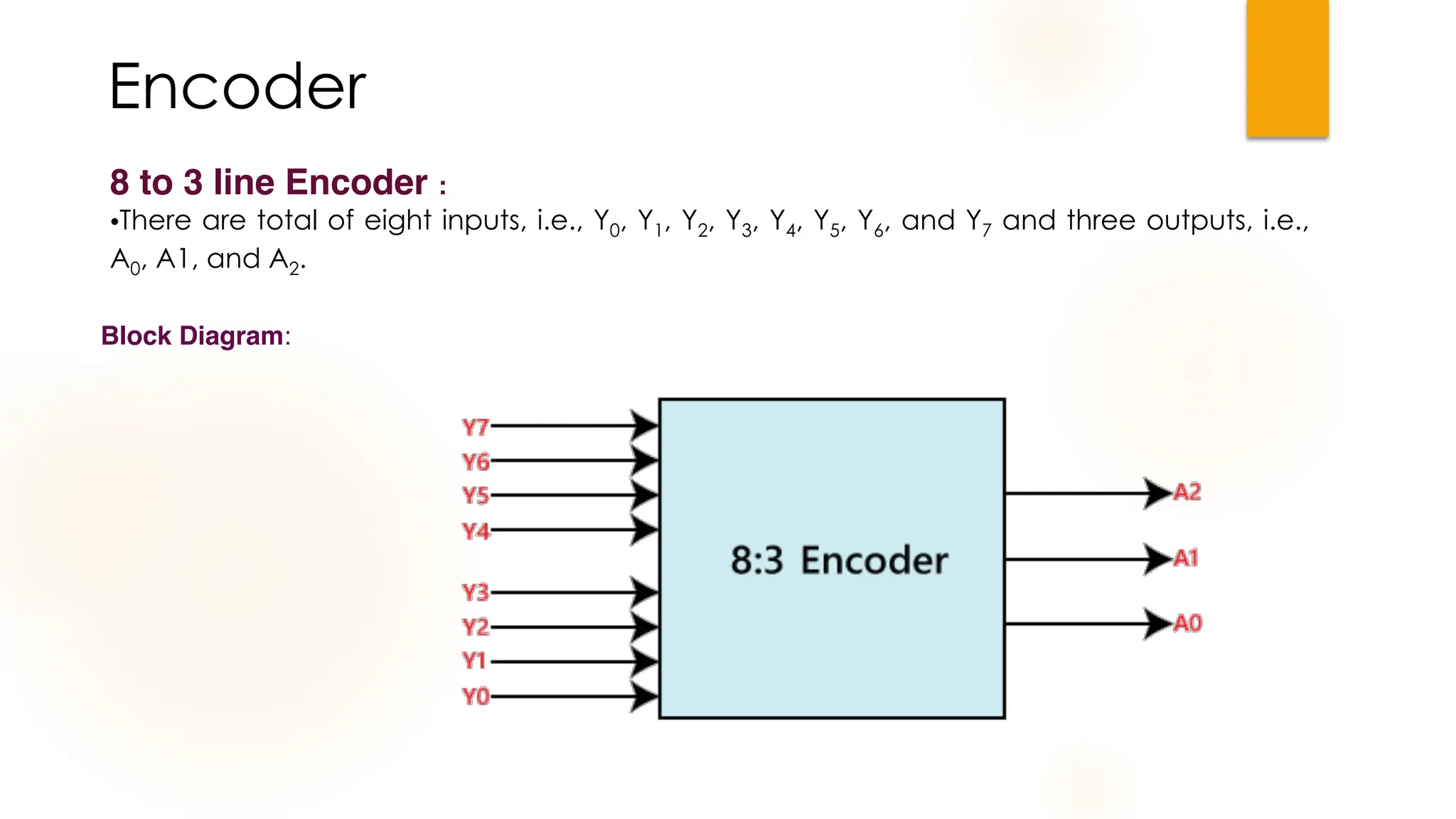
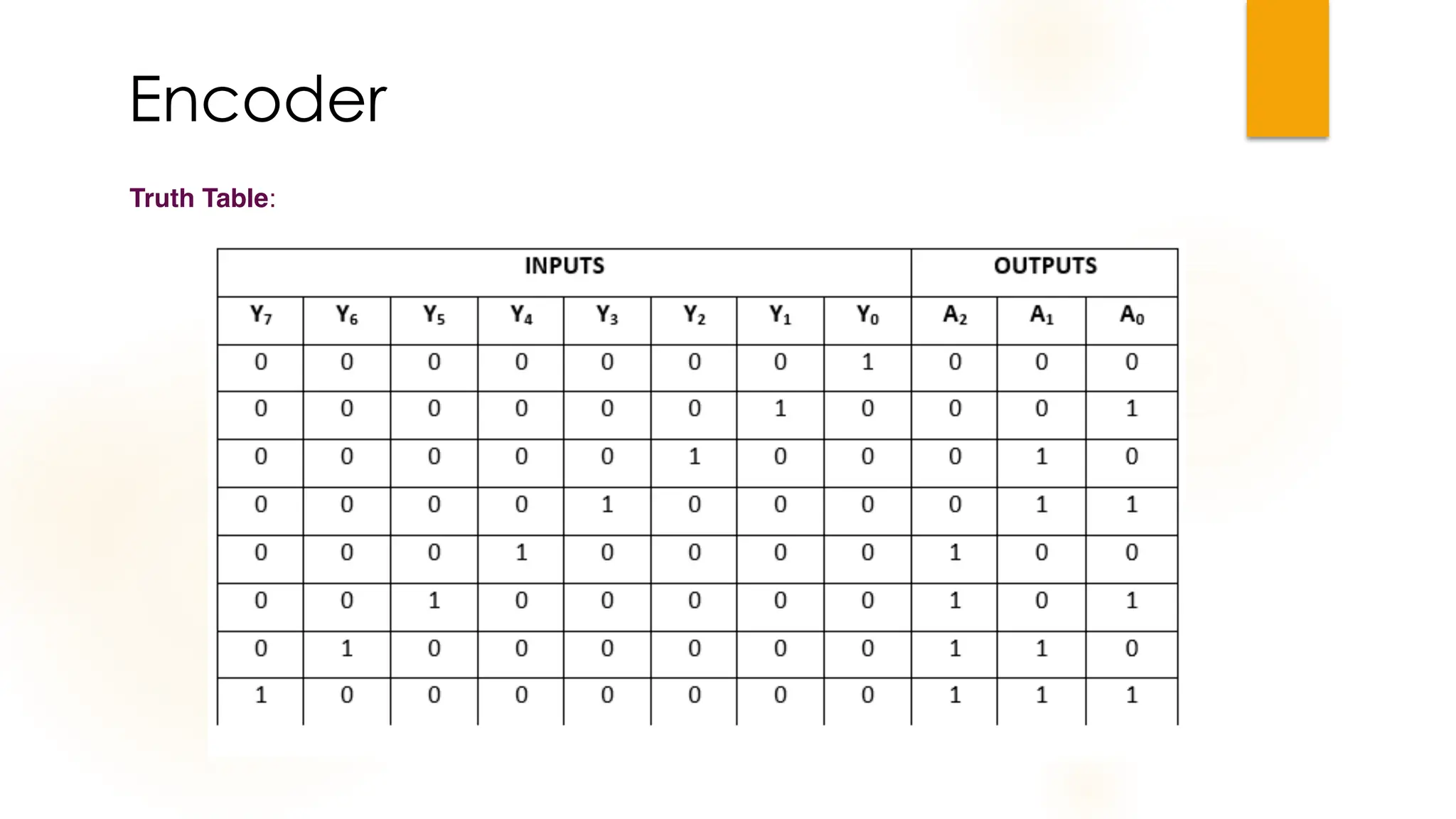
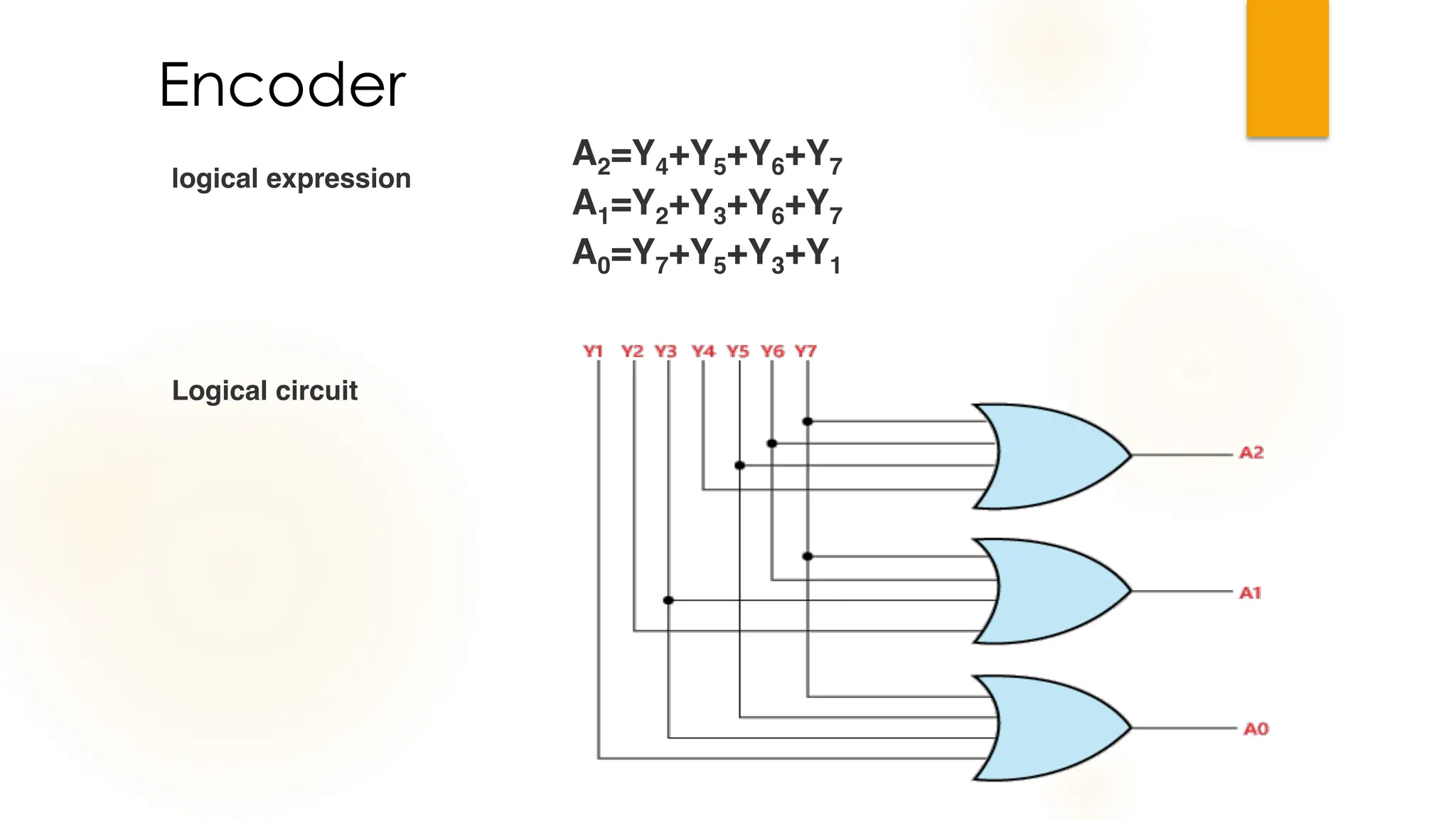
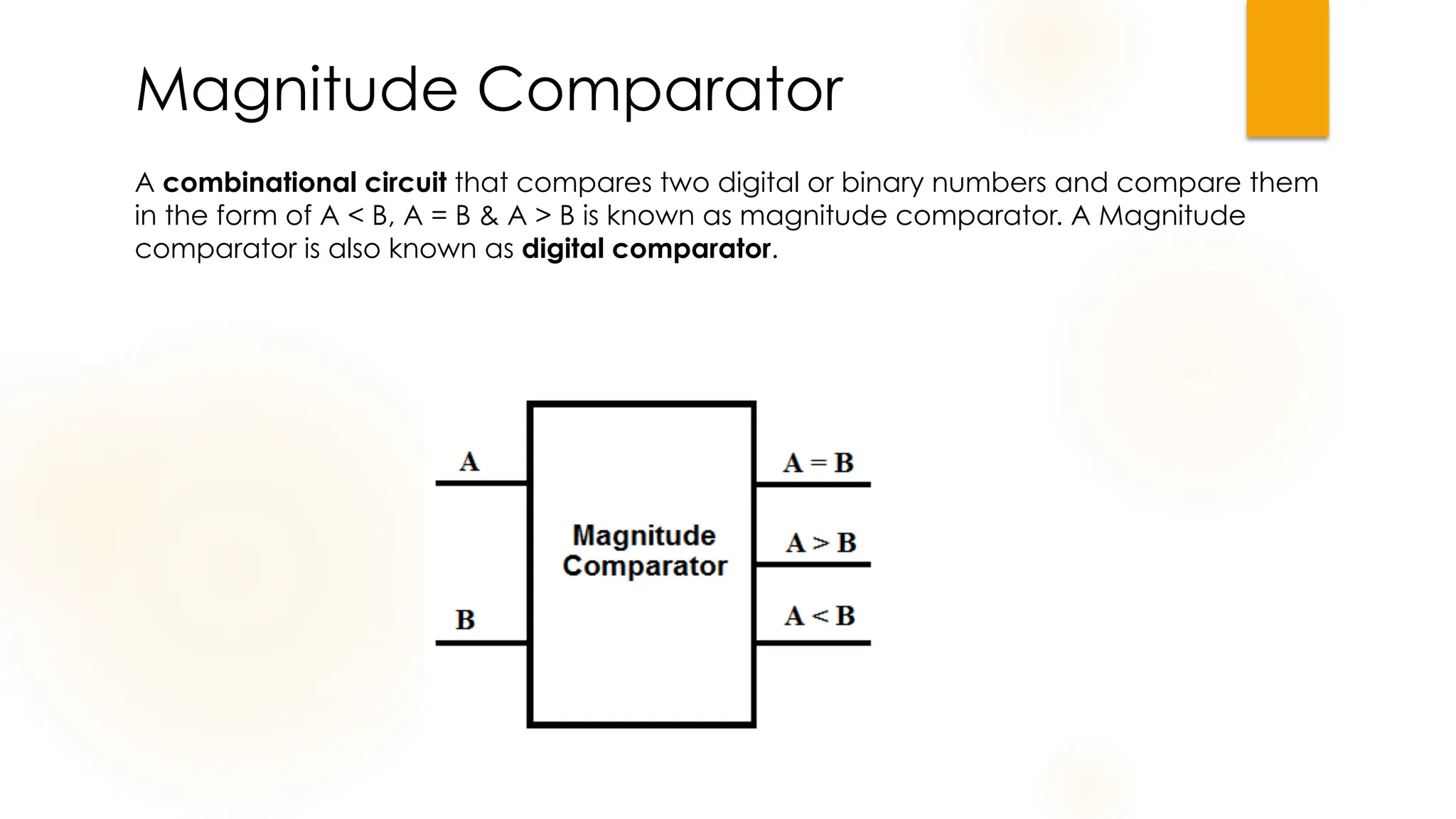
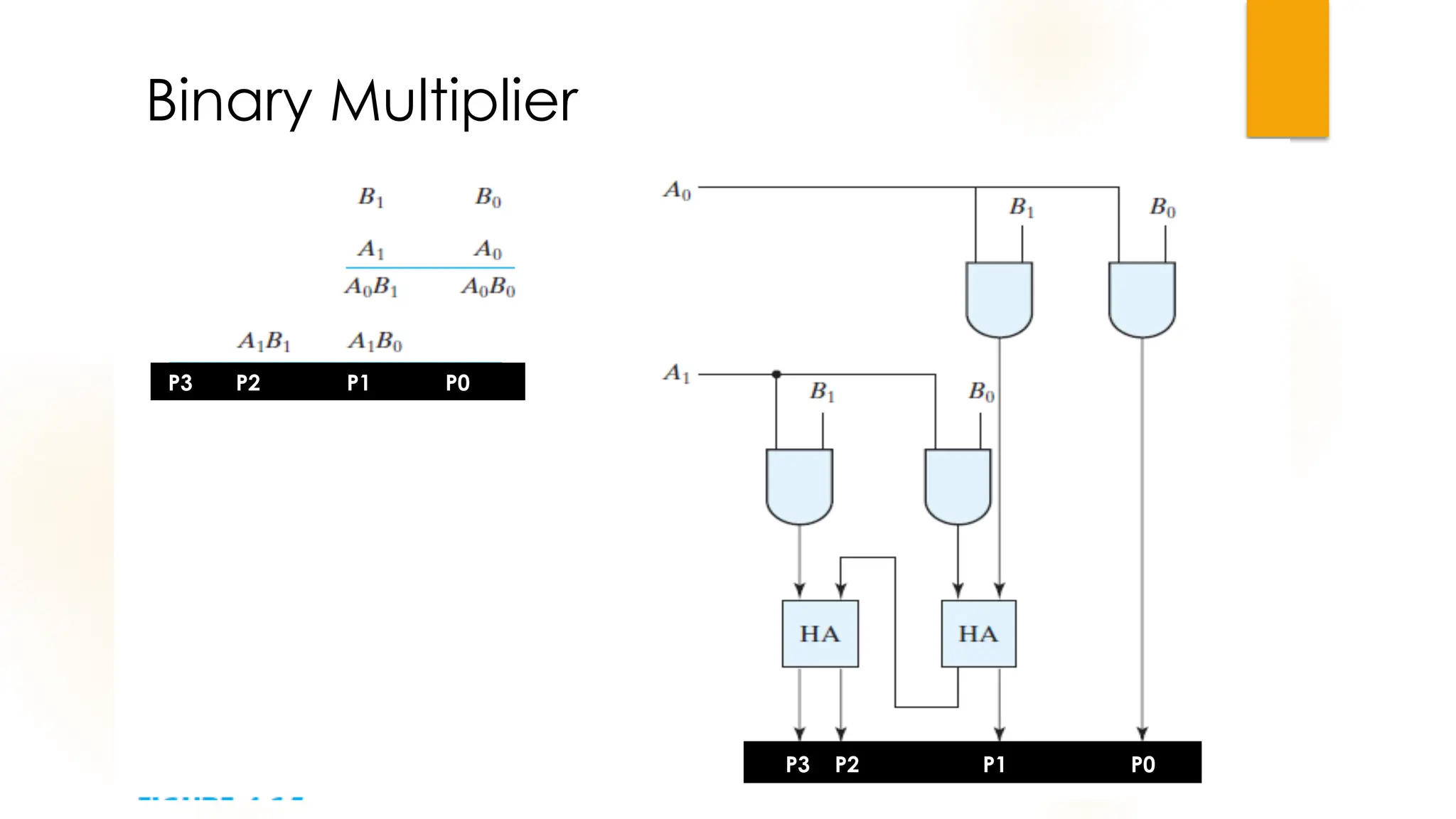
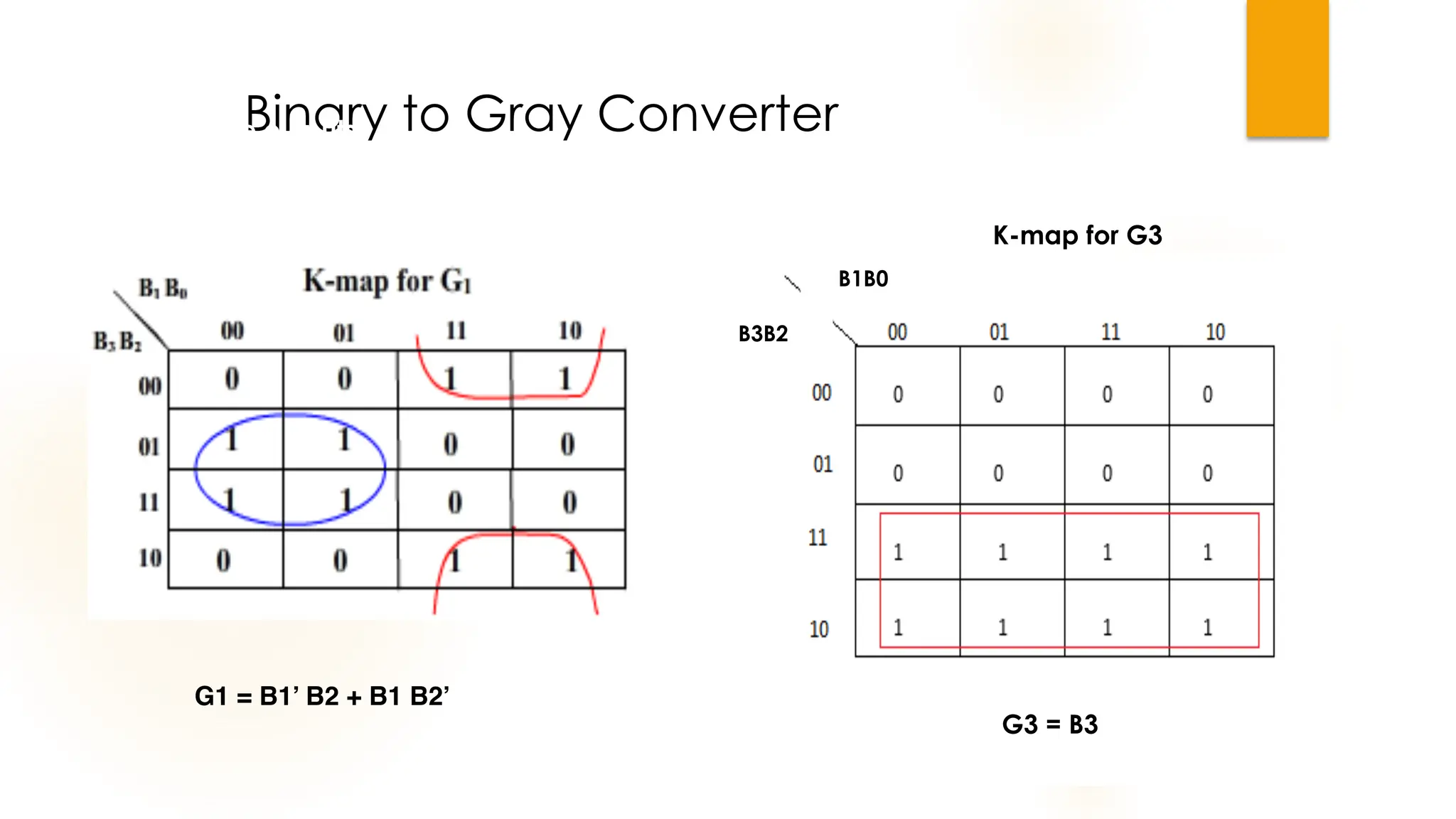
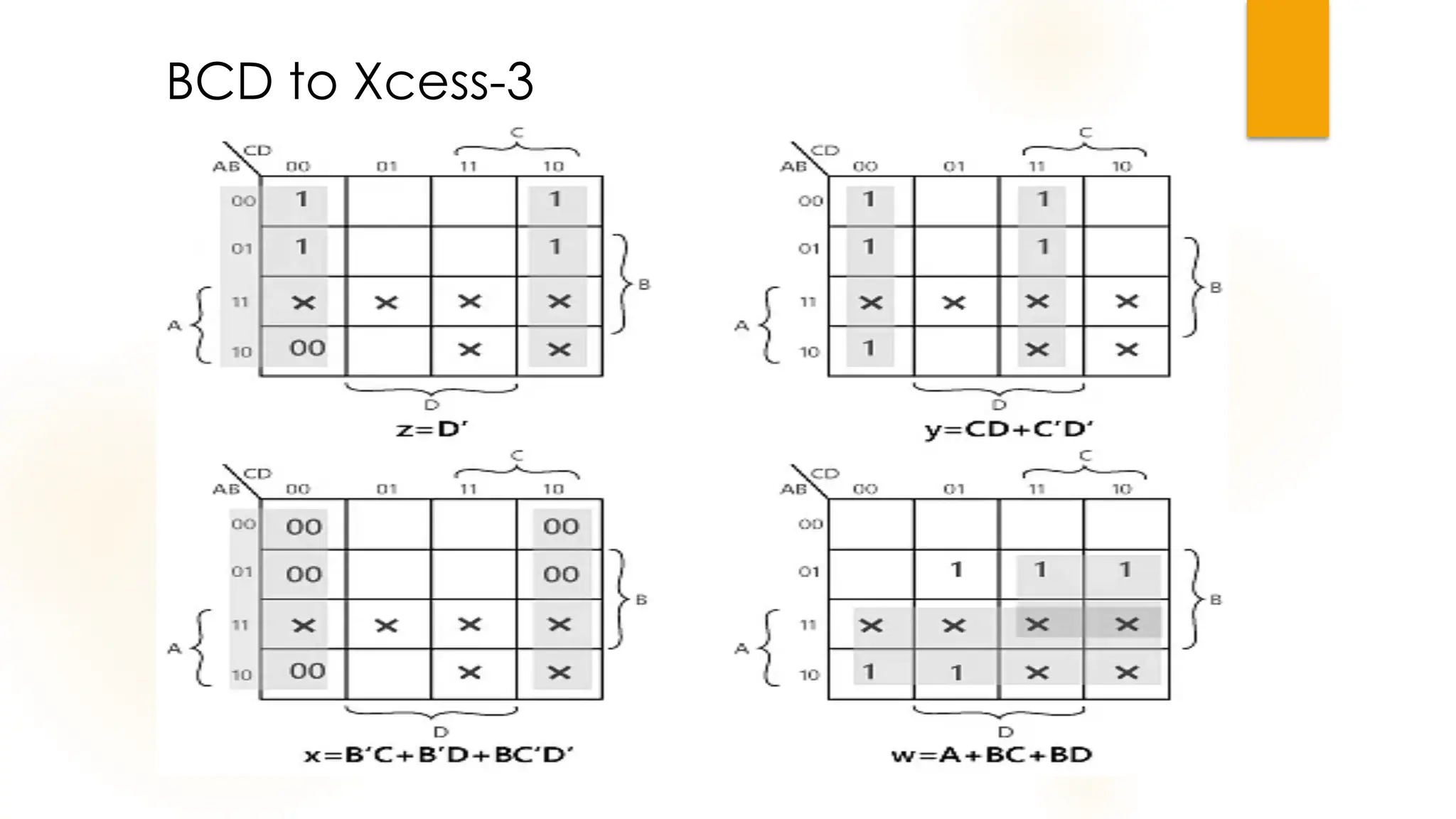
The document discusses combinational logic circuits, their characteristics, design procedures, and types including adders, subtractors, multiplexers, demultiplexers, encoders, and decoders. It outlines how to construct these circuits to perform specific functions, utilizing truth tables and boolean expressions for design. Additionally, it highlights applications of these circuits in digital systems and their operational principles.