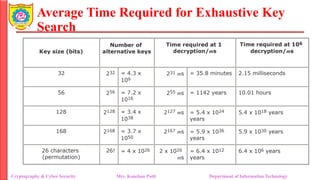
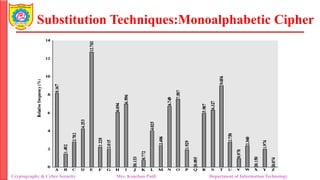
The document provides an overview of cryptography and cybersecurity fundamentals, focusing on symmetric encryption models, the processes of encryption and decryption, and various cipher techniques such as substitution and transposition. It details key concepts in cryptography like plaintext, ciphertext, and cryptanalysis, as well as different types of ciphers including the Caesar cipher, monoalphabetic ciphers, and the Playfair cipher. The document also discusses the significance of key security and the characteristics of cryptographic systems.
![Cryptography and Cyber Security
[IT311]
Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423603
(An Autonomous Institute Affiliated to Savitribai Phule Pune University, Pune)
NAAC ‘A’ Grade Accredited, ISO 9001:2015 Certified
Department of Information Technology
(NBAAccredited)
Mrs. Kanchan D. Patil
Assistant Professor](https://image.slidesharecdn.com/unit1classicalencryptiontechniques-250209173401-39757daa/85/Unit-1_Classical-Encryption-Techniques-pdf-1-320.jpg)





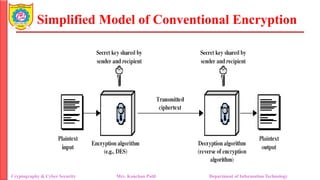

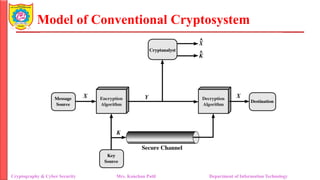
![Model of Conventional Cryptosystem
• Essential elements of a symmetric encryption scheme
• A source produces a message in plaintext, X = [X1, X2, ..., XM]
• The M elements of X are letters in some finite alphabet
• Traditionally, the alphabet usually consisted of the 26 capital letters
• The binary alphabet {0, 1} can also be used
• For encryption, a key of the form K = [K1, K2, ..., KJ] is generated
• If the key is generated at the message source, then it must also be
provided to the destination by means of some secure channel.
Alternatively, a third party could generate the key and securely
deliver it to both source and destination
Cryptography & Cyber Security Mrs. Kanchan Patil Department of Information Technology](https://image.slidesharecdn.com/unit1classicalencryptiontechniques-250209173401-39757daa/85/Unit-1_Classical-Encryption-Techniques-pdf-10-320.jpg)
![Model of Conventional Cryptosystem
• With the message X and the encryption key K as input, the encryption
algorithm forms the ciphertext Y = [Y1, Y2, ..., YN]
• We can write this as Y = E(K, X)
• This notation indicates that Y is produced by using encryption
algorithm E as a function of the plaintext X, with the specific function
determined by the value of the key K
• The intended receiver, in possession of the key, is able to invert the
transformation: X = D(K, Y)
Cryptography & Cyber Security Mrs. Kanchan Patil Department of Information Technology](https://image.slidesharecdn.com/unit1classicalencryptiontechniques-250209173401-39757daa/85/Unit-1_Classical-Encryption-Techniques-pdf-11-320.jpg)