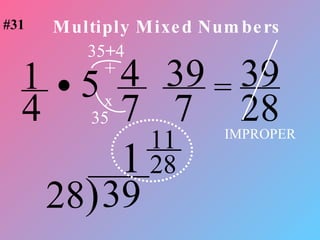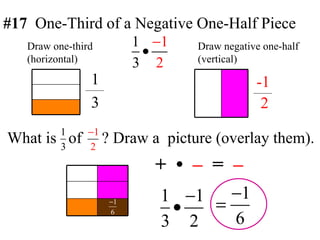
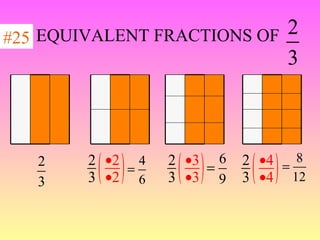
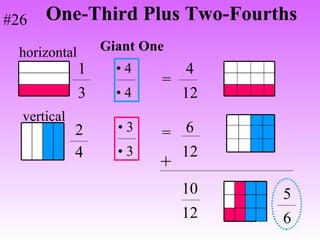
1) A mixed number has a whole number part and a fractional part, while an improper fraction has a numerator larger than the denominator. 2) To change between mixed numbers and improper fractions, you can multiply or divide the whole number by the denominator and add or subtract the numerator. 3) When adding, subtracting, multiplying or dividing fractions, you often need a common denominator or need to use reciprocals.

1. Mixed Number A mixed number has a part that is a whole number and a part that is a fraction. = 1 3 4 #1 An improper fraction is when the numerator is greater than the denominator. Improper Fraction 1/4 1/4 1/4 1/4 1/4 1/4 1/4 1/4 8 4 = numerator denominator

2. How To Change An Improper Fraction To A Mixed Number = 5 2 2 ) 5 numerator denominator 2 1 Divide the numerator by the denominator. Put your remainder over the denominator. 2 #2

3. How To Change A Mixed Number To An Improper Fraction 1) Multiply the whole number times the denominator. 2) Add your answer to the numerator. 3) Put your new number over the denominator. 4 1 2 x + = 9 2 #3

4. Decimals Terminating Decimal Is a decimal that stops. The decimal terminates if you reach a remainder of zero when you divide. Repeating Decimal Is a decimal that shows a pattern of repeating digits. #4

5. Decimal Place Value ___ , ___ ___ ___ ___ ___ ___ ___ Thousands Hundreds Tens Ones Ten ths Hundred ths Thousand ths Ten Thousand ths 2 4 3 1 6 Read as 243 and 16 hundredths #5 Decimals are read as “ and ”

6. To A Fraction : Read the decimal using the correct place value. How you say it determines the fraction. 0.2 TO CHANGE A DECIMAL #6 Two tenths

7. To a Decimal : Divide the numerator by the denominator. #7 TO CHANGE A FRACTION 3 4 3 4 0 . 7 2 8 2 0 0 5 20 0

8. #8 Writing Repeating Decimals as Fractions

9. Equivalent Fractions Equivalent fractions name the same amount or the same part of a whole. You use the giant one to show equivalent fractions. Example: #9 A fraction shows: Parts Shaded Total Parts Numerator Denominator

10. Least Common Denominator TO FIND THE LCM OF 4 and 12: 2) Find the least multiple that both numbers have in common. 1) List the multiples of both numbers 4 = 4, 8, 12, 16, 20… 12 = 12, 24, 36… LCM is 12 #10 Least Common Multiple is also known as LCD.

11. < Less than > Greater than Less than or equal to Greater than or equal to Read these symbols from left to right. **************************************************************** C o m p a r i n g F r a c t i o n s #11 To compare fractions you must show your work ! >

12. Steps for Rounding Find the number. Circle it. Look next door. 4 or less just ignore. 5 or more add one more. Example : Round 5.328 to nearest hundredth . Circle the 2 in the hundredths place. Look next door at the 8. It is 5 or more so add 1 more to the hundredths place. 5.328 rounds to 5.33 # 12

13. Add Decimals Add 3.41 + 2.5 1 Step 1: Line up the decimals 3.41 + 2.5 Step 2: If needed, put zeros in as place holders Step 3: Add decimals Step 4: Bring decimal down . 0 #13 9 5

14. Subtract Decimals Subtract 3.58 – 1.6 8 Step 1: Line up the decimals 3.58 - 1.6 Step 2: If needed, put zeros in as place holders Step 3: Subtract decimals Step 4: Bring decimal down . 0 #14 2 1 9 1

15. -2 6 3 6 1 + You ADD numerators The denominator STAYS THE SAME ! Add Fractions With The Same Denominator #15 6

16. Giant One/ Simplest Form The Giant One is used to reduce or simplify fractions . #16 To find the simplest form divide the numerator and denominator by the greatest common factor.

17. Draw one-third (horizontal) Draw negative one-half (vertical) 1 3 -1 2 What is of ? Draw a picture (overlay them). #17 One-Third of a Negative One-Half Piece + • – = –

18. Multiply 4 3 7 2 = 28 6 6 ) 28 4 24 4 = 2 3 4 You do NOT need common denominators  Multiply the numerators and denominators straight across. #18 Change the improper fraction to a mixed number 4 6 ÷ ÷ 2 2 Reduce! 4 4 6

19. Multiplying Decimals Steps for Multiplying Decimals Step 1: Write the problem vertically. Step 2: Ignore the decimal point(s) and multiply. Step 3: Determine where the decimal point goes in the product. Place the decimal point in the answer by counting how many places the decimal point has moved. #19

20. Divide 3  1) Draw a picture to show 3 wholes. 2) How many ’s fit into 3 wholes? There are 12 one-fourths that fit into 3. 1 2 3 4 5 6 7 8 9 10 11 12 #20

21. Reciprocals = Example: - - X 2 2 5 5 - = 1 10 10 To find the reciprocal just flip the fraction over. #21 Two numbers are reciprocals if their product is one. Change your mixed number to an improper fraction to find the reciprocal. 5 2 3 x + = 17 3 3 17

22. Dividing Fractions Example: 5 - 6 - 2 - . . 3 = - 5 6 X - 3 2 = 1 2 - 5 4 = 1 - 1 4 . To divide fractions, multiply the first fraction by the reciprocal of the second fraction. #22

23. NO decimal point in the divisor. Divide 0.27  3 3 0. 27 . 0 0 0 2 7 9 27 0 #23 Divisor Dividend Step 2: Move the decimal point in the dividend straight up into the quotient Step 3: Divide as usual Step 1: Write the problem in the long division format TRICK: D ead M onkeys S mell B ad !

24. Divide Decimals Step 2: Move the decimal point in the divisor to the far right of the divisor Step 5: Divide as usual Step 1: Write the problem in the traditional long division Divide 0.42  0.6 0 6 0 4 2 . 0 0 0 4 2 7 42 0 Step 3: Move the decimal point the SAME NUMBER of places in the dividend Step 4: Move the decimal point in the dividend straight up into the quotient . . . . #24 Dividend  Divisor Yes, decimal point in the divisor.

25. EQUIVALENT FRACTIONS OF #25

26. One-Third Plus Two-Fourths #26 horizontal vertical 1 3 2 4 • 4 • 4 Giant One • 3 • 3 4 12 6 12 10 12 + 5 6 = =

27. Add Fractions 4 5 -2 3 + 15 15 x 5 = x 3 = x 5 = x 3 = -10 12 2 15 Find a common denominator . 2) Add the numerators. 3) Keep the common denominator the same. #27 4) Simplify or reduce. Change improper fractions to mixed #s.

28. Subtract Fractions 5 6 1 8 - 24 24 x 3 = x 4 = x 3 = x 4 = 3 20 17 24 Always SHOW YOUR WORK ! This includes the Giant One. #28 Giant One

29. Add Mixed Numbers 5 6 5 8 + 24 24 x 3 = x 4 = x 3 = x 4 = 15 20 35 24 24 3 24 ) 35 1 11 11 24 24 1 28 11 24 #29 IMPROPER

30. Subtract Mixed Numbers 1 st : Change your mixed numbers to improper fractions . 2 7 6 7 - 7 7 13 30 17 7 4 1 = = 2 nd : Subtract numerators. 3 rd : The denominator stays the same. 4 th : Change your answer to a mixed number. 7 ) 17 2 14 3 7 3 #30

31. Multiply Mixed Numbers 1 4 = 4 7 x 35 35 + 4 5 + 39 7 39 28 28 ) 39 1 11 28 #31 IMPROPER

32. FRACTION REVIEW Add Fractions: Find a common denominator. Add the numerators, and keep the denominator the same. Subtract Fractions: Find a common denominator. Subtract the numerators, and keep the denominator the same. Multiply Fractions: Multiply the numerators and denominators straight across. Divide Fractions: Multiply the first fraction by the reciprocal of the second fraction. Mixed Numbers: Change it to an improper fraction first. #32