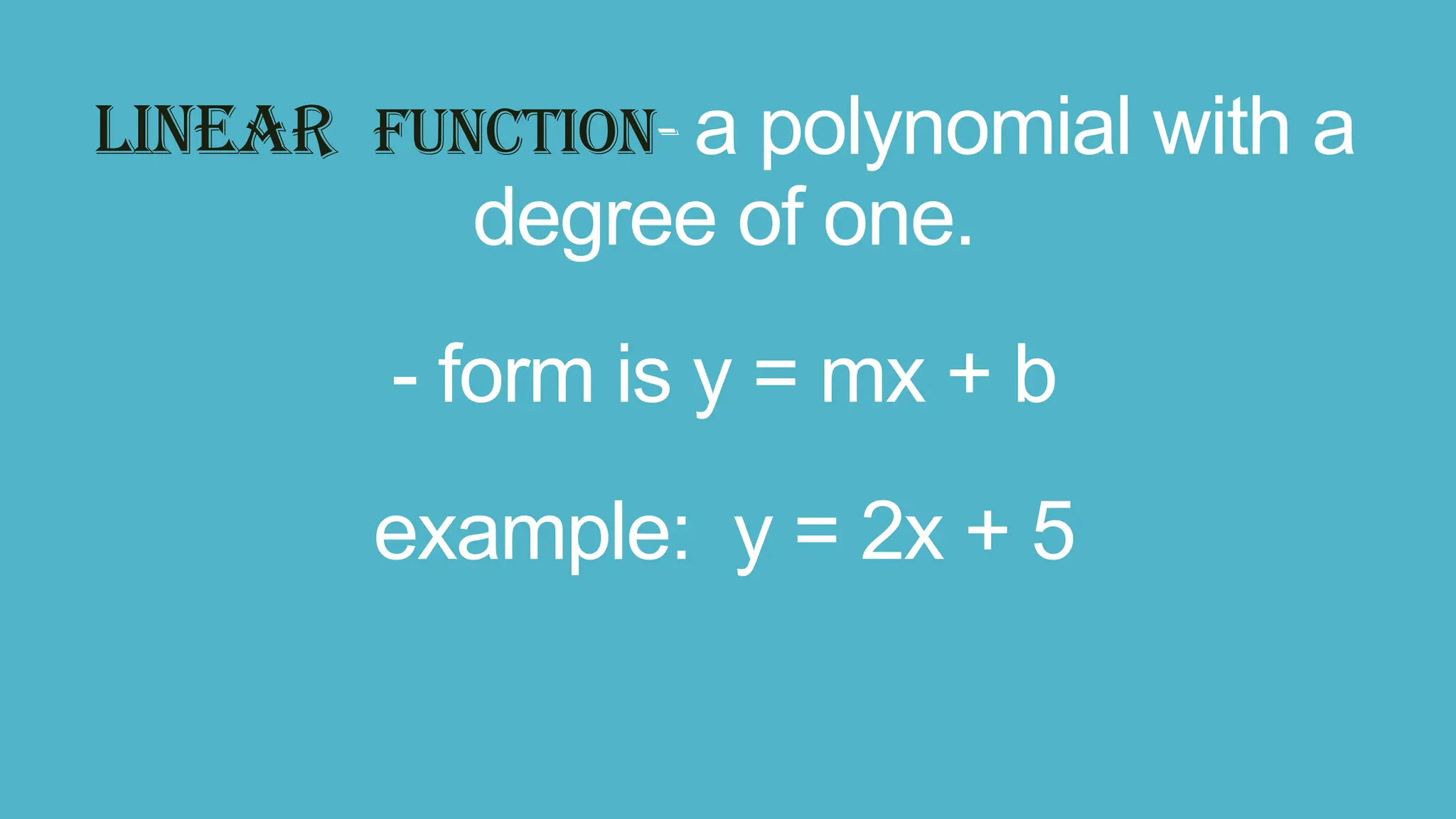The document outlines various types of functions in mathematics, including constant, identity, linear, quadratic, cubic, power, rational, exponential, and logarithmic functions. Each type is defined with its standard form and an example. These functions vary by degree and characteristics, such as growth behavior in exponential functions.

1. TYPES OF FUNCTION

2. Constant function- function that has
the same output value no matter what
your input value is.
-form f(x) = b , where b is a constant
example: y= 7

3. identity function- function which
returns the same value which was used
as argument.
example: f(2) = 2

5. Linear function- a polynomial with a
degree of one.
- form is y = mx + b
example: y = 2x + 5

6. quadratic function- a polynomial with
a degree of two.
y= a + bx + c, where a, b and c are
constant, a ≠ 0 and x is a variable.
example: y= 4x – 10

7. cubic function- a polynomial with a
degree of three.
y= a + b + cx + d, where a, b, c and d
are constant, a ≠ 0 and x is a variable.
example: y= 5 + 3 + 2x + 5

8. Power function- a function in the form
y= a.
- linear and quadratic are power
function
example: f (x) = 8

9. Rational Function- is any function which can be
represented by a rational fraction say,
q(x )
p(x )
in which numerator, p(x) and denominator, q(x) are
polynomial functions of x, where q(x) ≠ 0.
example:
- 4

10. Exponential
function- These are functions of the form:
y= a,
where x is in an exponent and a and b are
constants. (Note that only b is raised to
the power x; not a.) If the base b is greater
than 1 then the result is exponential
growth.
example: y =

11. Logarithmic Function: are the inverses
of exponential functions, and any
exponential function can be
expressed in
logarithmic form.