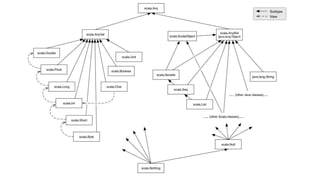
Scala has a static, strong, and Turing complete type system that can infer types. It supports object-oriented programming with named types like Dog and functional programming with parameterized types like List[Int]. New types can be defined through classes, traits, case classes, and type members. Types are more general than classes and include structural types. Variance controls subtype relationships for parameterized types. Type bounds and existential types provide additional type safety. Higher kinded types allow types to be parameterized over other types.

1. Types in Scala
({type λ[-α]= T[α] <~< T[A2]})#λ

2. A bit of history
Type theory – invented by Russel in 1903 to prevent Russel’s paradox
Idea: limit the expressive power and disallow inconsistencies

3. Scala type system
• is static
• is strong
• can infer types
• is unified
• is Turing complete

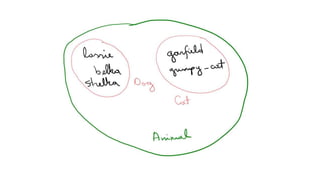
4. In a nutshell
OOP/modular
• named BitSet
• compound Channel with Logged
• refined Channel {def close(): Unit }
Functional
• parametrized List[Int]
• existential List[T] forSome {type T}
• higher-kinded List[_]

6. Declaring types
scala> val y: Int = 1 // explicit type declaration
y: Int = 1
scala> val x = 1 // type inference
x: Int = 1
scala> def double(i: Int): Int = i * 2
double: (i: Int)Int // type of method
// (technically not the same as a function)

7. Defining new named types
scala> class Animal
scala> class Dog extends Animal
scala> class Cat extends Animal
scala> val lassie: Dog = new Dog
scala> val garfield: Cat = new Cat
scala> val garfieldAnimal: Animal = garfield

9. Algebraic Types
• These are “data-only” types, i.e. case classes
• Pattern match to deconstruct them
scala> case class Person(name: String, id: Int)
defined class Person

12. There is only one value of Null
scala> val n: Null = null
n: Null = null
scala> val n: Null = garfield
<console>:10: error: type mismatch;
found : Cat
required: Null
val n: Null = garfield
^

13. There are no values of Nothing !
scala> val nothing: Nothing = throw new Exception("die")
java.lang.Exception: die
... 33 elided

14. Traits
scala> trait Cosmic {
def flyToSpace: Unit
def flyTwice: Unit = { flyToSpace; flyToSpace } // Can contain implementations!
}
defined trait Cosmic
scala> class SpaceDog extends Dog with Cosmic {
def flyToSpace = println("flying!")
}
defined class SpaceDog

15. Trait linearization
class Animal
trait Furry extends Animal
trait HasLegs extends Animal
trait FourLegged extends HasLegs
class Cat extends Animal with Furry with FourLegged
reverse –> expand –> right-keep-unique -> add-common

16. Type refinement
scala> val laika = new Dog with Cosmic { // type refinement !
def flyToSpace = println("done!")
}
scala> laika.flyToSpace
done!

17. Types ≠ Classes
Key idea: A type is a broader concept than a class !
Type declarations are NOT ONLY class declarations!
scala> def eatInSpace(a: Edible with Cosmic) = println("om nom nom!")
eatInSpace: (a: Edible with Cosmic)Unit

18. Anonymous and Structural types
scala> val xz = new { def act = println("acting!") }
xz: AnyRef{def act: Unit} = $anon$1@74224c87
scala> def act(a: { def act: Unit }) = a.act
act: (a: AnyRef{def act: Unit})Unit
scala> act(xz)
acting!

20. Type Parameters
scala> class MyList[T]
defined class MyList
scala> val x = new MyList[Int]
scala> val y = new MyList[String]

21. Tuples and Unit
scala> val x: Tuple2[Int, String] = (1, "abc")
x: (Int, String) = (1,abc)
scala> val x: (Int, String) = (1, "abc") // syntactic sugar
x: (Int, String) = (1,abc)
scala> val u: Unit = () // Like a tuple with 0 arguments !
u: Unit = ()

22. Types of functions
scala> val doubler: Function[Int, Int] = x => x * 2
doubler: Function[Int,Int] = <function1>
scala> val doubler: Int => Int = x => x * 2 // Alternative syntax
doubler: Int => Int = <function1>

23. Syntactic Sugar
scala> class @@[A, B]
scala> val test = new (Int @@ String)
test: @@[Int,String] = $at$at@6bddea9
scala> trait MyIntFn extends (Int => Int)

24. Variance
• Is List[Dog] a subtype of List[Animal] ? You decide!
class Covariant[+T]
class Contravariant[-T]
class Invariant[T]

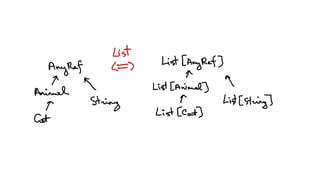
26. Variance
List[+T] // List[Dog] is a List[Animal]
Comparator[-B] // Comparator[Animal] can work as Comparator[Dog]
Function[-A, +R] // Think about it!
mutable.Set[A] // Can you say why ?
Covariant types can only appear in return positions
Contravariant types can only appear in argument positions
e.g. def apply(arg: A): R

27. Type Bounds
class CosmicList[A <: Cosmic]
class CosmicAnimalList[A <: Animal with Cosmic]
class ClosableList[A <: { def close: Unit }]
class ComparatorList[T >: Comparable]

28. Existential Types
scala> def length[T](list: List[T]): Int = list.length
length: [T](list: List[T])Int
scala> def length(list: List[T] forSome { type T }): Int = list.length
length: (list: List[_])Int
scala> def length(list: List[_]): Int = list.length // equivalent
length: (list: List[_])Int

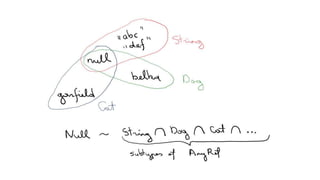
29. Existential types
Array[T] forSome { type T } // Array[_]
Array[T forSome { type T }] // Array[Any]
Map[Class[T forSome { type T }], String]
Map[Class[T] forSome { type T }, String] // Map[Class[_], String]
Map[Class[T], String] forSome { type T }

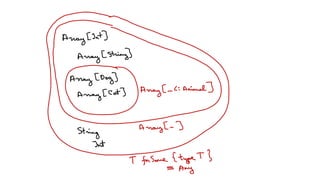
31. Type constructors
• List is a type constructor, i.e. given a type, it produces a type
• List is not a type! List[Int] is a type!

32. Higher Kinded Types
scala> class ContainerFactory[T, C[_]]
defined class ContainerFactory
scala> class ListFactory[T] extends ContainerFactory[T, List]
defined class ListFactory

33. Kinds of types
Int has kind * // analogous to value 1
List[Int] has kind * // analogous to value “abc”
List[_] has kind * // analogous to value ‘a’
List has kind * -> * // analogous to function x => x * x
ContainerFactory has kind (*, * -> *) -> * // analogous to (x, f) => f(x)

34. 1000000$ question
• What is a type equivalent to plus(2, _) ? i.e. x => plus(2, x)
• E.g. given Either[A, B] get a type constructor that produces types
Either[Int, T] given a type T

35. Naïve answer
• Either[Int, _] ?
scala> class EitherFactory[T] extends ContainerFactory[T, Either[Int, _]]
<console>:8: error: Either[Int, _] takes no type parameters, expected: one
class EitherFactory[T] extends ContainerFactory[T, Either[Int, _]]

36. Answer
class EitherFactory[T] extends ContainerFactory[T, ({ type λ[α] = Either[Int, α]})#λ]
defined class EitherFactory
Type lambdas !!
Future syntax: [α]=Either[Int, α]
Type members will be discussed next time

37. ({type λ[-α]= T[α] <~< T[A2]})#λ

38. References
• http://stackoverflow.com/a/3113741/919707 a list of scala types
• Wample & Payne, “Programming Scala”, chapter 12
• http://www.infoq.com/presentations/data-types-issues
• https://github.com/lampepfl/dotty EPFL’s attempt to optimize the system

39. Still to cover
• Type members
• Implicits
• Type classes
• Logic programming with types
• Type magic with Shapeless
• More examples