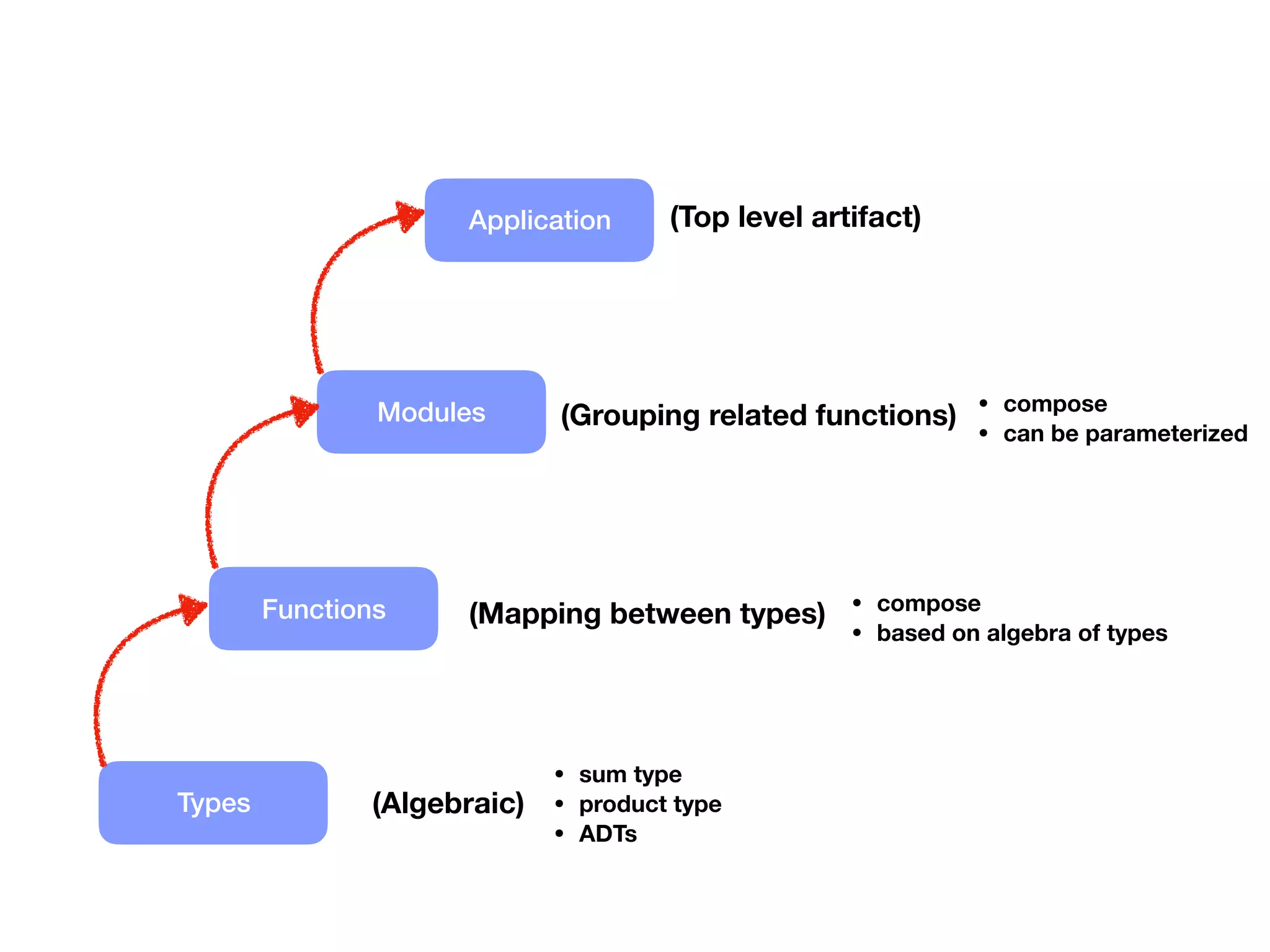
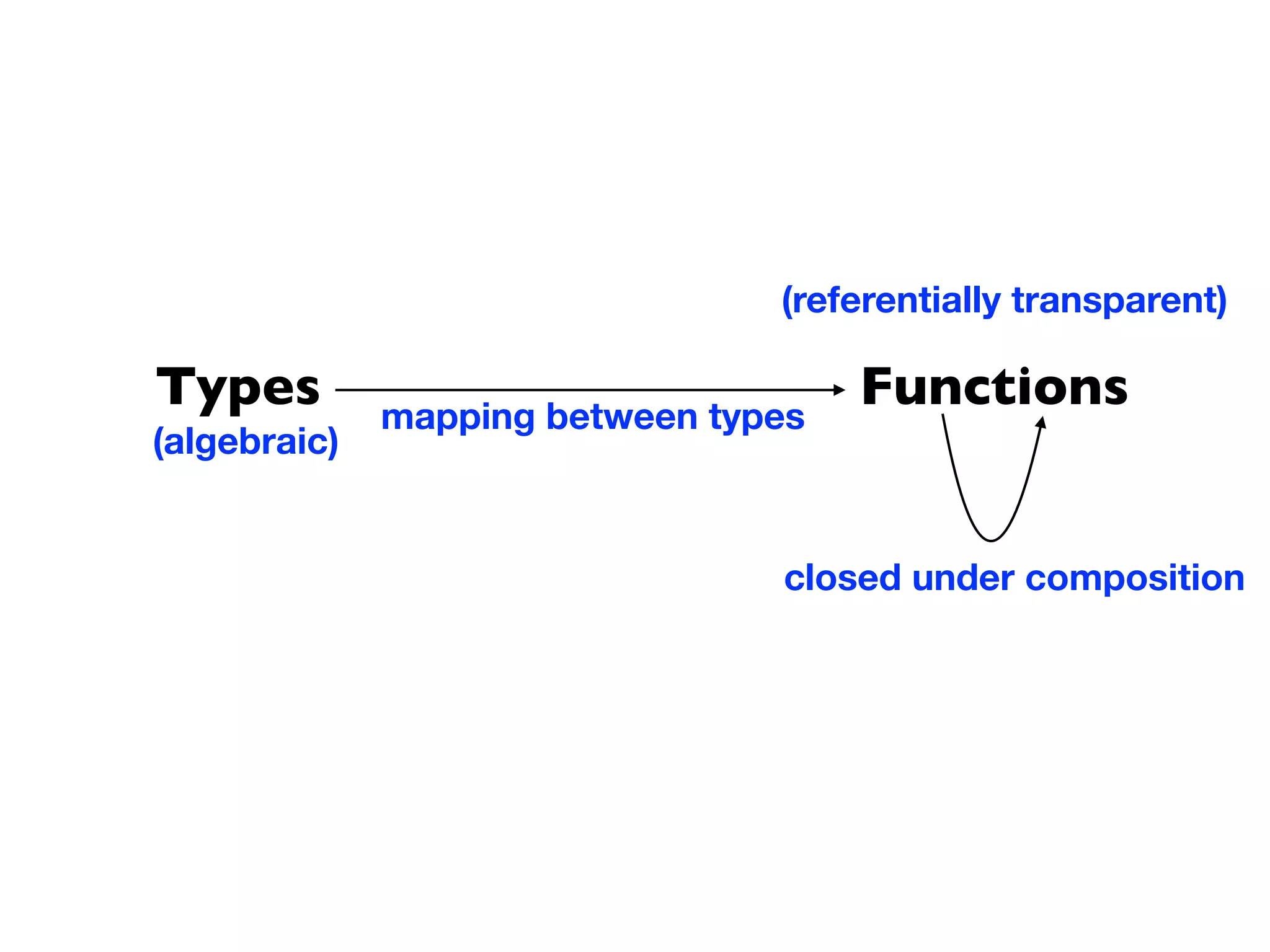
The document explores the concept of functions as the primary abstraction of design in a statically typed functional programming environment, emphasizing pure functions, referential transparency, and function composition. It discusses algebraic types, including product and sum types, and their role in creating modular and composable code structures. The document also examines practical examples in Scala, illustrating how these concepts enhance programming clarity and facilitate local reasoning.



: B](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-4-2048.jpg)




![def size(n: Int): Option[Int] =
if (n == 0) None else Some(1000 / n)
Pure Value](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-11-2048.jpg)





![scala> def foo(iter: Iterator[Int]) = iter.next + 2
foo: (iter: Iterator[Int])Int
scala> (1 to 20).iterator
res0: Iterator[Int] = non-empty iterator
scala> val a = foo(res0)
a: Int = 3
scala> (a, a)
res1: (Int, Int) = (3,3)
scala> (1 to 20).iterator
res3: Iterator[Int] = non-empty iterator
scala> (foo(res3), foo(res3))
res4: (Int, Int) = (3,4)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-17-2048.jpg)
![def foo(i: Iterator[Int]): Int = {
val a = i.next
val b = a + 1
a + b
}
scala> val i = (1 to 20).iterator
i: Iterator[Int] = non-empty iterator
scala> foo(i)
res8: Int = 3
scala> val i = (1 to 20).iterator
i: Iterator[Int] = non-empty iterator
scala> i.next + i.next + 1
res9: Int = 4
• non compositional
• hinders local understanding
• breaks RT](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-18-2048.jpg)









![Product Types in Scala
type Point = (Int, Int)
val p = (10, 12)
case class Account(no: String,
name: String,
address: String,
dateOfOpening: Date,
dateOfClosing: Option[Date]
)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-28-2048.jpg)





![sealed trait InstrumentType
case object CCY extends InstrumentType
case object EQ extends InstrumentType
case object FI extends InstrumentType
sealed trait Instrument {
def instrumentType: InstrumentType
}
case class Equity(isin: String, name: String, issueDate: Date,
faceValue: Amount) extends Instrument {
final val instrumentType = EQ
}
case class FixedIncome(isin: String, name: String, issueDate: Date,
maturityDate: Option[Date], nominal: Amount) extends Instrument {
final val instrumentType = FI
}
case class Currency(isin: String) extends Instrument {
final val instrumentType = CCY
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-34-2048.jpg)





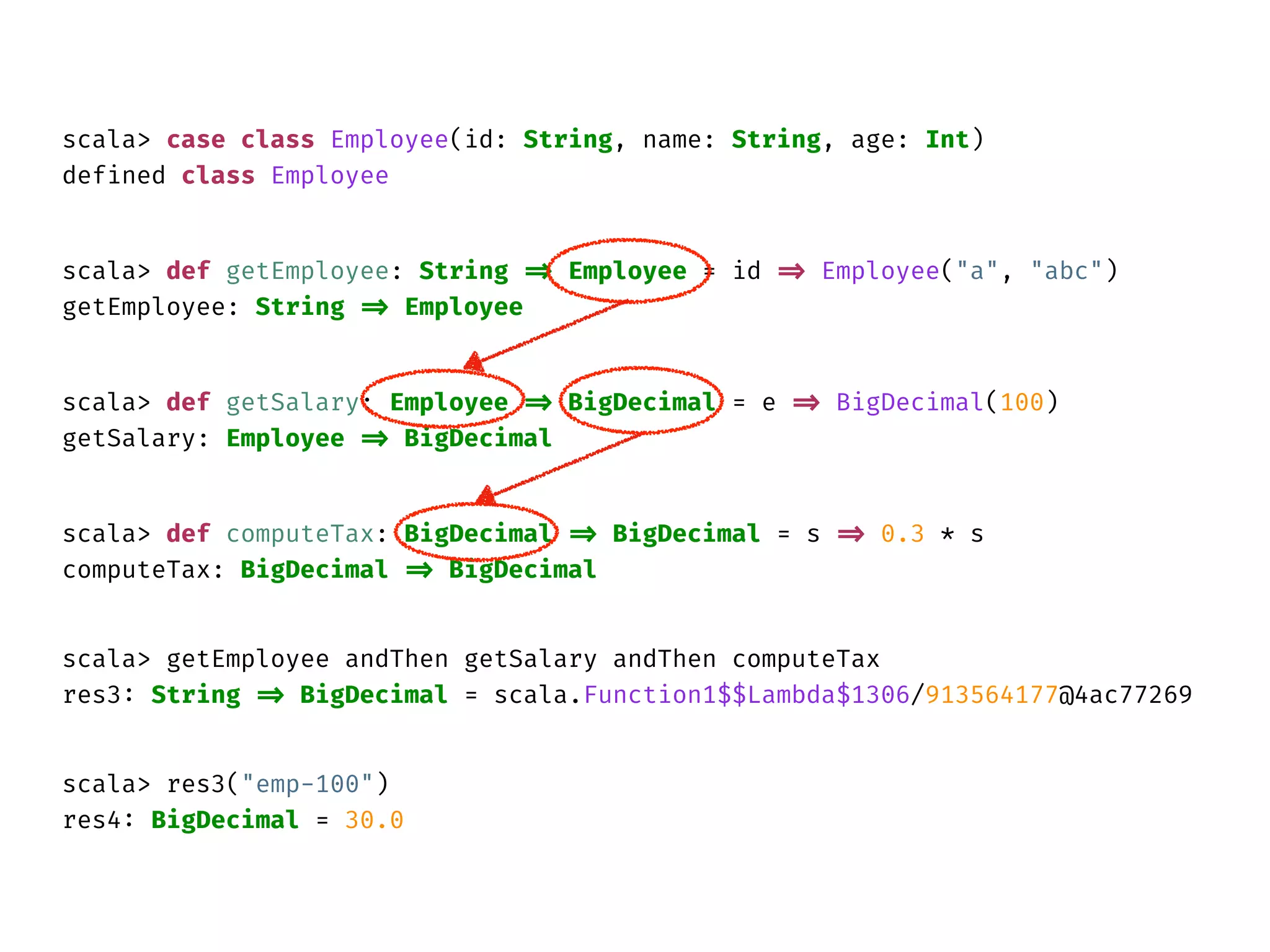

![Function Composition
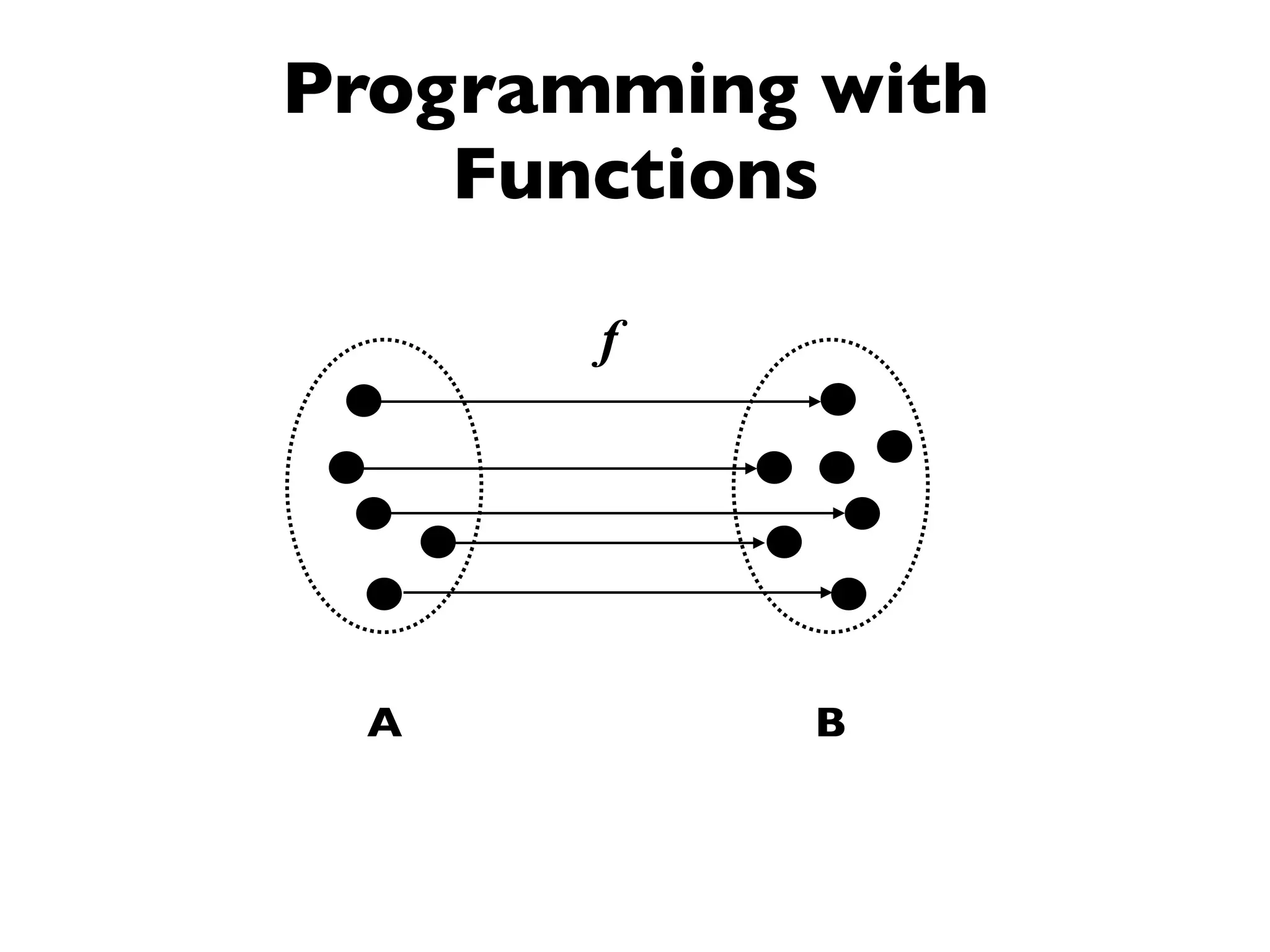
f:A => B
g:B => C
(f
andThen
g):A
=>
C
id[A]:A => A id[B]:B => B
(Slide adapted from a presentation by Rob Norris at Scale by the Bay 2017)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-42-2048.jpg)

![scala> List(1, 2, 3).map(e => e * 2)
res0: List[Int] = List(2, 4, 6)
scala> (1 to 10).filter(e => e % 2 == 0)
res2: s.c.i.IndexedSeq[Int] = Vector(2, 4, 6, 8, 10)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-44-2048.jpg)
![scala> def even(i: Int) = i % 2 == 0
even: (i: Int)Boolean
scala> (1 to 10).filter(even)
res3: s.c.i.IndexedSeq[Int] = Vector(2, 4, 6, 8, 10)
scala> (1 to 10).foldLeft(0)((a, e) => a + e)
res4: Int = 55](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-45-2048.jpg)

![def size(n: Int): Option[Int] =
if (n == 0) None else Some(1000 / n)
Pure Value](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-47-2048.jpg)
![def size(n: Int): Either[String,Int] =
if (n == 0) Left(“Division by zero”)
else Right(1000 / n)
Pure Value](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-48-2048.jpg)
![def size(n: Int): Either[String,Int] =
if (n == 0) Left(“Division by zero”)
else Right(1000 / n)
Sum Type
Error Path
Happy Path](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-49-2048.jpg)


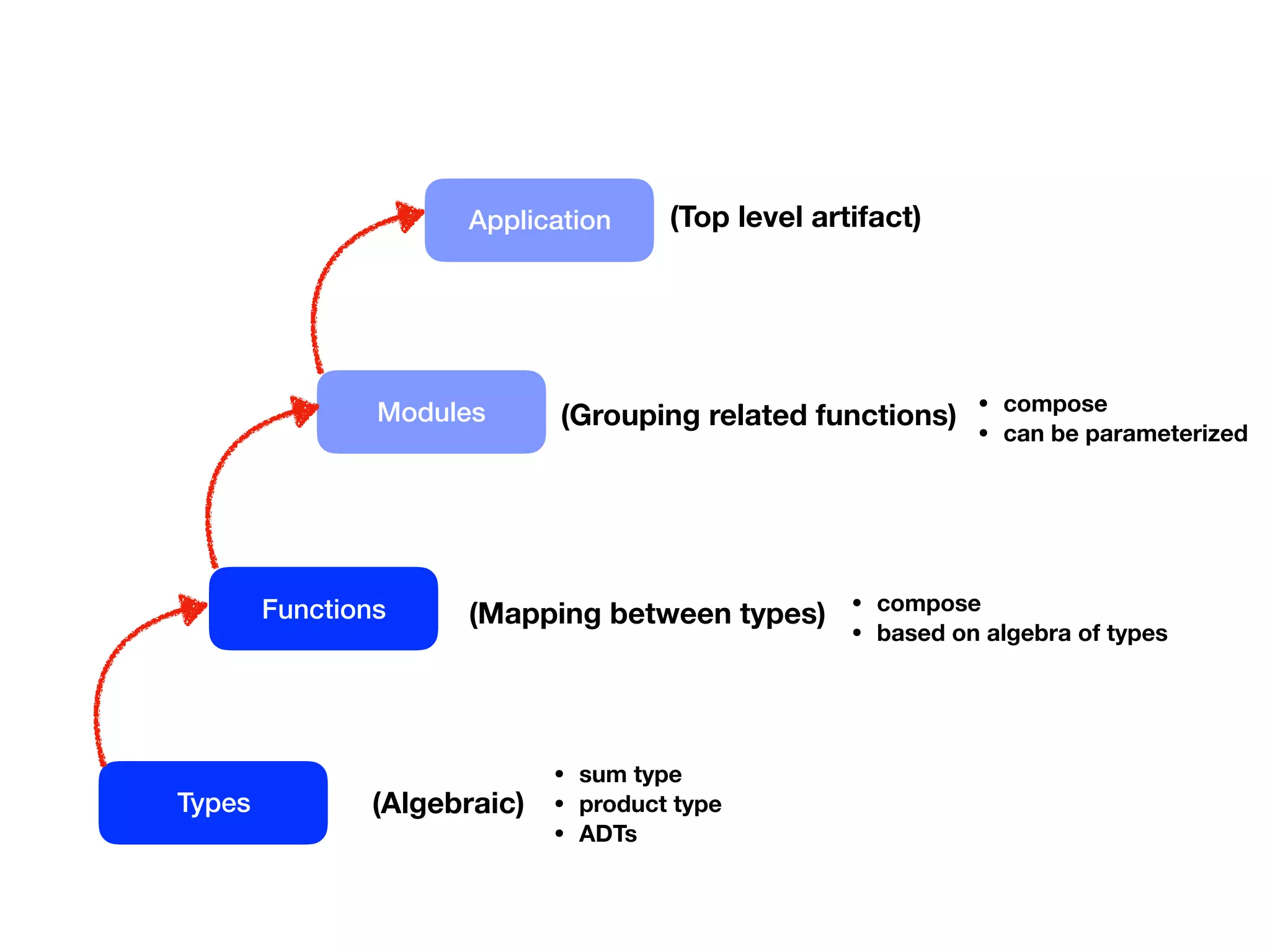
![trait Combiner[A] {
def zero: A
def combine(l: A, r: => A): A
}
//identity
combine(x, zero) =
combine(zero, x) = x
// associativity
combine(x, combine(y, z)) =
combine(combine(x, y), z)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-54-2048.jpg)
![Module with an algebra
trait Monoid[A] {
def zero: A
def combine(l: A, r: => A): A
}
//identity
combine(x, zero) =
combine(zero, x) = x
// associativity
combine(x, combine(y, z)) =
combine(combine(x, y), z)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-55-2048.jpg)
![Module with an Algebra
trait Foldable[F[_]] {
def foldl[A, B](as: F[A], z: B, f: (B, A) => B): B
def foldMap[A, B](as: F[A], f: A => B)
(implicit m: Monoid[B]): B =
foldl(as,
m.zero,
(b: B, a: A) => m.combine(b, f(a))
)
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-56-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
https://stackoverflow.com/a/4765918](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-57-2048.jpg)
![case class Sum(value: Int)
case class Product(value: Int)
implicit val sumMonoid = new Monoid[Sum] {
def zero = Sum(0)
def add(a: Sum, b: Sum) = Sum(a.value + b.value)
}
implicit val productMonoid = new Monoid[Product] {
def zero = Product(1)
def add(a: Product, b: Product) =
Product(a.value * b.value)
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-58-2048.jpg)

![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-60-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
combinator
(higher order function)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-61-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
Type constructor](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-62-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
F needs to honor the
algebra of a Foldable](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-63-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
B needs to honor the
algebra of a Monoid](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-64-2048.jpg)
![def mapReduce[F[_], A, B](as: F[A], f: A => B)
(implicit ff: Foldable[F], m: Monoid[B]) =
ff.foldMap(as, f)
combinator
(higher order function)
Type constructor
F needs to honor the
algebra of a Foldable
B needs to honor the
algebra of a Monoid](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-65-2048.jpg)
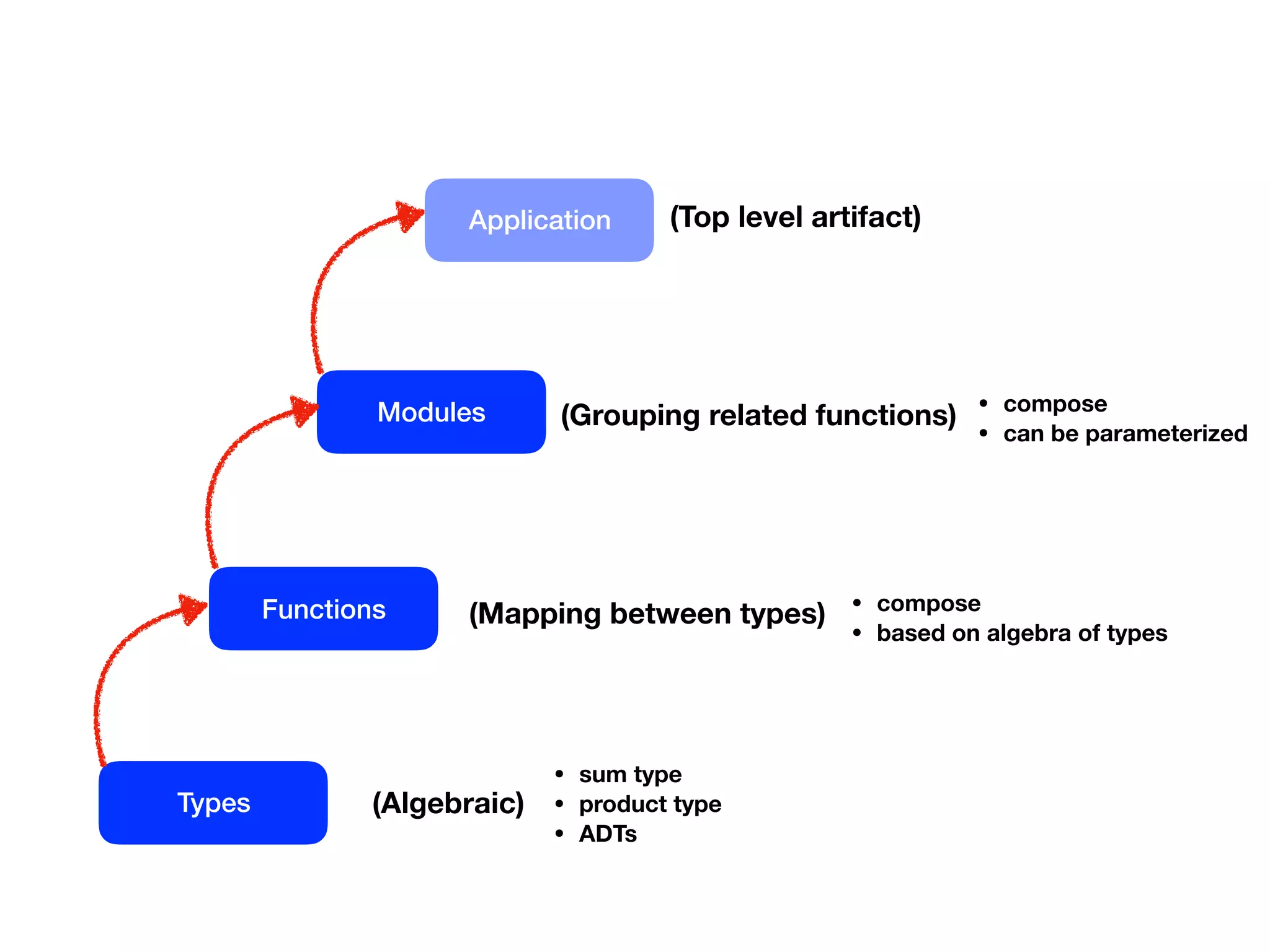

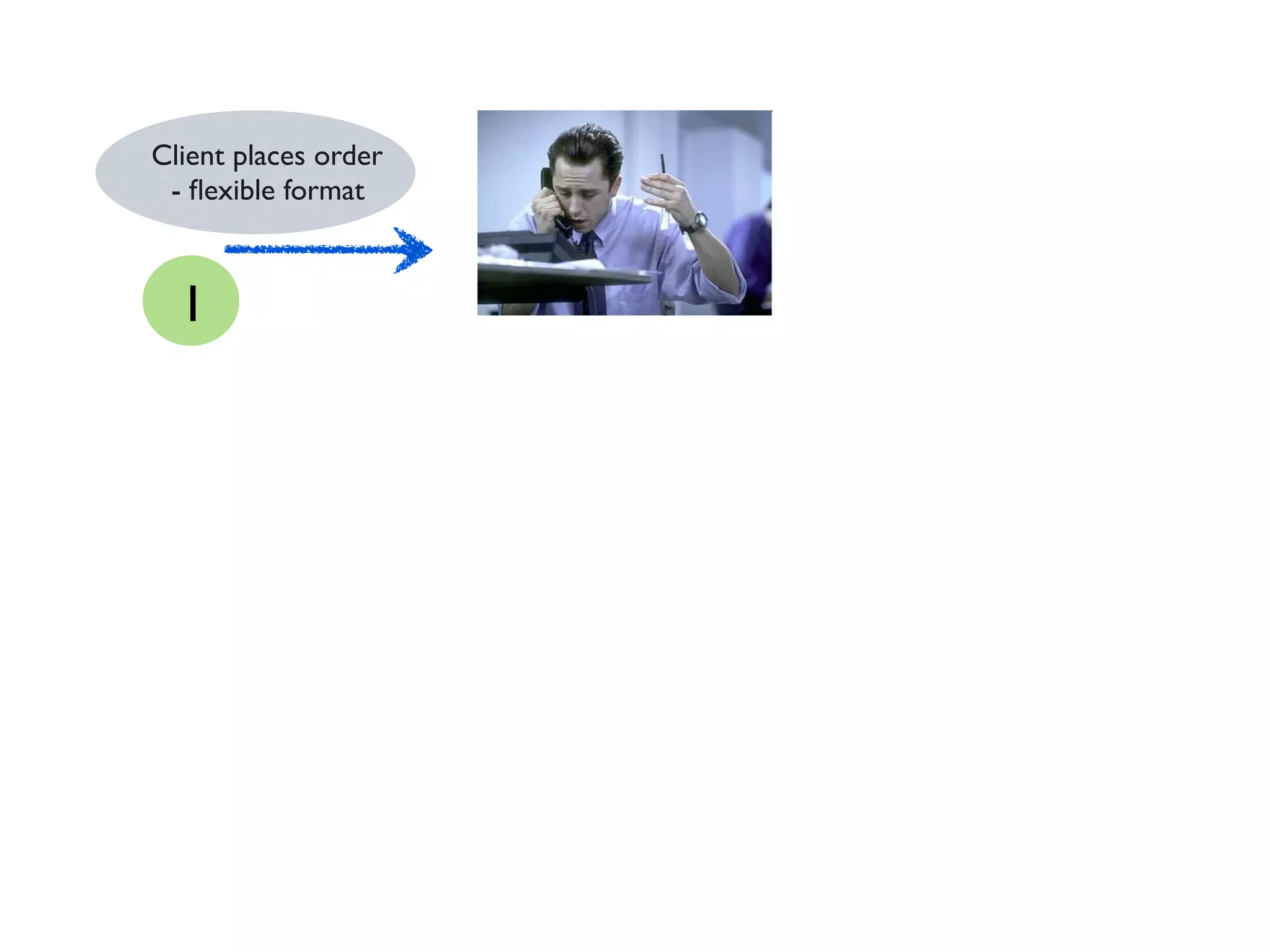
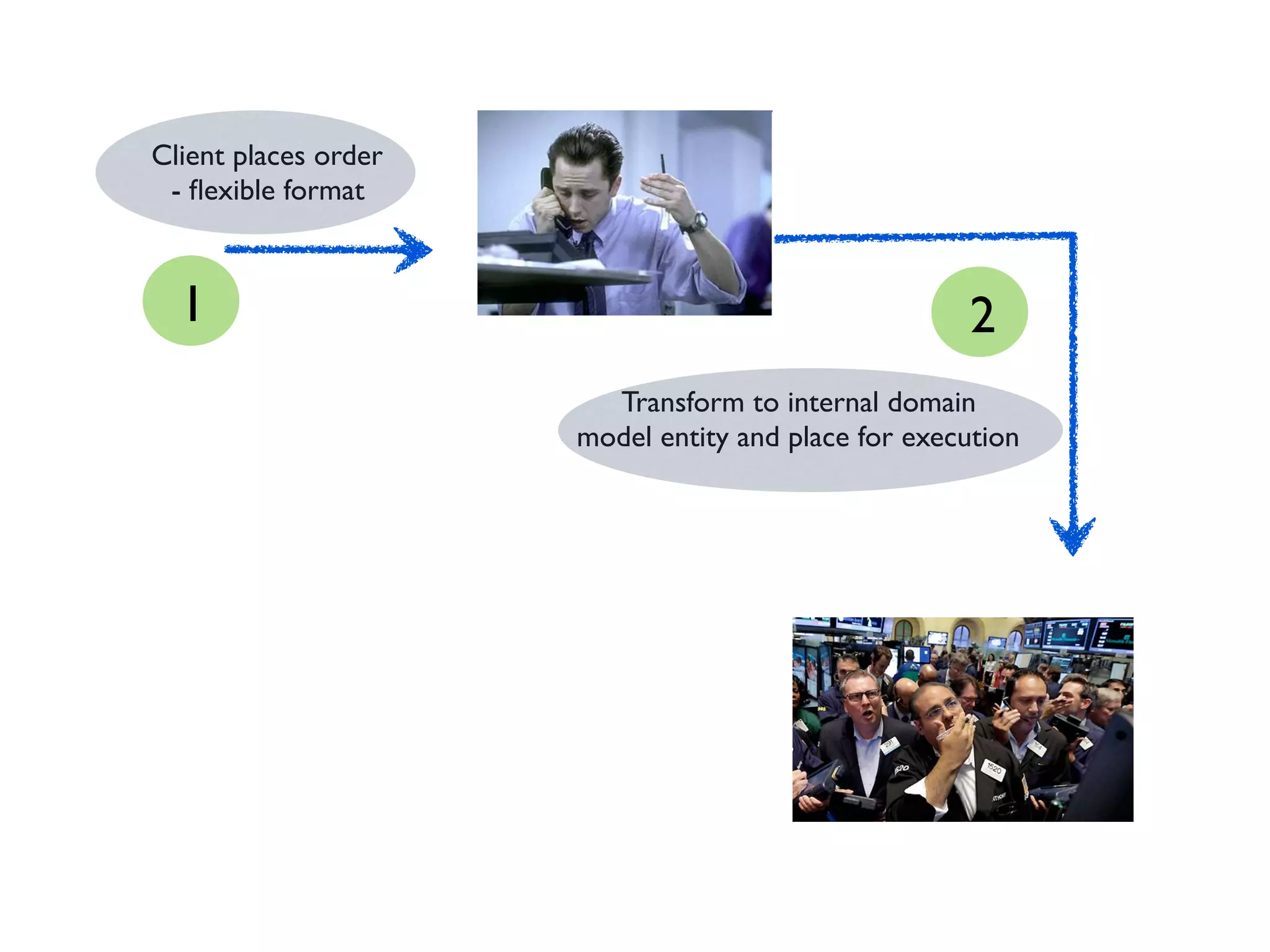
![def clientOrders:
List[ClientOrder] => List[Order]](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-71-2048.jpg)
![def clientOrders:
List[ClientOrder] => Either[Error,
List[Order]]](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-72-2048.jpg)
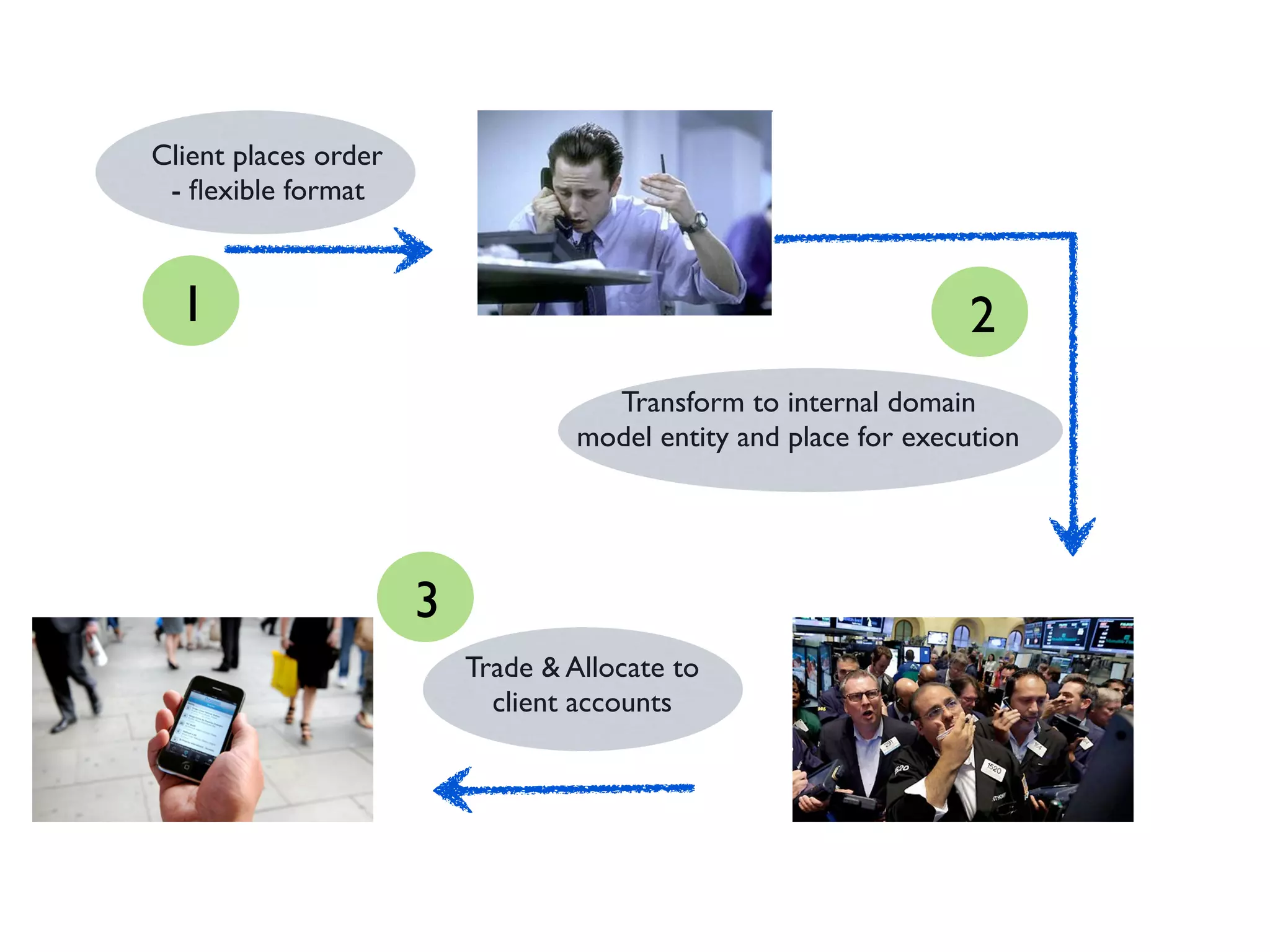
![def clientOrders:
List[ClientOrder] => Either[Error, List[Order]]
def execute(market: Market, brokerAccount: Account):
List[Order] => Either[Error, List[Execution]]
def allocate(accounts: List[Account]):
List[Execution] => Either[Error, List[Trade]]](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-73-2048.jpg)
![Function Composition
f:A => B
g:B => C
(f
andThen
g):A
=>
C
id[A]:A => A id[B]:B => B
(Slide adapted from a presentation by Rob Norris at Scale by the Bay 2017)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-74-2048.jpg)
![def clientOrders:
List[ClientOrder] => Either[Error, List[Order]]
def execute(market: Market, brokerAccount: Account):
List[Order] => Either[Error, List[Execution]]
def allocate(accounts: List[Account]):
List[Execution] => Either[Error, List[Trade]]](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-75-2048.jpg)

![We have those pesky Either[Error, ..]
floating around](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-77-2048.jpg)


![Effectful Function
Composition
f:A => F[B]
g:B => F[C]
(f
andThen
g):A
=>
F[C]
pure[A]:A => F[A] pure[B]:B => F[B]
(Slide adapted from a presentation by Rob Norris at Scale by the Bay 2017)](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-80-2048.jpg)
![Effectful Function
Composition
final case class Kleisli[F[_], A, B](run: A => F[B]) {
def andThen[C](f: B => F[C])
: Kleisli[F, A, C] = // ..
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-81-2048.jpg)
![type ErrorOr[A] = Either[Error, A]
def clientOrders:
Kleisli[ErrorOr, List[ClientOrder], List[ClientOrder]]
def execute(market: Market, brokerAccount: Account):
Kleisli[ErrorOr, List[Order], List[Execution]]
def allocate(accounts: List[Account]):
Kleisli[ErrorOr, List[Execution], List[Trade]]](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-82-2048.jpg)
![def tradeGeneration(
market: Market,
broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-83-2048.jpg)
![type ErrorOr[A] = Either[Error, A]
def clientOrders:
Kleisli[ErrorOr, List[ClientOrder], List[ClientOrder]]
def execute(market: Market, brokerAccount: Account):
Kleisli[ErrorOr, List[Order], List[Execution]]
def allocate(accounts: List[Account]):
Kleisli[ErrorOr, List[Execution], List[Trade]]
def tradeGeneration(market: Market, broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-84-2048.jpg)
![type ErrorOr[A] = Either[Error, A]
def clientOrders:
Kleisli[ErrorOr, List[ClientOrder], List[ClientOrder]]
def execute(market: Market, brokerAccount: Account):
Kleisli[ErrorOr, List[Order], List[Execution]]
def allocate(accounts: List[Account]):
Kleisli[ErrorOr, List[Execution], List[Trade]]
def tradeGeneration(market: Market, broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}
trait TradingService {
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-85-2048.jpg)
![type ErrorOr[A] = Either[Error, A]
def clientOrders:
Kleisli[ErrorOr, List[ClientOrder], List[ClientOrder]]
def execute(market: Market, brokerAccount: Account):
Kleisli[ErrorOr, List[Order], List[Execution]]
def allocate(accounts: List[Account]):
Kleisli[ErrorOr, List[Execution], List[Trade]]
def tradeGeneration(market: Market, broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}
trait TradingService {
}](https://image.slidesharecdn.com/typed-functions-jvm-181213155417/75/Power-of-functions-in-a-typed-world-86-2048.jpg)

