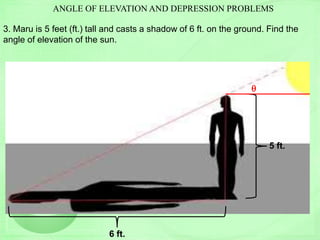
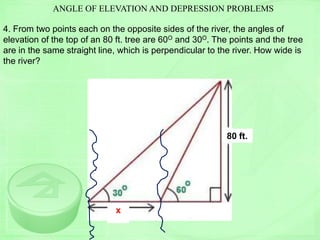
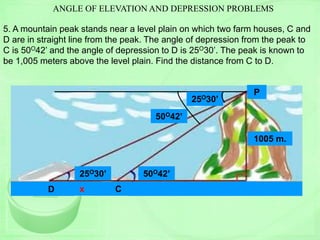
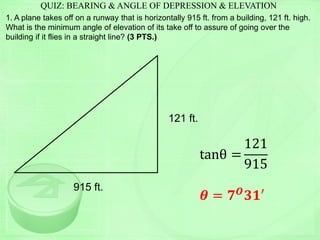
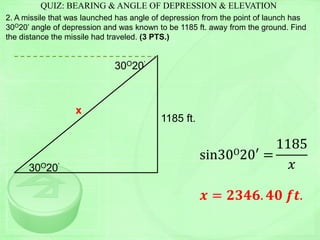
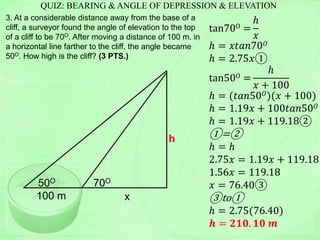
The document provides a trigonometry diagnostic exam with 4 problems: 1) Find trig functions if sinθ = 3/5 2) Find trig functions if secM = 6/5 3) Find 6 trig functions of angle P 4) Solve a trig expression given sin, tan, cos values The problems require finding trig functions based on a given value, expressing answers in simplest form. Students have 10 minutes to complete the problems.

1. TRIGONOMETRY

2. 1. Find other functions of  if its 𝑠𝑖𝑛𝜃 =
3
5
. (5 PTS.)
2. 𝑠𝑒𝑐𝑀 =
6
5
, find the other trigonometric functions. (5 PTS.)
3. Find the 6 trigonometric functions considering P. (6 PTS.)
4. Given that 𝑠𝑖𝑛𝐷 =
4
5
, ta𝑛𝐸 =
5
12
, 𝑎𝑛𝑑 𝑐𝑜𝑠𝐹 =
8
17
solve for
𝑐𝑠𝑐𝐷 2 ∙ 𝑐𝑜𝑡𝐹 ∙ 𝑐𝑜𝑡𝐸 (4 PTS.)
Solve what is asked. Express your answers in simplest form.
Good for 10 minutes.
End

3. 1. Find other functions of  if its 𝑠𝑖𝑛𝜃 =
3
5
𝑠𝑖𝑛𝜃 =
3
5
𝑐𝑠𝑐𝜃 =
5
3
𝑐𝑜𝑠𝜃 =
4
5
𝑠𝑒𝑐𝜃 =
5
4
𝑡𝑎𝑛𝜃 =
3
4
𝑐𝑜𝑡𝜃 =
4
3
2. 𝑠𝑒𝑐𝑀 =
6
5
, find the other trig. functions.
𝑠𝑒𝑐𝑀 =
6
5
𝑡𝑎𝑛𝑀 =
11
5
𝑠𝑖𝑛𝑀 =
11
6
𝑐𝑠𝑐𝑀 =
6 11
11
𝑐𝑜𝑠𝑀 =
5
6
𝑐𝑜𝑡𝑀 =
5 11
11
3. Find the 6 trigonometric functions considering P
𝑠𝑖𝑛𝑃 =
76
20
𝑐𝑠𝑐𝑃 =
20 76
76
=
5 76
19
𝑐𝑜𝑠𝑃 =
18
20
=
9
10
𝑠𝑒𝑐𝑃 =
20
18
=
10
9
𝑡𝑎𝑛𝑀 =
76
18
𝑐𝑜𝑡𝑃 =
18 76
76
=
9 76
38
4. Given that 𝑠𝑖𝑛𝐷 =
4
5
, ta𝑛𝐸 =
5
12
, 𝑎𝑛𝑑 𝑐𝑜𝑠𝐹 =
8
17
solve for 𝑐𝑠𝑐𝐷 2
∙ 𝑐𝑜𝑡𝐹 ∙ 𝑐𝑜𝑡𝐸
𝑐𝑠𝑐𝐷 2
∙ 𝑐𝑜𝑡𝐹 ∙ 𝑐𝑜𝑡𝐸 =
25
16
∙
12
5
∙
8
15
= 2

4. DAY 1
 DIAGNOSTIC EXAM (TRIGONOMETRY)
 SIX TRIGONOMETRIC FUNCTIONS
 SOHCAHTOA
 PYTHAGOREAN TRIPLE

5. DAY 2
 REVIEW QUIZ
 UNIT CIRCLE
 SPECIAL ANGLES
 SIGN CHART OF FUNCTION ANGLES
 REFERENCE ANGLE

7. DAY 2
 REVIEW QUIZ
 UNIT CIRCLE
 6 TRIG. FNCS OF SPECIAL ANGLES (30O, 45O, 60O)
 SIGN CHART OF FUNCTION ANGLES (Ang Sarap
Tumitig ni Crush)
 STANDARD POSITION
 REFERENCE ANGLE
 KINDS OF ANGLES (addt’l: perigon/round, conjugate
angles, coterminal angles)
 CONVERSION
 Degree to radians
 Radians to degrees
 REVOLUTION SYSTEM
 SEXAGESIMAL SYTEM
 Operation on DMS (degree, minute & second notation)
RECAP

8. DAY 3
 REVIEW QUIZ
 CIRCULAR SYSTEM
 WRAPPING FUNCTIONS
 QUADRANTAL ANGLES
 TRIGONOMETRIC FUNCTIONS OF NEGATIVE
ANGLES
 GRAPHS OF TRIGONOMETRIC FUNCTIONS
 BEARING

9. REVIEW QUIZ 2: SET A
1. Determine a.) reference angle b.) 6 trigo. fnc. of 𝜃 = 495 𝑂
2. Evaluate the following: a.) cot 330 𝑂 𝑏. ) 𝑐𝑜𝑠
5𝜋
4
𝑐. )𝑡𝑎𝑛
7𝜋
6
𝑑. ) 𝑠𝑖𝑛 −
3𝜋
4
3. Determine sin A and sec A if 𝑡𝑎𝑛𝐴 =
8
6
. Express your answers in
simplest form.
4. Given that 𝑠𝑖𝑛𝐷 =
4
5
, 𝑡𝑎𝑛𝐸 =
5
12
, 𝑎𝑛𝑑 𝑐𝑜𝑡𝐺 =
24
7
. Solve for the value of
𝑐𝑜𝑠𝐷 2 ∙ 𝑠𝑒𝑐𝐺 ∙ 𝑐𝑜𝑠𝐸
5. Given: 𝑡𝑎𝑛𝜃 = 3, 𝜃 𝑖𝑛 𝑄𝐼𝐼𝐼. Find the other trigonometric functions.
6. Convert to degrees / radians: a.) 75O b.) 270O c.) 11/6 d.) -4/5
7. ALTERNATIVE RESPONSE: Write TRUE or FALSE. Any form of
erasure means wrong.
a.) An equiangular triangle is also equilateral.
b.) Secant  is the reciprocal of sine .
c.) The sum of all angles of any triangle is 360.
d.) An angle is positive if the direction is counterclockwise.
e.) 285 and 75 are coterminal angles.

10. REVIEW QUIZ 2: SET B
1. Determine a.) reference angle b.) 6 trigo. fnc. of 𝜃 = −240 𝑂
2. Evaluate the following:
a.) sin 135 𝑂 𝑏. ) 𝑐𝑜𝑠 − 330 𝑂 𝑐. )𝑡𝑎𝑛
3𝜋
4
𝑑. ) 𝑠𝑖𝑛 −45 𝑂 tan −120𝑂 cos(
5𝜋
6
)
3. Determine a.)csc A b.) sec A if co𝑡𝐴 =
9
12
. Express your answers in
simplest form.
4. Given that 𝑠𝑖𝑛𝐷 =
4
5
, 𝑡𝑎𝑛𝐸 =
5
12
, 𝑎𝑛𝑑 𝑐𝑜𝑠𝐹 =
8
17
. Solve for the value of
𝑐𝑠𝑐𝐷 2 ∙ 𝑐𝑜𝑡𝐹 ∙ 𝑐𝑜𝑡𝐸
5. Given: 𝑡𝑎𝑛𝜃 = −
3
3
, 𝜃 𝑖𝑛 𝑄𝐼𝑉. Find the other trigonometric functions.
6. Convert to degrees / radians: a.) -210O b.) 240O c.) -7/4 d.) 7/6
7. ALTERNATIVE RESPONSE: Write TRUE or FALSE. Any form of
erasure means wrong.
a.) In a right triangle having acute angles of 30O and 60O, the length of the
side opposite 30O is one-half the length of the adjacent side.
b.) If the value of one function of an acute angle is known, it is possible to
find the other five functions.
c.) Pythagorean theorem can be applied in any kind of triangle.
d.) The reciprocal function of secant is sine.
e.) The shorter leg of 30O-60O-90O triangle is 1.

11. ANSWERS: REVIEW QUIZ 2 SET B
1. 𝜃 = −240 𝑂
a.) 60
b.) 𝑠𝑖𝑛 −240 𝑂 =
3
2
cs𝑠 −240 𝑂 =
2 3
3
𝑐𝑜𝑠 −240 𝑂 = −
1
2
𝑠𝑒𝑐 −240 𝑂 = −2
𝑡𝑎𝑛 −240 𝑂 = − 3 cot −240 𝑂 = −
3
3
2. a.) 𝑠𝑖𝑛135 𝑂
=
2
2
b.) 𝐶𝑂𝑆 − 330 𝑂 =
3
2
c.) 𝑡𝑎𝑛
3𝜋
4
= −1
d.) 𝑠𝑖𝑛 −45 𝑂 𝑡𝑎𝑛 −120𝑂 𝑐𝑜𝑠
5𝜋
6
= −
2
2
3
1
−
3
2
=
3 2
4
3. 𝑐𝑠𝑐𝐴 =
5
4
b.) 𝑠𝑒𝑐𝐴 =
5
3
4. 𝑐𝑠𝑐𝐷 2 =
25
16
𝑐𝑜𝑡𝐹 =
8
15
cot 𝐸 =
12
5
= 2
5. a.)sin 𝜃 = −
1
2
b.) cos 𝜃 =
3
2
c.) ccs 𝜃 = −2 d.) sec 𝜃 =
2 3
3
e.) cot 𝜃 = − 3
6. a.) −210 𝑂 = −
7𝜋
6
𝑟𝑎𝑑. b.) 240O=
4𝜋
3
𝑟𝑎𝑑. c.)-315O d.) 210O
7. a.) FALSE b.) TRUE c.) FALSE d.) FALSE e.) TRUE

12. Circular system – radian(rad) is the fundamental unit
- one radian is the measure of an angle, which if its vertex is
placed at the center of a circle, subtends an arc equal to the radius of the circle
From Geometry:
c = 2r, if r = 1 rad
then c = 2radians, we know that c = 360O
Hence
2𝜋𝑟𝑎𝑑𝑖𝑎𝑛𝑠
2
=
360
2
radians = 180O
1 𝑟𝑎𝑑 =
180 𝑂
𝜋
1 𝑂
=
𝜋𝑟𝑎𝑑
180 𝑂
𝜃 =
𝑎𝑟𝑐𝑙𝑒𝑛𝑔𝑡ℎ
𝑟𝑎𝑑𝑖𝑢𝑠
=
𝑠
𝑟
s= 𝜃r
From radian to degree
From degree to radian

13. WRAPPING FUNCTIONS

15. 30O
1
2
3
𝝅
𝟔
= 𝟑𝟎 𝑶

16. 𝝅
𝟒
= 𝟒𝟓 𝑶

17. 𝝅
𝟔
= 𝟔𝟎 𝑶

18. 𝑺𝑼𝑴𝑴𝑨𝑹𝒀

19. 𝑬𝑿𝑬𝑹𝑪𝑰𝑺𝑬
Find the coordinates of the circular points.
1. 𝑤 −
𝜋
2
2. 𝑤
8𝜋
6
3. 𝑤 −𝜋
4. 𝑤
3𝜋
4
5. 𝑤 2𝜋

20. 𝑬𝑿𝑬𝑹𝑪𝑰𝑺𝑬: 𝑺𝑬𝑻 𝑩
Find the coordinates of the circular points.
1. 𝑤
5𝜋
6
2. 𝑤 −3𝜋
3. 𝑤
11𝜋
4
4. 𝑤 −
4𝜋
3
5. 𝑤 6𝜋

21. 𝑨𝑵𝑺𝑾𝑬𝑹𝑺: 𝑺𝑬𝑻 𝑩
Find the coordinates of the circular points.
1. 𝑤
5𝜋
6
= −
3
2
,
1
2
2. 𝑤 −3𝜋 = −1,0
3. 𝑤
11𝜋
4
= −
2
2
,
2
2
4. 𝑤 −
4𝜋
3
= −
1
2
, −
3
2
5. 𝑤 6𝜋 = 1,0

22. QUADRANTAL ANGLES
QUADRANTAL ANGLE – terminal side of an angle in standard position coincides with one of
the coordinate axes: 0O
/360O
, 90O
, 180O
, 270O
1,0
𝑥 = 1
𝑦 = 0
𝑟 = 1
𝑠𝑖𝑛0 𝑂 =
𝑦
𝑟
=
0
1
= 0
𝑐𝑜𝑠0 𝑂
=
𝑥
𝑟
=
1
1
= 1
𝑡𝑎𝑛0 𝑂
=
𝑦
𝑥
=
0
1
= 0
𝑐𝑠𝑐0 𝑂
=
𝑟
𝑦
=
1
0
= ∞
𝑠𝑒𝑐0 𝑂 =
𝑟
𝑥
=
1
1
= 1
𝑡𝑎𝑛0 𝑂 =
𝑥
𝑦
=
1
0
= ∞

23.  sin
y
r
  cos
x
r
  tan
y
x
  csc
r
y
  sec
r
x
  cot
x
y
 
0O
,360O 0
0
1

1
1
1

0
0
1

1
0
 
1
1
1

1
0
 
90O 1
1
1

0
0
1

1
0
 
1
1
1

1
0
 
0
0
1

180O 0
0
1

1
1
1

 
0
0
1


1
0
 
1
1
1
 

1
0

 
270O 1
1
1

 
0
0
1

1
0

 
1
1
1
 

1
0
 
0
0
1


𝑺𝑼𝑴𝑴𝑨𝑹𝒀
Example: Evaluate
= 450O + 540O + 630O + 720O
= 90O + 180O + 270O + 360O
= 0 + (-1) + 0 +1
= 0

24. TRIGONOMETRIC FUNCTIONS OF NEGATIVE ANGLESTRIGONOMETRIC FUNCTIONS OF NEGATIVE ANGLES
sin (- ) =
y
r

=-sin csc (- ) =
r
y
= -csc
cos (- ) =
x
r
= cos sec (- ) =
r
x
= sec
tan (- ) =
y
x

= -tan cot (- ) =
x
y
= -cot
Examples: Evaluate the following:
1. tan (-45O
) 2. cos (-60O
) 3. csc (-450O
)
-
r -y
x
P (x, y)
= −𝑡𝑎𝑛45 𝑂
= −
1
1
= -1
= 𝑐𝑜𝑠60 𝑂
=
1
2
= −𝑐𝑠𝑐450 𝑂
= −𝑐𝑠𝑐90 𝑂
= −1

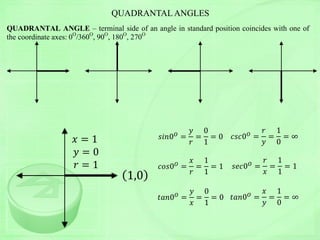
25. GRAPHS OF TRIGONOMETRIC FUNCTIONSGRAPHS OF TRIGONOMETRIC FUNCTIONS
A. Sine function
B. Cosine function Cosine function
0
0.25
0.5
0.75
1
sinevalue
Pro
P
A
D
R
N
Pro
P
A
D
R
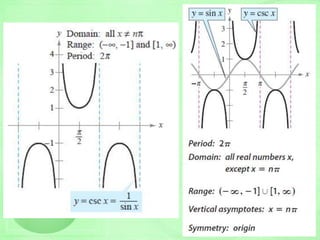
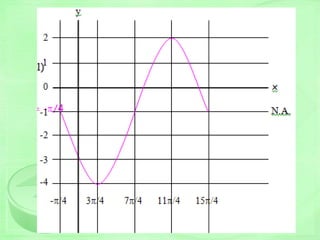
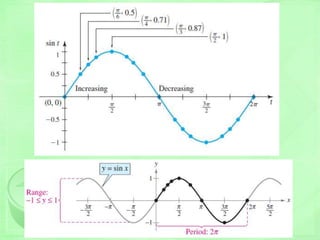
y = sin x
Properties:
Period = 2
Amplitude = 1
Domain = 
Range = [-1, 1]
Nature: symmetric
with respect to
the origin

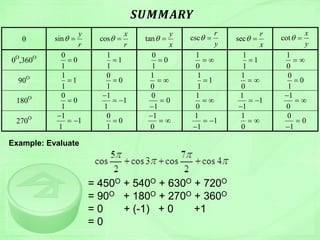
27. B. Cosine function Cosine function
-1
-0.75
-0.5
-0.25
0
0.25
0.5
0.75
1
0 30 60 90 120 150 180 210 240 270 300 330 360
degrees
cosinevalue
Pry = sin x
Properties:
Period = 2
Amplitude = 1
Domain = 
Range = [-1, 1]
Nature: symmetric
with respect to
the origin
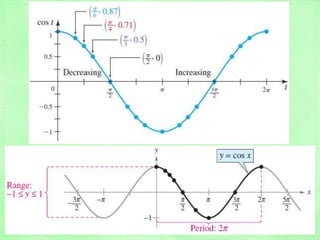
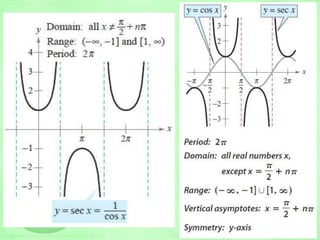
y = cos x
Properties:
Period = 2
Amplitude = 1
Domain = 
Range = [-1, 1]
Nature: symmetric
with respect to
the y-axis

29. Tangent function
-2.75
-2
-1.25
-0.5
0.25
1
1.75
2.5
-90 -60 -30 0 30 60 90 120 150 180
degrees
tangentvalue
y = tan x
Properties:
Period = 
Amplitude = undefined
Domain =  2
k    , k is an integer
Range = 
Nature: symmetric with respect to the
origin
Increasing function between consecutive
asymptotes
Discontinuous at 2
x k   , k is an
integer

34. PARTS OF THE GRAPH
DEFINITION OF TERMS
1. Nodes – points where the curve intersects the neutral axis
2. Amplitude – absolute value of the maximum distance of the curve from the neutral axis
3. Period – duration (in degrees/radians) to complete a cycle
4. Wavelength – complete cycle
nodes
period
wavelength
N.A. (neutral axis)
amplitude

35. PROPERTIES OF GRAPHS OF TRIGONOMETRIC FUNCTION
Different Graphs Properties
1.
sin
cos
y a x
y a x
 
 
Amplitude
Period
a
2
2.
sin
cos
y a bx
y a bx
 
 
Amplitude
Period
a
2
b

(the effect of b is it stretches or compresses
the graph so that its new period is 2/b)
3.
 
 
sin
cos
y a bx c
y a bx c
    
    
Amplitude
Period
Phase shift
End point
a
2
b

c
b
(if
c
b
is positive, curve shifts to the right)
(if
c
b
is negative, curve shifts to the left)
c
b
+
2
b

(starting point + period
4.
 
 
sin
cos
y a bx c d
y a bx c d
     
     
Amplitude
Period
Phase shift
Translation
a
2
b

c
b
d (if d is positive, N.A. shift above the x-axis)
(if d is negative, N.A. shift below the x-axis)

36. PRACTICE
𝒚 = −𝟑𝒔𝒊𝒏
𝟏
𝟐
𝒙 +
𝝅
𝟖
− 𝟏
Amplitude = −3 = 3
Period =
2𝜋
𝑏
=
2𝜋
1
2
=
2𝜋
1
∙
2
1
= 4𝜋
Interval =
4𝜋
4
= 𝜋
Phase shift =
𝑐
𝑏
=
−
𝜋
8
1
2
= −
𝜋
2
∙
2
1
= −
𝜋
4
End point = 𝑝ℎ𝑎𝑠𝑒 𝑠ℎ𝑖𝑓𝑡 + 𝑝𝑒𝑟𝑖𝑜𝑑 = −
𝜋
4
+ 4𝜋=
15𝜋
4
Translation = -1

38. x
180o
150o
120o
90o
60o
30o
Refer to the graph below
_____ 1 . The figure describes the graph of
A. cosine function B. cosecant function C. tangent function D. cotangent function
_____ 2. The number of cycles the graph has
A. 2 B. 3 C. 4 D. 5
_____ 3. The equation of the graph is
A. y = tan3x B. y = cos3x C. y = sin3x D. y = cot3x
_____ 4. What is the period of the function?
A. 30o
B. 60o
C. 90o
D. 120o
_____ 5. The function has a frequency of
A. 2 B. 3 C. 4 D. 5
_____ 6. The range of the function is equal to
A. -∞ ≤ y ≥ +∞ B. 0 ≤ y ≤ +∞ C. 0 ≤ y ≤ -∞ D. y ≥ +∞
_____ 7. Which of the following does not belong to the group?
A. 30o
B. 90o
C. 120o
D. 150o
_____ 8. Which of the following is NOT a zero of the function?
A. 0o
B. 90o
C. 120o
D. 180o

39. APPLICATION OF RIGHT TRIANGLES
A. BEARING
B. ANGLE OF ELEVATION AND DEPRESSION

40. BEARING
Bearing - direction of one point with respect to a given point
Types of bearing:
1. True/Course bearing (T)- angle measured from north clockwise
2. Simple Bearing (S)- acute angle measured from north or south
Examples:
1. 2.
35O
E
N
W
S
T:
S:
35O
E
N
W
S
T:
S:

41. 3. 4.
35O
E
N
W
S
T:
S:
35O
E
N
W
S
T:
S:

42. Examples: Solve the following:
1. Clark’s house is 4 kilometer (km) N65O
40’E of SM Taytay while Bruce’s house is 3 km
S24O
20’E of SM Taytay. Find the distance between the two houses.
2. MV Cristina is 85 km to the East and 107 km to the south of a certain port. Find its distance
and bearing from the port.
3. Two ships left the same port at the same time, MV Katrina is going in the direction N70O
E
and MV Milagros is sailing East. MV Katrina traveled at 30 kilometer per hour (kph). After
30 min, MV Milagros was observed to be directly south of MV Katrina. Find the speed MV
Milagros.
4. Three ships are situated as follows: A is 250 miles due North of C, and B is 375 miles due
East of C. What is the simple bearing of a.) B from A b.) A from B?
5. Determine the simple and true bearing of the figure.
O 40O
23O
C
A
B
25O

43. ANGLE OF ELEVATION AND DEPRESSION

44. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
Examples: Solve the following:
1. From the top of a light house, 135 meters(m) high, it is observed that the
angle of depression of a ship is 21O. How far is the ship from the top of the
mountain?
2. Bea, standing 9m. above the ground, observes the angles of elevation and
depression of the top and bottom of the Rizal monument in Luneta as 6O50’
and 7O30’ respectively. Find the height of the monument.
3. Maru is 5 feet (ft.) tall and casts a shadow of 6 ft. on the ground. Find the
angle of elevation of the sun.
4. From two points each on the opposite sides of the river, the angles of
elevation of the top of an 80 ft. tree are 60O and 30O. The points and the tree
are in the same straight line, which is perpendicular to the river. How wide is
the river?
5. A mountain peak stands near a level plain on which two farm houses, C
and D are in straight line from the peak. The angle of depression from the
peak to C is 50O42’ and the angle of depression to D is 25O30’. The peak is
known to be 1,005 meters above the level plain. Find the distance from C to
D.

45. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
1. From the top of a light house, 135 meters(m) high, it is observed that the
angle of depression of a ship is 21O. How far is the ship from the top of the
light house?
21O
135 m.
x

46. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
2. Bea, standing 9m. above the ground, observes the angles of elevation and
depression of the top and bottom of the Rizal monument in Luneta as 6O50’
and 7O30’ respectively. Find the height of the monument.
9 m.
6O50’
7O30’
h

47. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
3. Maru is 5 feet (ft.) tall and casts a shadow of 6 ft. on the ground. Find the
angle of elevation of the sun.
5 ft.
6 ft.


48. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
4. From two points each on the opposite sides of the river, the angles of
elevation of the top of an 80 ft. tree are 60O and 30O. The points and the tree
are in the same straight line, which is perpendicular to the river. How wide is
the river?
x
80 ft.
x

49. ANGLE OF ELEVATION AND DEPRESSION PROBLEMS
5. A mountain peak stands near a level plain on which two farm houses, C and
D are in straight line from the peak. The angle of depression from the peak to
C is 50O42’ and the angle of depression to D is 25O30’. The peak is known to
be 1,005 meters above the level plain. Find the distance from C to D.
25O30’ 50O42’
25O30’
50O42’
CD
P
A
1005 m.
x x

50. QUIZ: BEARING & ANGLE OF DEPRESSION & ELEVATION
1. A plane takes off on a runway that is horizontally 915 ft. from a building, 121 ft. high.
What is the minimum angle of elevation of its take off to assure of going over the
building if it flies in a straight line? (3 PTS.)
2. A missile that was launched has angle of depression from the point of launch has
30O20’ angle of depression and was known to be 1185 ft. away from the ground. Find
the distance the missile had traveled. (3 PTS.)
3. At a considerable distance away from the base of a cliff, a surveyor found the angle
of elevation to the top of a cliff to be 70O. After moving a distance of 100 m. in a
horizontal line farther to the cliff, the angle became 50O. How high is the cliff? (3 PTS.)
4. An airplane traveled 60 km. with a bearing of . Due to the storm, it turned at From
the starting point to its current position, the distance is 90 km. How far did it travel
when it turned? (3 PTS.)
5. Determine the simple and true bearing of
OA, OB, OC AND OD. (8 PTS.)

51. QUIZ: BEARING & ANGLE OF DEPRESSION & ELEVATION
1. A plane takes off on a runway that is horizontally 915 ft. from a building, 121 ft. high.
What is the minimum angle of elevation of its take off to assure of going over the
building if it flies in a straight line? (3 PTS.)
121 ft.
915 ft.
tanθ =
121
915
𝜽 = 𝟕 𝑶
𝟑𝟏′

52. QUIZ: BEARING & ANGLE OF DEPRESSION & ELEVATION
2. A missile that was launched has angle of depression from the point of launch has
30O20’ angle of depression and was known to be 1185 ft. away from the ground. Find
the distance the missile had traveled. (3 PTS.)
1185 ft.
30O20’
sin30O20′ =
1185
𝑥
𝒙 = 𝟐𝟑𝟒𝟔. 𝟒𝟎 𝒇𝒕.
x
30O20’

53. QUIZ: BEARING & ANGLE OF DEPRESSION & ELEVATION
3. At a considerable distance away from the base of a
cliff, a surveyor found the angle of elevation to the top
of a cliff to be 70O. After moving a distance of 100 m. in
a horizontal line farther to the cliff, the angle became
50O. How high is the cliff? (3 PTS.)
tan70O =
ℎ
𝑥
ℎ = 𝑥𝑡𝑎𝑛70 𝑂
ℎ = 2.75𝑥①
tan50O =
ℎ
𝑥 + 100
ℎ = (𝑡𝑎𝑛50 𝑂)(𝑥 + 100)
ℎ = 1.19𝑥 + 100𝑡𝑎𝑛50 𝑂
ℎ = 1.19𝑥 + 119.18②
①=②
ℎ = ℎ
2.75𝑥 = 1.19𝑥 + 119.18
1.56𝑥 = 119.18
𝑥 = 76.40③
③to①
ℎ = 2.75(76.40)
𝒉 = 𝟐𝟏𝟎. 𝟏𝟎 𝒎
h
50O 70O
100 m x

54. PROVING IDENTITIES

55. SUGGESTIONS FOR PROVING IDENTITIES
1. Learn well the formulas given above (or at least, know how to
find them quickly).
2. Choose the more complicated side and start transforming it so
that it has the same form as the simpler side.
3. Sometimes, it is more convenient to transform each side
simultaneously into same equivalent form (METHOD 2).
4. Try to express everything in terms of sines and cosines.
5.Instead of applying suggestion 4, sometimes advantageous to
convert everything into a single function only.
6. Have an open mind in using algebraic processes to facilitate
proving.
7. You may introduce a desired factor to obtain a particular
expression.
8. Look for ways to use identities 6, 7 and 8 or one of its other
forms.
9.Set in mind the result you want in the end.

56. sin cos
tan cot
sec csc
1
2 2
2
2
2
2

59. 3. 𝑐𝑠𝑐2
𝜃 − 𝑐𝑠𝑐2
𝜃𝑐𝑜𝑠2
𝜃 = 1

60. 1.
𝑠𝑒𝑐𝜃+1
𝑠𝑒𝑐𝜃−1
=
1+𝑐𝑜𝑠𝜃
1−𝑐𝑜𝑠𝜃
2.
1−𝑐𝑜𝑡2 𝜃
1+𝑐𝑜𝑡2 𝜃
= 𝑠𝑖𝑛2
𝜃 − 𝑐𝑜𝑠2
𝜃
3.
1
1+𝑐𝑜𝑠𝑎
+
1
1−𝑐𝑜𝑠𝑎
= 2𝑐𝑠𝑐2 𝑎
4.
𝑠𝑖𝑛𝛽
1+𝑐𝑜𝑠𝛽
+
1+𝑐𝑜𝑠𝛽
𝑠𝑖𝑛𝛽
= 2𝑐𝑠𝑐𝛽
5. 𝑐𝑠𝑐4
𝜃 − 𝑐𝑜𝑡4
𝜃 = 𝑐𝑠𝑐2
𝜃 + 𝑐𝑜𝑡2
𝜃
6.
𝑡𝑎𝑛3 𝑥+𝑠𝑖𝑛𝑥𝑠𝑒𝑐𝑥−𝑠𝑖𝑛𝑥𝑐𝑜𝑠𝑥
𝑠𝑒𝑐𝑥−𝑐𝑜𝑠𝑥
= 𝑡𝑎𝑛𝑥𝑠𝑒𝑐𝑥 + 𝑠𝑖𝑛𝑥

61. SUM AND DIFFERENCE OF TWO
ANGLES

66. LOGARITHMS