Download to read offline
Uploaded bySiti Nur Khotimah
Trigonometry 2
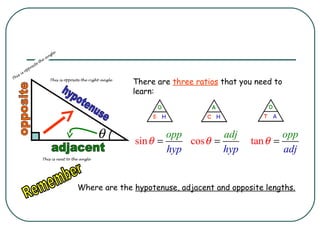
This document discusses trigonometric ratios and solving trigonometric equations. It provides the definitions of sine, cosine, and tangent ratios relating the opposite, adjacent, and hypotenuse sides of a right triangle. An example problem is worked through to solve for the unknown side of a triangle using the sine ratio, substituting known values and rearranging the equation by multiplying both sides by the variable. A second example is presented using the tangent ratio to solve another trigonometric equation for the unknown side.
More Related Content
Trigonometry 2
- 1. i Th s o pp so i e th ite s . le ng a This is oppositethe right-angle θ There are three ratios that you need to learn: opp adj sin θ = cos θ = hyp hyp opp tan θ = adj This is next to the angle Where are the hypotenuse, adjacent and opposite lengths.
- 2. You need tolabel all the lengths of the triangle. The adjacent is not needed in this question; the question is only using opposite and hypotenuse. x 10 cm 30o
- 3. You need tolabel all the lengths of the triangle. The adjacent is not needed in this question; the question is only using opposite and hypotenuse. x 10 cm 30o
- 4. sin θ = opp adj cosθ = hyp hyp tan θ = We need to use the sine ratio and substitute the values/variables that we know. sin θ = opp hyp x sin 30 = 10 opp adj x 10 cm 30o
- 5. We need tosolve the equation (*). opp sin θ = hyp x ( *) sin 30 = 10 We can think of this as: OR 10 cm x 30o x → ÷10 → sin 30 5 ¬ ×10 ¬ sin 30 rearrange the equation (*) by multiplying both sides by x. x 10 × sin 30 = × 10 10 ⇒ 10 × sin 30 = x 5= x
- 6. These two trianglesare very different. ⇒ The variable x will be on the denominator This is an example of where we have to solve an equation with the variable on the denominator, so multiply both sides by x. 10 x × sin 30 = × x x opp sin θ = hyp 10 sin 30 = x still need to get x on its own, so x × sin 30 = 10 divide both sides by sin30 10 10 x= = = 20 sin 30 0.5
- 7. 15cm opp tan θ = adj x 30o 15 x× tan 30 = × x x x × tan 30 = 15 tan 30 tan 30
- 8. 15cm opp tan θ = adj x 30o 15 tan30 = x 15 ⇒ x × tan 30 = × x x ⇒ x × tan 30 = 15 15 x= ⇒ tan 30