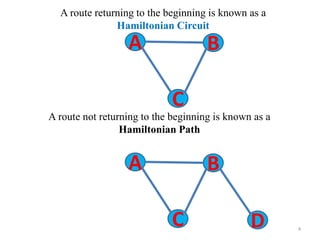
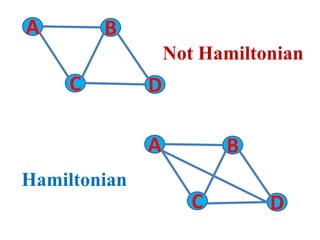
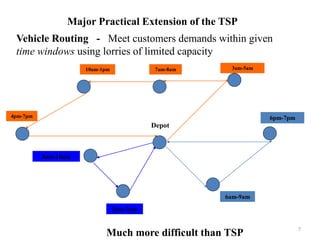
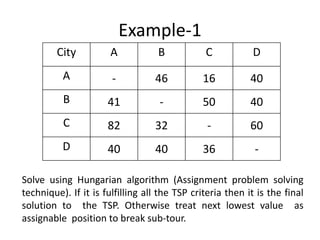
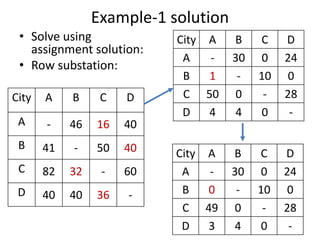
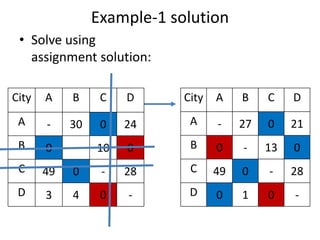
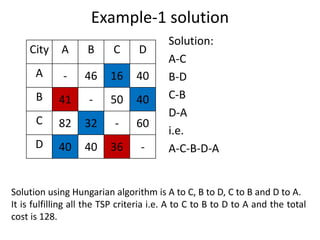
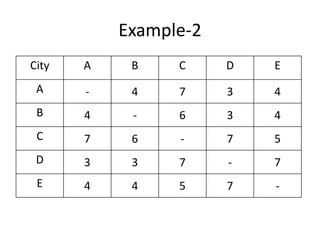
The document discusses the travelling salesman problem (TSP) which aims to find the shortest route for a salesman to visit each city in a list only once and return to the original city. It provides examples of different paths through cities and notes there are (n-1)! possible solutions when there are n cities. The document outlines real-world applications of TSP and methods for solving it, including trying every possibility for small problems or using optimization methods for larger problems. It gives two examples of TSP problems and shows the solutions using an assignment algorithm and considering additional constraints to avoid sub-tours.

1. Travelling Salesman Problem
(TSP)

2. A
E
D
C
B

3. Different paths to previous example
• A-B-C-D-E-A
• B-A-C-D-E-B
• B-C-A-D-E-B
• B-C-D-A-E-B
• B-D-C-A-E-B
• B-E-D-C-A-B
• C-B-A-D-E-C
• D-C-B-A-E-D
• D-B-C-A-E-D
• …..
There are (n-1)!
Solutions when you
have n nodes.

4. 4
A route returning to the beginning is known as a
Hamiltonian Circuit
A route not returning to the beginning is known as a
Hamiltonian Path
A
C
B
A
C
B
D

5. Hamiltonian
A
C
B
D
A
C
B
D
Not Hamiltonian

6. Real-Life Applications
• It’s not likely anyone would want to plan a bike trip to 25 cities
• But the solution of several important “real world” problems is the
same as finding a tour of a large number of cities
– transportation: school bus routes,
service calls, delivering meals, ...
– manufacturing: an industrial robot
that drills holes in printed circuit
boards
– VLSI (microchip) layout
– communication: planning new
telecommunication networks
– connecting together computer
components using minimum
wire length

7. 7
8am-10am
2pm-3pm
3am-5am7am-8am10am-1pm
4pm-7pm
Major Practical Extension of the TSP
Vehicle Routing - Meet customers demands within given
time windows using lorries of limited capacity
Depot
6am-9am
6pm-7pm
Much more difficult than TSP

8. TSP Formulation
• TSP problem formulation is look like
assignment problem formulation with
additional constraints.
𝑥𝑖𝑗 = 0 𝑂𝑟 1
A
E
D
C
B

9. Additional constraints for TSP
1. Sub tour of length 0 (e.g. from city A to city A):
2. Sub tour of length 1 (e.g. from city A to city B and then city B to city A):
3. Sub tour of length 2 (e.g. from city A to city C via city B and then city C to
city A without travelling other cities):
4. And so on
5. No city is visited twice before the tour of all cities is completed.
A B
A B
C
A

10. 10
Solution Methods
I. Try every possibility (n-1)! possibilities – grows faster
than exponentially
If it took 1 microsecond to calculate each possibility
takes 10140 centuries to calculate all possibilities when n = 100
II. Optimising Methods obtain guaranteed optimal
solution, but can take a very,
very, long time
III. Heuristic Methods obtain ‘good’ solutions ‘quickly’
by intuitive methods.
No guarantee of optimality

11. Example-1
City A B C D
A - 46 16 40
B 41 - 50 40
C 82 32 - 60
D 40 40 36 -
Solve using Hungarian algorithm (Assignment problem solving
technique). If it is fulfilling all the TSP criteria then it is the final
solution to the TSP. Otherwise treat next lowest value as
assignable position to break sub-tour.

12. Example-1 solution
• Solve using
assignment solution:
• Row substation:
City A B C D
A - 46 16 40
B 41 - 50 40
C 82 32 - 60
D 40 40 36 -
City A B C D
A - 30 0 24
B 1 - 10 0
C 50 0 - 28
D 4 4 0 -
City A B C D
A - 30 0 24
B 0 - 10 0
C 49 0 - 28
D 3 4 0 -

13. Example-1 solution
• Solve using
assignment solution:
City A B C D
A - 30 0 24
B 0 - 10 0
C 49 0 - 28
D 3 4 0 -
City A B C D
A - 27 0 21
B 0 - 13 0
C 49 0 - 28
D 0 1 0 -

14. Example-1 solution
Solution:
A-C
B-D
C-B
D-A
i.e.
A-C-B-D-A
City A B C D
A - 46 16 40
B 41 - 50 40
C 82 32 - 60
D 40 40 36 -
Solution using Hungarian algorithm is A to C, B to D, C to B and D to A.
It is fulfilling all the TSP criteria i.e. A to C to B to D to A and the total
cost is 128.

15. Example-2
City A B C D E
A - 4 7 3 4
B 4 - 6 3 4
C 7 6 - 7 5
D 3 3 7 - 7
E 4 4 5 7 -

16. Example-2 Solution
Solution: The optimum
assignment cost is 20.
A-D
B-A
C-E
D-B
E-C
i.e. two sub tours: A-D-B-A and
C-E-C
City A B C D E
A - 0 2 0 0
B 0 - 1 0 0
C 2 1 - 3 0
D 0 0 3 - 4
E 0 0 0 4 -
• It is not fulfilling all the TSP criteria because A to D to B to A without passing through C and E.
• The next minimum non-zero element in the cost matrix is 1. So bring 1 into the solution. But the element 1
occurs at two places. Hence consider all cases separately until get an optimal solution.
• Start with making an assignment at (B, C) instead of zero assignment at (B, A). The resulting solution is A to D to
B to C to E to A.
• When an assignment is made at (C, B) instead of zero assignment at (C, E), the resulting solution is A to E to C
to B to D to A.
• Both the case total cost is 21.