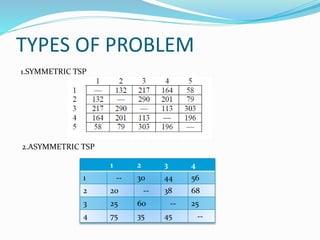
The document discusses the travelling salesman problem (TSP). TSP involves finding the shortest possible route for a salesman to visit each city in a set and return to their starting point. The problem was first studied in the 1800s and became increasingly popular in scientific circles in the 1950s-60s. TSP is an NP-complete optimization problem with many real-world applications like delivery routing. Exact methods to solve TSP take too long, so heuristic methods provide good but not necessarily optimal solutions more quickly. The objective is to minimize the total distance traveled between cities, and TSP problems can be symmetric or asymmetric depending on whether distances between cities are the same in both directions.

1. By,
SHAILESH JADHAV
RAHUL CHAUGULE
v VIRAJ PATIL

2. HISTORY
 In the 1800s, Travelling salesman problems were looked by Sir William
Rowan Hamilton and Thomas Kirkman.
 Hassler Whitney at Princeton University introduced the name
travelling salesman problem
 In the 1950s and 1960s, the problem became increasingly popular in
scientific circles in Europe and the USA.
 Richard M. Karp showed in 1972 that the Hamiltonian cycle problem
was NP-complete.

3. INTRODUCTION
 The travelling salesman problem consists of a salesman and a set of cities.
The salesman has to visit each one of the cities starting from a certain one
(e.g. the hometown) and returning to the same city. The challenge of the
problem is that the travelling salesman wants to minimize the total length of
the trip.
 Travelling salesman problem is one of the most extensively studied
optimization problem that is used to find the shortest possible route.
 TSP has many applications including following:
1. The delivery of meals to office persons.
2. Manufacture of microchips.
3. The routing of courier trucks.
4. The routing of any salesman.

4. SOLVING METHODS
 Try every possibility: (n-1)!Possibilities- Takes longer time.
 Optimising Methods: obtain guaranteed optimal solution.
 Heuristic Method: obtain ‘good’ solution ‘quickly’ by intuitive methods
.No guarantee of optimality.

5. Objective function
The mathematical formulation of the problem can be as in Eq.
Where,
d(i,j)- Distance travelled from city ‘i’ to city ‘j’.
x(i.j) –cost of travel from city ‘i’ to city ’j’.
min
x
x(i, j)d(i, j)
j 1
n
i 1
n

s.t.
x(i, j) 1, i  1,2,...,n
j 1
n

x(i, j) 1, j  1,2,...,n
i 1
n

x(i, j)  S  1, S  {1,2,...,n}
i , jS
n

x(i, j) {0,1}

6. TYPES OF PROBLEM
1.SYMMETRIC TSP
2.ASYMMETRIC TSP
1 2 3 4
1 -- 30 44 56
2 20 -- 38 68
3 25 60 -- 25
4 75 35 45 --

7. CONCLUSION
 Travelling salesman problem is one of the most extensively studied
optimization problem that is used to find the shortest possible route.
 By knowing or solving the Travelling salesman problem we get the
optimal travelling distance/path cost.
 We should know which appropriate method to be used while solving
TSP.