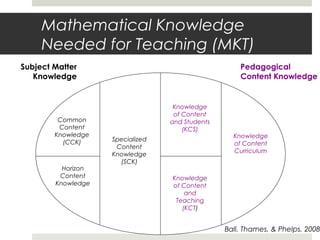
This document summarizes a presentation on developing mathematical knowledge for teaching (MKT) through analyzing tasks and curriculum. It discusses the game "Close to 100" and examines opportunities for student mathematical discourse. It also outlines frameworks for MKT and the mathematical tasks of teaching. The presentation considers how to draw out and deepen student thinking within curriculum and promotes building an environment where students engage in authentic mathematical inquiry, exploration, and negotiation.

1. Developing the Mathematical
Knowledge Needed for Teaching
(MKT) through Analyzing and
Deepening Tasks/Curriculum
Nicole Miller Rigelman
Portland State University
Teachers of Teachers of Mathematics
September 12, 2009

2. Close to 100
The object of the game is to create double-digit numbers that
sum as close to 100 as possible. Each game has five rounds.
For round 1, deal six cards to each player. Players then choose
any four of their six cards to make two two-digit numbers that,
when added, come as close to 100 as possible. Wild cards can
be assigned any value. Players record their numbers and total
on their score sheets. The player’s score is the difference
between the total and 100. (102 and 98 are both scored as 2.)
The used cards are discarded and four new cards are dealt to
each player. Each player will have 6 cards at the beginning of
a round, two that are left from the previous round and four that
are new.
At the end of five rounds the player with the lowest total score
wins.

3. Close to 100 Strategies
•
•
•

4. About this Session
 Doing some math; playing Close to 100.
 Framing our Work
 Examining the opportunities for student
mathematical discourse within the curriculum
as written.
 Analyze video clip of students at work.
 Considering general strategies for drawing out
and deepening student thinking and reasoning.

5. The Principles & Standards say…

7. Mathematical Tasks of Teaching
Ball, Thames, & Phelps, 2008
 Presenting mathematical ideas
 Responding to students “why” questions
 Finding an example to make a specific mathematical
point
 Linking representations to underlying ideas and to other
representations
 Connecting a topic being taught to topics from prior of
future years
-

8.  Explaining mathematical goals and purposes to parents
 Appraising and adapting mathematical content of
textbooks
 Modifying tasks to be either easier or harder
 Evaluating the plausibility of students’ claims (often
quickly)
 Giving or evaluating mathematical explanations
 Choosing and developing useable definitions
 Using mathematical notation and language and
critiquing its use
 Asking productive mathematical questions
 Selecting representations for particular purposes
 Inspecting equivalencies

9. Mathematical Knowledge
Needed for Teaching (MKT)
Subject Matter
Knowledge
Common
Content
Knowledge
(CCK)
Horizon
Content
Knowledge
Pedagogical
Content Knowledge
Knowledge
of Content
and Students
(KCS)
Specialized
Content
Knowledge
(SCK)
Knowledge
of Content
Curriculum
Knowledge
of Content
and
Teaching
(KCT)
Ball, Thames, & Phelps, 2008

10. Why Student Mathematical
Discourse?

11. Why Student Mathematical Discourse?
 The discourse of a classroom – the
ways of representing, thinking,
talking, agreeing, and disagreeing
– is central to what and how
students learn about mathematics.
- NCTM, 2007,
p. 46

12. The Intended Curriculum
Private Think Time
 Imagine a group of 4th graders engaged in this activity.
Predict the levels of math talk you would hear. Record
examples of what you think students might say in the
cells of the Discourse Analysis Tool.
Deepening the Discourse
 Recognizing the goal of promoting higher-levels of
student mathematical discourse, what might you do to
deepen the math talk?

14. Mathematical Tasks of Teaching
Ball, Thames, & Phelps, 2008
 Presenting mathematical ideas
 Responding to students “why” questions
 Finding an example to make a specific mathematical
point
 Linking representations to underlying ideas and to other
representations
 Connecting a topic being taught to topics from prior of
future years
-

15.  Explaining mathematical goals and purposes to parents
 Appraising and adapting mathematical content of
textbooks
 Modifying tasks to be either easier or harder
 Evaluating the plausibility of students’ claims (often
quickly)
 Giving or evaluating mathematical explanations
 Choosing and developing useable definitions
 Using mathematical notation and language and
critiquing its use
 Asking productive mathematical questions
 Selecting representations for particular purposes
 Inspecting equivalencies

16. Close to 1000
Close to 1000 is similar, but the number of cards dealt is
different. Players start with 8 cards, and lay out six of them
to make two three-digit numbers that add as close to 1000
as possible.
A game consists of 5 rounds and the player with the lowest
score at the end of five rounds is the winner.

17. What if we played…
 Close to 10,000 with two four-digit numbers,
Close to 100,000 with two five digit numbers,
etc. Work to describe a general strategy for all
games involving two addends whose sum is
close to a power of 10 or list some components
of such a general strategy.

18. Principles & Standards remind us…

19. Developing the Mathematical
Knowledge Needed for Teaching
 What ideas/tools are you taking away for developing the
mathematical knowledge needed for teaching?
 What questions remain … and what might you do to
work on answering the questions?

20. Building and Sustaining Student
Mathematical Discourse
 Teachers need to create an environment in which
students build a “personal relationship” with
mathematics. Three key elements need to be in this
environment.
1. Students need to engage in authentic mathematical
inquiries.
2. Students must act like mathematicians as they explore
ideas and concepts.
3. Students need to negotiate. The meanings of, and
connections among, these mathematical ideas with
other students in the class.
- D’Ambrosio, 1995

21. Questions?
Nicole Miller Rigelman
rigelman@pdx.edu