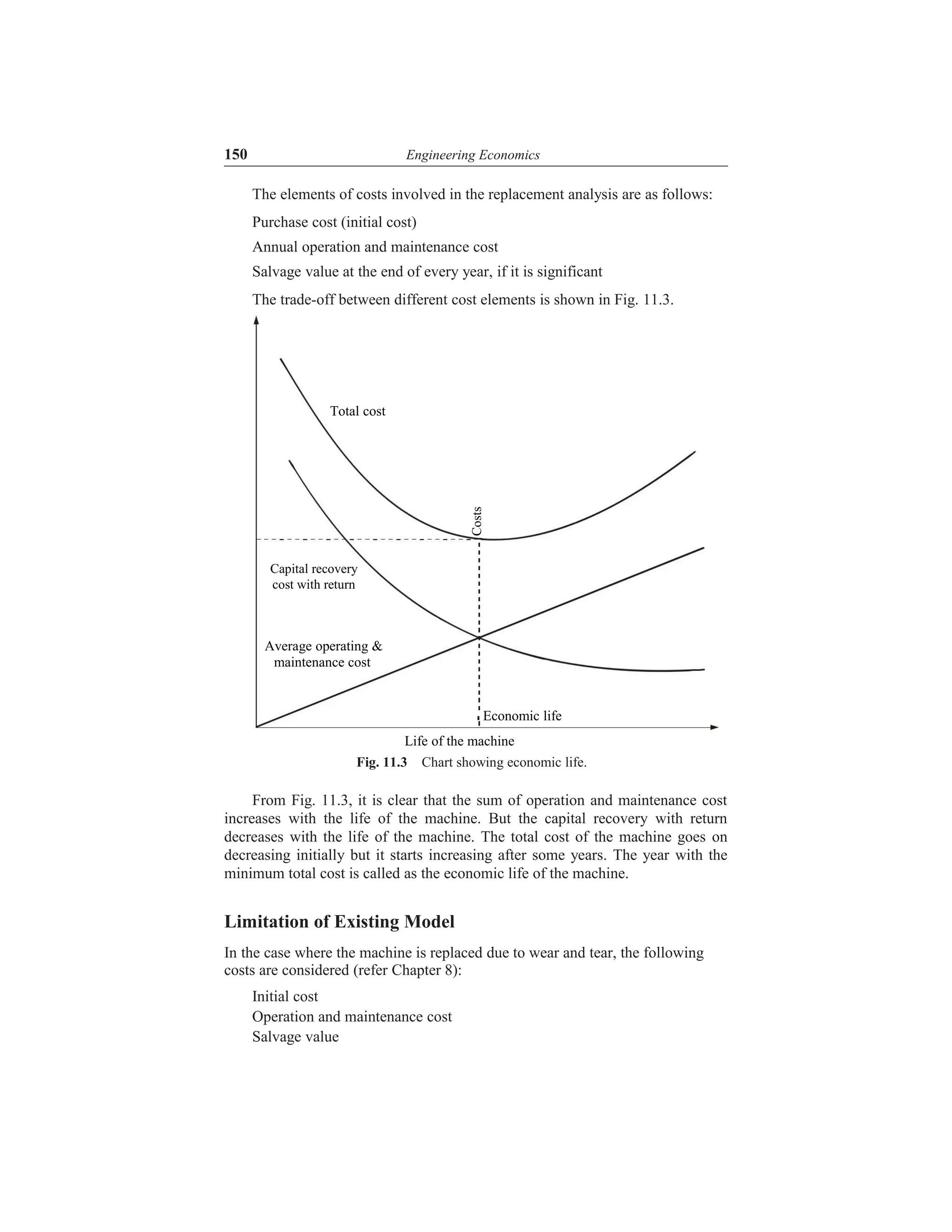
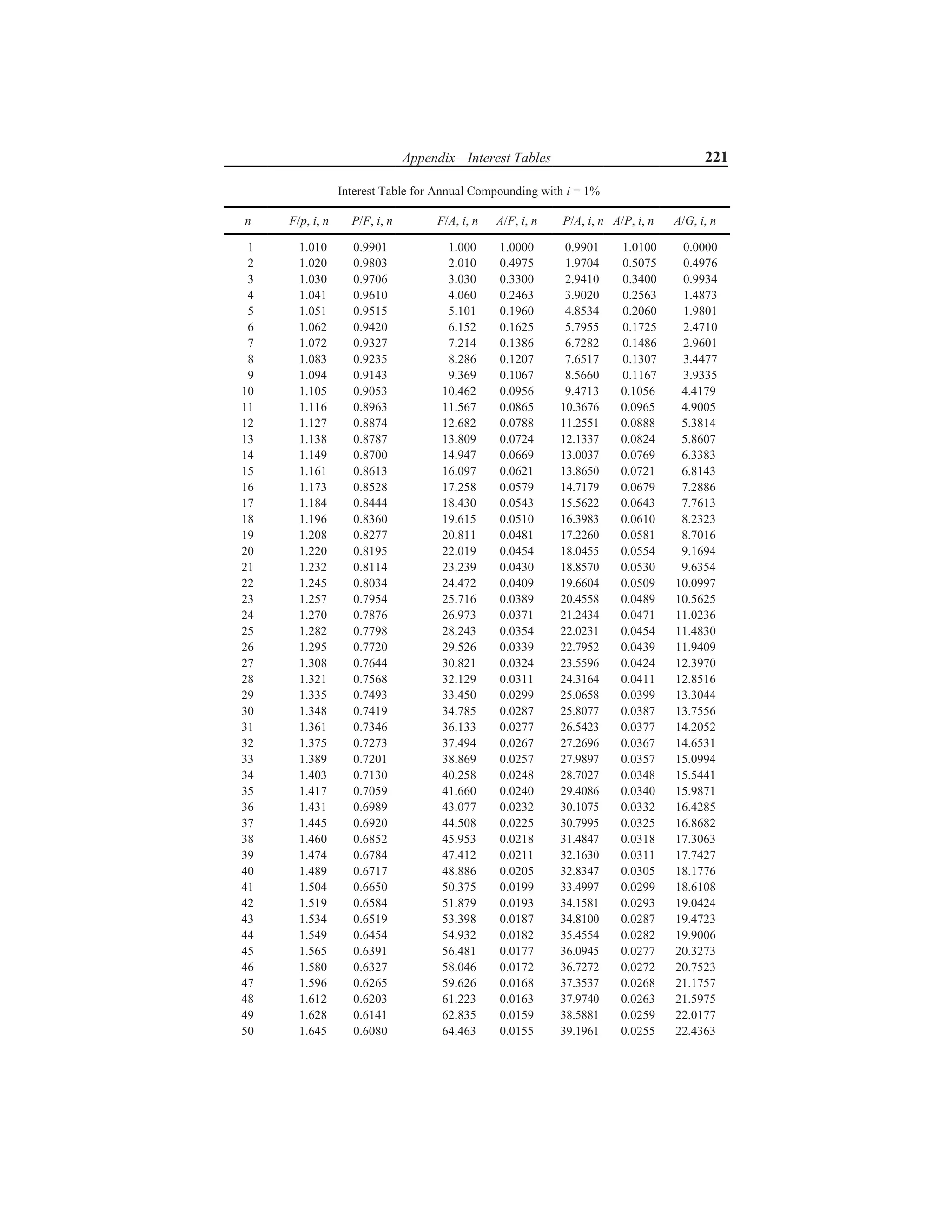
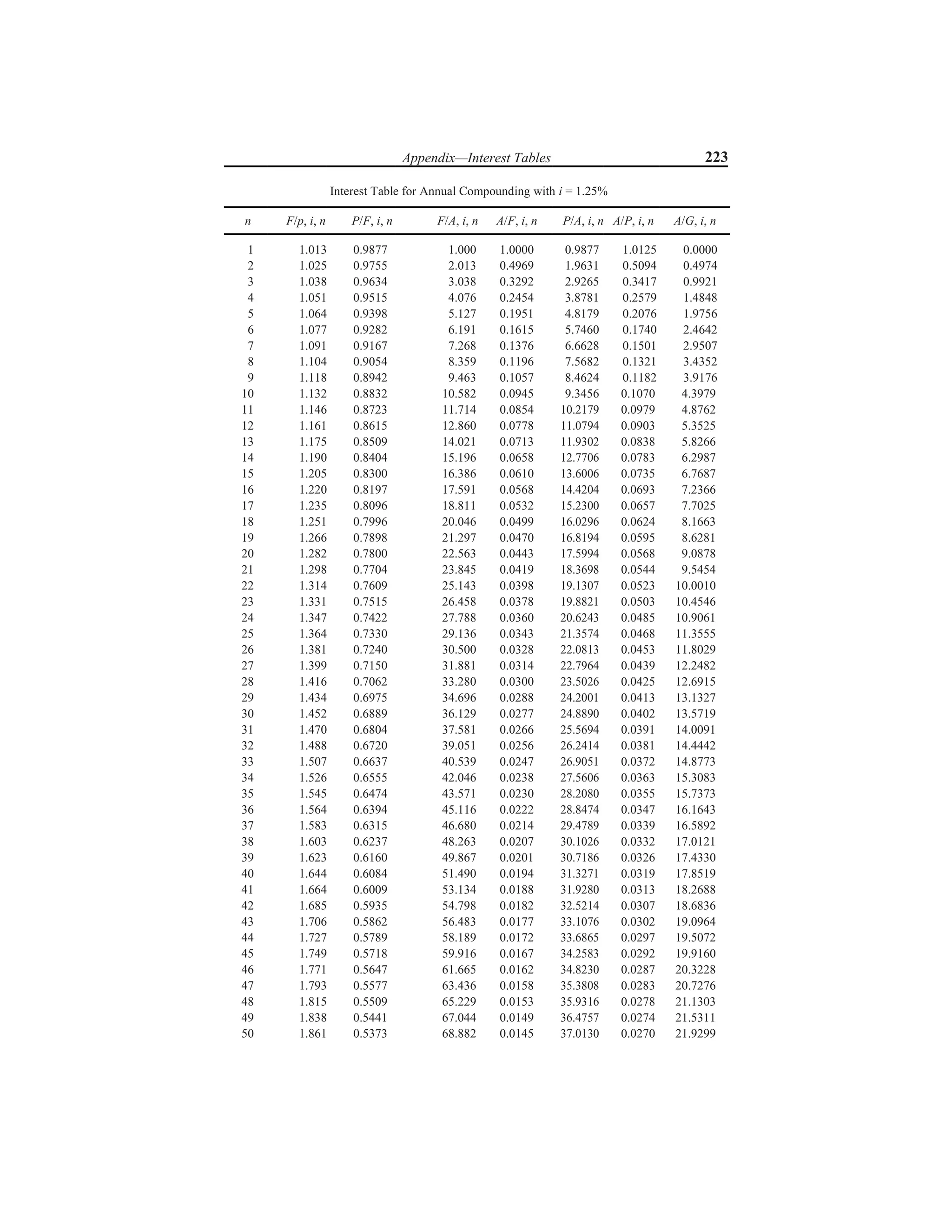
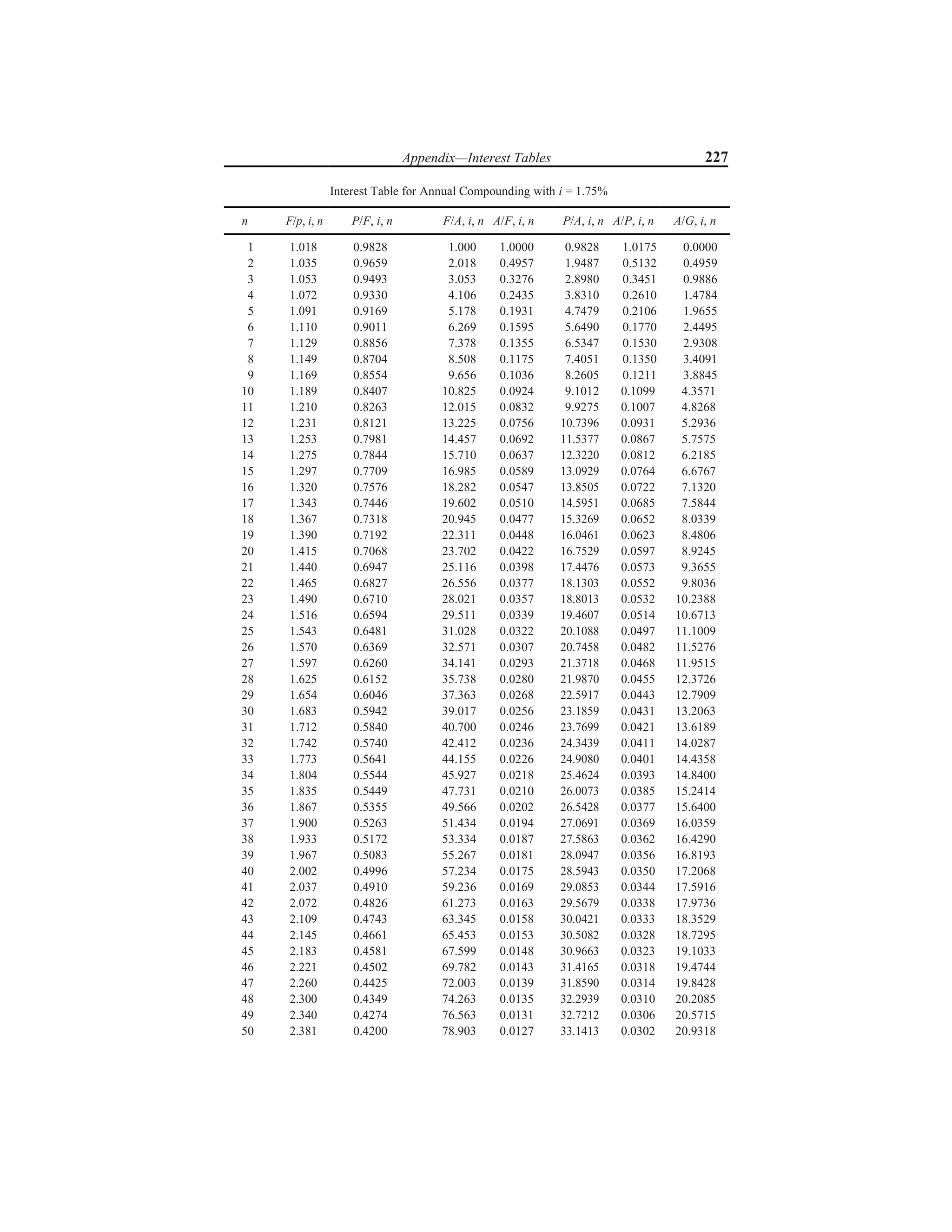
The document discusses various interest formulas and their applications. It introduces compound interest, where interest is calculated on both the principal amount and accumulated interest from previous periods. Formulas are provided to calculate the compound amount, present worth amount, equal payment series compound amount, equal payment series sinking fund, equal payment series present worth amount, and equal payment series capital recovery amount. An example calculation is shown for each formula to illustrate how to use it to solve investment problems.