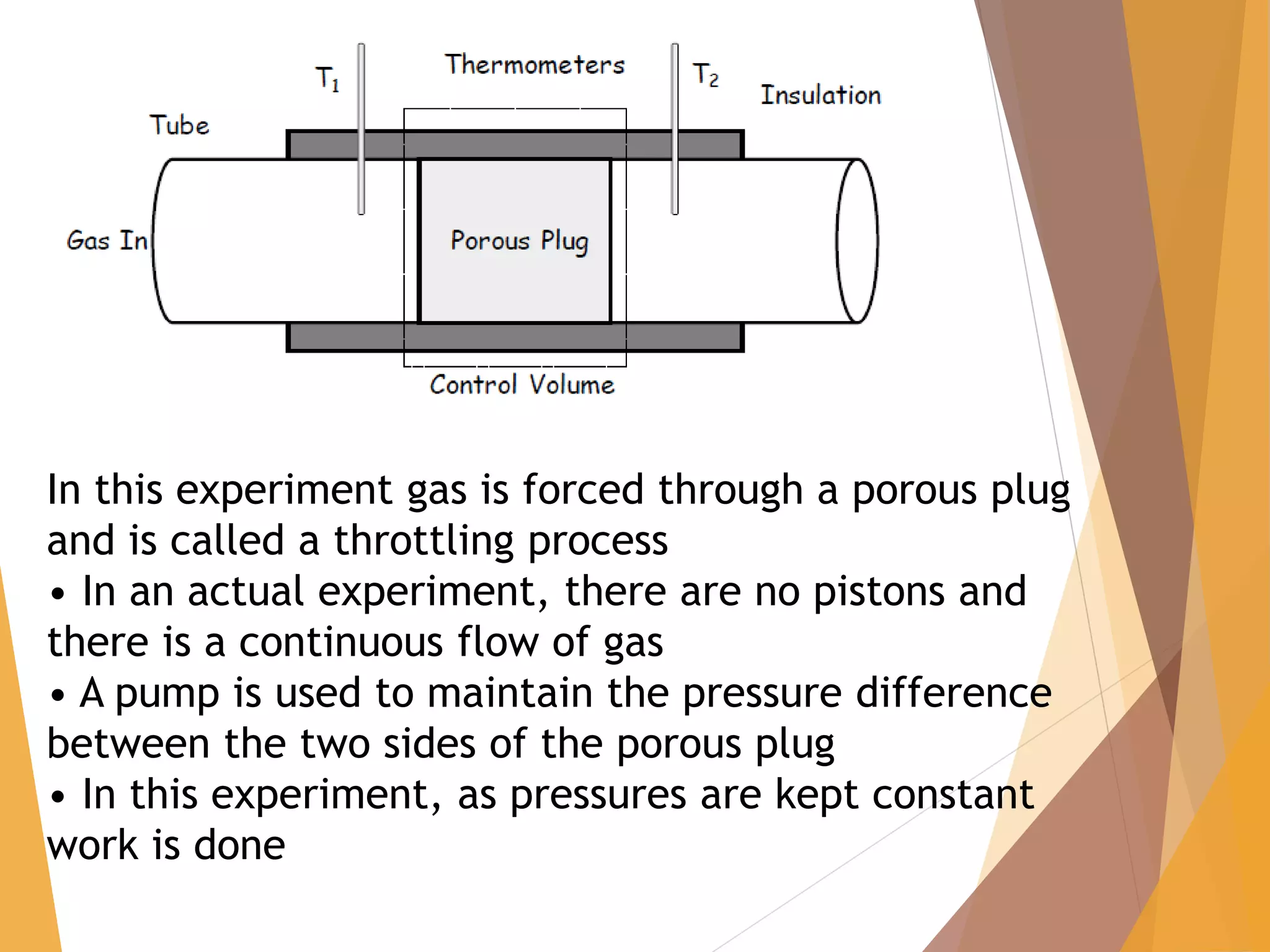
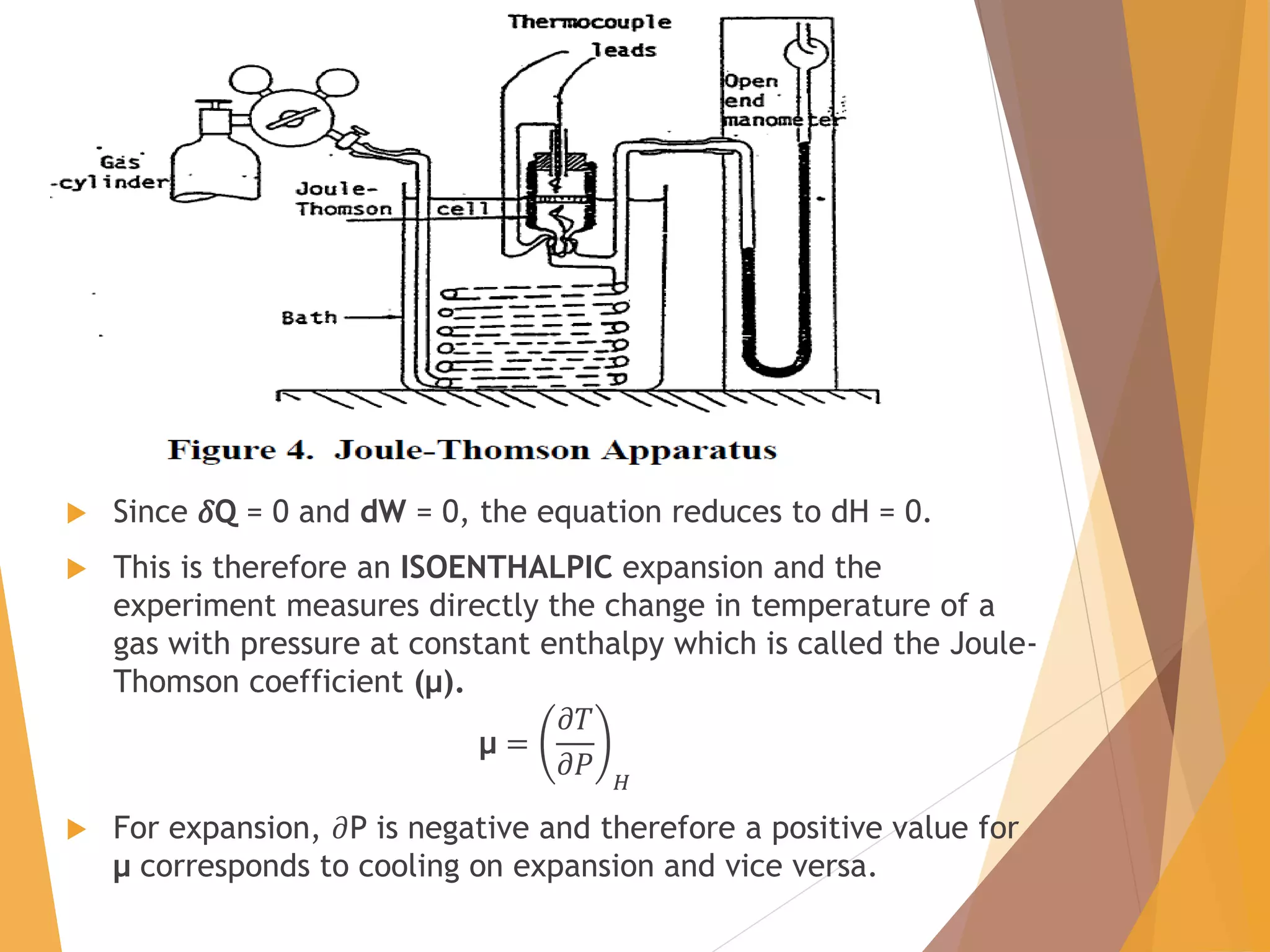
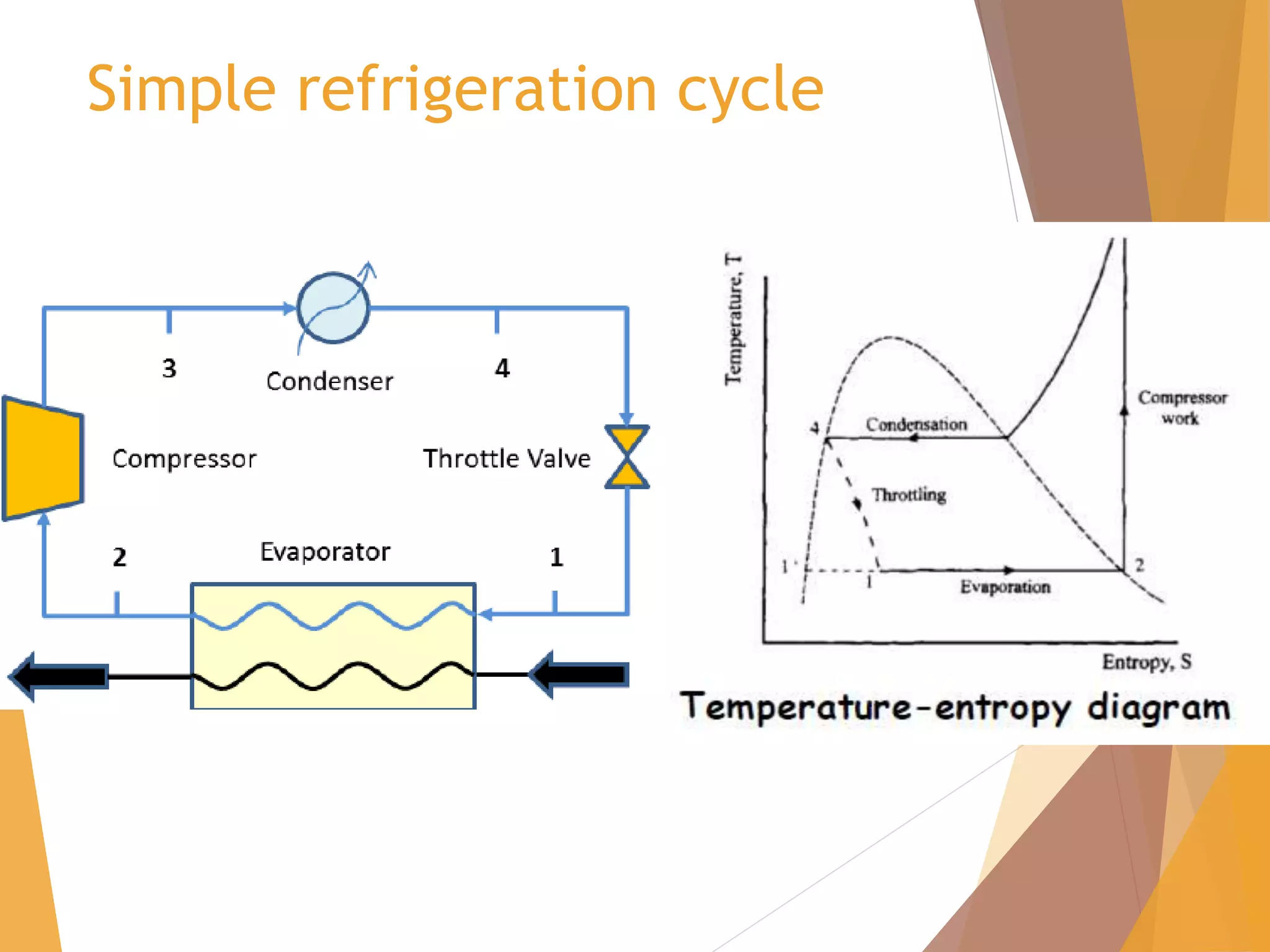
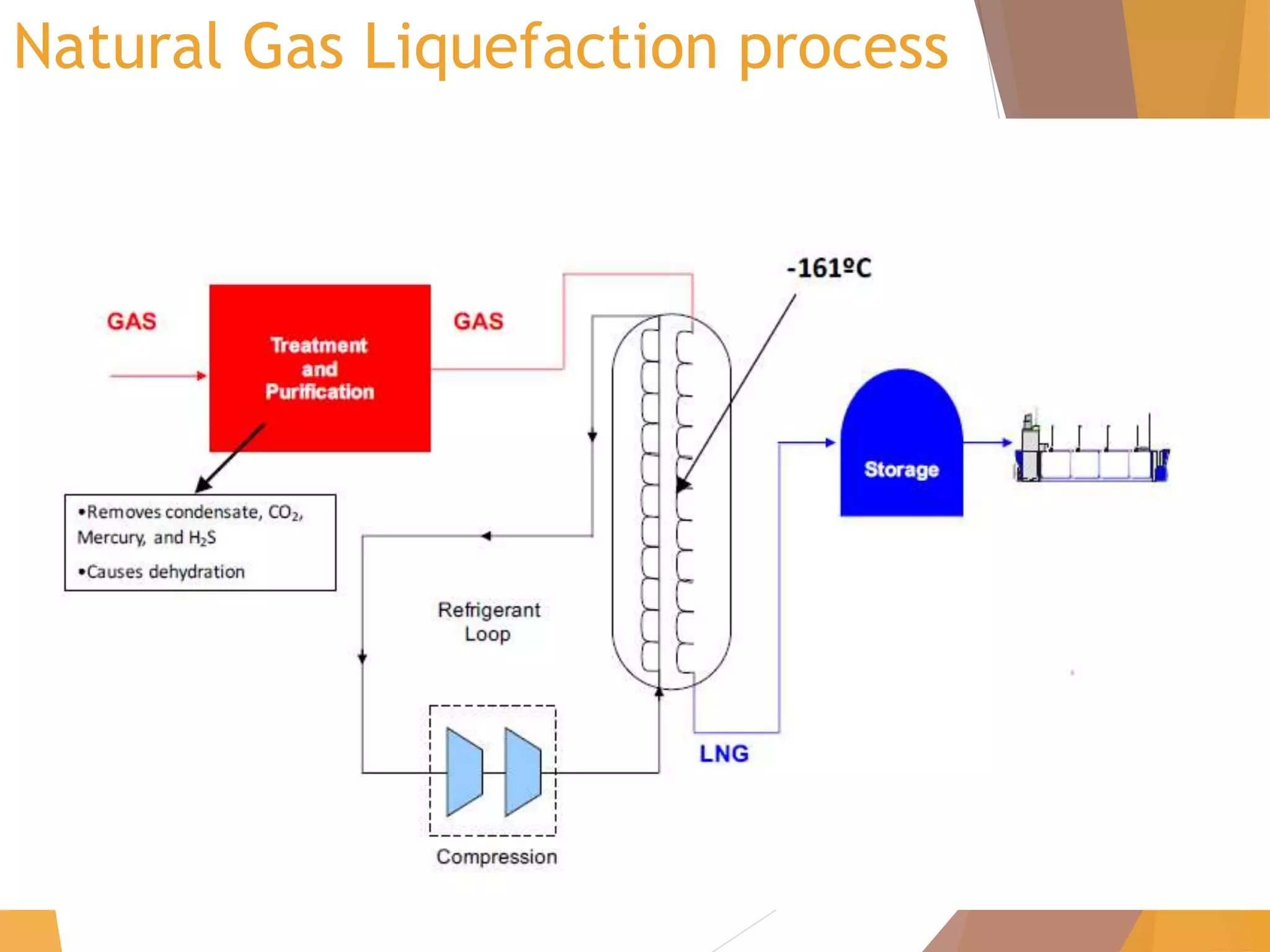
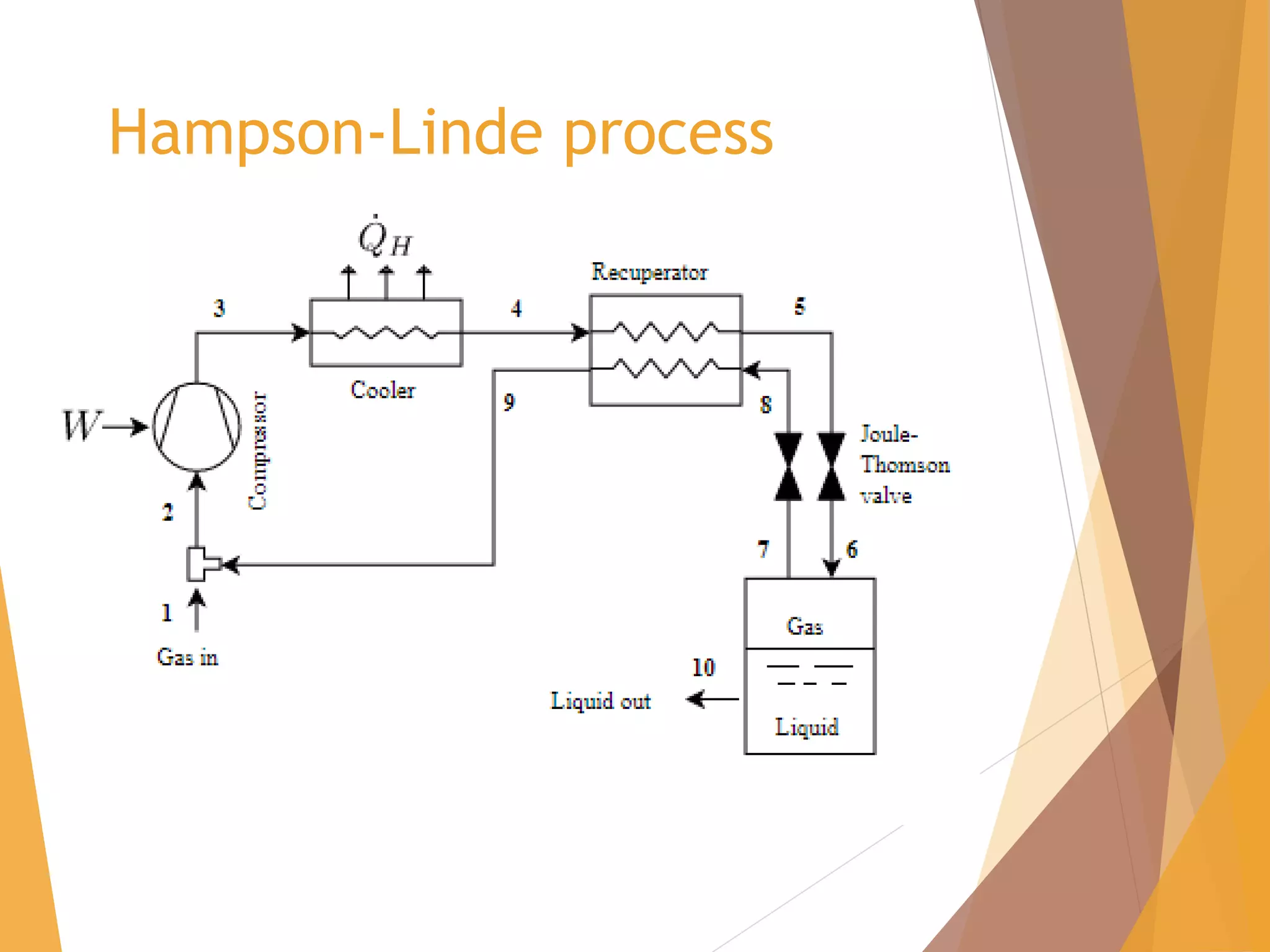
The document discusses throttling processes and the Joule-Thomson effect. It defines throttling as the passage of a fluid through a narrow constriction, causing a reduction in pressure and increase in volume. The Joule-Thomson experiment involves forcing a gas through a porous plug in a throttling process while maintaining constant pressures and measuring the temperature change. The experiment shows that for some gases, temperature decreases with decreasing pressure (positive Joule-Thomson coefficient), while for others it increases, depending on conditions. Applications of throttling discussed include determining steam dryness, controlling turbine speed, refrigeration, gas liquefaction, and cryogenic processes.

1. GOVERNMENT
ENGINEERING
COLLEGE
Subject: CHEMICAL ENGINEERING
THERMODYNAMIC (2140502)
Topic: Throttling and Joule-Thompson
Coefficient and its Applications

2. 1 Bhadja Anand C. 160190105006
2 Davra Dharmik G. 160190105016
3 Moradiya Milan L. 160190105043
4 Pandav Mukund G. 160190105049
5 Papaniya Hitesh L. 160190105051
Submitted By:

3. Throttling & The Joule-
Thomson Experiment
 Throttling process involves the passage of a higher
pressure fluid through a narrow constriction.
 The effect is the reduction in pressure and increase in
volume
• This process is adiabatic as no heat flows from and to
the system, but it is not reversible.
• It is not an isentropic process
• The entropy of the fluid actually increases
 Such a process occurs in a flow through a porous plug, a
partially closed valve and a very narrow orifice.

4. In this experiment gas is forced through a porous plug
and is called a throttling process
• In an actual experiment, there are no pistons and
there is a continuous flow of gas
• A pump is used to maintain the pressure difference
between the two sides of the porous plug
• In this experiment, as pressures are kept constant
work is done

5.  The pump maintains the pressures 𝑃𝑖 and 𝑃𝑓
 In the experiment 𝑃𝑖, 𝑇𝑖 and 𝑇𝑖 are set and 𝑇𝑓 is measured
 Consider a series of experiments in which 𝑃𝑖 and 𝑇𝑖 are constant
(𝐻𝑖 constant) and the pumping speed is changed to change 𝑃𝑓
and hence 𝑇𝑓
 Since the final enthalpy does not change, we get points of
constant enthalpy

6. Work Done
𝑊 =
𝑉 𝑖
0
𝑃𝑖 𝑑𝑉 +
0
𝑉 𝑓
𝑃𝑓 𝑑𝑉
= 𝑃𝑓 𝑉𝑓 − 𝑃𝑖 𝑉𝑖
The overall change in internal energy of the gas is
ߜQ = dU + dW
For Adiabatic Expansion ߜQ is 0
0 = 𝑈𝑓 − 𝑈𝑖 + 𝑃𝑓 𝑉𝑓 − 𝑃𝑖 𝑉𝑖
𝑈𝑓 + 𝑃𝑓 𝑉𝑓 = 𝑈𝑖 + 𝑃𝑖 𝑉𝑖
But Enthalpy is
H = U + PV
𝐻𝑓 = 𝐻𝐼
Hence, in a Throttling process, enthalpy is conserved.

7.  Since ߜQ = 0 and dW = 0, the equation reduces to dH = 0.
 This is therefore an ISOENTHALPIC expansion and the
experiment measures directly the change in temperature of a
gas with pressure at constant enthalpy which is called the Joule-
Thomson coefficient (μ).
μ =
𝜕𝑇
𝜕𝑃 𝐻
 For expansion, 𝜕P is negative and therefore a positive value for
μ corresponds to cooling on expansion and vice versa.

8.  The gas which is initially at a
state represented by the point
P as shown in fig., is
undergoing Joule-Thompson
Expansion.
 It will experience the rise in
temperature till the point Q is
reached, and thereafter the
temperature decreases with
further decreases in pressure.
 The slope is the isenthalpy is
equal to the Joule-Thompson
coefficient as per the
relation.
 It is positive only in the region
where pressure is less than
that of Q and is Zero at point
Q, where the isenthalpy
exhibits a maximum.
A smooth curve is placed through the
points yielding an isenthalpic curve

9. μ
μ < 0 temperature increases
μ = 0 temperature remains constant
μ > 0 temperature decreases

11.  This also tells us that we cannot just use any gas at any set of
pressures to make a refrigerator, for example
• - At a given pressure, some gases may be cooling (m > 0) but
others may be heating (m < 0)
 The proper choice of refrigerant will depend on both the
physical properties, esp. the Joule-Thompson coefficient as
well as the mechanical capacity of the equipment being used.
 Thus, we cannot just exchange our ozone-depleting freon in
our car's air conditioner with any other coolant unless the two
gases behave similarly in the pressure - temperature ranges of
the mechanical device, i.e., they must have the same sign of m
at the pressures the equipment is capable of producing.
 Generally, to use a more environmentally friendly coolant, we
need to replace the old equipment with new equipment that
will operate in the temperature range needed to make m
positive
 The sign of the Joule–Thomson coefficient, μ, depends on the
conditions
 The temperature corresponding to the boundary at a given
pressure is the ‘inversion temperature’ of the gas at that
pressure

12. Application Of throttling
process
 The throttling process is commonly used for the
following purposes :
1. For determining the condition of steam (dryness
fraction)
2. For controlling the speed of the turbine
3. Used in refrigeration plants
4. Liquefaction of gases.
5. In the Linde technique as a standard process in
the petrochemical industry
6. In many cryogenic applications.

13. Liquefaction

14. Simple refrigeration cycle

15. Natural Gas Liquefaction process

16. Hampson-Linde process

17. Controlling the speed of turbine by
throttling

19. References
1. Beattie, J. A. and Bridgeman, O. C., J. Amer. Chem.
Soc., 49, 1665 (1927).
2. Taylor, H. S. and Glasstone, S. (eds.), "A Treatise on
Physical Chemistry", vol. II, 187 ff. van Nostrand,
Princeton, N.J. (1951).
3. Atkins, P.W. "Physical Chemistry", 5th ed., (Freeman,
1994), pp 104-108.
4. “A Textbook of Chemical Engineering
Thermodynamics.” K.V. Narayanan PHI Learning, 6th
ed., pp 127,150, 214.
5. J.H. Noggle, "Physical Chemistry", 3rd ed., Harper
Collins, 1996 pp 104ff.
6. R.G. Mortimer "Physical Chemistry",
Benjamin/Cummings, Redwood City, Calif., 1993, pp
70-73.