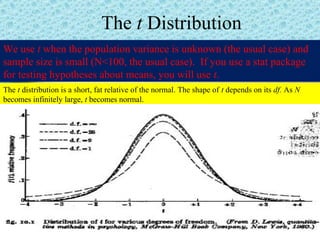
The document discusses the t-test, which is used to test hypotheses about population means when the population variance is unknown. It describes the different types of t-tests (single sample, independent samples, and dependent samples t-tests), the assumptions of the t-test, and provides examples of how to perform single sample and independent samples t-tests. The key points are that the t-test is similar to the z-test but uses the t-distribution instead of the normal due to unknown variances, and the degrees of freedom are related to sample size.

1. The t-test
Inferences about Population Means
SUBMITTED TO:
Dr. Deepali Jat
Associate professor
Dr. H.S. Gour Central University,
Sagar -470003 (M.P.)
SUBMITTED BY: NAGENDRA
SAHU
Dr. H.S. Gour Central University
Sagar-470003 (M.P.)

2. TABLE OF CONTENTS
1. OBJECTIVE
2. BACKGROUND
3. Z-TEST
4. DISTRIBUTION OF t-TEST
5. DEGREE OF FREEDOM
6. SINGLE t-TEST
7. ASSUMPTIONS
8. REFERENCES
9. AKNOWELDGEMENT

3. Questions
• What is the main use of the t-test?
• How is the distribution of t related to the unit normal?
• When would we use a t-test instead of a z-test? Why might
we prefer one to the other?
• What are the chief varieties or forms of the t-test?
• What is the standard error of the difference between means?
What are the factors that influence its size?

4. Background
• The t-test is used to test hypotheses about means
when the population variance is unknown (the usual
case). Closely related to z, the unit normal.
• Developed by Gossett for the quality control of beer.
• Comes in 3 varieties:
• Single sample, independent samples, and dependent

5. What kind of t is it?
• Single sample t – we have only 1 group; want to test against a
hypothetical mean.
• Independent samples t – we have 2 means, 2 groups; no
relation between groups, e.g., people randomly assigned to a
single group.
• Dependent t – we have two means. Either same people in both
groups, or people are related, e.g., husband-wife, left hand-right

6. Single-sample z test
• For large samples (N>100) can use z to test
hypotheses about means.
• Suppose
• Then
• If
M
M
est
X
z
σ
µ
.
)( −
=
N
N
XX
N
s
est X
M
1
)(
.
2
−
−
==
∑
σ
200;5;10:;10: 10 ==≠= NsHH Xµµ
35.
14.14
5
200
5
. ====
N
s
est X
Mσ
05.96.183.2;83.2
35.
)1011(
11 <∴>=
−
=→= pzX

7. The t Distribution
We use t when the population variance is unknown (the usual case) and
sample size is small (N<100, the usual case). If you use a stat package
for testing hypotheses about means, you will use t.
The t distribution is a short, fat relative of the normal. The shape of t depends on its df. As N
becomes infinitely large, t becomes normal.

8. Degrees of Freedom
For the t distribution, degrees of freedom are always a simple
function of the sample size, e.g., (N-1).
One way of explaining df is that if we know the total or mean,
and all but one score, the last (N-1) score is not free to vary. It
is fixed by the other scores. 4+3+2+X = 10. X=1.

9. Single-sample t-test
With a small sample size, we compute the same numbers
as we did for z, but we compare them to the t distribution
instead of the z distribution.
25;5;10:;10: 10 ==≠= NsHH Xµµ
1
25
5
. ===
N
s
est X
Mσ 1
1
)1011(
11 =
−
=→= tX
064.2)24,05(. =t 1<2.064, n.s.
Interval =
]064.13,936.8[)1(064.211
ˆ
=±
± MtX σ
Interval is about 9 to 13 and contains 10, so n.s.
(c.f. z=1.96)

10. Assumptions
• The t-test is based on assumptions of normality and
homogeneity of variance.
• You can test for both these (make sure you learn the
SAS methods).
• As long as the samples in each group are large and
nearly equal, the t-test is robust, that is, still good,