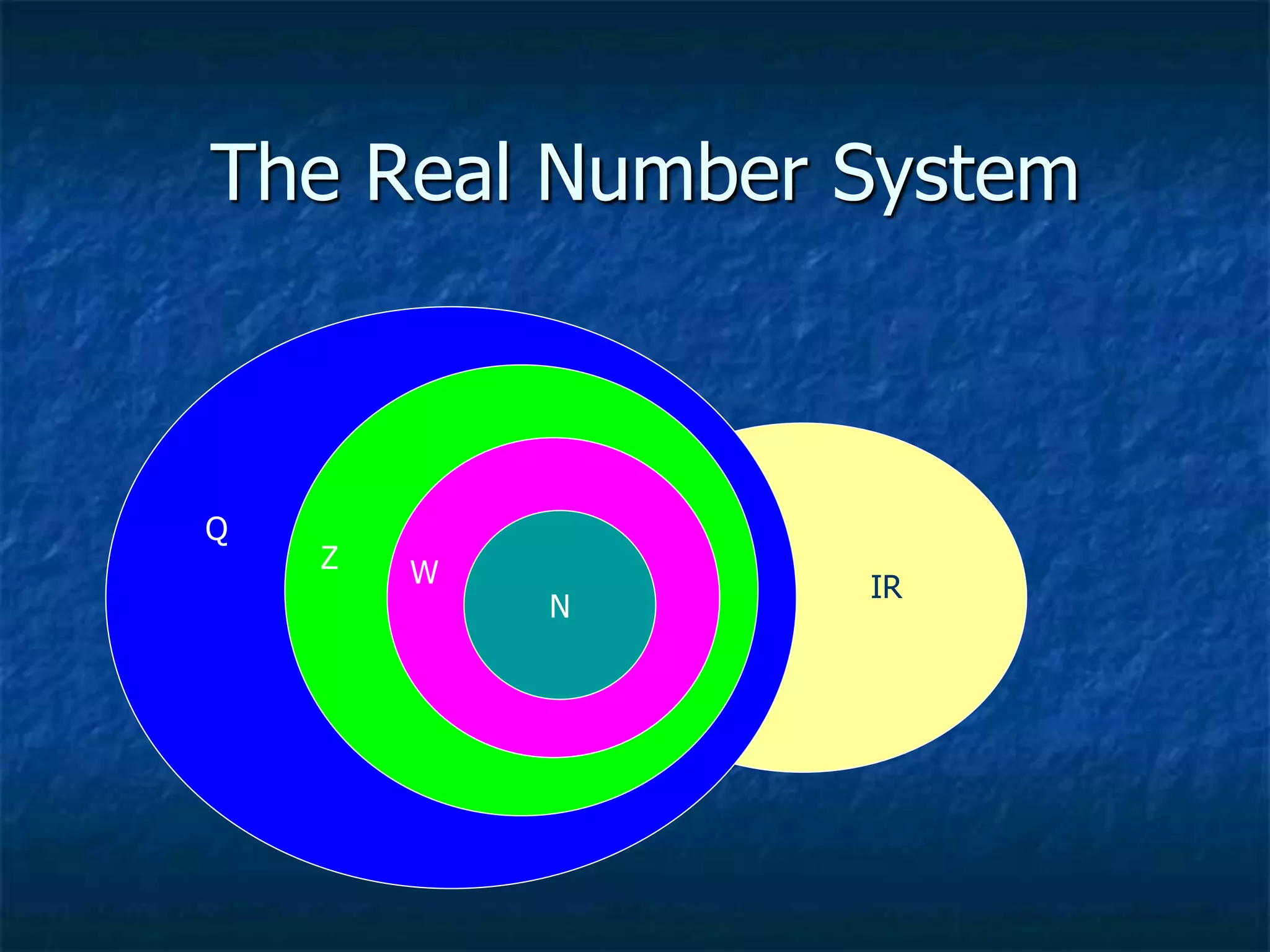
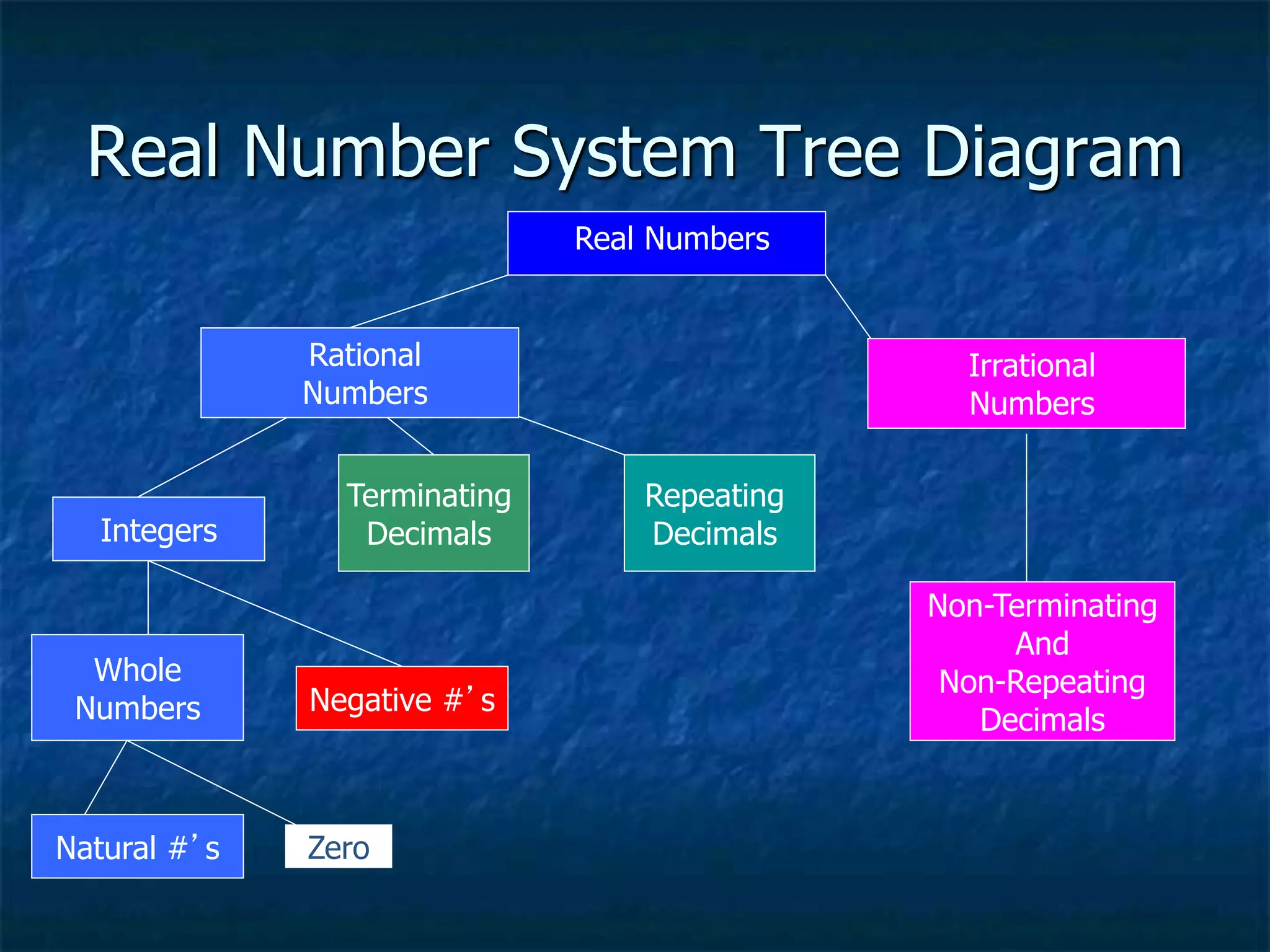
The real number system is composed of both rational and irrational numbers, encompassing five subsets: rational numbers, integers, whole numbers, natural numbers, and irrational numbers. Rational numbers can be expressed as fractions or terminating/repeating decimals, while irrational numbers include non-terminating and non-repeating decimals, like pi. The document also includes examples and exercises to distinguish between different types of numbers.

1. N
W
Z
Q
IR
The Real Number System

2. The Real Number System
 The Real Number System is made up of
a set of rational and irrational numbers.
 It has at five subsets:
1. Rational Numbers (Q)
2. Integers (Z)
3. Whole Numbers (W)
4. Natural Numbers (N)
5. Irrational Numbers (IR)

3. Real Numbers Definitions
 Real Numbers – consists of all rational
and irrational numbers.
 It includes any number that can be written as
a fraction, mixed numbers, terminating and
repeating decimals, whole numbers, integers.
1
2
3
5
4
1.5
2.3333
O
2


4. Rational Numbers
 Rational Numbers – consists of integers,
terminating, and repeating decimals.
 It can also be expressed as a fraction.
1
.5
2
 .9
7.5
{…-3, -2, -1, 0, 1, 2, 3, …}
16 4

5
8 8.83333
6


5. Rational Numbers
 Integers – consist of natural numbers,
their opposites (negative #’s), and zero.
 It does not include fractions or decimals.
 All whole numbers are integers.
 For example:
{…-3, -2, -1, 0, 1, 2, 3, …}

6. Integers
 Whole numbers – consist of natural
numbers and zero. {0, 1, 2, 3, 4,…}
 Natural numbers – are all the counting
numbers. {1, 2, 3, 4…}
 Negative numbers ={…-4, -3, -2, -1}

7. Rational Numbers
 Terminating Decimals are rational
numbers that stops before or after the
decimal point.
 For example: 5.0, 2.75, .40, .0001…etc.
 Repeating Decimals are rational numbers
that repeats after the decimal point.
 For example: .3333…, ,
.75 10.635

8. Irrational Numbers
 Irrational numbers consist of numbers that
are non-terminating and non-repeating
decimals.
 They cannot be express as a fraction!
 Pi is an great example of an irrational number
 http://www.joyofpi.com/pi.html
pi
 
.001, .0011, .00111, .001111…etc
47 4.25837547984...
2

9. Real Number System Tree Diagram
Real Numbers
Integers
Terminating
Decimals
Repeating
Decimals
Whole
Numbers
Rational
Numbers
Irrational
Numbers
Negative #’s
Natural #’s Zero
Non-Terminating
And
Non-Repeating
Decimals

10. Your Turn
1. How are the natural and whole numbers different?
2. How are the integers and rational numbers different?
3. How are the integers and rational numbers the same?
4. How are integers and whole numbers the same?
5. Can a number be both rational and irrational? Use the
diagram to explain your answer.

11. Your Turn
Answer True or False to the statements below. If the statement is
False, explain why.
6. −5 is a rational number. _______
7. is rational. _______
8. is a natural number __________
9. is an integer. _______
10. 2.434434443… is a rational number.____________
16
3.25

8

12. Summary
 What did you learn in this lesson?
 What are some important facts to
remember about the real number system?
 Is there something within the lesson that
you need help on?