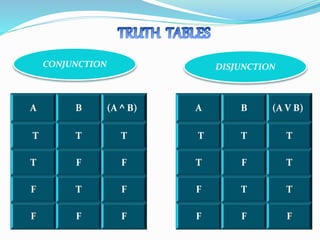
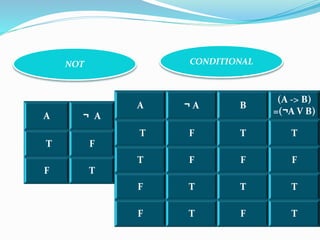
The document discusses propositional and predicate calculus as frameworks for representing mathematical discourse through formulas constructed using logical connectives. It defines various logical operations such as conjunction, disjunction, and negation, along with examples illustrating their application. The concepts of validity and satisfiability of formulas are also introduced, emphasizing the relationship between valid and satisfiable formulas.

2.  PROPOSITIONAL
CALCULUS
 PREDICATE
CALCULUS
 Designed for representing discourse of mathematics.
 Both are simple CFG.
 Strings in both are known as Formulas

3. SYNTAX OF PROPOSITIONAL CALCULUS
Strings are known as Formulas.
A formula is constructed with the aid of Logical Connectives such
as AND,OR, NOT denoted by the symbols ^,v,¬

4. • The word blueberry has
two consecutive r’s
OR
• The word peach has six
letters
 A : the word blueberry
has two consecutive r’s
 B :the word peach has
six letter
(A V B)

5.  A : Stands for the word
“ watermelon has nine
letters,”
 B : Stands for the word
“ blueberry has two
consecutive r’s , “
 C : Stands for the word
“peach has six letters “
 (A ^(B v ¬C)

6.  “ Either Jim or John is
here , but not both “
 Jim is here or John is here
AND
 John is not here or Jim is
not here
((A V B) ^ (¬A V ¬B))
 Jim is here or John is
here;
AND
 It is not the case that Jim
is here AND John is here
((A V B) ^ ¬ (A ^ B))

7. DEFINITION
 The formulas of the propositinal calculus are the
strings generated by the following CFG
G = (V,∑,R,S)
V = ∑ U {S,N}
∑ = { A,I,S,V,^,¬(,)}
R = { N ->e
N ->NI
S ->AN$
S ->(S V S)
S ->(S ^ S)
S -> ¬S }

8. If F and G are any two formula
o ( F ^ G ) :- Conjunction of F and G
o ( F v G ) :- Disjunction of F and G
o ¬ F :- Negation of F
o ( F -> G) :- If F then G
( F -> G) = ( ¬F V G )
(F <-> G) = ( (F->G) ^ (G -> F) )

9. A B (A V B)
T T T
T F T
F T T
F F F
DISJUNCTIONCONJUNCTION
A B (A ˄ B)
T T T
T F F
F T F
F F F

10. NOT
A ¬ A
T F
F T
CONDITIONAL
A ¬ A B
(A -> B)
=(¬A V B)
T F T T
T F F F
F T T T
F T F T

11. VALIDITY & SATISFIABILITY
VALIDITY
 F is valid , if every truth
assignment appropriate to
F verifies.
 i.e , F is a Tautology
SATISFIABILITY &
UNSATISFIABILITY
 SATISFIABLE :- If the truth
table for the formulas
contains atleast one T’s.
 UNSATISFIABLE :- If the
truth table for the formulas
contains all False.
“ EVERY VALID FORMULA IS SATISFIABLE. BUT EVERY
SATISFIABLE FORMULA IS NOT VALID ”

12. THANK YOU