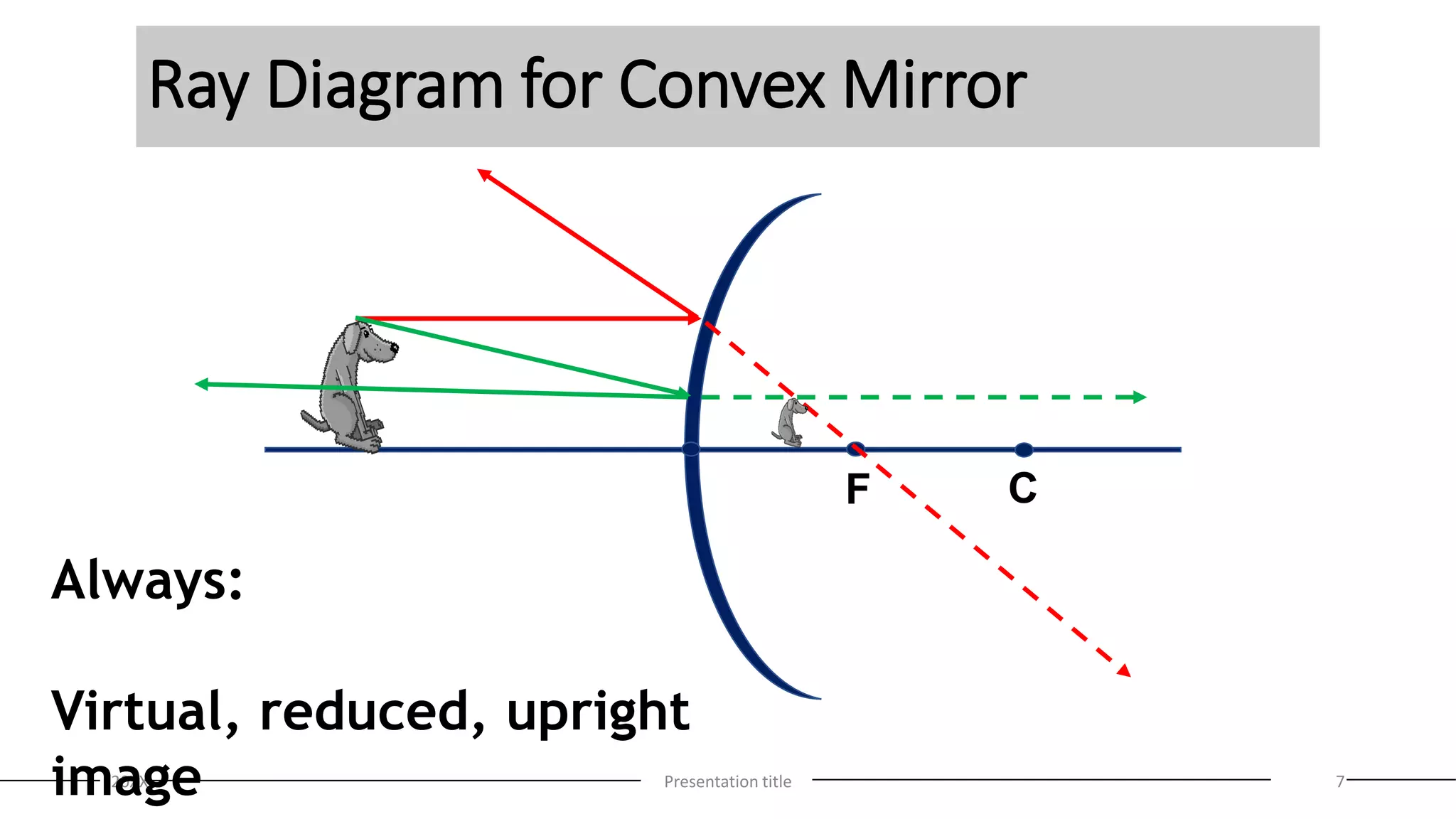
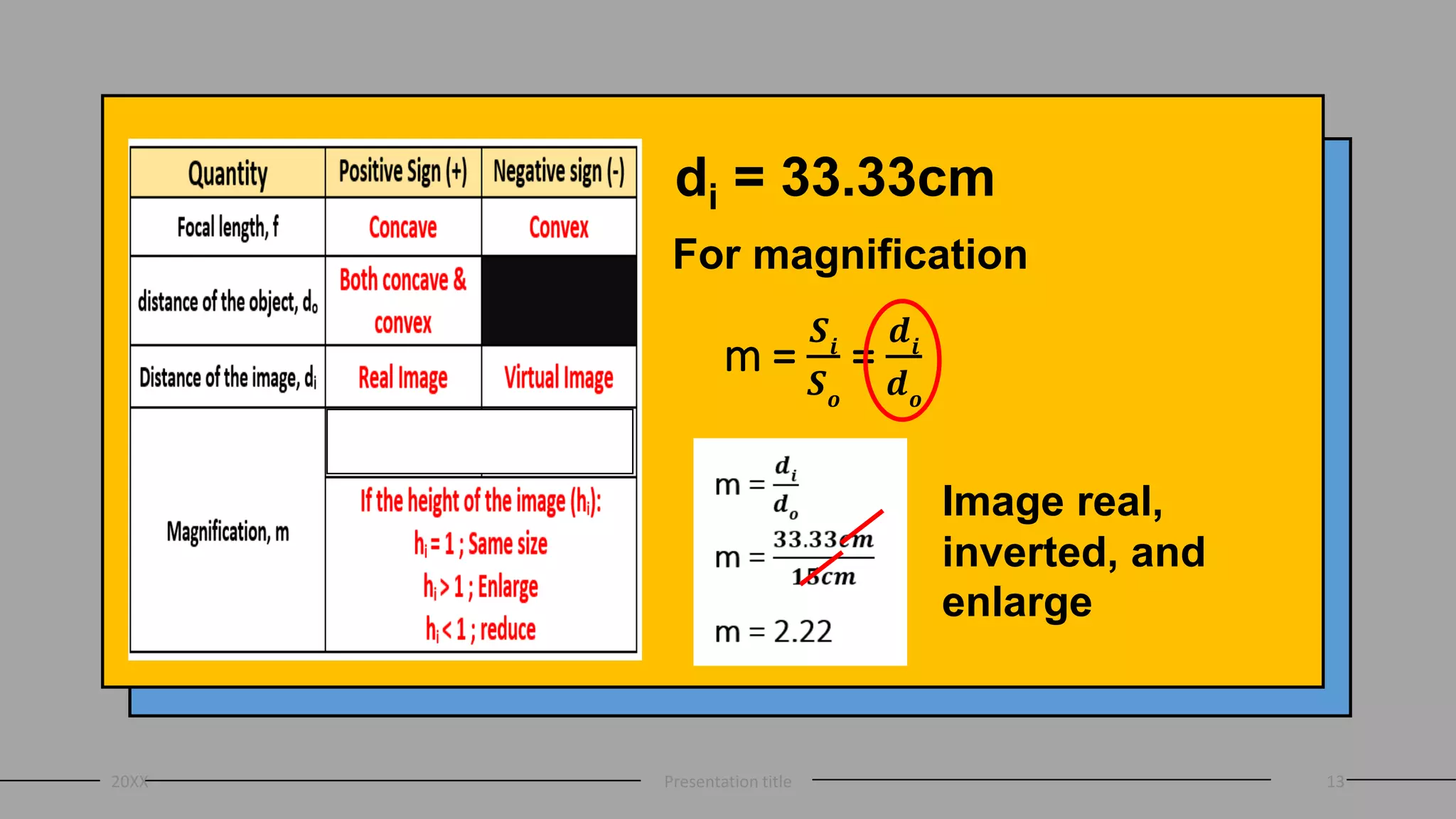
This document discusses curved mirrors and the mirror equation. It defines key terms like focal length, radius of curvature, focal point, vertex, and center of curvature. It explains that the focal length is equal to half the radius of curvature. The location and type of image formed by a concave mirror depends on where the object is placed relative to the center of curvature and focal point. The mirror equation relates the focal length, distance of the object, and distance of the image. Two sample problems demonstrate how to use the mirror equation to calculate the location of an image given information about the focal length and object distance.

1. The Mirror
Equation
@ ATDC

2. Review
2
Identify the parts of a curved mirror.
Principal Axis
Center of
Curvature (C)
Focal Point/
Focus (F)
Vertex (A)
Radius of
Curvature (R)
Focal Length (f)

3. Review
3
Always remember that the focal length
(f) is ½ of the radius of curvature (R)
Radius of
Curvature (R)
Focal Length (f)
f = ½R
For example: if the radius of curvature
is 40cm then the focal length (f) is
20cm.
f = ½ (40cm) =
20cm

4. Summary for Concave Mirror
20XX Presentation title 4
When an object is:
• Beyond C
• At C
• Between C and F
• At F
• Between F and mirror
Image is:
• Between C and F
• At C
• Beyond C
• No image
• Virtual image

5. Convex Mirror
20XX Presentation title 5

6. Ray Diagram for Convex Mirror
20XX Presentation title 6

7. Ray Diagram for Convex Mirror
20XX Presentation title 7
C
F
Always:
Virtual, reduced, upright
image

8. There is an important relationship between the
distance of the object (do), the distance of the
image (di), and the focal length (f). This relationship
is known as the mirror equation.
The mirror equation is an accurate way to find and
describe the image formed by a spherical mirror
through computation or via a mathematical method.
20XX Presentation title 8
The Mirror
Equation

9. This relationship can be expressed using the
equation;
20XX Presentation title 9
The Mirror
Equation
𝟏
𝒇
=
𝟏
𝒅𝒐
+
𝟏
𝒅𝒊
where:
f = focal length
do = distance of the object
Di = distance of the image

10. The mirror equation is applicable to both concave and
convex mirrors. Given the following conditions:
20XX Presentation title 10
The Mirror
Equation

11. m =
𝑺𝒊
𝑺𝒐
=
𝒅𝒊
𝒅𝒐
20XX Presentation title 11
The Mirror
Equation
The formula for magnification can be expressed using
the formula:
Where:
Si = Size of the image sometimes express as hi (Height of the image)
So = Size of the image sometimes express as ho (Height of the object)

12. Sample problem 1
A flower vase is placed 15cm in front of a concave mirror whose focal length is
10cm. Where is the image located? Describe the image.
Given: do = 15cm
f = 10cm
Unknown: di = ?
Formula:
𝟏
𝒇
=
𝟏
𝒅𝒐
+
𝟏
𝒅𝒊
Solution: (you may directly solve
the problem by substituting the
value of the given or you may
derive first the formula)
Answer: di = 33.33cm
Substitute the value in the
given formula then compute
Transposition (Note the sign)
Compute for the value
Cross multiply
Divide both sides to proceed
with the cancellation
Compute

13. 20XX Presentation title 13
di = 33.33cm
m =
𝑺𝒊
𝑺𝒐
=
𝒅𝒊
𝒅𝒐
For magnification
Image real,
inverted, and
enlarge

14. 20XX Presentation title 14
Sample problem 2
A bottle is held 5.0cm from a concave mirror whose
radius is 28.0cm. At what distance will the image be
formed?
Sample problem 3
A cup is placed in front of a curved mirror whose focal
point is at 8cm, and formed an image 24cm beyond C.
At what point thus the cup is located?