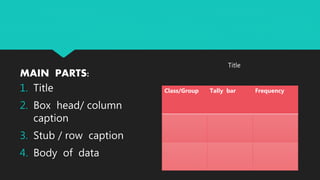
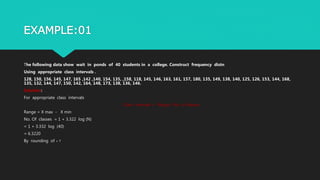
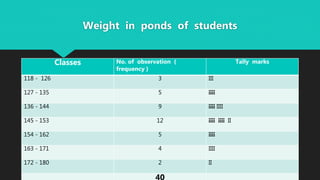
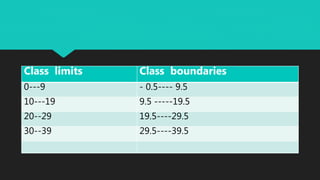
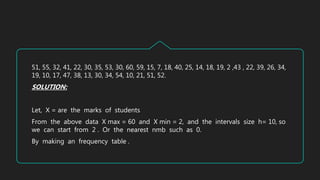
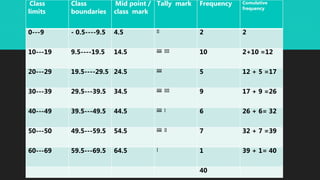
The document defines basic statistics and discusses frequency distribution and types of frequency distributions. It provides steps to construct discrete and continuous frequency distributions, including determining class limits and boundaries. Examples are given to demonstrate creating frequency tables from raw data for discrete and continuous variables. Key concepts discussed include tally marks, frequencies, class intervals, midpoints, and cumulative frequencies.

2. Presented By:
Mahrukh
Shehzadi
Basic Statics

4. BASIC
STATISTICS
DEFINITION:
It is the study of data, descrbing
the property of data and
drawing conclusion about the
population based on information
in a sample.

5. LEARNING OUTCOMES:
Students will able to learned about :
 Construction of Frequency table .
 Construction of Histogram.
 Construction of Frequency polygon.
 Commulative frequency distribution.
 Commutation of Arithmatic mean.
 Properties of Arithmatic mean.

6.  Medin
 Mode
 Geometric mean
 Harmonic mean
 Qurtiles
 Measure of dispersion

7. FREQUENCY DISTRIBUTION
DEFINITION:
It is the arrangement of data in the form of table in such a way
that each class or group showing no. Of observations falling in that class or group is
called a distribution.
GROUPED DATA:
The data presented in the form of frequency distribution is called
grouped data.

9. MAIN PARTS:
1. Title
2. Box head/ column
caption
3. Stub / row caption
4. Body of data
Title
Class/Group Tally bar Frequency

10. TYPES
On the basis of variable or data frequency distribution having
Two types .
1. Discrete frequency distribution
2. Countinuous frequency distribution

11. DISCRETE FREQUENCY DISTRIBUTION
Following steps are involved for the construction of descrete frequency table.
1. First of all we should need to find the minimum and maximum observation in data and
write the value in variable column from minimum to maximum.
2. Record the observation by using Vertical bar(|) called “ tally mark’’.
3. Count the tally and write down the frequency in frequency column.

12. Example (01)
Five coins are tossed 20 times and the number of heads recorded at each toss are
given below;3,4,2,3,3,5,2,2,2,1,1,2,1,4,2,2,3,3,4,2
Make frequency distribution of the number of heads observed
Solution;
Let X= Number of heads. The frequency distribution is given below
X Tally marks Frequency
1 III 3
2 IIII III 8
3 IIII 5
4 III 3
5 I 1

13. EXAMPLE (02)
The following is the number of female
employees in different braches of
commercial banks. Make a frequency
distribution.
2,4,6,1,3,5,3,7,8,6,4,7,4,4,2,1,3,6,4,2,5,7,9,1,2,10,1,
8,9,2,3,1,2,3,4,4,4,6,6,5,5,4,5,8,5,4,3,3,2,5,0,5,9
,9,8,10,0,4,10,10,1,1,2,2,1,8,6,9,10
The minimum value = 0
The maximum value=10
The number of frequency employees
X Tally marks Frequency
0 II 2
1 IIII III 8
2 IIII IIII 9
3 IIII II 7
4 IIII IIII I 11
5 IIII III 8
6 IIII I 6
7 III 3
8 IIII 5
9 IIII 5
10 IIII 5

14. CONTINUOUS FREQUENCY TABLE
 I - Find the Range, where Range = Xmax - Xmin (the difference between maximum and minimum observations).
II – Decide about the number of groups (denote it by k)into which
the data is to be classified (usually an integer between 5 and
20).usually it depends upon the range .The larger the range the
more the number of groups.
III – Determine the size of the class (denote by h)by using the
formula;
h= range/k (use formula when b is not given)

15. NOTE; The rule of approximation is relaxed in determining h . For example h = 7.1 or h = 7.9 may be
taken as 8.
 IV- Start writing the classes or group of the frequencies distribution usually starting from the
minimum observation and keeping in view the size of the class.
 V- Record the observation from the data by using tally marks .
 VI- Count the number of tally marks and record them in the frequency column for each class.

16. EXAMPLE:01
The following data show wait in ponds of 40 students in a college. Construct frequency distn
Using appropriate class intervals .
128, 150, 156, 145, 147, 165 ,142 ,140, 154, 135, ,158, 118, 145, 146, 163, 161, 157, 180, 135, 149, 138, 140, 125, 126, 153, 144, 168,
135, 132, 144, 147, 150, 142, 164, 148, 173, 138, 136, 146.
Solution:
For appropriate class intervals
Class intervals = Range / No. of classes
Range = X max - X min
No. Of classes = 1 + 3.322 log (N)
= 1 + 3.332 log (40)
= 6.3220
By rounding of = 7

17. Weight in ponds of students
Classes No. of observation (
frequency )
Tally marks
118 - 126 3 III
127 - 135 5 IIII
136 - 144 9 IIII IIII
145 - 153 12 IIII IIII II
154 - 162 5 IIII
163 - 171 4 IIII
172 - 180 2 II
40

18. Concepts of countinuous frequency distribution :
CLASS LIMITS:
These are the minimum and maximum values defined for a class or group .
 The minimum value of a class is called lower class limit.
 The maximum value of a class is called uper class limit.

19. CLASS BOUNDRIES:
A class boundary is obtained by adding two successive class
limits and dividing the sum by 2. The value so obtained is taken
as upper class boundary for the previous class and lower
class boundary for the next class.

20. Class limits Class boundaries
0---9 - 0.5---- 9.5
10---19 9.5 -----19.5
20--29 19.5----29.5
30--39 29.5----39.5

21. By looking the previous table we can say that the real lower class limit of 10 is 9.5, is all
values between 9.5 and 10.49 are considered as 10. While the upper class limit is 19.5 as all
value between 18.5 and 19.5 are recorded as 19. So the real class limit of a class is called
class boundary.
MID POINT OR CLASS MARK:
For a given class the average of that class obtained by dividing the sum of upper and lower
class limits by 2. Is called midpoint or class mark of that class.

22. COMULATIVE FREQUENCY:
The total frequency upto an upper class limit or boundary is called
Comulative frequency.
The previous concept can be explained by an Example.
EXAMPLE:
The following are the marks obtained by 40 students of maths class in class X. Make frequency
distribution with a class interval of 10.

23. 51, 55, 32, 41, 22, 30, 35, 53, 30, 60, 59, 15, 7, 18, 40, 25, 14, 18, 19, 2 ,43 , 22, 39, 26, 34,
19, 10, 17, 47, 38, 13, 30, 34, 54, 10, 21, 51, 52.
SOLUTION:
Let, X = are the marks of students
From the above data X max = 60 and X min = 2, and the intervals size h= 10, so
we can start from 2 . Or the nearest nmb such as 0.
By making an frequency table .

24. Class
limits
Class
boundaries
Mid point /
class mark
Tally mark Frequency Comulative
frequency
0---9 - 0.5----9.5 4.5 II 2 2
10---19 9.5----19.5 14.5 IIII IIII 10 2+10 =12
20---29 19.5----29.5 24.5 IIII 5 12 + 5 =17
30---39 29.5---39.5 34.5 IIII IIII 9 17 + 9 =26
40---49 39.5---49.5 44.5 IIII I 6 26 + 6= 32
50---50 49.5---59.5 54.5 IIII II 7 32 + 7 =39
60---69 59.5---69.5 64.5 I 1 39 + 1= 40
40