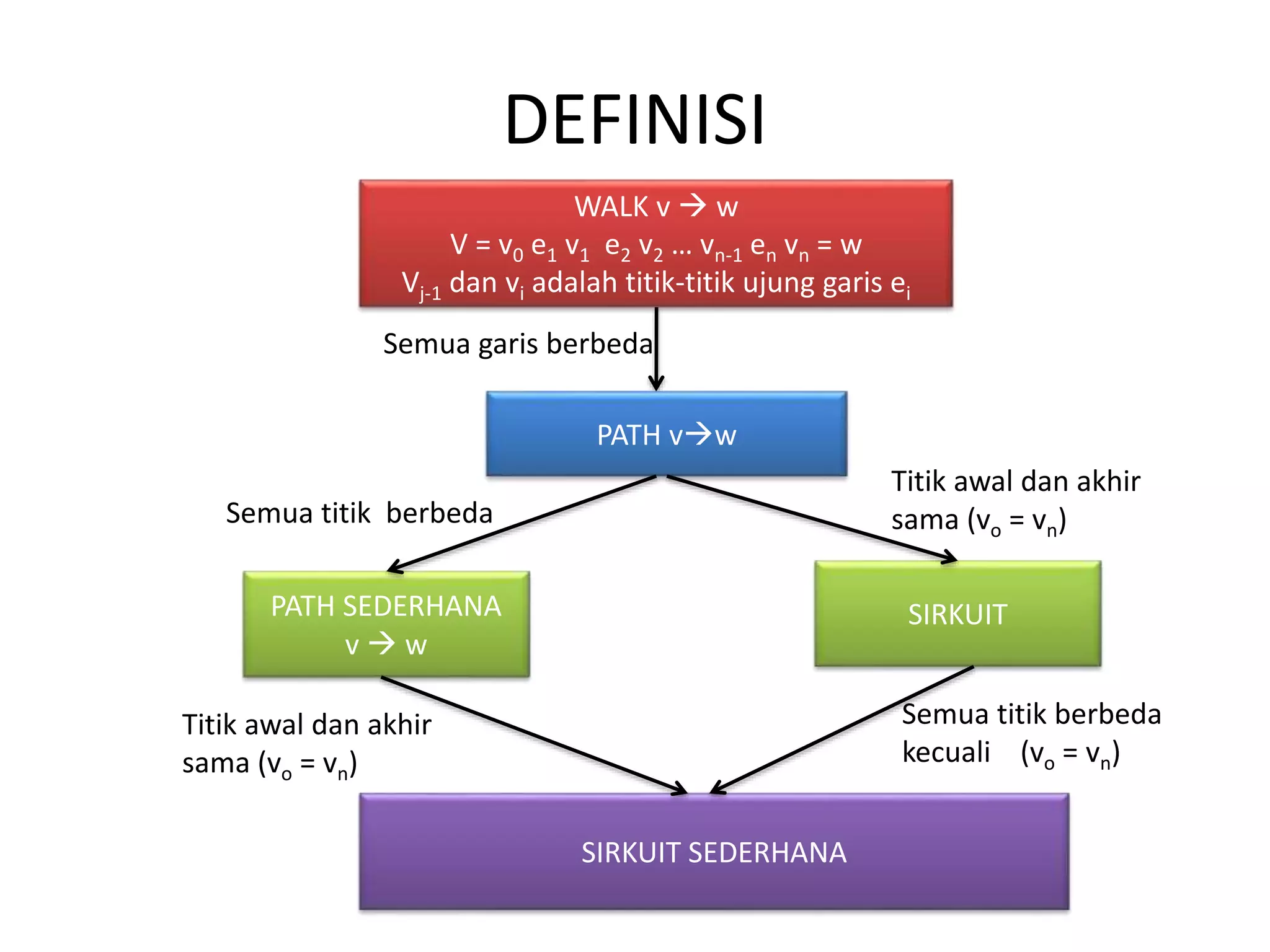
Dokumen ini membahas tentang teori graf, yaitu: 1. Walk adalah barisan titik dan garis secara berselang-seling dalam graf yang dimulai dan diakhiri oleh dua titik. 2. Path adalah walk dimana semua garisnya berbeda. 3. Sirkuit adalah path dimana titik awal dan akhirnya sama.

1. PATH DAN SIRKUIT
TEORI GRAPH
STT WASTUKANCANA
Ismi Kaniawulan

2. WALK
• Misalkan G adalah suatu graf. Misalkan pula v dan
w adalah 2 titik dalam G.
• SuatuWalk dari v ke w adalah barisan titik-titik
berhubungan dan garis secara berselang-seling,
diawali dari titik v dan diakhiri pada titik w.
• Walk dengan panjang n dari v ke w dituliskan
sebagai sebagai berikut v0 e1 v1 e2 v2…..vn-1 en vn
dengan v0 = v ; vn = w; vn = w; vi-1 dan vi adalah
titik-titik ujung garis ei

3. TENTUKAN WALK DARI 1 KE 7
1 ea 2 eb 3 ec 4 ed 5 ee 6 el 7 n=6

4. PATH
• Path dengan panjang n dari v ke w adalah
Walk dari v ke w yang semua garisya berbeda.
Path dari v ke w dituliskan sebagai berikut v =
v0 e1 v1 e2 v2…..vn-1 en vn = w dengan ei <> ej
untuk I <> j dan vk <> vm untuk k<>m

5. PATH SEDERHANA
• Path sederhana dengan panjang n dari v ke w
adalah Path dari v ke w yang semua titiknya
berbeda. Path sedrhana dari v ke w berbentuk
v = v0 e1 v1 e2 v2…..vn-1 en vn = w dengan ei <> ej
untuk I <> j dan vk <> vm untuk k<>m

6. SIRKUIT
• Sirkuit dengan panjang n adalah path yang
dimulai dan diakhiri pada titik yang sama.
Sirkuit adalah path yang berbentuk v0 e1 v1 e2
v2…..vn-1 en vn dengan vo = vn

7. SIRKUIT SEDERHANA
• Sirkuti sedrhana denga panjang n adalh sirkuit
yang semua titiknya berbeda. Sirkuit
sederhana berbentuk v0 e1 v1 e2 v2…..vn-1 en vn
dengan ei <> ej untuk I <> j dan vk <> vm untuk
k<>m kecuali vo = vn

8. DEFINISI
WALK v  w
V = v0 e1 v1 e2 v2 … vn-1 en vn = w
Vj-1 dan vi adalah titik-titik ujung garis ei
Semua garis berbeda
PATH vw
Titik awal dan akhir
sama (vo = vn Semua titik berbeda )
PATH SEDERHANA
v  w
SIRKUIT
SIRKUIT SEDERHANA
Semua titik berbeda
kecuali (vo = vn)
Titik awal dan akhir
sama (vo = vn)

9. Latihan
• Tentukan
• Walk dari v1 ke v8 n = 10
• Path dari v1 ke v6 n = 7
• Path sederhana v1 ke v4
• Sirkuit v3 ke v3
• Sirkuit sederhana dari v1 ke v1

10. Latihan