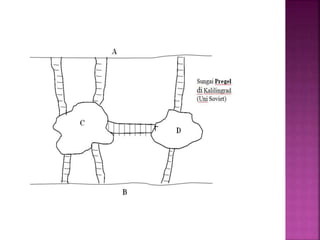
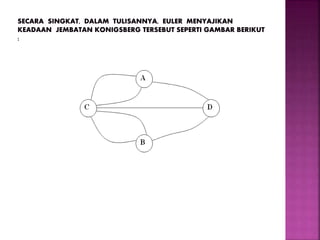
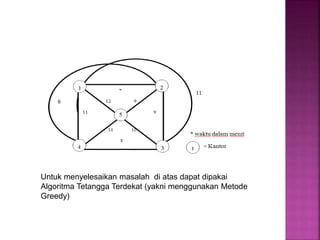
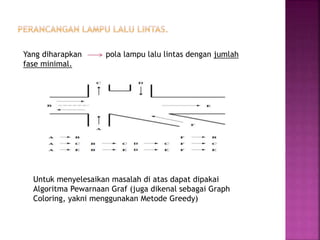
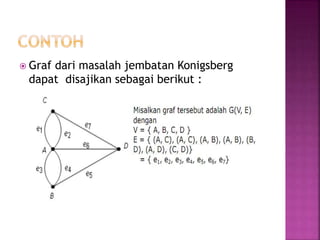
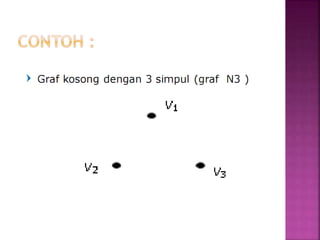
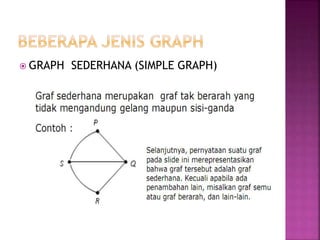
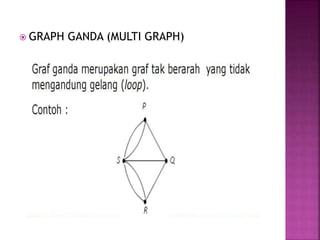
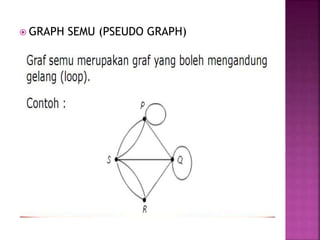
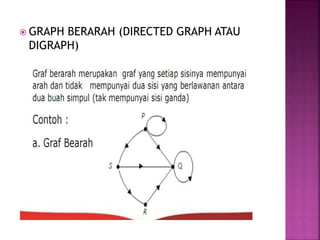
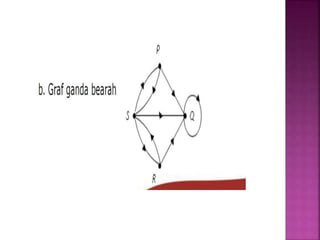
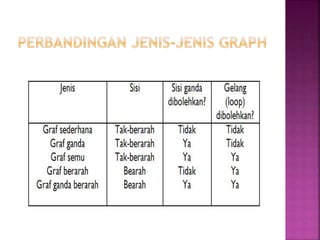
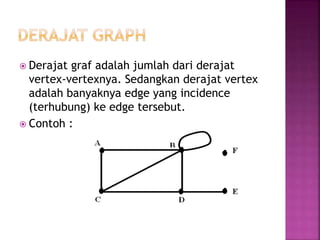
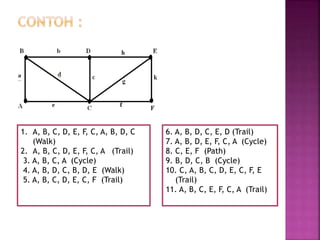
Dokumen tersebut membahas tentang teori graf, yang meliputi konsep dasar graf seperti simpul, sisi, jenis-jenis graf, derajat simpul, walk, trail, path, dan cycle. Dokumen tersebut juga menjelaskan contoh masalah jembatan Konigsberg yang merupakan awal mula teori graf dan langkah-langkah penyelesaian masalah dengan menggunakan graf.

2.  Tujuan :
1. Mahasiswa memahami konsep dan terminologi
graf
2. Mahasiswa memodelkan masalah dalam
bentuk graf
3. Mahasiswa dapat menyelesaikan berbagai
Persoalan yang terkait dengan Teori Graph

3.  Teori Graf mulai dikenal pada saat seorang
matematikawan bangsa Swiss, bernama
Leonhard Euler, berhasil mengungkapkan
Misteri Jembatan Konigsberg pada tahun
1736. Di Kota Konigsberg (sekarang bernama
Kalilingrad, di Uni Soviet) mengalir sebuah
sungai bernama sungai Pregel. Di tengah
sungai tersebut terdapat dua buah pulau.
Dari kedua pulau tersebut terdapat jembatan
yang menghubungi ke tepian sungai dan
diantara kedua pulau. Jumlah jembatan
tersebut adalah 7 buah seperti gambar
berikut :

6.  Dalam masalah di atas, daratan (tepian A dan
B, serta pulau C dan D) disajikan sebagai titik
dan jembatan disajikan sebagai ruas garis.
Euler mengemukakan teoremanya yang
mengatakan bahwa perjalanan yang
diinginkan di atas (yang kemudian dikenal
sebagai perjalanan Euler) akan ada apabila
graf terhubung dan banyaknya garis yang
datang pada setiap titik (derajat simpul)
adalah genap.

7.  Secara umum, langkah-langkah yang perlu
dilalui dalam penyelesaian suatu masalah
dengan bantuan komputer adalah sebagai
berikut :
 Problema Model Yang Tepat Algoritma
Program Komputer

8.  Petugas kantor telepon yang ingin
mengumpulkan koin-koin dari telepon umum.
Berangkat dari kantor & kembali ke
kantornya lagi.
 Yang diharapkan ® suatu rute perjalanan
dengan waktu minimal. Masalah di atas
dikenal sebagai Travelling Salesman Problem

9. Untuk menyelesaikan masalah di atas dapat dipakai
Algoritma Tetangga Terdekat (yakni menggunakan Metode
Greedy)

10. Yang diharapkan pola lampu lalu lintas dengan jumlah
fase minimal.
Untuk menyelesaikan masalah di atas dapat dipakai
Algoritma Pewarnaan Graf (juga dikenal sebagai Graph
Coloring, yakni menggunakan Metode Greedy)

11.  Graf merupakan struktur diskrit yang terdiri
himpunan sejumlah berhingga obyek yang
disebut simpul (vertices, vertex) dan
himpunan sisi (edges) yang menghubungkan
simpul-simpul tersebut. terdiri dari dari Graf
digunakan untuk merepresentasikan objek-
objek diskrit dan hubungan antara objek-
objek tersebut.
 Notasi sebuah graph adalah G= (V,E) dimana :

12. V merupakan himpunan tak
kosong dari simpul-simpul
(vertices), misalkan V = { v1
, v2 , ... , vn }
E merupakan himpunan sisi – sisi
(edges) yang menghubungkan
sepasang simpul, misalkan E =
{e1, e2 , ... , en}


13.  Graf dari masalah jembatan Konigsberg
dapat disajikan sebagai berikut :

14. Pada graf tersebut sisi e1 = (A, C)
dan sisi e2 = (A, C) dinamakan sisi-
ganda (multiple edges atau paralel
edges) karena kedua sisi ini
menghubungi dua buah simpul yang
sama, yaitu simpul A dan simpul C.
Begitu pun dengan sisi e3 dan sisi e4
. Sementara itu, pada graf diatas,
tidak terdapat gelang (loop), yaitu
sisi yang berawal dan berakhir pada
simpul yang sama.

15. Dari definisi graf, himpunan sisi (E)
memungkinkan berupa himpunan
kosong. Jika graf tersebut
mempunyai himpunan sisi yang
merupakan himpunan kosong maka
graf tersebut dinamakan graf kosong
(null graph atau empty graph)

17.  Dengan memperhatikan kondisi sisinya, suatu
graf dapat dikategorikan sebagai graf tidak
berarah dan graf berarah.
 Graf tidak berarah, seperti telah dijelaskan
pada contoh graf untuk jembatan Konigsberg.
 Graf berarah (directed graph, digraph)
merupakan graf yang mempunyai sisi yang
berarah, artinya satu buah simpul yang
dihubungkan oleh sisi tersebut merupakan
simpul awal (initial vertex) dan simpul yang
lain dikatakan sebagai simpul akhir (terminal
vertex)

18.  GRAPH SEDERHANA (SIMPLE GRAPH)

19.  GRAPH GANDA (MULTI GRAPH)

20.  GRAPH SEMU (PSEUDO GRAPH)

21.  GRAPH BERARAH (DIRECTED GRAPH ATAU
DIGRAPH)

24.  Derajat graf adalah jumlah dari derajat
vertex-vertexnya. Sedangkan derajat vertex
adalah banyaknya edge yang incidence
(terhubung) ke edge tersebut.
 Contoh :

25. Berdasarkan derajat vertex, sebuah vertex dapat disebut :
Vertex Ganjil, bila derajat vertexnya merupakan bilangan ganjil
Vertex Genap, bila derajat vertexnya merupakan bilangan genap
Vertex Bergantung / Akhir, bila derajat vertexnya adalah 1
Vertex Terpencil, bila derajat vertexnya adalah 0

26.  Dalam keterhubungan sebuah graf, akan
dikenal beberapa istilah-istilah berikut :
1. Walk : barisan vertex dan edge
2. Trail : Walk dengan edge yang berbeda
3. Path / Jalur : Walk dengan vertex yang
berbeda
4. Cycle / Sirkuit : Trail tertutup dengan
derajat setiap vertex = 2

27. 1. A, B, C, D, E, F, C, A, B, D, C
(Walk)
2. A, B, C, D, E, F, C, A (Trail)
3. A, B, C, A (Cycle)
4. A, B, D, C, B, D, E (Walk)
5. A, B, C, D, E, C, F (Trail)
6. A, B, D, C, E, D (Trail)
7. A, B, D, E, F, C, A (Cycle)
8. C, E, F (Path)
9. B, D, C, B (Cycle)
10. C, A, B, C, D, E, C, F, E
(Trail)
11. A, B, C, E, F, C, A (Trail)