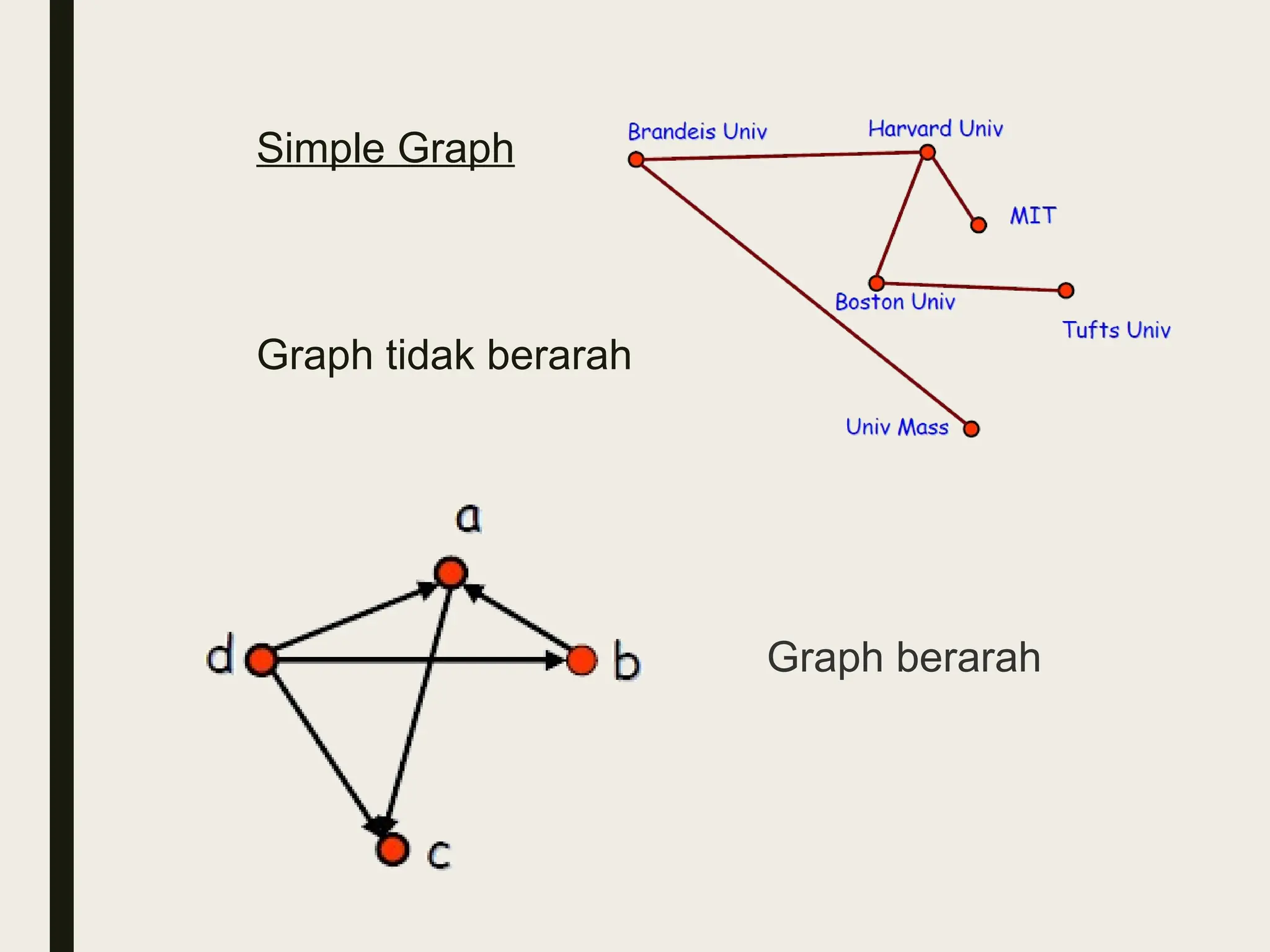
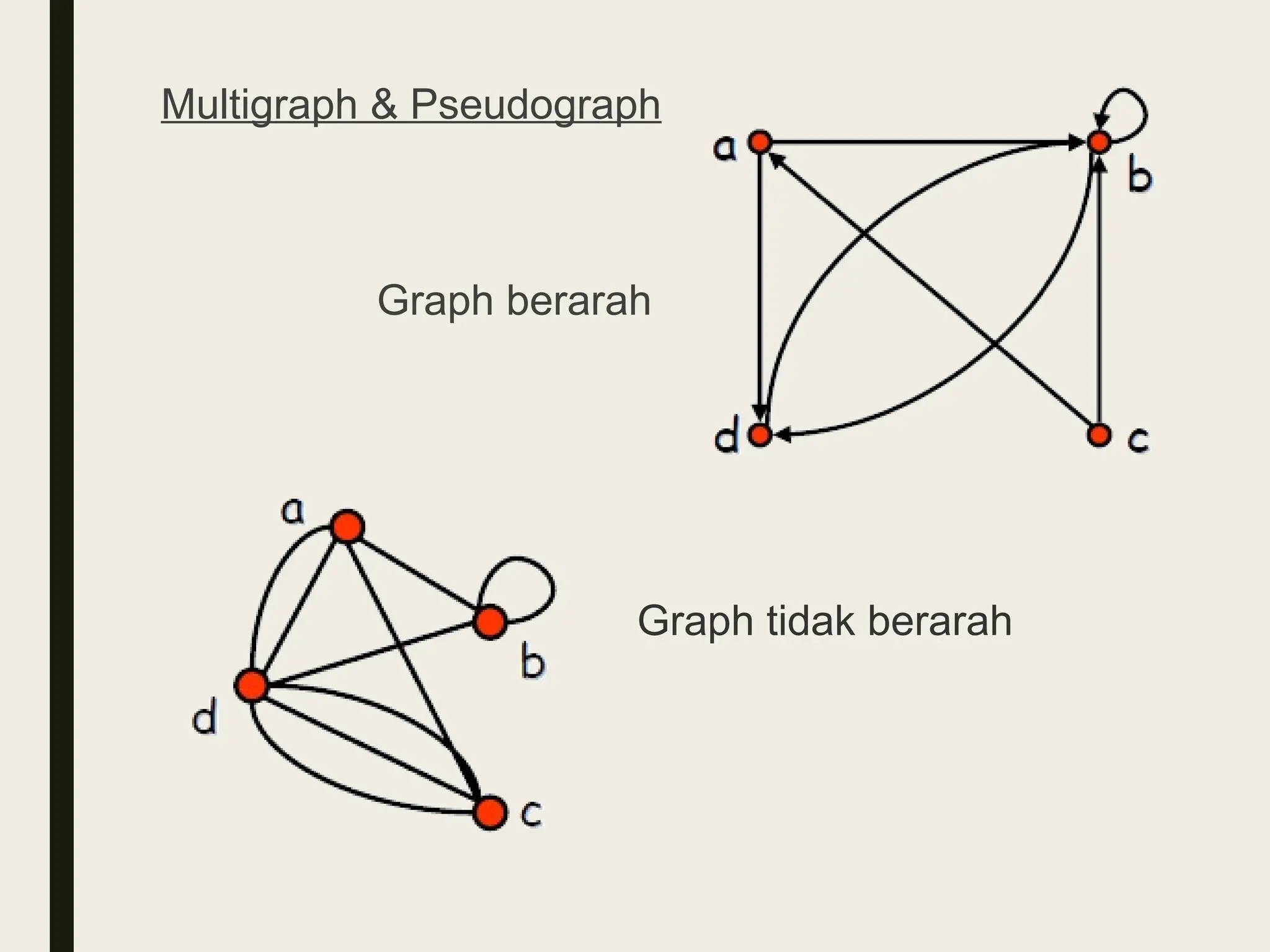
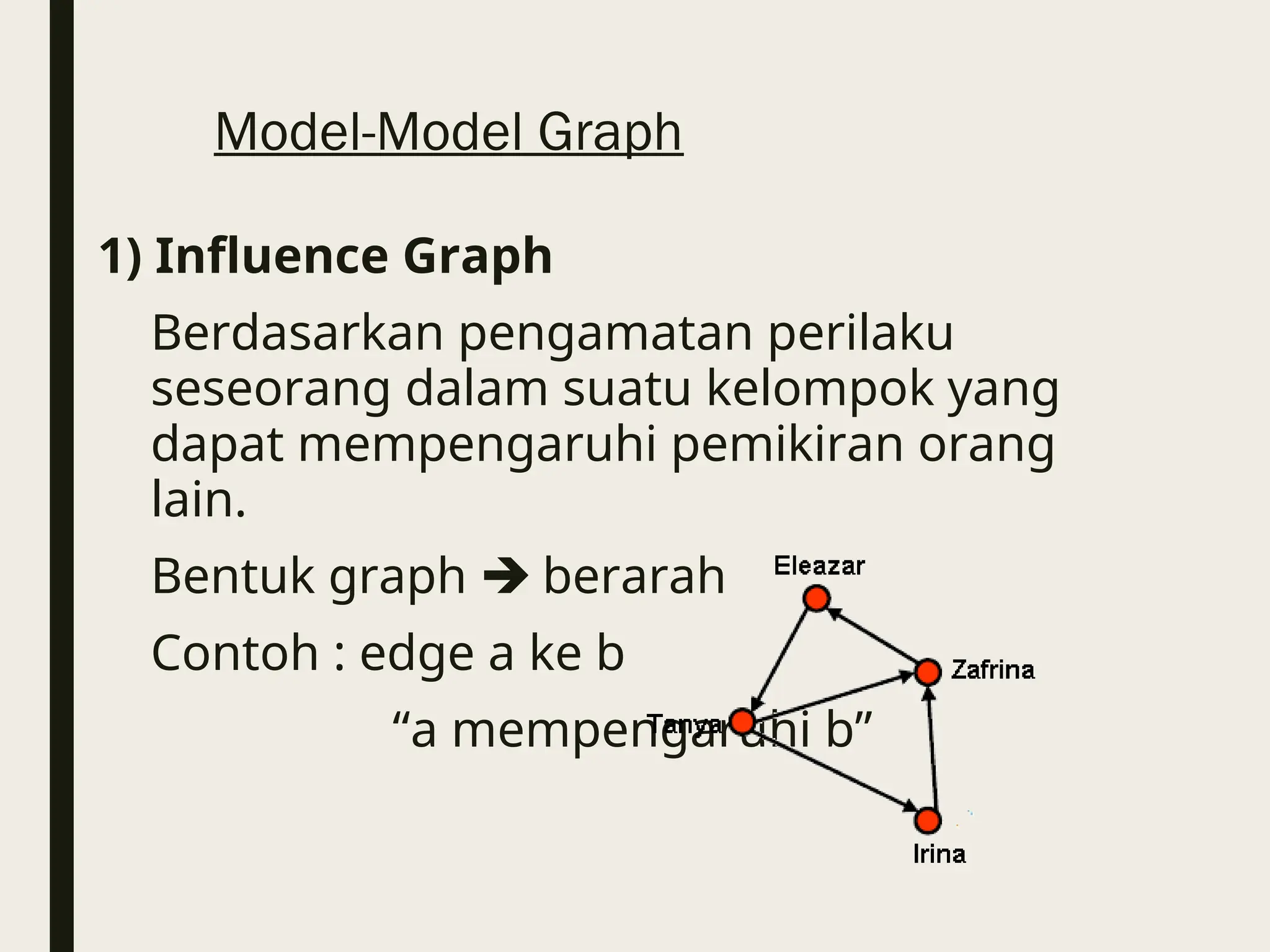
Dokumen ini membahas pengenalan graf dalam matematika diskrit, termasuk definisi, jenis-jenis graf, dan terminologi penting. Hal ini menjelaskan berbagai model graf, operasi graf, serta representasi graf seperti adjacency list dan matrix. Selain itu, dijelaskan juga teorema isomorfisme yang digunakan untuk menentukan kesetaraan antara dua graf.

1. GRAPH
Matematika Diskrit

2. PENGENALAN GRAPH
₪ Suatu diagram yg memuat informasi
tertentu jika diinterpretasikan secara tepat
₪ Digunakan untuk menggambarkan
berbagai macam struktur yg ada.
₪ Tujuannya sebagai visualisasi objek-objek
agar lebih mudah dimengerti
₪ Contoh : Struktur organisasi, bagan alir
pengambilan mata kuliah, peta, rangkaian
jaringan komputer, dsb.

3. DASAR-DASAR GRAPH
Suatu graf sederhana G=(V,E) terdiri dari himpunan
tak kosong dari simpul (vertex) V, dan himpunan
pasangan tak berurut anggota berlainan dari V
yang disebut sebagai garis hubung (edge) E
₪Titik Ujung (End Point) Setiap garis berhubungan
dengan satu atau dua titik.
₪Loop disebut Garis yang hanya berhubungan
dengan satu titik ujung,
₪Garis Parallel disebut Dua garis berbeda yg
menghubungkan titik yg sama,
₪Titik Terasing (Isolating Point) disebut titik yg tidak
mempunyai garis yg berhubungan dengannya,
₪Pendant disebut Titik yg hanya berdegree 1,

4. Jenis-Jenis Graph
1) Graph Sederhana (Simple Graph)
Graph yg memiliki 1 buah edge/garis yang
menghubungkan tiap vertex. Tidak ada loop. Tidak ada
garis parallel.
2) Multigraph
Graph yg memiliki lebih dari 1 edge yg menghubungkan
pasangan vertex yg sama (ada garis parallel)
3) Pseudograph
Graph yg memiliki edge loop
4) Graph Berarah (Directed Graph)
Graph yg semua edgenya memiliki arah
5) Graph Tidak Berarah (Undirected Graph)
Graph yg semua edgenya tidak memiliki arah
6) Multigraph Berarah
7) Multigraph Tidak Berarah

5. Simple Graph
Graph tidak berarah
Graph berarah

6. Multigraph & Pseudograph
Graph berarah
Graph tidak berarah

7. Terminology Graph
1) Terminology pada graph tidak berarah
- Adjacent : saling berhubungan
- Incident / Connect : ada garis yang menghubungkan
antar vertex
- End Points
- Degree : jumlah edge yg berhubungan dengan tiap
vertex deg(v)
- Vertex h dan i adjacent
- Edge e incident dengan vertex h dan i
- Vertex h dan I adalah end point dari edge e
- deg(h) = 1 ; deg(i) = 1

8. 2) Terminology pada graph berarah
- Adjacent : saling berhubungan ‘ke – dari’
- Initial Vertex : vertex awal
- Terminal Vertex : vertex akhir
- Degree :
–In degree  deg-
(v)
–Out degree  deg+
(v)
–a adjacent ke b
–b adjacent dari a
–a initial vertex dari edge d atau edge(a,b)
–b terminal vertex dari edge d atau edge(a,b)
–Degree :
deg-
(a) = 0 ; deg-
(b) = 1
deg+
(a) = 1 ; deg+
(b) = 0

9. Berapakah degree dari graph berikut ini?
1)
2)

10. Teorema Handshaking
Misalkan G = (V, E) suatu graph tak berarah dengan garis
hubung e. Maka :
Teorema ini tetap berlaku meskipun pada graph terdapat
garis hubung ganda maupun loop ganda.
Contoh :
Ada berapa garis hubungkah/edge dalam suatu graph
yang memiliki 6 vertex, yang masing-masing vertexnya
berderajat 10?

11. Model-Model Graph
1) Influence Graph
Berdasarkan pengamatan perilaku
seseorang dalam suatu kelompok yang
dapat mempengaruhi pemikiran orang
lain.
Bentuk graph  berarah
Contoh : edge a ke b
“a mempengaruhi b”

12. 2) Round-Robin Tournament’s
Didasarkan pada sebuah turnamen, setiap tim
bermain dengan tim lain tepat 1 kali.
Tim diwakili dengan vertex
edge dari a ke b: “a mengalahkan b”

13. 3) Graph Khusus
a. Graph Lengkap
Graph lengkap dengan n vertex (simbol Kn) adalah
graph sederhana dengan n vertex, dimana setiap
2 titik berbeda dihubungkan dengan suatu garis
Banyaknya garis dalam suatu graph lengkap
dengan n vertex adalah :

14. b. Graph Siklus (Cycle)  Cn
Graph Siklus (Cycle) Cn, n 3, terdiri atas
≥ n buah
simpul v1, v21, …, vn
c. Graph Roda (Wheel)  Wn
Dihasilkan dari Pemberian satu vertex tambahan
pada suatu siklus Cn, n 3, dan lalu
≥
menghubungkan vertex tersebut ke setiap vertex
pada Cn dengan edge baru.

15. d. Graph Kubus (Cube)  Qn
Kubus-n (n-cube) adalah graph yang vertexnya merepresentasikan
string 2n
bit sepanjang n. Dua vertex terhubung jika dan hanya jika
bit string yang direpresentasikannya berbeda tepat satu bit.
e) Graph Bipartite  Km,n
Suatu graph sederhana G disebut bipartite jika himpunan vertex V-
nya dapat dipartisi menjadi dua himpunan tak kosong yang tak
beririsan V1 dan V2 sedemikian hingga setiap edge dalam graph
menghubungkan suatu vertex di V1 dengan vertex di V2
(sedemikian hingga tak ada edge di dalam G yg menghubungkan
dua vertex di V1 maupun di V2).

16. Contoh :

Bipartite Lengkap : Terhubung sempurna
Bipartite : Terhubung

17. Operasi-Operasi Graph
1) Sub-graph
Suatu subgraph dari graf G = (V, E) adalah graf H = (W, F)
dimana W  V dan F  E.
Contoh :
K5 Subgraph K5

18. 2) Union atau Gabungan
Gabungan dari dua graph sederhana G1 = (V1, E1)
dan G2 = (V2, E2) adalah graph sederhana dengan
himpunan vertex V1 
 V2 dan himpunan garis hubung E1

 E2.
Gabungan dari G1 dan G2 : G1 
 G2.

19. Representasi Graph
1) Adjacency List
Menentukan vertex-vertex yg adjacent dengan
vertex di graph
Contoh :

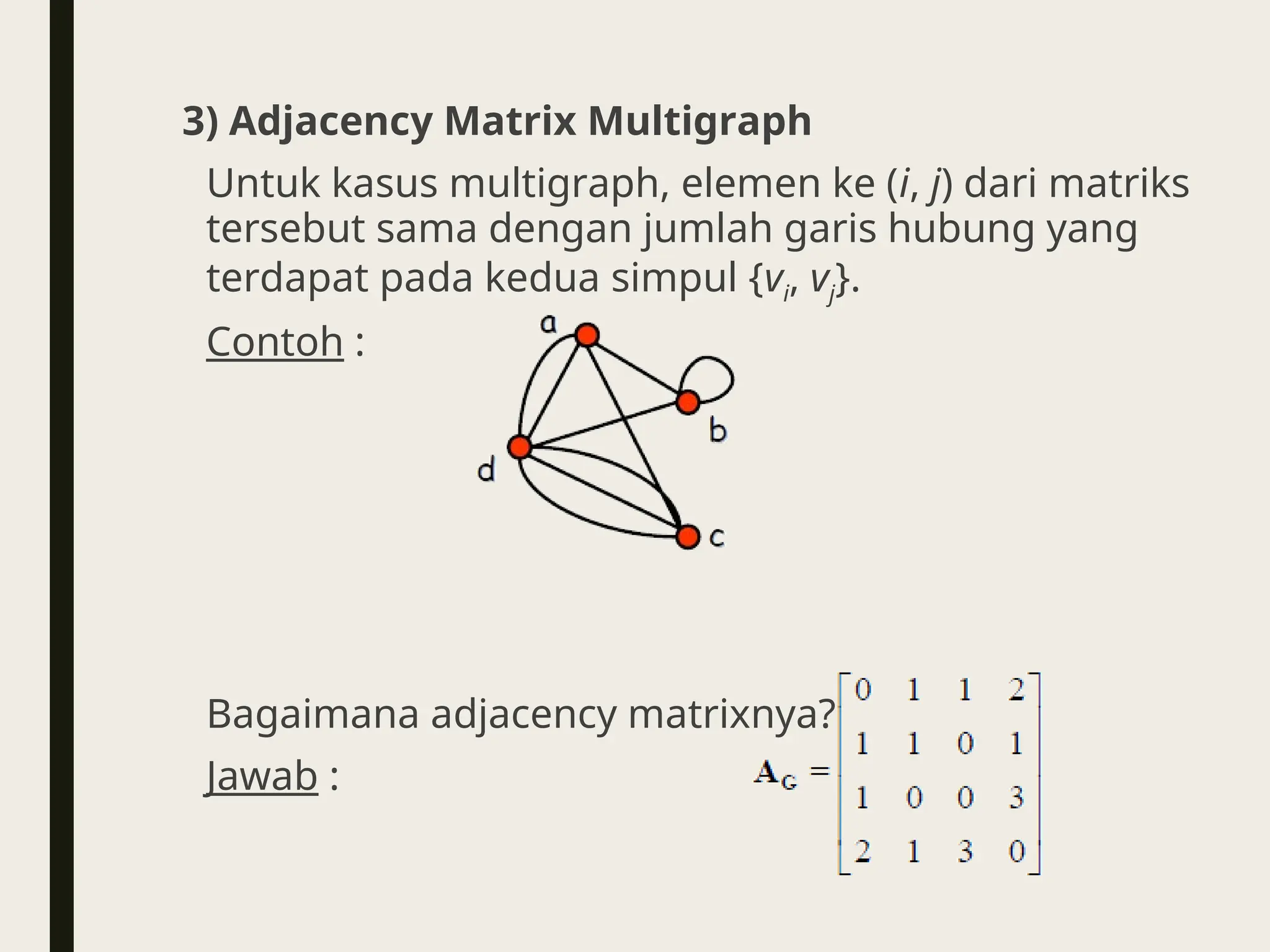
20. 2) Adjacency Matrix
Matriks kedekatan (Adjacency matrix) dari graf G, AG,
yang berkaitan dengan vertex-vertex, adalah sebuah
matriks boolean n×n dengan elemen ke (i, j) berharga 1
jika vi dan vj bertetangga, dan selainnya itu berharga 0.
Dengan kata lain, untuk sebuah matriks kedekatan
AG = [aij], maka berlaku :
Contoh :
Bagaimanakah matrix adjacency yg terbentuk dari
urutan vertex a, b, c, d?

21. 3) Adjacency Matrix Multigraph
Untuk kasus multigraph, elemen ke (i, j) dari matriks
tersebut sama dengan jumlah garis hubung yang
terdapat pada kedua simpul {vi, vj}.
Contoh :
Bagaimana adjacency matrixnya?
Jawab :

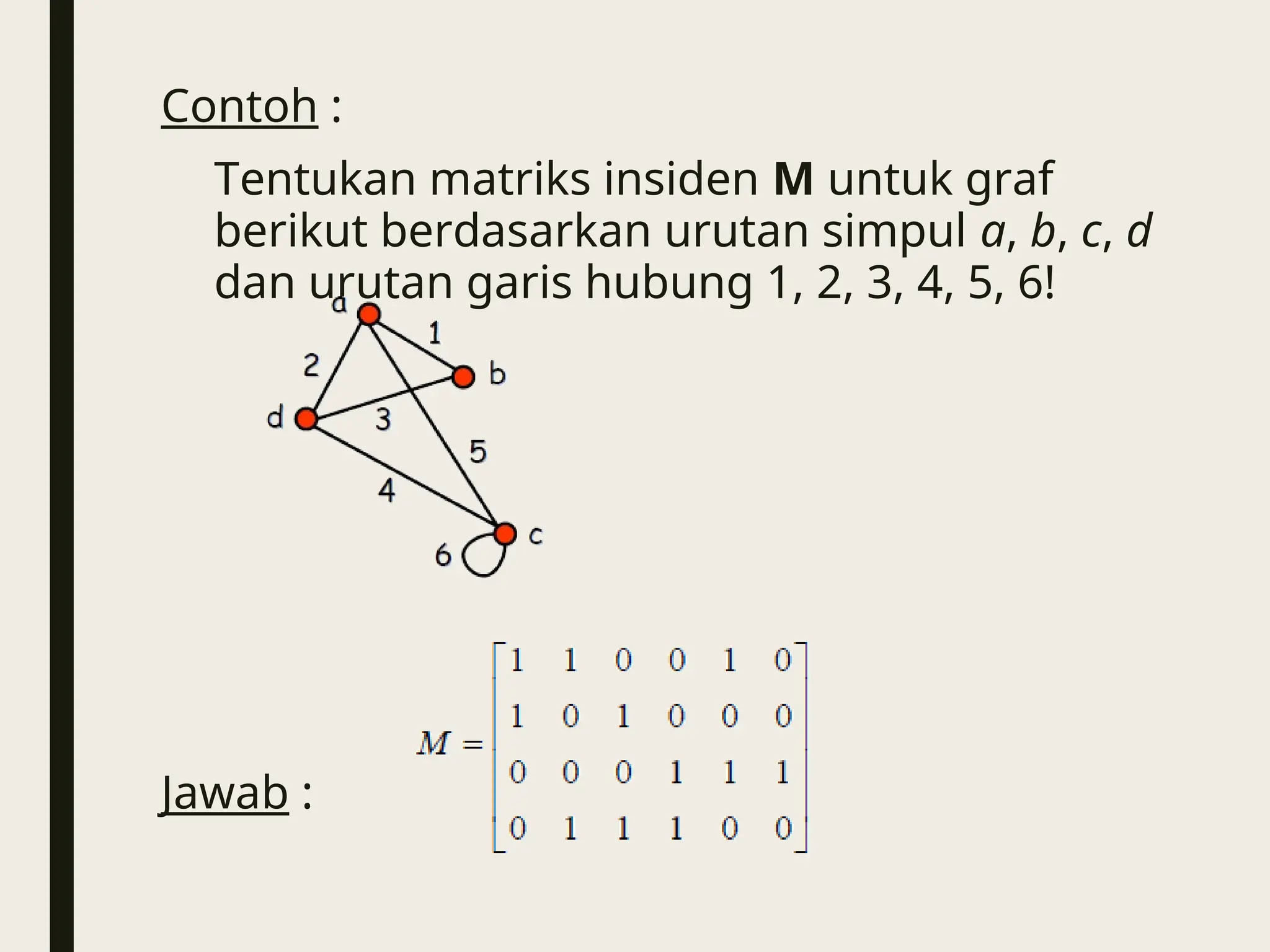
22. 4) Incidence Matrix
Misalkan G = (V, E) sebuah graf tak berarah
dengan |V| = n. Vertex dan edge pada G
disusun dengan urutan seperti v1, v2, …, vn dan
e1, e2, …, em. Matriks insiden (Incidence matrix)
dari G yang berkaitan dengan vertex dan edge
adalah matriks boolean n×m dengan elemen ke
(i, j) =1 jika garis ej terhubung dengan simpul vi,
dan selain itu berharga 0.
Dengan kata lain , untuk sebuah incidence
matrix M = [mij], maka berlaku :

23. Contoh :
Tentukan matriks insiden M untuk graf
berikut berdasarkan urutan simpul a, b, c, d
dan urutan garis hubung 1, 2, 3, 4, 5, 6!
Jawab :

24. Graph Isomorfis
Untuk menentukan dua buah graf tidak
isomorfis atau graf isomorfis, kita dapat memeriksa
invariannya, yaitu sifat yang harus dimiliki oleh dua
buah graf sederhana yang isomorfis. Keduanya
haruslah
- Memiliki jumlah simpul yang sama
- Jumlah garis hubung yang sama
- Derajat dari simpul-simpulnya sama.
Contoh : Apakah graph-graph di bawah ini termasuk
isomorfis?

25. Selesai…