Downloaded 112 times
Uploaded byInsani Mahardhika
Symbolic logic
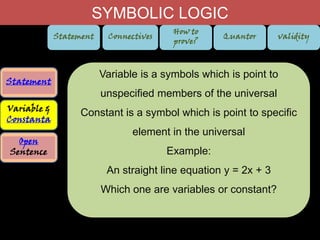
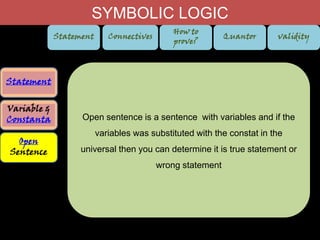
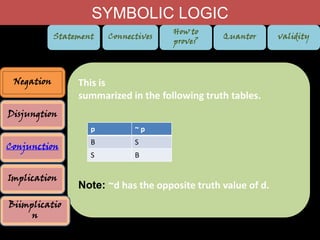
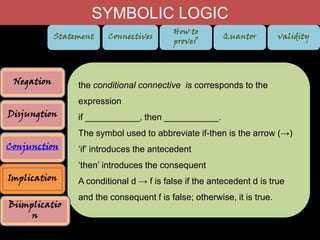
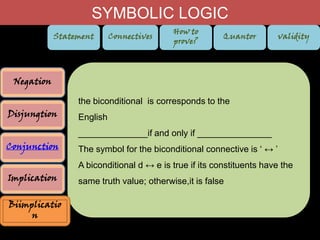
This document discusses the basics of symbolic logic, including: 1. Statements can be true or false, while questions and commands are not statements. Variables refer to unspecified elements while constants refer to specific elements. 2. Connectives like negation, disjunction, conjunction, implication, and biconditional are used to combine statements and change their truth values. 3. Quantifiers like "all" and "some" are used to make statements about variables. Validity refers to whether a conclusion necessarily follows from given premises. Formal systems of logic aim to prove validity through formal rules of inference.
More Related Content
Similar to Symbolic logic
Symbolic logic
- 1.
- 2. SYMBOLIC LOGIC Statement Statement Variable & Constanta Open Sentence Connectives Howto prove? Quantor validity
- 3. SYMBOLIC LOGIC Statement Statement Variable & Constanta Open Sentence Connectives Howto prove? Quantor validity A statement is a declarative sentence, which is to say a sentence that is capable of being true or false. The following are examples of statements. it is raining I am hungry 2+2 = 4 God exists On the other hand the following are examples of sentences that are not statements. are you hungry? shut the door, please #$%@!!! (replace ‘#$%@!!!’ by your favorite expletive)
- 4. SYMBOLIC LOGIC Statement Statement Variable & Constanta Open Sentence Connectives Howto prove? Quantor validity Variable is a symbols which is point to unspecified members of the universal Constant is a symbol which is point to specific element in the universal Example: An straight line equation y = 2x + 3 Which one are variables or constant?
- 5. SYMBOLIC LOGIC Statement Connectives How to prove? Quantor validity Statement Variable& Constanta Open Sentence Open sentence is a sentence with variables and if the variables was substituted with the constat in the universal then you can determine it is true statement or wrong statement
- 6.
- 7. SYMBOLIC LOGIC Statement Negation Disjungtion Connectives How to prove? Quantor validity A(statement) connective is an expression with one or more blanks (places) such that, whenever the blanks are filled by statements the resulting expression is also a statement. Conjunction Simple statement is a a statement that is not constructed out of smaller statements by the application Implication of a statement connective Biimplicatio n constructed from one or more simplestatements by Compound statement is a statement that is the application of a statement connective.
- 8. SYMBOLIC LOGIC Statement Negation Connectives How to prove? Quantor validity Negationof a statement is a new statement which is true if the truth of the first statement is false and Disjungtion conversely. Symbolized by : - or ¬ or ~ Conjunction Means: “ not”, “no”, “it is not true (false) that”, “it cannot Implication Example: Biimplicatio n be that”, it is imposible that”, etc 1. p :This two things are similar 2. ~p: this two things are not simmilar
- 9. SYMBOLIC LOGIC Statement Negation Connectives How to prove? Quantor Thisis summarized in the following truth tables. Disjungtion p Conjunction Implication Biimplicatio n ~p B S S B Note: ~d has the opposite truth value of d. validity
- 10. SYMBOLIC LOGIC Statement Negation Disjungtion Conjunction Implication Biimplicatio n Connectives How to prove? Quantor validity Disjunctionis corresponds roughly to the English ‘or’. The symbol for disjunction is “ ˅ “ (wedge). In English, the word ‘or’ has at least two different meanings, or senses, which are respectively called the exclusive sense and the inclusive sense So there are two types of disjunction: 1. Inclusive Disjunction A disjunction p ˅ q false if both disjuncts are false; is otherwise, it is true 2. Exclusive Disjunction A disjunction p ˅ q false if both disjuncts are the same is truth; otherwise, it is true
- 11. SYMBOLIC LOGIC Statement Connectives How to prove? Quantor validity Negation Conjunctionis corresponds to the English expression Disjungtion „and‟. The symbol for conjunction is “ ˄ “ Conjunction Deffinition: A conjunction p ˄ q is true if both conjuncts are true; Implication Biimplicatio n otherwise, it is false
- 12. SYMBOLIC LOGIC Statement Negation Connectives How to prove? Quantor validity theconditional connective is corresponds to the expression Disjungtion if ___________, then ___________. The symbol used to abbreviate if-then is the arrow (→) Conjunction „if‟ introduces the antecedent „then‟ introduces the consequent Implication Biimplicatio n A conditional d → f is false if the antecedent d is true and the consequent f is false; otherwise, it is true.
- 13. SYMBOLIC LOGIC Statement Connectives How to prove? Quantor validity Negation thebiconditional is corresponds to the Disjungtion English ______________if and only if _______________ Conjunction The symbol for the biconditional connective is „ ↔ ‟ A biconditional d ↔ e is true if its constituents have the Implication Biimplicatio n same truth value; otherwise,it is false
- 14.
- 15.