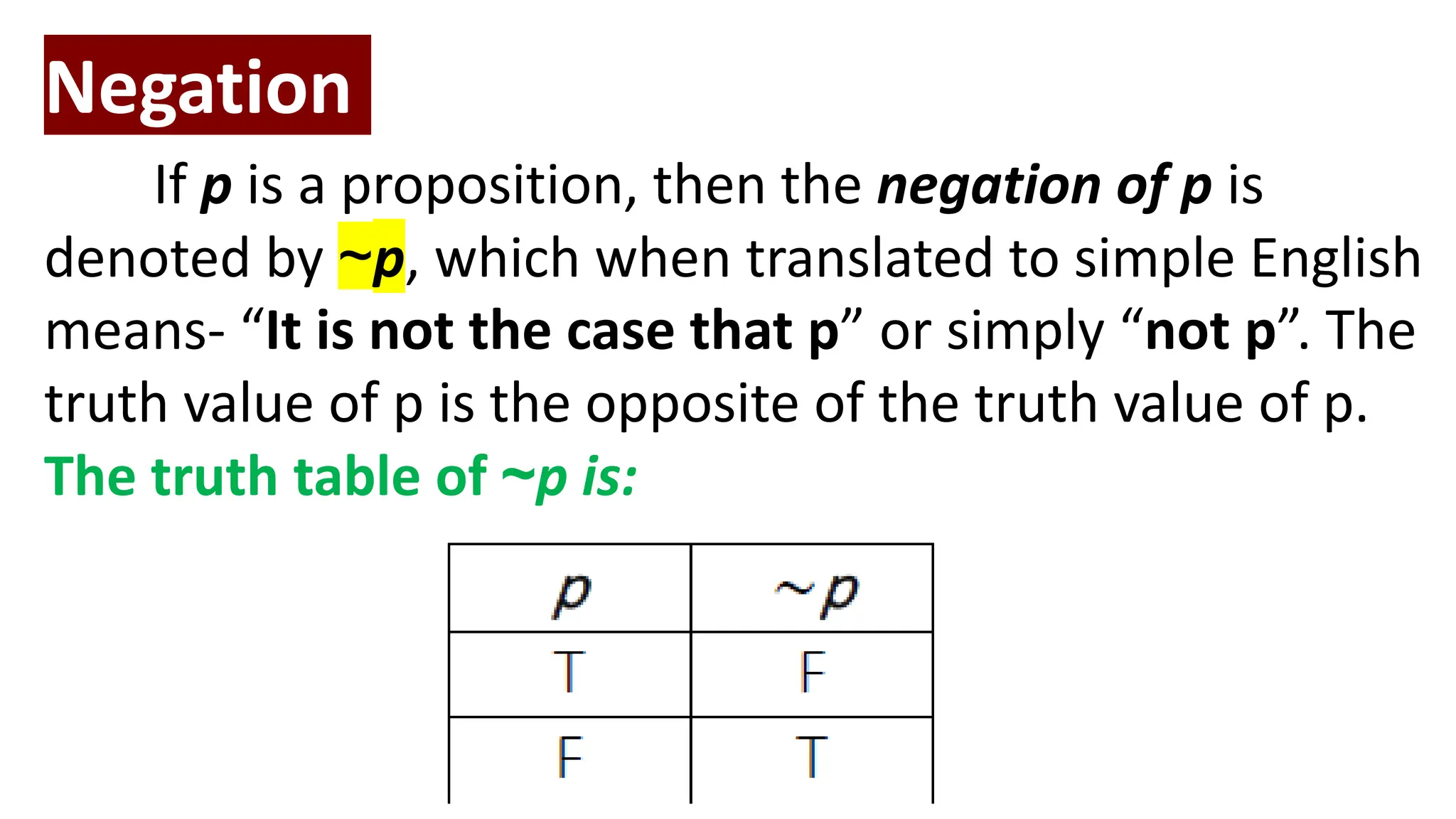
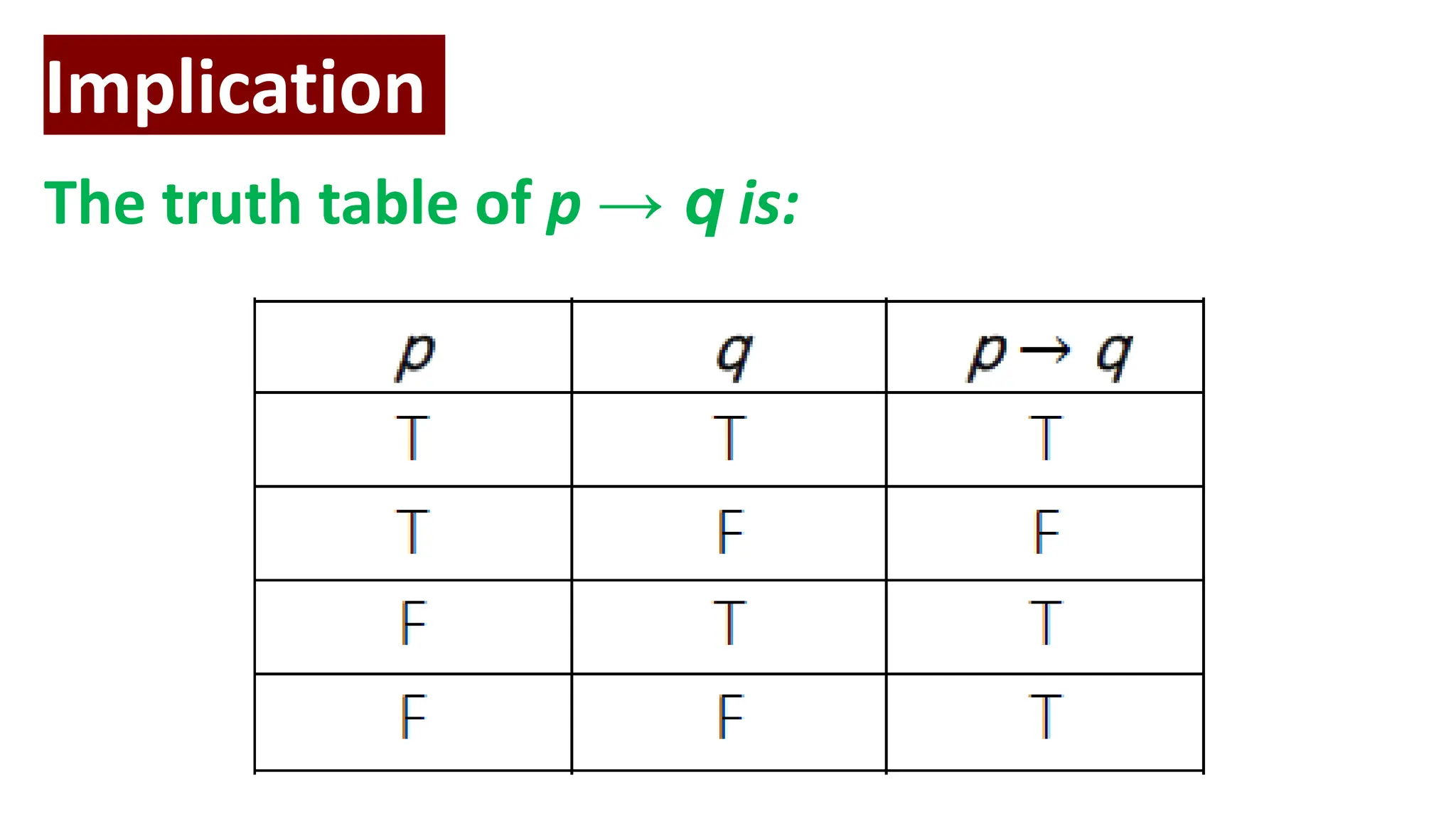
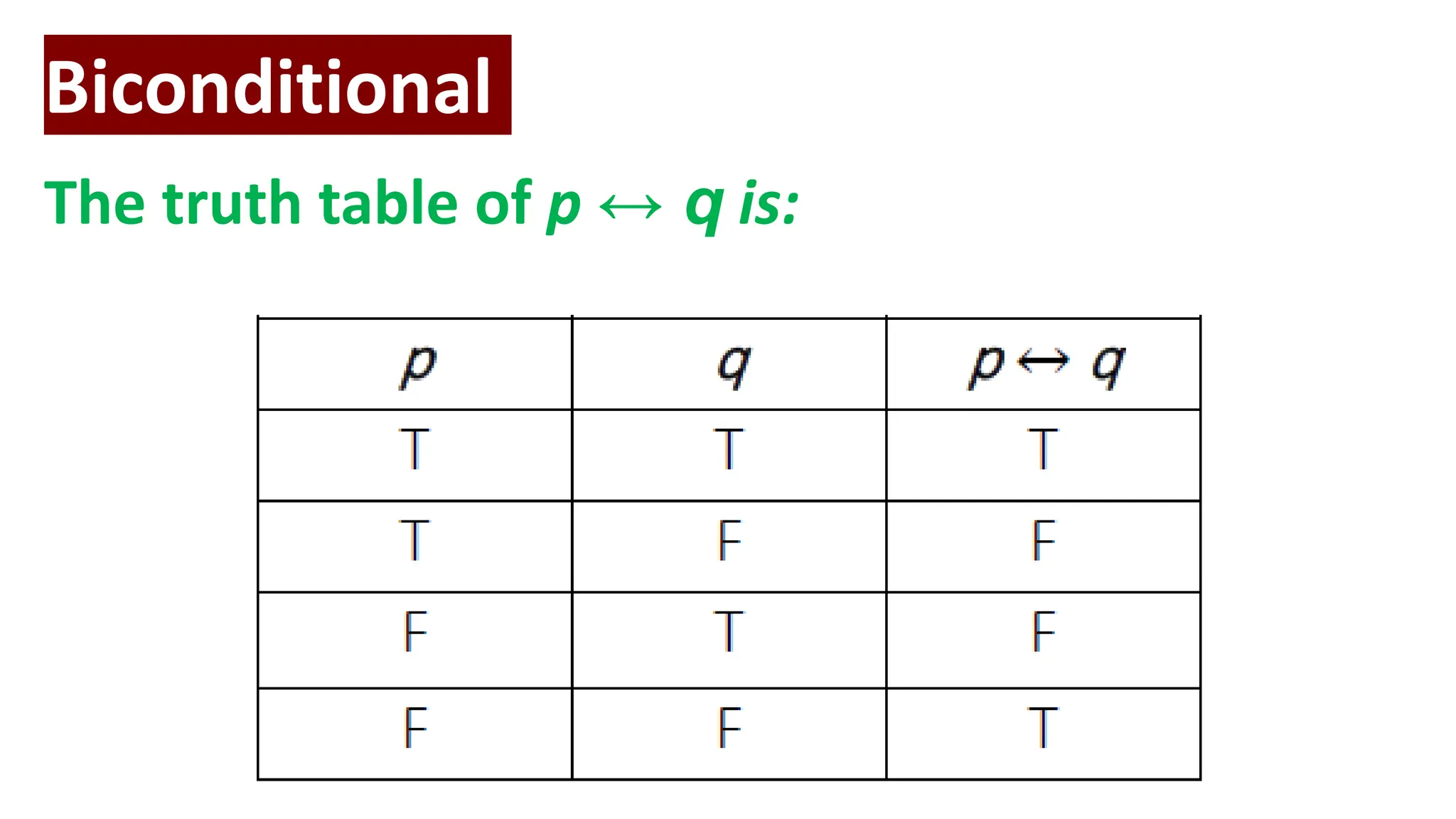
The document discusses logic and propositions. It defines key logic terms like proposition, truth value, statement, simple proposition, compound proposition, connectives, negation, conjunction, disjunction, implication, biconditional, and truth tables. It provides examples and explanations of how to identify, classify, symbolize propositions using logical connectives, and construct truth tables for compound propositions.

1. GENERAL MATHEMATICS
LOGIC

3. Logic
• Crucial for mathematical reasoning
• Logic is a system based on propositions.
Proposition
• A declarative sentence that is either true or
false, but NOT both.
Truth value of a proposition
• is either true (T) or false (F).

4. Identify:
 statement
 proposition and
 truth value

5. “Elephants are bigger than mice.”
Is this a statement?
Is this a proposition?
What is the truth value
of the proposition?
yes
yes
true

6. “520 < 111”
Is this a statement?
Is this a proposition?
What is the truth value
of the proposition?
yes
yes
false

7. “My seatmate will get a perfect score in
the logic exam.”
Is this a statement?
Is this a proposition?
What is the truth value
of the proposition?
yes
yes
It can be either true or false. We
call this propositional function or
open sentence.

8. Simple Propositions
• A proposition that conveys one thought
with no connecting words.

9. Compound Propositions - connectives
• A compound proposition is a proposition
formed from simpler propositions using logical
connectors or some combination of logical
connectors. Some logical connectors involving
propositions p and q maybe expressed as
follows: not p, p and q, p or q, if p then q,
p if and only if q.

10. Examples of Compound Propositions
1. The number 2 is even and the
number 3 is odd.
2. You can have cookies or brownies.
3. If you study hard, then you’ll get
good grades.

12. Truth tables
is a tabular format that
shows the truth or falsity of
a compound statement.

13. Negation
If p is a proposition, then the negation of p is
denoted by ~p, which when translated to simple English
means- “It is not the case that p” or simply “not p”. The
truth value of p is the opposite of the truth value of p.
The truth table of ~p is:

14. Examples of Negation
1. p: Today is Saturday.
~p: Today is not Saturday.
2. p: The coffee is hot.
~p: The coffee is not hot.

15. Conjunction
For any two propositions p and q, their
conjunction is denoted by p ˄ q , which means “p
and q”. We can also use the word but. The
conjunction is true when both p and q are true,
otherwise false.
The truth table of p ˄ q is:

16. Examples of Conjunction
1. p: The book is interesting.
q: I am staying at home.
p ˄ q: The book is interesting, and I am
staying at home.
2. p: 12 is divisible by 3.
q: 3 is a prime number.
p ˄ q: 12 is divisible by 3, and 3 is a prime
number.

17. Disjunction
For any two propositions p and q, their
disjunction is denoted by p ˅ q , which means “p
or q”.
The disjunction is true when either p or q are true,
otherwise false.
The truth table of p ˅ q is:

18. Examples of Disjunction
1. p: I go to the mall.
q: I go to the gym.
p ˅ q: I go to the mall or to the gym.
2. p: I will buy a cellphone.
q: I will eat an ice cream.
p ˅ q: I will buy a cellphone or eat an ice cream.

19. Implication
For any two propositions p and q, the statement “if
p then q” is called an implication and it is denoted by
p→ q.
In the implication p→ q, p is called the hypothesis
or antecedent or premise and q is called the conclusion
or consequence.
The implication p→ q is called a conditional
statement. The implication is false when p is true and q
is false otherwise it is true.

20. The truth table of p → q is:
Implication

21. Examples of Implication
1. p: The book is expensive.
q: The writer is famous.
p → q: If the book is expensive, then the writer is
famous.
2. p: The ice is melting.
q: The temperature is hot.
p ˅ q: If the ice is melting, then the temperature
is hot.

22. Biconditional or Double Implication
For any two propositions p and q, the
statement “p if and only if q” is called
biconditional and it is denoted by p↔ q.
The statement p ↔ q is called a bi-
implication. The implication is true when p
and q have the same truth values, and if
false otherwise.

23. The truth table of p ↔ q is:
Biconditional

24. Examples of Biconditional
1. p: A polygon is a triangle.
q: A polygon has exactly 3 sides.
p ↔ q: A polygon is a triangle if and only if
it has 3 sides.
2. p: I am breathing.
q: I am alive.
p ↔q: I am breathing if and only if I am alive.

25. A. Classify each proposition as simple or
compound. Classify each compound proposition
as a negation, conjunction, disjunction,
conditional, or biconditional.
1.My friend took his master’s degree in Spain.
2. Roses are red, but violets are blue.
3. You are entitled to a 30% discount if you are
a member.

26. A. Classify each proposition as simple or
compound. Classify each compound proposition
as a negation, conjunction, disjunction,
conditional, or biconditional.
4. Roel was on time, but Tom was late.
5. Either he watches a movie or dines with his
friends.
6. If it is an acute angle, then it has less than 90

27. B. Convert each compound proposition into
symbols.
1. He has green thumb and he is a senior
citizen.
2. He does not have green thumb or he is not
a senior citizen.

28. B. Convert each compound proposition into
symbols.
3. It is not the case that he has green thumb
or is a senior citizen.
4. If he has green thumb, then he is not a
senior citizen.

29. E. Let p = Mathematics is difficult, q = PE is
easy, and b = Biology is interesting. Write
each statement in words.

30. Let p = Mathematics is difficult and q = PE is easy.
Write each of the following statements in symbolic
form.
1. If Mathematics is difficult, then PE is easy.
2. It is false that PE is not easy.
3. PE is not easy, and Mathematics is difficult.
4. Mathematics is difficult, or PE is easy.
5. PE is easy if Mathematics is Difficult.

31. Construct a truth table for
a. ~ (p ˄ q)
b. ~ (p ˅ q)
c. ~ (p ˄ ~ q)