Survival analysis

1. Ｒによるデータサイエンス 第１１章 生存分析 @doradora09

2. outline 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

3. outline 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

4. 自己紹介 名前：大城信晃 職業：Ｗｅｂエンジニア（バックエンド） Twitter ： akiaki5516 ( doradora09 ) ＴｏｋｙｏＲでは懇親会の運営 趣味：最近カクテル作り始めました

5. カクテル ソルティドッグ

6. カクテル ソルティドッグ ジョンコリンズ

7. カクテル ソルティドッグ ジョンコリンズ ミュータントタートル

8. 【速報】ＢＡＲドラドラがＯｐｅｎしました！ ３０種類以上のお酒であなたをおもてなし 皆様のご来店お待ちしています！

9. では本題へ

10. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

11. テキスト紹介 毎回恒例のテキスト枠 Ｒによるデータサイエンス http://bit.ly/jgtnBD 第１１章 生存分析 pp183 – 199

12. テキストの無い方は HTML版 Web上で公開されています http://www1.doshisha.ac.jp/~mjin/R/36/36.html

13. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

14. 本スライドの目的 生存分析とは何かわかるようになる 生存分析のグラフが読めるようになる Ｒを使って生存分析のグラフが作成できる ※数式は わからない 時間の都合上省略しているので、気になる方はテキストの方を参考にしてください。

15. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

16. 基本概念 生存時間分析とは 生存時間分析とは、イベントが起きるまでの 時間とイベントの間の関係 に焦点を当てる分析方法 イベント：死亡、故障、解約、倒産、破壊など 分析例 新薬の効果を分析 機械システムや製品の故障 LTV（顧客収益価値）の分析 例：プリペイド携帯電話の顧客がいつ離れるか

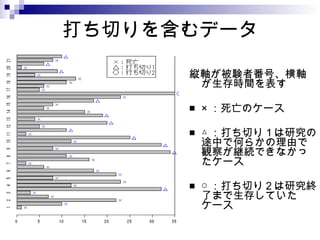
17. 例： 新薬の効果を分析 6-MP という薬を投与した場合とそうでない場合の白血病患者の生存時間のグラフ 縦軸が生存率 横軸が時間 新薬を投与した方が生存確率が高い

18. 例：プリペイド携帯電話の顧客がいつ離れるか プリペイド携帯電話の解約と時間の関係 施策前と施策後の変化を比較する 引用： 顧客収益価値の測定方法 施策後は生存確率が上がった （ = 解約率が減った）

19. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

20. 用語説明 死亡 故障、破壊、倒産、死亡などのイベントの生起のことを 広義の死亡と呼ぶことにする 打ち切り 治療の中止や転院により試験・観察の途中で脱落する場合がある。このような場合を打ち切りが生じたという。 必ずしも最後まで観察データを取れるわけではない (・・あまり縁起のよくない用語が多い)

21. 打ち切りを含むデータ 縦軸が被験者番号、横軸が生存時間を表す × ：死亡のケース △ ：打ち切り１は研究の途中で何らかの理由で観察が継続できなかったケース ○ ：打ち切り２は研究終了まで生存していたケース

22. 生存関数とハザード関数 生存関数Ｓ (t) 累積確率分布関数 F(t) で表すと、イベントがある時点ｔまで生起していない生存関数Ｓ (t) は S(t) = Pr(T > t) = 1 - Pr(t ≦ T) = 1 – F(t) で表される。 ハザード関数 イベントがある時点 t までに生起していないという条件の下で、次の瞬間にイベントが生起する瞬間死亡率 危険度とも呼ばれている。 生存関数とハザード関数は、どちらか片方が分かればもう片方も分かる関係。 ( 数式の詳細は p185 参照 )

23. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

24. 生存時間分析の分類 生存時間に影響を与える時間以外の共変量（複数の要因、説明変数）が パラメータとして作成するモデルに導入されているか否か 生存時間の分布系に特定の確率分布を仮定するか否か によって次の３種類に分類できる

25. 生存時間分析の分類 分布の仮定 共変量の導入 ○ ○ パラメトリック モデル × ○ セミノンパラメトリック モデル × × ノンパラメトリック モデル

26. 補足：パラメトリックとノンパラメトリック パラメトリックな手法 母集団の特性を規定する母数についてある仮説を設けるもので， 平均値の差の検定 （t 検定と略称されることが多い）や 分散分析 （F 検定と略称されることがある）などがこれに該当する。これらの検定手法では，母集団の正規性や 等分散性 が仮定される。 ノンパラメトリックな手法 母集団の分布型（母数）について一切の仮定を設けない。 このため， 分布によらない手法 と呼ばれることもある。 特に， 標本サイズが小さい場合には，それから求められた統計量の分布型は不正確なことが多く，パラメトリックな手法を適用することは不適切になりやすい。 しかし，ノンパラメトリックな手法は常に適用可能である。

27. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

28. ノンパラメトリックモデル 確率分布を仮定せずに生存時間を推定する方法 特徴 共変量を導入しない 分布の仮定をしない 推定法 経験分布による推定法 カプラン - マイヤー推定法が有名 ハザード関数による推定法 ネルソン - アーラン推定量 フレミング - ハリントン推定量

29. Ｒを使って生存解析 生存分析パッケージ survival を利用する データは MASS パッケージの gehan データを用いる 白血病患者に対する薬の効果を調べるために被験者４２名に対して行った臨床試験データ 解析には Surv 関数と survfit 関数を用いる

30. gehanデータの中身 library(survival);library(MASS); data(gehan);dim(gehan); [1] 42 4 gehan[1:6,] pair time cens treat 1 1 1 1 control 2 1 10 1 6-MP 3 2 22 1 control 4 2 7 1 6-MP 5 3 3 1 control 6 3 32 0 6-MP pair : 投薬と比較対象のペア time: 生存時間 cens ：打ち切りか否か (1 が打ち切り ) treat:6-PM( 抑癌薬 ) の投与か否か

31. 解析： Surv, survfit 関数 Surv(time, event) time: 生存時間 event: イベント survfit(formula, data, type=“ “, …) formula : Surv オブジェクト形式の目的変数と説明変数をセットする data : 解析対象のデータ type : 推定方法。デフォルトはカプラン - マイヤー推定法。他にフレミング - ハリントン推定法、 fh2 推定法がある メモ： R からヘルプを出す場合はパッケージ名も指定する ?survival::Surv ?survival::survfit

32. 解析結果 ge.sf <- survfit(Surv(time,cens)~treat, data=gehan); ge.sf; Call: survfit(formula = Surv(time, cens) ~ treat, data =gehan) records n.max n.start events median 0.95LCL 0.95UCL treat=6-MP 21 21 21 9 23 16 NA treat=control 21 21 21 21 8 4 12 records: 対照郡 , n.max: レコード数 n.start: 開始時の数 , median: 中央値 0.95LCL,0.95UCL : 95% 信頼区間の上下限値 6-MP を投与したグループは生存期間の中央値が 23 と大幅に増えている

33. summary(ge.sf) treat=6-MP time n.risk n.event survival std.err lower 95% CI upper 95% CI 6 21 3 0.857 0.0764 0.720 1.000 7 17 1 0.807 0.0869 0.653 0.996 10 15 1 0.753 0.0963 0.586 0.968 13 12 1 0.690 0.1068 0.510 0.935 16 11 1 0.627 0.1141 0.439 0.896 22 7 1 0.538 0.1282 0.337 0.858 23 6 1 0.448 0.1346 0.249 0.807 解析結果詳細 項目左から 生存時間、リスクセット、イベントの数、推定された生存確率、 標準誤差、 95% 信頼区間の上下限値 時間が経つにつれ、推定された生存確率が下がっていく

34. 解析結果をプロット plot(ge.sf) legend(locator(1), c(&quot;6-MP 投与郡 &quot;, &quot; 対照郡 &quot;), lty=c(1,2)); 図からも 6-PM 投与郡のほうが 生存期間が長いことが わかる

35. 投薬郡に対する90%信頼区間 信頼区間に納まっている ge2<-subset(gehan, treat==&quot;6-MP&quot;); ge2.s <- survfit(Surv(time, cens)~treat, conf.int=.9, data=ge2); plot(ge2.s, mark.t=F); legend(locator(1), lty=c(1,2), legend=c(&quot; 生存曲線 &quot;, &quot;90% 信頼区間 &quot;))

36. 信頼区間の推定法 servfit 関数は conf.type パラメータで信頼区間の推定法を変更することができる 種類は以下の通り plain log log-log conf.int パラメータで信頼区間を設定可能 デフォルトは conf.int=.95 (95% の信頼区間 ) コードはテキスト p189 参照

37. 推定法の変更 servfit 関数は conf パラメータで生存期間の推定法を変更することができる 種類は以下の通り デフォルト ( カプラン - マイヤー ) fh ( フレミング - ハリントン ) fh2 コードはテキスト p189 参照

38. 検定： servdiff 関数 ２郡以上の観測値が得られた場合、その優位性の検定が必要する場合がある survdiff (…) 引数 rho=0 でログ･ランク検定 ( デフォルト ) 引数 rho=1 でゲーハン - ウィルコソン検定

39. 検定： servdiff 関数 実行結果 survdiff(Surv(time)~treat, data=gehan) Call: survdiff(formula = Surv(time) ~ treat, data = gehan) N Observed Expected (O-E)^2/E (O-E)^2/V treat=6-MP 21 21 29.2 2.31 8.97 treat=control 21 21 12.8 5.27 8.97 Chisq= 9 on 1 degrees of freedom, p= 0.00275 ログ･ランク検定の p 値は約 0.003 なので、有意水準 5% とすると 両群の生存曲線には優位な差が認められる。

40. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

41. セミノンパラメトリックモデル 分布の仮定 共変量の導入 ○ ○ パラメトリック モデル × ○ セミノンパラメトリック モデル × × ノンパラメトリック モデル

42. セミノンパラメトリックモデル 特徴 共変量を導入する 分布の仮定をしない イベントに影響を及ぼす複数の因子（共変量）の影響を解析することを前提としたノンパラメトリックモデルのこと 共変量としては、年齢や血圧のような連続変数、性別や結婚の有無のようなカテゴリカル変数、これらの交差項などを含む変数ベクトル モデル コックス比例ハザードモデル が良く用いられる ( 数式はテキスト p191)

43. コックス比例ハザードモデル パラメータの推定 直接法 ブレスロー (Breslow) の近似法 エフロン (Efron) の近似法 イベントの数が増えると近似法のほうが計算が簡単であるが、同時に起こるイベントの数が多くなった場合妥当性を失うといわれている Survival パッケージには関数 coxph がある

44. 推定： Coxph 関数 coxph(formula, data, method, … ) formula: 共変量など data: データ method : 以下の３種類。デフォルトは’ efron’ efron breslow exact

45. データ：kidney ポータブル透析装置の使用と腎臓患者の生存時間に関して、38ペア(使用と不使用）に対する実験データ parent: ID time: 時間 status:打ち切りは0, その他は1 age: 年齢 sex: 男性 =1, 女性 =2 disease: 病気の種類 (GN, AN, PKD, Other) frail: オリジナル論文からのフレイルティの推定値

46. 解析例：コックスハザードモデル 性別 (sex) と病気の種類 (disease) を説明変数とした解析例 data(kidney) kidney.cox<- coxph( Surv(time, status)~sex+disease, data=kidney) summary(kidney.cox); Call: coxph(formula = Surv(time, status) ~ sex + disease, data = kidney) n= 76 coef exp(coef) se(coef) z Pr(>|z|) sex -1.4774 0.2282 0.3569 -4.140 3.48e-05 *** diseaseGN 0.1392 1.1494 0.3635 0.383 0.7017 diseaseAN 0.4132 1.5116 0.3360 1.230 0.2188 diseasePKD -1.3671 0.2549 0.5889 -2.321 0.0203 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

47. 解析例：コックスハザードモデル ３種類の検定統計量を返す 尤度比の検定、ワルド検定、スコア検定 exp(coef) exp(-coef) lower .95 upper .95 sex 0.2282 4.3815 0.11339 0.4594 diseaseGN 1.1494 0.8700 0.56368 2.3437 diseaseAN 1.5116 0.6616 0.78245 2.9202 diseasePKD 0.2549 3.9238 0.08035 0.8084 Rsquare= 0.206 (max possible= 0.993 ) Likelihood ratio test= 17.56 on 4 df, p=0.001501 Wald test = 19.77 on 4 df, p=0.0005533 Score (logrank) test = 19.97 on 4 df, p=0.0005069

48. 生存時間の推定： survfit 構築したモデルによる生存時間の当てはめは、関数 survfit を用いると便利 kidney.fit<-survfit(kidney.cox); summary(kidney.fit); Call: survfit(formula = kidney.cox) time n.risk n.event survival std.err lower 95% CI upper 95% CI 2 76 1 0.99018 0.00985 0.971059 1.000 7 71 2 0.96856 0.01831 0.933335 1.000 ・・・ 536 2 1 0.01224 0.01383 0.001336 0.112 562 1 1 0.00318 0.00613 0.000073 0.139

49. プロット plot(kidney.fit); survfit で推定された生存曲線および信頼区間 信頼区間内に納まっている

50. 残差分析 打ち切りデータがあるため、残差分析が少々複雑になる 提案されている残差 ( カッコ内は指定パラメータ ) マルチンゲール残差 ( デフォルト ) 良く使われている シェーンフィールド残差 (type=“schoen-feld”) スコア残差 (type=“score”) デヴィアンス残差 (type=“deviance”) 関数 coxph のモデルの残差は residuals.coxph( 略して residuals) 関数で呼び出す パラメータ type を変えることで残差の種類を切り替えられる

51. マルチンゲール残差プロット scatter.smooth( residuals(kidney.cox )); abline(h=0,lty=3,col=2); １が上限で下限値は無し 明らかに変化パターンがなければＯＫ これを標準化したのが次のデヴィアンス残差

52. デヴィアンス残差プロット scatter.smooth(residuals(kidney.cox, type=&quot;deviance&quot; )); abline(h=0,lty=3,col=2); 標準化されている

53. ハザードの比例性の分析 コックス比例ハザードモデルは、ハザード比が時間によらず一定であることを前提としているため、その仮定を吟味する必要がある。 関数 cox.zph を用いる デフォルトは Kaplan-Meier 推定量

54. 比例性の分析： cox.zph kidney.zph<- cox.zph(kidney.cox); kidney.zph rho chisq p sex 0.18839 2.60676 0.106 diseaseGN -0.01392 0.01123 0.916 diseaseAN 0.06162 0.20036 0.654 diseasePKD 0.00701 0.00438 0.947 GLOBAL NA 4.20781 0.379

55. 比例性の診断プロット スプライン平滑化曲線に、時間に伴う明らかな変化パターンが無ければ比例ハザードの仮定には問題がないといわれている。 op<- par(mfrow=c(2,2), mar=c(4.5,4,1,1)); plot(kidney.zph,df=2); par(op);

56. 交互作用と変数の選択 コックス比例ハザードモデルの場合でも、説明変数の交互作用を取りれたも出るの構築ｶﾞ可能。 詳細はテキスト参照。

57. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

58. パラメトリックモデル 分布の仮定 共変量の導入 ○ ○ パラメトリック モデル × ○ セミノンパラメトリック モデル × × ノンパラメトリック モデル

59. パラメトリックモデル 特徴 共変量を導入する 分布の仮定をする コックス比例ハザードモデルに比べると計算速度が速い ただし、制約のため応用範囲が限定される 生存時間が確率分布に従うという仮定の下で構築したモデル survreg(formula=formula(data), dist=“weibull”, …) 分布 指数分布 (dist=exponential) ワイブル (dist= デフォルト ) 対数正規 (dist=log-normal) ロジスティック (dist=logistic) 対数ロジスティック (dist=log-logistic) ( 数式はテキスト p198 参照 )

60. 解析： survreg 関数 survreg(Surv(time, status)~ sex+disease, kidney, dist=&quot;lognormal&quot;); Call: survreg(formula = Surv(time, status) ~ sex + disease, data = kidney, dist = &quot;lognormal&quot;) Coefficients: (Intercept) sex diseaseGN diseaseAN diseasePKD 1.7923643 1.5062960 -0.3334601 -0.5321264 0.6810495 Scale= 1.129394 Loglik(model)= -329.1 Loglik(intercept only)= -340 Chisq= 21.8 on 4 degrees of freedom, p= 0.00022 n= 76

61. 自己紹介 テキスト紹介 本スライドの目的 基本概念 用語説明 生存時間分析の分類 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル まとめ

62. まとめ 生存分析はイベントが起きるまでの時間を分析する手法 打ち切りが発生する 大きく３種類のモデルがある。 ノンパラメトリックモデル セミノンパラメトリックモデル パラメトリックモデル Ｒではそれぞれに対応した関数とデータが用意されている

63. ご清聴ありがとうございました。