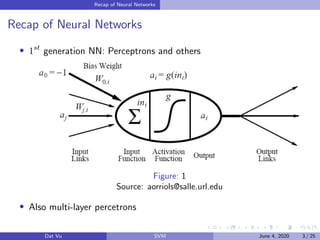
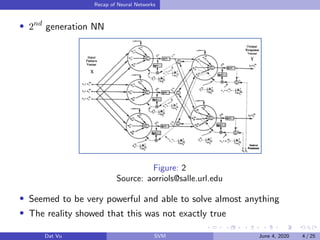
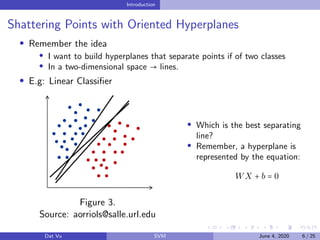
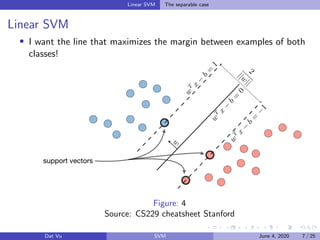
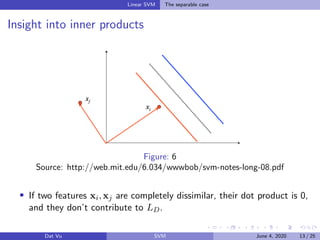
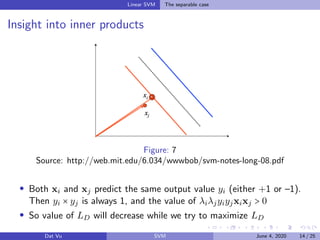
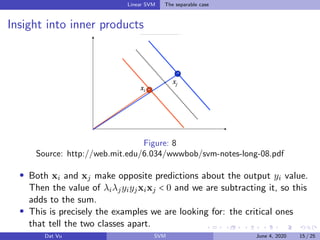
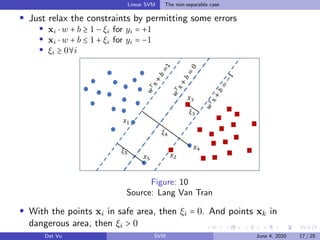
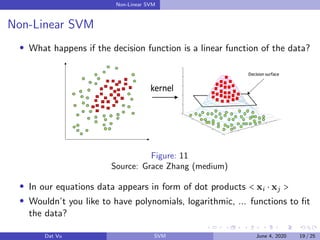
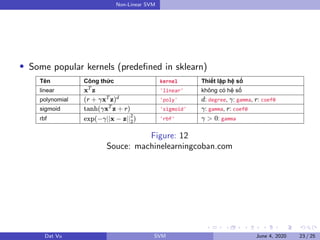
This document summarizes a presentation on support vector machines (SVMs). It begins with a recap of neural networks and then provides an introduction to SVMs, explaining how they use hyperplanes to separate data points of different classes. It covers linear SVMs for both separable and non-separable data, explaining how support vectors and slack variables handle non-separable cases. It concludes by discussing how kernels allow SVMs to find non-linear decision boundaries by projecting data into higher-dimensional spaces.

1. Artificial Intelligence Club
Support Vector Machines
June 4, 2020
Dat Vu SVM June 4, 2020 1 / 25

2. Today’s agenda:
1 Recap of Neural Networks
2 Introduction
3 Linear SVM
The separable case
The non-separable case
4 Non-Linear SVM
Dat Vu SVM June 4, 2020 2 / 25

3. Recap of Neural Networks
Recap of Neural Networks
1st
generation NN: Perceptrons and others
Figure: 1
Source: aorriols@salle.url.edu
Also multi-layer percetrons
Dat Vu SVM June 4, 2020 3 / 25

4. Recap of Neural Networks
2nd
generation NN
Figure: 2
Source: aorriols@salle.url.edu
Seemed to be very powerful and able to solve almost anything
The reality showed that this was not exactly true
Dat Vu SVM June 4, 2020 4 / 25

5. Introduction
Introduction
SVM (Vapnik, 1995)
Clever type of perception
Instead of hand-coding the layer of non-adaptive features, each training
example is used to create a new feature using a fixed recipe
A clever optimization technique is used to select the best subset of
features
Many NNs researchers switched to SVM in the 1990s because they
work better
Here, we’ll take a slow path into SVM concepts
Dat Vu SVM June 4, 2020 5 / 25

6. Introduction
Shattering Points with Oriented Hyperplanes
Remember the idea
I want to build hyperplanes that separate points if of two classes
In a two-dimensional space → lines.
E.g: Linear Classifier
Figure 3.
Source: aorriols@salle.url.edu
Which is the best separating
line?
Remember, a hyperplane is
represented by the equation:
WX + b = 0
Dat Vu SVM June 4, 2020 6 / 25

7. Linear SVM The separable case
Linear SVM
I want the line that maximizes the margin between examples of both
classes!
Figure: 4
Source: CS229 cheatsheet Stanford
Dat Vu SVM June 4, 2020 7 / 25

8. Linear SVM The separable case
Linear SVM
In more detail
Let’s assume two classes
yi = {−1,1}
Each example described by a set of features x (x is a vector; for clarity,
we will mark vectors in bold in the remainder of the slides)
The problem can be formulated as follows
All training must satisfy (in the separable case)
xi ⋅ w + b ≥ +1,∀yi = +1
xi ⋅ w + b ≤ −1,∀yi = −1
This can be combined
yi(xi ⋅ w + b) ≥ 1,∀i
Dat Vu SVM June 4, 2020 8 / 25

9. Linear SVM The separable case
Support Vectors
What are the support vectors?
Let’s find the points that lay on the hyper plane H1: xi ⋅ w + b = 1
Their perpendicular distance to the origin is:
1 − b
w
Let’s find the points that lay on the hyper plane H2: xi ⋅ w + b = −1
Their perpendicular distance to the origin is:
− 1 − b
w
Figure 5.
Source: aorriols@salle.url.edu
The margin is:
2
w
Dat Vu SVM June 4, 2020 9 / 25

10. Linear SVM The separable case
Therefore, the problem is
Find the hyperplane that minimizes w 2
Subject to yi(xi ⋅ w + b) − 1 ≥ 0∀i
But let us change to the Lagrange formulation because
The constraints will be placed on the Lagrange multipliers themselves
(easier to handle)
Training data will appear only in form of dot products between vectors
Dat Vu SVM June 4, 2020 10 / 25

11. Linear SVM The separable case
The Lagrangian formulation comes to be
Lp =
1
2
w 2
−
l
∑
i=1
λiyi(xi ⋅ w + b) +
l
∑
i=1
λi
Where λi are the Lagrange multipliers, l is the # of training points
Subject to ∀i,λi ≥ 0
So we need to
Minimize Lp w.r.t w,b
Simultaneously require that the derivatives of Lp w.r.t to λ vanish
All subject to the constraints λi ≥ 0
Dat Vu SVM June 4, 2020 11 / 25

12. Linear SVM The separable case
Dual Problem
Transformation to the dual problem
Kuhn-Tucker theorem: The solution we find here will be the same as
the solution to the original problem
This a convex problem
We can equivalently solve the dual problem
That is, maximize LD
LD = ∑
i
λi −
1
2
∑
i,j
λiλjyiyj < xi ⋅ xj >
W.r.t λi
Subject to constrains ∑
i
λiyi = 0
And with λi ≥ 0
Why we want to transform to the dual problem?
Dat Vu SVM June 4, 2020 12 / 25

13. Linear SVM The separable case
Insight into inner products
Figure: 6
Source: http://web.mit.edu/6.034/wwwbob/svm-notes-long-08.pdf
If two features xi,xj are completely dissimilar, their dot product is 0,
and they don’t contribute to LD.
Dat Vu SVM June 4, 2020 13 / 25

14. Linear SVM The separable case
Insight into inner products
Figure: 7
Source: http://web.mit.edu/6.034/wwwbob/svm-notes-long-08.pdf
Both xi and xj predict the same output value yi (either +1 or –1).
Then yi × yj is always 1, and the value of λiλjyiyjxixj > 0
So value of LD will decrease while we try to maximize LD
Dat Vu SVM June 4, 2020 14 / 25

15. Linear SVM The separable case
Insight into inner products
Figure: 8
Source: http://web.mit.edu/6.034/wwwbob/svm-notes-long-08.pdf
Both xi and xj make opposite predictions about the output yi value.
Then the value of λiλjyiyjxixj < 0 and we are subtracting it, so this
adds to the sum.
This is precisely the examples we are looking for: the critical ones
that tell the two classes apart.
Dat Vu SVM June 4, 2020 15 / 25

16. Linear SVM The non-separable case
What if I can not separate the two classes
Figure: 9
Source: aorriols@salle.url.edu
We will not be able to solve the Lagrangian formulation proposed
Any idea?
Dat Vu SVM June 4, 2020 16 / 25

17. Linear SVM The non-separable case
Just relax the constraints by permitting some errors
xi ⋅ w + b ≥ 1 − ξi for yi = +1
xi ⋅ w + b ≤ 1 + ξi for yi = −1
ξi ≥ 0∀i
Figure: 10
Source: Lang Van Tran
With the points xi in safe area, then ξi = 0. And points xk in
dangerous area, then ξi > 0
Dat Vu SVM June 4, 2020 17 / 25

18. Linear SVM The non-separable case
That means that the Lagrangian is rewritten
We change the objective function to be minimized to
1
2
w 2
+ C(
l
∑
i
ξi)
Therefore, we are maximizing the margin and minimizing the error
C is a constant tot be chosen by the user
The dual problem becomes
LD = ∑
i
λi −
1
2
∑
i,j
λiλjyiyj < xi ⋅ xj >
Subject to 0 < λi < C and ∑
i
λiyi = 0
Dat Vu SVM June 4, 2020 18 / 25

19. Non-Linear SVM
Non-Linear SVM
What happens if the decision function is a linear function of the data?
Figure: 11
Source: Grace Zhang (medium)
In our equations data appears in form of dot products < xi ⋅ xj >
Wouldn’t you like to have polynomials, logarithmic, ... functions to fit
the data?
Dat Vu SVM June 4, 2020 19 / 25

20. Non-Linear SVM
Kernel SVM
So far, both hard-margin and soft-margin SVM are linear classifiers.
How do we come up with non-linear classifier?
Idea:
1 Project data onto a space of higher (or even infinite) dimensions
2 Separate new data with a linear classifier (like hard- or softmargin
SVMs)
3 Project the separating hyperplane back to the original space
A beautiful illustration of this idea is Here
Dat Vu SVM June 4, 2020 20 / 25

21. Non-Linear SVM
Kernel function
To project to higher dimension, we need a feature mapping:
φ Rn
→ RN
,N ≫ n
Example: From 3 dimensions to 9-dimensional space
φ
⎡
⎢
⎢
⎢
⎢
⎢
⎣
x1
x2
x3
⎤
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
x1 x1
x1 x2
x1 x3
x2 x1
x2 x2
x2 x3
x3 x1
x3 x2
x3 x3
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Dat Vu SVM June 4, 2020 21 / 25

22. Non-Linear SVM
Kernel Trick
So, the function we end up optimizing is
LD = ∑
i
λi −
1
2
∑
i,j
λiλjyiyjK < xi ⋅ xj >
We define a kernel function
K(xi,xj) = Φ(xi) ⋅ Φ(xj)
An example: K(xi,xj) = e
− xi−xj
2
2σ2
All we have talked about still holds when using the kernel function
Dat Vu SVM June 4, 2020 22 / 25

23. Non-Linear SVM
Some popular kernels (predefined in sklearn)
Figure: 12
Souce: machinelearningcoban.com
Dat Vu SVM June 4, 2020 23 / 25

24. Non-Linear SVM
References
1 Albert Orriols aorriols@salle.url.edu.
2 An Idiot’s guide to Support vector machines (SVMs).
3 Support Vector Machines CS229
4 VEF Academy
5 Machinelearningcoban.com
Dat Vu SVM June 4, 2020 24 / 25