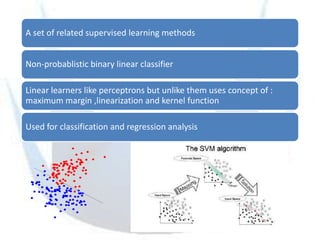
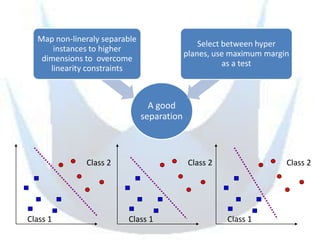
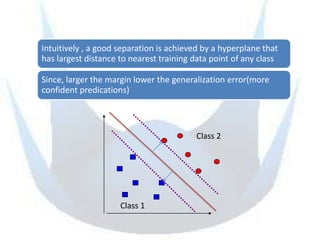
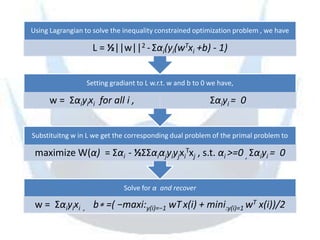
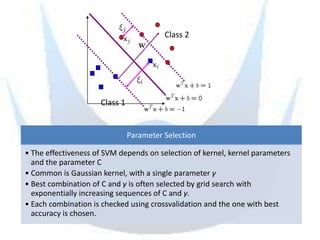
SVM is a supervised learning method that finds a hyperplane with maximum margin to separate classes. It uses kernels to map data to higher dimensions to allow for nonlinear separation. The objective is to minimize training error and model complexity by maximizing the margin between classes. SVMs solve a convex optimization problem that finds support vectors and determines the separating hyperplane using kernels, slack variables, and a cost parameter C to balance margin and errors. Parameter selection, like the kernel and its parameters, affects performance and is typically done through grid search and cross-validation.

1. Submitted by:
Garisha Chowdhary ,
MCSE 1st year,
Jadavpur University

2. A set of related supervised learning methods
Non-probablistic binary linear classifier
Linear learners like perceptrons but unlike them uses concept of :
maximum margin ,linearization and kernel function
Used for classification and regression analysis

3. Map non-lineraly separable
Select between hyper
instances to higher
planes, use maximum margin
dimensions to overcome
as a test
linearity constraints
A good
separation
Class 2 Class 2 Class 2
Class 1 Class 1 Class 1

4. Intuitively , a good separation is achieved by a hyperplane that
has largest distance to nearest training data point of any class
Since, larger the margin lower the generalization error(more
confident predications)
Class 2
Class 1

5. • {(x1,y1), (x2,y2), … , (xn,yn)
Given N samples • Where y = +1/ -1 are labels of data, x belongs to Rn
Find a hyperplane • wTxi+ b > 0 : for all i such that y=+1
wTx + b =0 • wTxi+ b < 0 : for all i such that y=-1
Functional Margin
• With respect to the training example, defined by
ˆγ(i)=y(i)(wT x(i) + b).
• Want functional margin to be large i.e. y(i)(wT x(i) + b) >> 0
• May rescale w and b, without altering the decision function
but multiplying functional margin by the scale factor
• Allows us to impose a normalization condition ||w|| = 1 and
consider the functional margin of (w/||w||,b/||w||)
• w.r.t. training set defined by ˆγ = min ˆγ(i) for all i

6. Geometric margin
• Defined by γ(i)=y(i)((w/||w||)Tx(i)+b/||w||).
• If ||w|| = 1, functional margin = geometric margin
• Invariant to scaling of parameters w and b. w may be scaled such
that ||w|| = 1
• Also, γ = min γ(i) for all i
Now, Objective is to
Maximize γ w.r.t. γ,w,b s.t. Maximize ˆγ/||w|| w.r.t. ˆγ,w,b s.t.
• y(i)(wTx(i) +b) >= γ for all i • y(i)(wTx(i) +b) >= ˆγ for all i
• ||w|| = 1
• Intrducing the scaling constraint that the functional margin be 1, the objective
function may further be simplified as to maximize 1/||w|| , or
Minimize (1/2)(||w||2) s.t.
• y(i)(wTx(i) +b) >= 1

7. Using Lagrangian to solve the inequality constrained optimization problem , we have
L = ½||w||2 - Σαi(yi(wTxi +b) - 1)
Setting gradiant to L w.r.t. w and b to 0 we have,
w = Σαiyixi for all i , Σαiyi = 0
Substituitng w in L we get the corresponding dual problem of the primal problem to
maximize W(α) = Σαi - ½ΣΣαiαjyiyjxiTxj , s.t. αi >=0 , Σαiyi = 0
Solve for α and recover
w = Σαiyixi , b∗ =( −maxi:y(i)=−1 wT x(i) + mini:y(i)=1 wT x(i))/2

8. For conversion of primal problem to dual problem the
following Karish-Kuhn-Tucker conditions must be satisfied
• (∂/∂wi)L(w, α) = 0, i = 1, . . . , n
• αi gi(w,b) = 0, i = 1, . . . , k
• gi(w,b) <= 0, i = 1, . . . , k
• αi >= 0
From the KKT complementary condition(2nd)
• αi > 0 => gi(w,b) = 0 (active constraint) => x(i),y(i) has functional margin 1
(support vectors)
• gi(w,b) < 0 => αi = 0 (inactive constraint, non-support vectors)
Support vectors
Class 2
Class 1

9. In case of non-linearly separable data , mapping data to high
dimensional feature space via non linear mapping function, φ increases
the likelihood that data is linearly separable
Use of kernel function, to simplify computations over high dimensional
mapped data, that corresponds to dot product of some non-linear
mapping of data
Having found αi , calculate a quantity that depends only on the inner
product between x (test point) and support vectors
Kernel function is the measure of similarity between the 2 vectors
A kernel function is valid if it satisfies the Mercer Theorem which states
that the corresponding kernel matrix must be symmetric positive semi-
definite (zTKz >= 0 )

10. Polynomial kernel with degree d
• K(x,y) = (xy + 1 )^d
Radial basis function kernel with width
• K(x,y) = exp(-||x-y||2/(2
• Feature space is infinite dimensional
Sigmoid with parameter and
• K(x,y) = tanh( xTy+
• It does not satisfy the Mercer condition on all and

11. High dimensionality doesn’t guarantee linear separation; hypeplane might be
susceptible to outliers
Relax the constraint introducing ‘slack variables’, ξi, that allow violations of
constraint by a small quantity
Penalize the objective function for violation
Parameter C will control the trade off between penalty and margin.
So the objective now becomes, to minw,b,γ (1/2)||w||2 + C Σξi s.t.
y(i)(wTx(i)+b)>= 1 – ξi, ξi >=0
Tries to ensure that most examples have functional margin atleast 1
Formind the corresponding Lagrangian , the dual problem now is to:
maxαΣαi - ½ΣΣαiαjyiyjxiTxj , s.t. 0<=αi <= C , Σαiyi = 0 .

12. Class 2
Class 1
Parameter Selection
• The effectiveness of SVM depends on selection of kernel, kernel parameters
and the parameter C
• Common is Gaussian kernel, with a single parameter γ
• Best combination of C and γ is often selected by grid search with
exponentially increasing sequences of C and γ.
• Each combination is checked using crossvalidation and the one with best
accuracy is chosen.

13. Drawbacks
• Cannot be directly applied to
multiclass problems, but need use
of algorithms that convert
multiclass problem to multiple
binary class problems
• Uncalibrated class membership
probabilities