Solution homework2
•
1 like•192 views
The document provides solutions to three problems involving finite element analysis. Problem 1 shows the derivation of the weak form of a partial differential equation. Problem 2 sets up finite element models for a bar with two elements, assembles the stiffness matrix and load vector, and solves for displacements and stresses. Problem 3 models a problem with two linear elements, derives the finite element equations, and solves for displacements and stresses, then compares to an exact solution and a single quadratic element solution.
![1
ES 128: Homework 2
Solutions
Problem 1
Show that the weak form of
02)( =+ x
dx
du
AE
dx
d
on 31 << x ,
1.0)1(
1
=
=
=xdx
du
Eσ ,
001.0)3( =u
is given by
∫∫ +−= =
3
1
1
3
1
2)(1.0 xwdxwAdx
dx
du
AE
dx
dw
x w∀ with 0)3( =w .
Solution
We multiply the governing equation and the natural boundary condition over the
domain [1, 3] by an arbitrary weight function:
02
3
1
=
+
∫ dxx
dx
du
AE
dx
d
w )(xw∀ , (1.1)
01.0
1
=
−
=x
dx
du
EwA )1(w∀ . (1.2)
We integrate (1.1) by parts as
dx
dx
du
AE
dx
dw
dx
du
wAEdx
dx
du
AE
dx
d
w
x
x
∫∫
−
=
=
=
3
1
3
1
3
1
. (1.3)
Substituting (1.3) into (1.1) gives
02
13
3
1
3
1
=
−
++
−
==
∫∫
xx
dx
du
wAE
dx
du
wAEwxdxdx
dx
du
AE
dx
dw
)(xw∀ . (1.4)
With 0)3( =w and 1.0)1( =σ , we obtain
( ) 1
3
1
3
1
1.02 =
−=
∫∫ x
wAwxdxdx
dx
du
AE
dx
dw
)(xw∀ with 0)3( =w . (1.5)](https://image.slidesharecdn.com/solutionhomework2-191026054137/85/Solution-homework2-1-320.jpg)
![2
El (1)
El (2)
1
2
3
Figure 1a
x
Problem 2
Consider the (steel) bar in Figure 1. The bar has
a uniform thickness t=1cm, Young’s modulus
E=200 9
10× Pa, and weight density
ρ =7 3
10× 3
/mkg . In addition to its self-weight,
the bar is subjected to a point load P=100N at
its midpoint.
(a) Model the bar with two finite elements.
(b) Write down expressions for the element
stiffness matrices and element body force
vectors.
(c) Assemble the structural stiffness matrix
K and global load vector F .
(d) Solve for the global displacement vector
d.
(e) Evaluate the stresses in each element.
(f) Determine the reaction force at the
support.
Solution
(a) Using two elements, each of 0.3m in length, we
obtain the finite element model in Figure 1a. In this
model, 0)1(
1 =x , 3.0)1(
2 =x , 3.0)2(
1 =x , 6.0)2(
2 =x ,
and A(x)=0.0012-0.001x .
(b) For element 1, [ ]xx−= 3.0
3.0
1
N(1)
,
[ ]11
3.0
1
B(1)
−= , the element stiffness matrix is
,
7.07.0
7.07.0
10
11
11
)001.00012.0(
09.0
10200
BBK
9
3.0
0
9
3.0
0
)1((1)T(1)
−
−
=
−
−
−
×
=
=
∫
∫
dxx
dxAE
the element body force vector is
( )
+
−
−−×
=
+=
∫
∫ =
100
0
)001.00012.0(
)001.00012.0)(3.0(
3.0
107
NNf
3.0
0
3
3.0
(1)T
3.0
0
(1)T(1)
dx
xx
xx
PAdx
x
ρ
=
05.101
155.1
, and the scatter matrix is
=
010
001
L(1)
.](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Recommended
Recommended
More Related Content
What's hot
What's hot (20)
Similar to Solution homework2
Similar to Solution homework2 (20)
Recently uploaded
Recently uploaded (20)
Solution homework2
- 1. 1 ES 128: Homework 2 Solutions Problem 1 Show that the weak form of 02)( =+ x dx du AE dx d on 31 << x , 1.0)1( 1 = = =xdx du Eσ , 001.0)3( =u is given by ∫∫ +−= = 3 1 1 3 1 2)(1.0 xwdxwAdx dx du AE dx dw x w∀ with 0)3( =w . Solution We multiply the governing equation and the natural boundary condition over the domain [1, 3] by an arbitrary weight function: 02 3 1 = + ∫ dxx dx du AE dx d w )(xw∀ , (1.1) 01.0 1 = − =x dx du EwA )1(w∀ . (1.2) We integrate (1.1) by parts as dx dx du AE dx dw dx du wAEdx dx du AE dx d w x x ∫∫ − = = = 3 1 3 1 3 1 . (1.3) Substituting (1.3) into (1.1) gives 02 13 3 1 3 1 = − ++ − == ∫∫ xx dx du wAE dx du wAEwxdxdx dx du AE dx dw )(xw∀ . (1.4) With 0)3( =w and 1.0)1( =σ , we obtain ( ) 1 3 1 3 1 1.02 = −= ∫∫ x wAwxdxdx dx du AE dx dw )(xw∀ with 0)3( =w . (1.5)
- 2. 2 El (1) El (2) 1 2 3 Figure 1a x Problem 2 Consider the (steel) bar in Figure 1. The bar has a uniform thickness t=1cm, Young’s modulus E=200 9 10× Pa, and weight density ρ =7 3 10× 3 /mkg . In addition to its self-weight, the bar is subjected to a point load P=100N at its midpoint. (a) Model the bar with two finite elements. (b) Write down expressions for the element stiffness matrices and element body force vectors. (c) Assemble the structural stiffness matrix K and global load vector F . (d) Solve for the global displacement vector d. (e) Evaluate the stresses in each element. (f) Determine the reaction force at the support. Solution (a) Using two elements, each of 0.3m in length, we obtain the finite element model in Figure 1a. In this model, 0)1( 1 =x , 3.0)1( 2 =x , 3.0)2( 1 =x , 6.0)2( 2 =x , and A(x)=0.0012-0.001x . (b) For element 1, [ ]xx−= 3.0 3.0 1 N(1) , [ ]11 3.0 1 B(1) −= , the element stiffness matrix is , 7.07.0 7.07.0 10 11 11 )001.00012.0( 09.0 10200 BBK 9 3.0 0 9 3.0 0 )1((1)T(1) − − = − − − × = = ∫ ∫ dxx dxAE the element body force vector is ( ) + − −−× = += ∫ ∫ = 100 0 )001.00012.0( )001.00012.0)(3.0( 3.0 107 NNf 3.0 0 3 3.0 (1)T 3.0 0 (1)T(1) dx xx xx PAdx x ρ = 05.101 155.1 , and the scatter matrix is = 010 001 L(1) .
- 3. 3 For element 2, [ ]3.06.0 3.0 1 N(2) −−= xx , [ ]11 3.0 1 B(2) −= , the element stiffness matrix is dxxdxAE ∫∫ − − − × == 6.0 3.0 9 6.0 3.0 )2((2)T(2) 11 11 )001.00012.0( 09.0 10200 BBK , 5.05.0 5.05.0 109 − − = the element body force vector is dx xx xx Adx ∫∫ −− −−× == 6.0 3.0 3 6.0 3.0 (2)T(2) )001.00012.0)(3.0( )001.00012.0)(6.0( 3.0 107 Nf ρ = 735.0 84.0 , and the scatter matrix is = 100 010 L(2) . (c) The global stiffness matrix is =+== ∑= (2)(2)(2)T(1)(1)(1)T 2 1e eeeT LKLLKLLKLK − −− − 5.05.00 5.02.17.0 07.07.0 109 . The global load vector is =+== ∑= (2)(2)T(1)(1)T 2 1e eeT fLfLfLf 735.0 89.101 155.1 . (d) Note that only the reaction force at node 1 is not zero, thus + =+ 735.0 89.101 155.1 rf 1r . The resulting global system of equations is − −− − 5.05.00 5.02.17.0 07.07.0 109 3 2 0 u u = + 735.0 89.101 155.11r . Solving the above equation, 2u = 1.46607 7_ 10× (m), 3u = 1.48077 7_ 10× (m), and 1r =-103.78(N). (e) The stress field in element 1 is given by × −××== −7 9(1)(1))1( 1046607.1 0 ]11[ 3.0 1 10200dB)( Exσ =9.7738 4 10× (Pa). The stress field in element 2 is given by × × −××== − − 7 7 9(2)(2))2( 1048077.1 1046607.1 ]11[ 3.0 1 10200dB)( Exσ =980 (Pa). (f) The reaction force at the support Node 1 is -103.78N.
- 4. 4 Problem 3 Consider the mesh shown in Figure 2. The model consists of two linear displacement constant strain elements. The cross-sectional area is A=1, Young’s modulus is E; both are constant. A body force b(x)=cx is applied. (a) Solve and plot u(x) and )(xε for the FEM solution. (b) Compare (by plotting) the finite element solution against the exact solution for the equation .)(2 2 cxxb dx ud E −=−= (c) Solve the above problem using a single quadratic displacement element. (d) Compare the accuracy of stress and displacement at the right end with that of two linear displacement elements. (e) Check whether the equilibrium equation and traction boundary condition are satisfied for the two meshes. Solution (a) Using two linear displacement constant strain elements, each of l in length, we obtain the finite element model with 0)1( 1 =x , lx =)1( 2 , lx =)2( 1 , and lx 2)2( 2 = . For element 1, [ ]xxl l −= 1 N(1) , [ ]11 1 B(1) −= l , the element stiffness matrix is − − = 11 11 K(1) l EA , the element body force vector is == ∫ 3/ 6/ Nf 2 2 0 (1)T(1) cl cl cxdx l , and the scatter matrix is = 010 001 L(1) . For element 2, [ ]lxxl l −−= 2 1 N(2) , [ ]11 1 B(2) −= l , the element stiffness matrix is − − = 11 11 K(2) l EA , the element body force vector is == ∫ 6/5 3/2 Nf 2 2 2 (2)T(2) cl cl cxdx l l , and the scatter matrix is = 100 010 L(2) . The global stiffness matrix is =+== ∑= (2)(2)(2)T(1)(1)(1)T 2 1e eeeT LKLLKLLKLK − −− − 110 121 011 l EA . The global load vector is Figure 2
- 5. 5 =+== ∑= (2)(2)T(1)(1)T 2 1e eeT fLfLfLf 8333.0 0.1 1667.0 2 cl . The resulting global system of equations is − −− − 110 121 011 l EA 3 2 0 u u = + 2 2 2 1 8333.0 1667.0 cl cl clr . Solving the above equation, 2u = 1.8333 EA cl3 , 3u = 2.6666 EA cl3 , and 1r =-2 2 cl . When lx ≤≤0 [ ] EA xcl EA clxxl l xu 2 3(1)(1) 8333.1 8333.1 01 dN)( = −== , and EA cl dx du x 2 8333.1)( ==ε . When lxl 2≤≤ [ ] x EA cl EA cl EA cl EA cl lxxl l xu 23 3 3 (2)(2) 8333.0 6666.2 8333.1 2 1 dN)( += −−== , and EA cl dx du x 2 8333.0)( ==ε . (b). The governing equation is ,)(2 2 cxxb dx ud EA −=−= where A=1. The boundary condition is u(0)=0, and 0)2( =lσ . Solving this linear ODE, we obtain the exact solution 21 3 6 )( cxcx EA c xu ++−= . Since u(0)=0, 02 =c . Since 0)2( =lσ , EA cl c 2 1 2 = . Thus x EA cl x EA c xu 2 3 2 6 )( +−= . 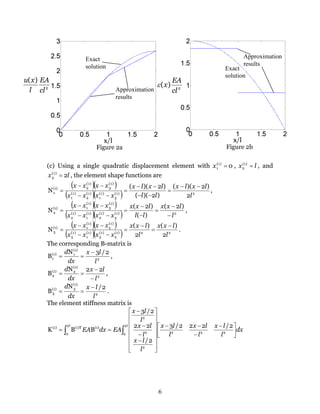EA cl EA cx x 22 2 2 )( +−=ε The comparisons between the approximation results and the exact solutions are shown in Figures 2a (displacement), and 2b (strain).
- 6. 6 2 )( cl EA l xu 2 )( cl EA xε Exact solution Exact solution Approximation results Approximation results Figure 2a Figure 2b (c) Using a single quadratic displacement element with 0)1( 1 =x , lx =)1( 2 , and lx 2)1( 3 = , the element shape functions are ( )( ) ( )( ) 2)1( 3 )1( 1 )1( 2 )1( 1 )1( 3 )1( 2(1) 1 2 )2)(( )2)(( )2)(( N l lxlx ll lxlx xxxx xxxx −− = −− −− = −− −− = , ( )( ) ( )( ) 2)1( 3 )1( 2 )1( 1 )1( 2 )1( 3 )1( 1(1) 2 )2( )( )2( N l lxx ll lxx xxxx xxxx − − = − − = −− −− = , ( )( ) ( )( ) 22)1( 2 )1( 3 )1( 1 )1( 3 )1( 2 )1( 1(1) 3 2 )( 2 )( N l lxx l lxx xxxx xxxx − = − = −− −− = . The corresponding B-matrix is 2 (1) 1(1) 1 2/3N B l lx dx d − == , 2 (1) 2(1) 2 22N B l lx dx d − − == , 2 (1) 3(1) 3 2/N B l lx dx d − == . The element stiffness matrix is dx l lx l lx l lx l lx l lx l lx EAdxEA ll − − −− − − − − == ∫∫ 222 2 2 2 2 2 2 0 (1)(1)T(1) 2/222/3 2/ 22 2/3 BBK
- 7. 7 dx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx l lx EA l ∫ − − − − − − − − − − − − − − − − − − − − = 2 0 22222 22 2 222 2222 2 2 2/2/222/2/3 2/2222222/3 2/2/3222/32/3 . 6/73/46/1 3/43/83/4 6/13/46/7 − −− − = l EA The element body force vector is == ∫ 3/2 3/4 0 Nf 2 2 2 0 (1)T(1) cl clcxdx l . The resulting global system of equations is − −− − 6/73/46/1 3/43/83/4 6/13/46/7 l EA 3 2 0 u u = 3/2 3/4 2 2 1 cl cl r . Solving the above equation, we obtain 2u = 1.8333 EA cl3 , 3u = 2.6666 EA cl3 , and 1r =-2 2 cl . − − −−− == EA cl EA cl l lxx l lxx l lxlx xu 3 3 222 (1)(1) 6666.2 8333.1 0 2 )()2( 2 )2)(( dN)( , x EA cl x EA cl 2 2 3333.2 5.0 +−= . EA cl x EA cl x 2 3333.2)( +−=ε . (d) At the right end with x=2l, for both of two linear displacement elements and a single quadratic displacement element, the displacements are same to the exact result ( 3u = 2.6666 EA cl3 ). As for the stress and strain, with two linear displacement elements, we obtain EA cl l 2 8333.0)2( =ε and A cl l 2 8333.0)2( =σ .
- 8. 8 With a single quadratic displacement element, EA cl l 2 3333.0)2( =ε , and A cl l 2 3333.0)2( =σ . It is found that the approximation result of the stress and strain with a single quadratic displacement element is closer to the exact result ( 0=σ and 0=ε ). (e). For both of two linear displacement elements and a single quadratic displacement element, the reaction forces acting on node 1 are 1r =-2 2 cl , which satisfy the equilibrium equation ( 0 2 0 1 =+ ∫ l cxdxr ). However, as shown in (d), the stress boundary conditions are not satisfied for the two meshes.