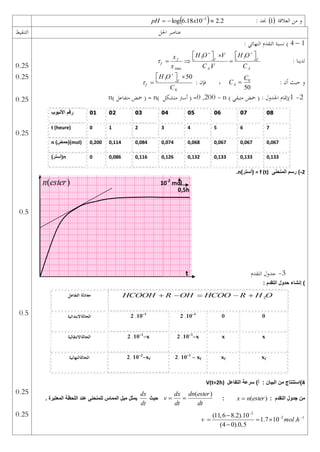
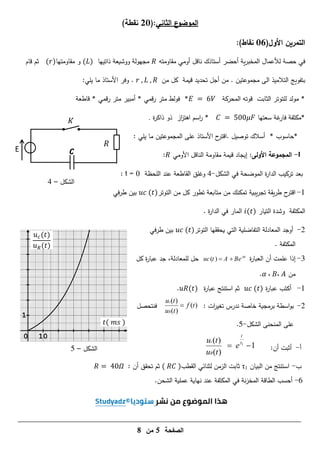
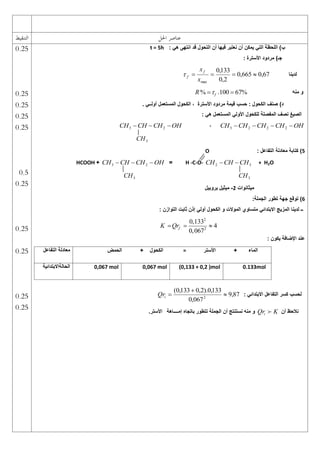
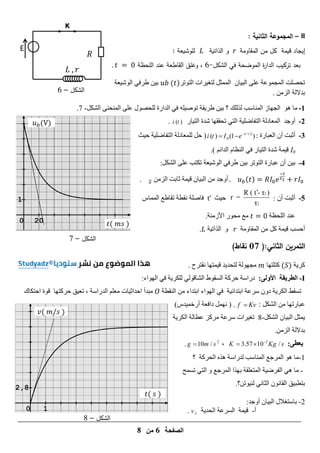
The document provides information and questions related to physics concepts including: 1) Kinematics equations and graphs describing the motion of an object projected at an angle. 2) Conservation of energy applied to calculate velocities. 3) Radioactive decay described through equations and graphs of activity over time.

1. ‫الصفحة‬
1
‫من‬
8
‫أ‬ ‫البيان‬
0 0,25
1
𝑡 ( 𝑠 )
𝑥 ( 𝑚 )
0 0,2
2
𝑡 ( 𝑠 )
𝑣𝑦 ( 𝑚. 𝑠−1
)
‫ب‬ ‫البيان‬
‫الشعبيـة‬ ‫اطيـة‬
‫ر‬‫الديـمق‬ ‫ائريـة‬
‫ز‬‫الـج‬ ‫الـجمهوريـة‬
‫الية‬‫و‬‫ل‬ ‫التربية‬ ‫مديرية‬
–
‫سطيف‬
-
‫الوطنيـة‬ ‫التربية‬ ‫ة‬
‫ار‬
‫ز‬‫و‬
‫ا‬ ‫البكالوريـا‬ ‫امتحان‬
‫لتجريبيـة‬
‫سطيف‬ ‫ثانويـات‬
‫ال‬
‫مقاطعة‬
11
:‫الشعبة‬
‫تجريبية‬ ‫عموم‬
‫ة‬
‫دور‬
‫ماي‬
7117
‫اخت‬
‫ب‬
‫في‬ ‫ــار‬
‫م‬
‫الع‬ :‫ادة‬
‫م‬
‫الفيزيائي‬ ‫وم‬
‫ـة‬
:‫الـمـــدة‬
13
‫ساعات‬
‫ونصف‬
‫الـموضوعين‬ ‫أحد‬ ‫يختار‬ ‫أن‬ ‫الـمترشح‬ ‫عمى‬
:‫اليين‬ّ
‫ت‬‫ال‬
‫األول‬ ‫ع‬
‫الموضو‬
(:
71
)‫نقطة‬
‫ا‬ ‫التمرين‬
‫ألول‬
(
16
)‫نقاط‬
:
1
-
‫جسما‬ ‫نقذف‬
(s)
‫نقطة‬ ‫من‬ ‫مادية‬ ‫نقطة‬ ‫ه‬
‫ر‬‫نعتب‬
A
‫اوية‬
‫ز‬‫ب‬ ‫األفق‬ ‫عن‬ ‫يميل‬ ‫أممس‬ ‫مستوي‬ ‫أسفل‬ ‫تقع‬
𝛼
‫الميل‬ ‫خط‬ ‫وفق‬
‫األعظمي‬
‫عة‬
‫بسر‬
‫النقطة‬ ‫إلى‬ ‫فيصل‬
‫ىا‬
‫قدر‬ ‫عة‬
‫بسر‬
‫الشكل‬ ‫في‬ ‫مبين‬ ‫ىو‬ ‫كما‬
–
1
.
‫أ‬
-
‫الجسم‬ ‫عمى‬ ‫ة‬
‫ر‬‫المؤث‬ ‫القوى‬ ‫ل‬ّ‫ث‬‫م‬
( )
.
‫ب‬
-
‫الجسم‬ ‫عمى‬ ‫لنيوتن‬ ‫الثاني‬ ‫ن‬‫القانو‬ ‫بتطبيق‬
( )
‫المسار‬ ‫عمى‬ ‫الحركة‬ ‫ع‬
‫تسار‬ ‫ة‬
‫ر‬‫عبا‬ ‫أوجد‬
.
‫ـ‬‫ج‬
-
‫المسار‬ ‫عمى‬ ‫الحركة‬ ‫طبيعة‬ ‫ما‬
.‫إجابتك‬ ‫؟عمل‬
2
–
‫النقطة‬ ‫بعد‬ ‫الجسم‬ ‫حركة‬
‫البيان‬ ‫يمثل‬
(
‫أ‬
)
‫فاصمة‬ ‫ات‬
‫ر‬‫تغي‬
‫البيان‬ ‫يمثل‬ ‫و‬ ،‫الزمن‬ ‫بداللة‬ ‫القذيفة‬
(
‫ب‬
)
‫ات‬
‫ر‬‫تغي‬
‫المركبة‬
‫ل‬
‫القذيفة‬ ‫عة‬
‫سر‬
.
‫عمى‬
‫ال‬
‫محور‬
:‫الزمن‬ ‫بداللة‬
‫أ‬
-
‫بالبيانين‬ ‫مستعينا‬
( ) ‫أ‬
‫و‬
() ‫ب‬
‫استنتج‬
‫و‬
‫شعاع‬ ‫مركبتي‬
‫عة‬
‫السر‬
‫أحسب‬ ‫ثم‬ ،
.‫طويمتو‬ 𝑣0
1 − ‫الشكل‬
𝑌
ℎ
𝑣0
𝑆
𝛼
𝐴
𝐻
𝑋
𝑂

2. ‫الصفحة‬
7
‫من‬
8
‫ب‬
-
‫اوية‬
‫ز‬‫ال‬ ‫قيمة‬ ‫أحسب‬
𝛼
.
3
-
‫عة‬
‫سر‬ ‫أحسب‬ ،)‫أرض‬+‫(جسم‬ ‫الجممة‬ ‫عمى‬ ‫الطاقة‬ ‫انحفاظ‬ ‫مبدأ‬ ‫بتطبيق‬
‫الجسم‬
‫عند‬
‫الموضع‬
‫أن‬ ‫عمما‬
1
4
-
‫الجسم‬ ‫فييا‬ ‫يصل‬ ‫التي‬ ‫حظة‬ّ
‫م‬‫ال‬ ‫باعتبار‬
( )
‫الموضع‬ ‫إلى‬
‫لألزمنة‬ ‫مبدأ‬
،
‫بإىمال‬ ‫و‬
‫تأثير‬
‫اء‬‫و‬‫الي‬
.
‫أ‬
-
ٌ‫اىجس‬ ‫ػطاىح‬ ‫ٍسمص‬ ‫ٍساز‬ ‫ٍؼادىح‬ ‫أٗجد‬
( )
ٌ‫اىَؼي‬ ٜ‫ف‬
(O ; OX ; OY)
.
‫ب‬
-
‫اىْقطح‬ ‫تؼد‬ ‫ّد‬‫د‬‫د‬
f
‫اىْقطح‬ ِ‫ػ‬
.)‫فح‬ٝ‫ىيقر‬ ٜ‫األفق‬ ٙ‫(اىَد‬
‫جـ‬
-
‫اىْقط‬ ٜٞ‫إدداث‬ ‫أٗجد‬
‫ح‬
‫تاألزض‬ ‫فح‬ٝ‫اىقر‬ ً‫اصطدا‬ ‫ّقطح‬
:‫يعطى‬
1 . −
‫ا‬ ‫التمرين‬
‫لثاني‬
(
17
)‫نقاط‬
:
‫االختصاصات‬ ‫أىم‬ ‫من‬ ‫النووي‬ ‫الطب‬ ‫يعتبر‬
،
‫المعتمدة‬ ‫التقنيات‬ ‫بين‬ ‫من‬ .‫عالجيا‬ ‫وفي‬ ‫اض‬
‫ر‬‫األم‬ ‫تشخيص‬ ‫في‬ ‫يستعمل‬ ‫إذ‬
radiothérapie)
)
‫باإلشعاع‬ ‫المصاب‬ ‫النسيج‬ ‫أو‬ ‫الورم‬ ‫يقذف‬ ‫إذ‬ ‫السرطانية‬ ‫ام‬
‫ر‬‫األو‬ ‫تدمير‬ ‫في‬ ‫النووي‬ ‫اإلشعاع‬ ‫يستعمل‬ ‫حيث‬
‫الكوبالت‬ ‫من‬ ‫المنبعث‬
0
.
‫ـ‬‫ل‬ ‫اإلشعاعي‬ ‫النشاط‬ ‫يفسر‬
‫ن‬‫نترو‬ ‫بتحول‬
‫بر‬ ‫إلى‬
‫ن‬‫وتو‬
‫الشكل‬ ‫منحنى‬ ‫يمثل‬.
-
‫ات‬
‫ر‬‫تغي‬
‫ال‬
‫نشاط‬
‫ل‬
‫عينة‬
‫بداللة‬ ‫الكوبالت‬ ‫من‬
‫الزمن‬ ‫خالل‬ ‫المتفككة‬ ‫األنوية‬ ‫عدد‬
.
1
-
‫أ‬
-
‫التعميل؟‬ ‫مع‬ ‫لمكوبالت‬ ‫اإلشعاعي‬ ‫النشاط‬ ‫نمط‬ ‫حدد‬
‫ب‬
-
‫التفاعل‬ ‫معادلة‬ ‫اكتب‬
‫ثم‬ ‫افق‬‫و‬‫الم‬ ‫النووي‬
‫اة‬‫و‬‫الن‬ ‫عمى‬ ‫تعرف‬
‫االبن‬
‫اتين‬‫و‬‫الن‬ ‫بين‬ ‫من‬
28Ni
,
26Fe
.
‫ت‬
-
‫اإلشعاعي‬ ‫التناقص‬ ‫ن‬‫قانو‬ ‫اكتب‬
‫ثم‬ ،
‫ية‬‫ر‬‫النظ‬ ‫العالقة‬
‫بط‬‫ر‬‫ت‬ ‫التي‬
‫اإلشعاعي‬ ‫النشاط‬
‫ب‬
‫األنوية‬ ‫عدد‬
. ‫المتفككة‬
2
-
:‫حدد‬ ‫ن‬ ‫البيا‬ ‫باستغالل‬
‫أ‬
-
‫االبتدائي‬ ‫اإلشعاعي‬ ‫النشاط‬
‫لمعينة‬
.
‫ب‬
-
‫اإلشعاعي‬ ‫النشاط‬ ‫ثابت‬
λ
‫الكوبالت‬ ‫اة‬‫و‬‫لن‬
66
.
‫ـ‬‫ج‬
-
‫االبتدائية‬ ‫األنوية‬ ‫عدد‬
‫كتمتيا‬ ‫و‬ ‫لمعينة‬
.
3
-
‫النسبة‬ ‫اصبحت‬ ‫إذا‬ ‫لالستعمال‬ ‫صالحة‬ ‫غير‬ ‫العينة‬ ‫اعتبار‬ ‫يمكن‬
N
3
N


‫حيث‬
N
. ‫المتبقية‬ ‫األنوية‬ ‫عدد‬
‫أ‬
-
‫النسبة‬ ‫كتابة‬ ‫يمكن‬ ‫أنو‬ ‫بين‬
N
N

‫التالية‬ ‫بالعالقة‬
t
N
(e 1)
N


 
‫ب‬
-
‫التي‬ ‫الزمنية‬ ‫المدة‬ ‫استنتج‬
‫اعتبار‬ ‫فييا‬ ‫يمكن‬
‫غير‬ ‫العينة‬
.‫لالستعمال‬ ‫صالحة‬
‫الشكل‬
-
2
0 0,5
2
𝐴 × 1 13
(𝐵𝑞)
𝑁 × 1

3. ‫الصفحة‬
3
‫من‬
8
(:‫التجريبي‬ ‫التمرين‬
17
)‫نقاط‬
:‫إلى‬ ‫ين‬‫ر‬‫التم‬ ‫ىذا‬ ‫ييدف‬
‫و‬ ‫كيميائي‬ ‫لتحول‬ ‫الزمنية‬ ‫المتابعة‬
.‫ي‬
‫تجار‬ ‫محمول‬ ‫ة‬
‫ر‬‫معاي‬
‫مالحظة‬
:

‫الدرجة‬ ‫في‬ ‫مأخوذة‬ ‫المائية‬ ‫المحاليل‬ ‫كل‬
.

: ‫يوم‬‫ز‬‫المغني‬ ‫لمعدن‬ ‫المولية‬ ‫الكتمة‬
. −1
.

: ‫لمماء‬ ‫الشاردي‬ ‫الجداء‬
1 −1
.
I
-
.‫المغنيزيوم‬ ‫ومعدن‬ ‫الماء‬ ‫كمور‬ ‫حمض‬ ‫بين‬ ‫الحادث‬ ‫الكيميائي‬ ‫لمتحول‬ ‫الزمنية‬ ‫المتابعة‬
‫حجما‬ ‫بيشر‬ ‫في‬ ‫نضع‬
‫محمول‬ ‫من‬
( )
‫الماء‬ ‫كمور‬ ‫لحمض‬
( 3 ( ) −
( ) )
‫ه‬
‫ز‬‫تركي‬
‫المولي‬
‫ـ‬‫ل‬‫ا‬ ‫مقياس‬ ‫ى‬
‫مسر‬ ‫فيو‬ ‫وندخل‬ ،
.
‫عند‬
‫المحظة‬
‫يوم‬‫ز‬‫المغني‬ ‫ق‬‫مسحو‬ ‫من‬ ‫كمية‬ ‫البيشر‬ ‫إلى‬ ‫نضيف‬ ،
( )
‫كتمتيا‬
‫تحول‬ ‫فيحدث‬ ،
‫ينمذج‬ ‫كيميائي‬
‫بتفاعل‬
‫معادل‬
‫تو‬
:
3 ( ) ( ) ( ) ( ) ( )
‫تام‬ ‫التحول‬ ‫ىذا‬ ‫يعتبر‬
‫الكيميائية‬ ‫الجممة‬ ‫حجم‬ ‫نعتبر‬.
.
1
-
‫حمض‬ ( ‫لمجممة‬ ‫الحادث‬ ‫التحول‬ ‫أن‬ ‫بين‬
-
‫ة‬
‫ر‬‫عبا‬ )‫معدن‬
‫عن‬
‫أكسدة‬ ‫تفاعل‬
-
‫إرجاع‬
‫المشاركتان‬ ‫الثنائيتان‬ ‫تحديد‬ ‫مع‬
.‫التفاعل‬ ‫في‬
2
-
‫تطور‬ ‫متابعة‬ ‫نتائج‬
‫المحمول‬
‫زمنية‬ ‫ت‬ ‫لحظا‬ ‫خالل‬
‫ك‬
‫ا‬
‫كما‬ ‫نت‬
:‫التالي‬ ‫الجدول‬ ‫في‬
1
1
1
1
( )
2
-
1
-
‫المولي‬ ‫التركيز‬ ‫استنتج‬
.‫المستعمل‬ ‫الماء‬ ‫كمور‬ ‫حمض‬ ‫لمحمول‬
2
-
2
-
‫األعظمي‬ ‫التقدم‬ ‫أحسب‬
‫حدد‬ ‫ثم‬
. ‫المحد‬ ‫المتفاعل‬
2
-
3
-
‫التقدم‬ ‫ة‬
‫ر‬‫عبا‬ ‫أن‬ ‫بين‬
( )
‫في‬ ‫لمتفاعل‬
‫لحظة‬
:‫الشكل‬ ‫عمى‬ ‫تكتب‬
( )
1
( − 1 − )
.
2
-
4
-
.‫تام‬ ‫التحول‬ ‫ىذا‬ ‫أن‬ ‫فعال‬ ‫تأكد‬
2
-
5
-
‫التفاعل‬ ‫نصف‬ ‫زمن‬ ‫حدد‬
1
.
2
-
6
-
‫أح‬
‫لمتفاعل‬ ‫الحجمية‬ ‫المتوسطة‬ ‫عة‬
‫السر‬ ‫سب‬
.
:‫المحظتين‬ ‫بين‬
1 1
‫و‬
.
II
-
‫لألمونياك‬ ‫ي‬
‫التجار‬ ‫المحمول‬ ‫ة‬
‫معاير‬
.
‫ي‬
‫تجار‬ ‫محمول‬ ‫عمى‬ ‫نتوفر‬
‫األمونياك‬ ‫من‬
3
‫المولي‬ ‫ه‬
‫ز‬‫تركي‬
‫الة‬
‫ز‬‫إل‬ ‫كمادة‬ ‫أو‬ ‫لمتنظيف‬ ‫كمادة‬ ‫تخفيفو‬ ‫بعد‬ ‫يستعمل‬ ،
‫لتعيين‬ . ‫البقع‬
‫ال‬
‫تركيز‬
‫ل‬
‫نمدده‬ ، ‫المحمول‬ ‫يذا‬
1
‫فن‬ ، ‫ة‬
‫ر‬‫م‬
‫ت‬
‫محمول‬ ‫عمى‬ ‫حصل‬
1
‫المولي‬ ‫ه‬
‫ز‬‫تركي‬
1
.

4. ‫الصفحة‬
4
‫من‬
8
2
1
𝑉
𝑎(𝑚𝐿)
‫الشكل‬
-
3
‫ة‬
‫ر‬‫معاي‬ ‫ي‬
‫نجر‬
‫لحجم‬ ‫ية‬‫ر‬‫مت‬
1
‫المحمول‬ ‫من‬
1
‫بمحمول‬
‫الماء‬ ‫كمور‬ ‫لحمض‬
( 3 ( ) −
( ) )
‫المولي‬ ‫ه‬
‫ز‬‫تركي‬
. 1 −
. −1
‫المحمول‬ ‫من‬ ‫عميو‬ ‫المتحصل‬‫و‬
‫تمديده‬ ‫بعد‬
‫الشكل‬ ‫في‬ ‫الممثل‬ ‫البيان‬ ‫عمى‬ ‫فنحصل‬ ، ‫ة‬
‫ر‬‫م‬
-
3
.
1
-
‫أكتب‬
‫معادلة‬
‫المنمذج‬ ‫التفاعل‬
‫ل‬
‫م‬
‫تحول‬
.‫ة‬
‫ر‬‫معاي‬
2
-
‫أ‬
-
‫استنتج‬ ‫ثم‬ ‫التكافؤ‬ ‫نقطة‬ ‫عرف‬
‫إحداثي‬
‫ي‬
.‫يا‬
‫ب‬
-
‫المولي‬ ‫التركيز‬ ‫أحسب‬
1
‫لممحمول‬
1
‫ثم‬
‫المولي‬ ‫التركيز‬ ‫استنتج‬
‫لممحمول‬
.
‫ج‬
-
‫؟‬ ‫ذلك‬ ‫تفسر‬ ‫كيف‬ ‫؟‬ ‫الناتج‬ ‫المحمول‬ ‫طبيعة‬ ‫ما‬
3
-
‫أ‬
-
‫قيمة‬ ‫البيان‬ ‫من‬ ‫أوجد‬
‫ـ‬‫ل‬‫ا‬
‫أجل‬ ‫من‬
.
‫أ‬
-
‫باالعتماد‬
.‫تام‬ ‫تحول‬ ‫ة‬
‫ر‬‫المعاي‬ ‫تفاعل‬ ّ
‫أن‬ ‫ن‬ّ
‫بي‬ ،‫القيمة‬ ‫ىذه‬ ‫عمى‬
‫ا‬
‫ن‬
‫األول‬ ‫ع‬
‫الموضو‬ ‫تهى‬

5. ‫الصفحة‬
5
‫من‬
8
𝑅
E
‫الشكل‬
–
4
𝐾
0 10
1
𝑡( 𝑚𝑠 )
𝑢𝑐(𝑡)
𝑢𝑅(𝑡)
‫الشكل‬
–
5
)‫نقطة‬ 71(:‫الثاني‬ ‫ع‬
‫الموضو‬
‫ا‬ ‫التمرين‬
‫ألول‬
(
16
)‫نقاط‬
:
‫مقاومتو‬ ‫أومي‬ ‫ناقل‬ ‫أستاذك‬ ‫أحضر‬ ‫ية‬‫ر‬‫المخب‬ ‫لألعمال‬ ‫حصة‬ ‫في‬
‫ووشيعة‬ ‫مجيولة‬
‫ذاتييا‬
( )
‫مقاومتيا‬ ‫و‬
( )
‫قام‬ ‫ثم‬
‫بتفويج‬
‫مجموعتين‬ ‫الى‬ ‫التالميذ‬
.
‫أجل‬ ‫من‬
‫تحديد‬
‫قيمة‬
‫من‬ ‫كل‬
.
‫وفر‬
‫األستاذ‬
‫يمي‬ ‫ما‬
:
‫مولد‬ *
‫لمتوتر‬
‫الثابت‬
‫المحركة‬ ‫قوتو‬
*
‫قمي‬‫ر‬ ‫متر‬ ‫أمبير‬ * ‫قمي‬‫ر‬ ‫متر‬ ‫فولط‬
‫قاطعة‬ *
‫سعتيا‬ ‫غة‬
‫فار‬ ‫*مكثفة‬
*
‫اسم‬
‫ر‬
‫از‬
‫ز‬‫اىت‬
‫ة‬
‫ر‬‫ذاك‬ ‫ذو‬
.
* ‫*حاسوب‬
‫توصيل‬ ‫أسالك‬
.
‫ح‬
‫اقتر‬
‫األستاذ‬
: ‫يمي‬ ‫ما‬ ‫المجموعتين‬ ‫عمى‬
I
-
‫األولى‬ ‫المجموعة‬
:
‫األومي‬ ‫الناقل‬ ‫مقاومة‬ ‫قيمة‬ ‫إيجاد‬
:
‫بعد‬
‫الشكل‬ ‫في‬ ‫الموضحة‬ ‫ة‬
‫ر‬‫الدا‬ ‫تركيب‬
-
4
‫و‬
‫عند‬ ‫القاطعة‬ ‫غمق‬
‫المحظة‬
t = 0
:
1
-
‫ح‬
‫اقتر‬
‫التوتر‬ ‫من‬ ‫كل‬ ‫تطور‬ ‫متابعة‬ ‫من‬ ‫تمكنك‬ ‫يبية‬‫ر‬‫تج‬ ‫يقة‬‫ر‬‫ط‬
( )
‫في‬‫ر‬‫ط‬ ‫بين‬
‫المكثفة‬
‫و‬
‫شدة‬
‫التيار‬
( )
‫ة‬
‫ر‬‫الدا‬ ‫في‬ ‫المار‬
.
2
-
‫أو‬
‫التوتر‬ ‫يحققيا‬ ‫التي‬ ‫التفاضمية‬ ‫المعادلة‬ ‫جد‬
( )
‫في‬‫ر‬‫ط‬ ‫بين‬
‫المكثفة‬
.
3
-
‫أن‬ ‫عممت‬ ‫إذا‬
‫ة‬
‫ر‬‫العبا‬
( ) t
uc t A Be
 
‫كل‬ ‫ة‬
‫ر‬‫عبا‬ ‫جد‬ ،‫لممعادلة‬ ‫حل‬
‫من‬
𝛼 ، ،
.
1
-
‫ة‬
‫ر‬‫عبا‬ ‫أكتب‬
( )
‫ثم‬
‫استنتج‬
‫ة‬
‫ر‬‫عبا‬
( )
.
2
-
: ‫ات‬
‫ر‬‫تغي‬ ‫ندرس‬ ‫خاصة‬ ‫برمجية‬ ‫اسطة‬‫و‬‫ب‬
( )
( )
( )
c
R
u t
f t
u t

‫فنتحصل‬
‫المنحنى‬ ‫عمى‬
‫الشكل‬
-
5
.
‫أ‬
-
:‫أن‬ ‫أثبت‬
1
( )
1
( )
c
R
t
u t
e
u t

 
‫ب‬
-
‫البيان‬ ‫من‬ ‫استنتج‬
1
τ
‫ثابت‬
‫الزمن‬
‫لثنائي‬
‫القطب‬
( )
: ‫أن‬ ‫تحقق‬ ‫ثم‬
𝛺
6
-
‫المكثفة‬ ‫في‬ ‫نة‬‫ز‬‫المخ‬ ‫الطاقة‬ ‫أحسب‬
‫عممية‬ ‫نياية‬ ‫عند‬
.‫الشحن‬

6. ‫الصفحة‬
6
‫من‬
8
𝑅
E
‫الشكل‬
–
6
𝐿 𝑟
0 20
1
𝑡( 𝑚𝑠 )
𝑢𝑏(V)
‫الشكل‬
–
7
0 1
2,8
𝑡( 𝑠 )
𝑣( 𝑚 𝑠 )
‫الشكل‬
–
8
II
–
: ‫الثانية‬ ‫المجموعة‬
‫إيجاد‬
‫قيمة‬
‫كل‬
‫من‬
‫المقاومة‬
‫الذاتية‬ ‫و‬
‫لموشيعة‬
:
‫بعد‬
‫الشكل‬ ‫في‬ ‫الموضحة‬ ‫ة‬
‫ر‬‫الدا‬ ‫تركيب‬
-
6
،
‫و‬
‫القاطعة‬ ‫غمق‬
‫المحظة‬ ‫عند‬
.
ُ‫ا‬ٞ‫اىث‬ ٚ‫ػي‬ ‫اىَجَ٘ػح‬ ‫ذذصيد‬
‫اىر٘ذس‬ ‫ساخ‬ٞ‫ىرغ‬ ‫اىََثو‬
( )
‫ؼح‬ٞ‫اى٘ش‬ ٜ‫طسف‬ ِٞ‫ت‬
ٍِ‫اىص‬ ‫تدالىح‬
.
1
-
‫اىجٖاش‬ ٕ٘ ‫ٍا‬
‫ىرىيل‬ ‫اىَْاسة‬
‫ذ‬ ‫قح‬ٝ‫طس‬ ِٞ‫ت‬ ‫؟‬
‫اىدازج‬ ٜ‫ف‬ ٔ‫ي‬ٞ‫٘ص‬
ْ‫اىَْذ‬ ٚ‫ػي‬ ‫ىيذص٘ه‬
ٚ
‫اىشنو‬
-
7
.
2
-
‫أٗجد‬
ٜ‫اىر‬ ‫ح‬ٞ‫اىرفاظي‬ ‫اىَؼادىح‬
‫ذ‬
‫از‬ٞ‫اىر‬ ‫شدج‬ ‫ذققٖا‬
( )
i t
.
3
-
ُ‫أ‬ ‫أثثد‬
‫اىؼثازج‬
:
/ 2
0
( ) (1 )
t
i t I e 

 
)
‫ث‬ٞ‫د‬ ‫ح‬ٞ‫اىرفاظي‬ ‫ىيَؼادىح‬ ‫دو‬
I0
‫َح‬ٞ‫ق‬
‫شدج‬
ٌ‫اىدائ‬ ً‫اىْظا‬ ٜ‫ف‬ ‫از‬ٞ‫اىر‬
)
.
4
-
ٜ‫طسف‬ ِٞ‫ت‬ ‫اىر٘ذس‬ ‫ػثازج‬ ُ‫أ‬ ِٞ‫ت‬
‫ؼح‬ٞ‫اى٘ش‬
‫اىشنو‬ ٚ‫ػي‬ ‫ذنرة‬
:
. ( )
ٍِ‫اىص‬ ‫ثاتد‬ ‫َح‬ٞ‫ق‬ ُ‫ا‬ٞ‫اىث‬ ٍِ ‫أٗجد‬
.
5
-
: ُ‫أ‬ ‫أثثد‬
2
2
R ( t - τ )
r =
τ

‫ث‬ٞ‫د‬
t'
‫فاصيح‬
‫ّقطح‬
‫اىََاض‬ ‫ذقاطغ‬
‫اىيذظح‬ ‫ػْد‬
.‫األشٍْح‬ ‫ٍذ٘ز‬ ‫ٍغ‬
‫أدسة‬
‫َح‬ٞ‫ق‬
ٍِ ‫مو‬
‫اىَقاٍٗح‬
ٗ
‫ح‬ٞ‫اىراذ‬
.
(:‫الثاني‬ ‫التمرين‬
17
)‫نقاط‬
‫ح‬ٝ‫مس‬
( )
‫مريرٖا‬
َٞ‫ق‬ ‫د‬ٝ‫ىرذد‬ ‫ٍجٖ٘ىح‬
‫ر‬
‫ٖا‬
‫ّقرسح‬
.
I
-
‫الطريقة‬
:‫األولى‬
‫دزاسح‬
‫اى‬ ‫دسمح‬
‫سق٘ط‬
‫اى‬
‫اىٖ٘اء‬ ٜ‫ف‬ ‫ح‬ٝ‫ىينس‬ ٜ‫شاق٘ى‬
:
‫ذسقط‬
‫اى‬
‫ح‬ٝ‫نس‬
‫ح‬ٞ‫اتردائ‬ ‫سسػح‬ ُٗ‫د‬
‫اىٖ٘اء‬ ٜ‫ف‬
‫اترداء‬
ٍِ
‫اى‬
‫ْقطح‬
‫ٍثدأ‬
‫اخ‬ٞ‫ادداث‬
ٌ‫ٍؼي‬
‫اىدزاسح‬
،
‫ق‬ٞ‫ذؼ‬
‫دسم‬
‫رٖا‬
‫ادرناك‬ ‫ق٘ج‬
ٍِ ‫ػثازذٖا‬
: ‫اىشنو‬
f Kv

.
)‫دض‬َٞ‫أزخ‬ ‫دافؼح‬ ‫َّٖو‬ (
‫اىشنو‬ ُ‫ا‬ٞ‫اىث‬ ‫َثو‬ٝ
-
8
‫ح‬ٝ‫اىنس‬ ‫ػطاىح‬ ‫ٍسمص‬ ‫سسػح‬ ‫ساخ‬ٞ‫ذغ‬
.ٍِ‫اىص‬ ‫تدالىح‬
:‫يعطى‬
2
3.57 10 /
K Kg s

 
،
2
10 /
g m s

.
1
-
‫ىدزاسح‬ ‫اىَْاسة‬ ‫اىَسجغ‬ ٕ٘ ‫ٍا‬
ٓ‫ٕر‬
‫اى‬
‫؟‬ ‫ذسمح‬
-
‫ذسَخ‬ ٜ‫اىر‬ ٗ ‫اىَسجغ‬ ‫تٖرا‬ ‫اىَرؼيقح‬ ‫ح‬ٞ‫اىفسظ‬ ٜٕ ‫ٍا‬
.‫٘ذِ؟‬ْٞ‫ى‬ ّٜ‫اىثا‬ ُّ٘‫اىقا‬ ‫ق‬ٞ‫ترطث‬
2
-
ُ‫ا‬ٞ‫اىث‬ ‫تاسرغاله‬
‫أٗجد‬
:
‫أ‬
-
‫ح‬ٝ‫اىذد‬ ‫اىسسػح‬ ‫َح‬ٞ‫ق‬
L
v
.

7. ‫الصفحة‬
7
‫من‬
8
0 0,1
1,88
𝑡( 𝑠 )
𝑣( 𝑚 𝑠 )
‫الشكل‬
–
10
‫الشكل‬
–
09
‫ب‬
-
ٍِ‫اىص‬ ‫ثاتد‬

‫ىيذسمح‬ ‫ص‬ََٞ‫اى‬
.
‫جـ‬
-
ٜ‫االتردائ‬ ‫اىرسازع‬ ‫َح‬ٞ‫ق‬
0
a
‫؟‬ ‫ذسرْرج‬ ‫ذا‬ ‫ٍا‬ ،
3
-
ٗ‫أ‬
‫ح‬ٞ‫اىرفاظي‬ ‫اىَؼادىح‬ ‫جد‬
‫ىيذسمح‬
‫اىشنو‬ ٚ‫ػي‬ ‫ذنرة‬ ‫أّٖا‬ ِٞ‫ت‬ ٗ
dv
Av B
dt
 
‫ث‬ٞ‫د‬
ٗ
‫َٖا‬ٞ‫ػثازذ‬ ‫جاد‬ٝ‫إ‬ ‫طية‬ٝ ‫ث٘اتد‬
4
-
‫ح‬ٝ‫اىنس‬ ‫مريح‬ ‫َح‬ٞ‫ق‬ ‫أدسة‬
.
II
-
‫الثانية‬ ‫الطريقة‬
:
‫دزاسح‬
‫دسمح‬
‫جَيح‬
‫ٍٖرصج‬
(
‫ّاتط‬
–
‫ح‬ٝ‫مس‬
)
ٛ‫أ‬
(
ُ‫ٍس‬ ‫ّ٘اض‬
ٜ‫أفق‬
)
:
‫ن‬
‫ثب‬
‫مرونتو‬ ‫ثابت‬ ‫متالصقة‬ ‫غير‬ ‫حمقاتو‬ ‫ن‬‫مر‬ ‫بنابض‬ ‫السابقة‬ ‫ية‬‫ر‬‫الك‬ ‫ت‬
50 /
K N m

‫موضح‬ ‫ىو‬ ‫كما‬
‫في‬
‫الشكل‬
-
9
.
‫يح‬‫ز‬‫ن‬
‫بالمقدار‬ ‫ن‬‫از‬‫و‬‫الت‬ ‫وضع‬ ‫عن‬ ‫ية‬‫ر‬‫الك‬
( )
‫و‬
‫ن‬
‫المحظة‬ ‫عند‬ ‫تركيا‬
. ‫ابتدائية‬ ‫عة‬
‫سر‬ ‫ن‬‫دو‬
‫الزمن‬ ‫بداللة‬ ‫ية‬‫ر‬‫الك‬ ‫عطالة‬ ‫مركز‬ ‫عة‬
‫سر‬ ‫تسجيل‬ ‫عمى‬ ‫بالحصول‬ ‫مناسب‬ ‫تجييز‬ ‫يسمح‬
t
‫الشكل‬ ‫البيان‬ ‫في‬ ‫الممثل‬‫و‬
(
16
)
.
1
-
‫الفاصمة‬ ‫عند‬ ‫ية‬‫ر‬‫الك‬ ‫عمى‬ ‫ة‬
‫ر‬‫المؤث‬ ‫القوى‬ ‫مثل‬
( )
.
7
-
‫حركة‬ ‫ىل‬
‫الجممة‬
‫متخامدة‬
‫ال‬ ‫أم‬
‫؟‬
‫عمل‬
.
3
-
‫لنيوتن‬ ‫الثاني‬ ‫ن‬‫القانو‬ ‫بتطبيق‬
‫أو‬
‫المعادلة‬ ‫جد‬
‫لمحركة‬ ‫التفاضمية‬
‫الفاصمة‬ ‫بداللة‬
.
4
-
‫البيان‬ ‫باستغالل‬
‫أو‬
:‫لمحركة‬ ‫ة‬
‫ز‬‫الممي‬ ‫المقادير‬ ‫جد‬

‫لمحركة‬ ‫الذاتي‬ ‫الدور‬
.

‫الحركة‬ ‫نبض‬
.

‫ات‬
‫ز‬‫ا‬
‫ز‬‫االىت‬ ‫سعة‬
.

‫االبتدائية‬ ‫الصفحة‬
𝜑
.
5
-
‫ية‬‫ر‬‫الك‬ ‫كتمة‬ ‫أحسب‬
‫سابقا‬ ‫المحسوبة‬ ‫تمك‬ ‫مع‬ ‫نيا‬‫ر‬‫قا‬ ‫ثم‬
.
‫يعطى‬
:
𝜋 1
(:‫التجريبي‬ ‫التمرين‬
17
)‫نقاط‬
‫الميثانويك‬ ‫حمض‬ ‫يعتبر‬
) ‫النمل‬ ‫حمض‬ (
‫لمنمل‬ ‫الدفاع‬ ‫وسائل‬ ‫من‬
.
‫يد‬‫ر‬‫ن‬
‫محمول‬ ‫اص‬‫و‬‫خ‬ ‫بعض‬ ‫اسة‬
‫ر‬‫د‬
‫و‬
‫ـائي‬‫م‬‫ال‬
.
I
-
‫حجما‬ ‫نضع‬
‫المولي‬ ‫التركيز‬ ‫ذي‬ ‫النمل‬ ‫حمض‬ ‫من‬
‫سعة‬ ‫ذات‬ ‫ية‬‫ر‬‫عيا‬ ‫ـة‬‫م‬‫حوج‬ ‫ـي‬‫ـ‬‫ـ‬‫ف‬
1
.‫العيار‬ ‫خط‬ ‫إلى‬ ‫المقطر‬ ‫بالماء‬ ‫الحجم‬ ‫ثم‬
‫ج‬
‫نر‬
‫جيدا‬ ‫المحمول‬
‫محمول‬ ‫عمى‬ ‫فنحصل‬
( )
‫تركيز‬ ‫ذي‬
‫المولي‬
‫عند‬
‫قياس‬
‫ناقميتو‬
‫النوعي‬
‫ة‬
‫نجد‬
.
: ‫يعطى‬
3 2
5,46 10 . /
HCOO
S m mol
 

 
،
3
3 2
35,00 10 . /
H O
S m mol
 

 

8. ‫الصفحة‬
8
‫من‬
8
1
-
‫معادلة‬ ‫أكتب‬
‫في‬ ‫الميثانويك‬ ‫حمض‬ ‫انحالل‬
. ‫الماء‬
2
-
‫أوجد‬
‫جد‬
‫بين‬ ‫العالقة‬
‫و‬
.
3
-
‫قيمة‬ ‫أحسب‬
‫المحمول‬
( )
.
4
-
‫أكتب‬
‫النيائي‬ ‫التقدم‬ ‫نسبة‬ ‫ة‬
‫ر‬‫عبا‬
f

‫المحمول‬ ‫في‬ ‫الماء‬ ‫مع‬ ‫النمل‬ ‫لحمض‬ ‫الحاصل‬ ‫لمتحول‬
( )
‫بداللة‬
.
-II
‫الميثانويك‬ ‫حمض‬ ‫بين‬ ‫يحدث‬ ‫الذي‬ ‫الكيميائي‬ ‫التفاعل‬ ‫اسة‬
‫ر‬‫د‬ ‫يد‬‫ر‬‫ن‬
‫صيغتو‬ ‫كحول‬ ‫و‬
‫المجممة‬ ‫يئية‬‫ز‬‫الج‬
. 1
‫ثما‬ ‫في‬ ‫نضع‬
‫نية‬
‫ـ‬‫ق‬‫ر‬‫م‬ ‫ـتبار‬‫خ‬‫ا‬ ‫ـيب‬‫ب‬‫أنا‬
‫من‬ ‫ـمة‬‫ـ‬
1
‫إل‬
‫ى‬
0
‫من‬ ‫ن‬‫المتكو‬ ‫يج‬‫ز‬‫الم‬ ‫نفس‬
‫ـمض‬‫ح‬‫ال‬ ‫من‬
‫و‬
‫الكحول‬ ‫من‬
‫ثم‬
‫تو‬‫ر‬‫ا‬
‫ر‬‫ح‬ ‫درجة‬ ‫مائي‬ ‫حمام‬ ‫في‬ ‫األنابيب‬ ‫ىذه‬ ‫ندخل‬
(10 )
‫ساعة‬ ‫كل‬ ‫بعد‬ ‫و‬
‫تيب‬‫ر‬‫بالت‬ ‫األنابيب‬ ‫ىذه‬ ‫أحد‬ ‫ج‬
‫نخر‬
‫من‬
1
‫إلى‬
0
‫ثم‬
، ‫الصوديوم‬ ‫ىيدروكسيد‬ ‫محمول‬ ‫اسطة‬‫و‬‫ب‬ ‫فيو‬ ‫المتبقي‬ ‫الحمض‬ ‫نعاير‬
. ( ( ) −
( ))
‫النتائج‬
‫عمييا‬ ‫المتحصل‬
: ‫التالي‬ ‫الجدول‬ ‫في‬ ‫مدونة‬
0
1
‫األنبوب‬ ‫قم‬‫ر‬
1
(ℎ )
0
0
11
(‫)حمض‬
(‫)أستر‬
1
-
. ‫أعاله‬ ‫الجدول‬ ‫أكمل‬
-
‫البياني‬ ‫المنحنى‬ ‫أرسم‬
(‫)أستر‬ ( )
.
‫وفق‬
: ‫السمم‬
( 1 1ℎ ‫و‬ 1 1 )
3
-
‫أنشئ‬
‫التفاعل‬ ‫تقدم‬ ‫جدول‬
‫الحمض‬ ‫بين‬
‫الكحول‬ ‫و‬
1
.
4
-
: ‫البيان‬ ‫من‬ ‫استنتج‬
‫أ‬
-
‫المحظة‬ ‫عند‬ ‫التفاعل‬ ‫عة‬
‫سر‬
ℎ
.
‫ب‬
-
‫حدد‬
‫ال‬
‫محظة‬
‫ىذا‬ ‫لنياية‬ ‫افقة‬‫و‬‫الم‬
‫التحول‬
‫؟‬
‫ـ‬‫ج‬
-
. ‫ة‬
‫ر‬‫األست‬ ‫مردود‬
-
‫استنتج‬
.‫الممكنة‬ ‫المفصمة‬ ‫نصف‬ ‫صيغو‬ ‫و‬ ‫المستعمل‬ ‫الكحول‬ ‫صنف‬
5
-
‫الناتج‬ ‫األستر‬ ‫تسمية‬ ‫مع‬ . ‫عة‬
‫المتفر‬ ‫الصيغة‬ ‫ذي‬ ‫الكحول‬ ‫و‬ ‫الحمض‬ ‫بين‬ ‫الحاصل‬ ‫لمتحول‬ ‫المنمذج‬ ‫التفاعل‬ ‫معادلة‬ ‫أكتب‬
6
-
‫قم‬‫ر‬ ‫األنبوب‬ ‫ج‬
‫نخر‬
‫المحظة‬ ‫عند‬
ℎ
‫ة‬
‫ر‬‫مباش‬ ‫لو‬ ‫نضيف‬ ‫ثم‬
. ‫األستر‬ ‫من‬

‫؟‬ ‫الكيميائية‬ ‫الجممة‬ ‫تطور‬ ‫تتوقع‬ ‫جية‬ ‫أي‬ ‫في‬
.‫عمل‬
‫الثاني‬ ‫ع‬
‫الموضو‬ ‫انتهى‬

9. ‫النموذجيت‬ ‫اإلجابت‬
‫المقترحت‬
‫التجريبيت‬ ‫البكالوريا‬ ‫امتحان‬ ‫لموضوع‬
-
‫دورة‬
7107
-
)‫األول‬ ‫(الموضوع‬ ‫اإلجابت‬ ‫عناصر‬
‫العالمت‬
‫مجزأة‬
‫المجموع‬
‫األول‬ ‫ين‬‫ر‬‫التم‬
(:
60
)‫نقاط‬
0
-
‫أ‬
-
‫اىحسمخ‬ ‫رسبزع‬ ‫ػجبزح‬
‫اىَسبز‬ ‫ػيى‬
AO
:
‫اىغَيخ‬ ‫ػيى‬ ِ‫ىٍْ٘ر‬ ًّ‫اىضب‬ ُّ٘‫اىقب‬ ‫ثزطجٍق‬
:‫ّغد‬ ‫غبىٍيٍب‬ ٓ‫ّؼزجس‬ ‫اىري‬ ً‫األزظ‬ ً‫اىسطح‬ ‫اىَسعغ‬ ً‫ف‬ )ٌ‫(عس‬
F .
ext m a


:ٍْٔ ٗ
.
P R m a
 
:‫ّغد‬ ‫اىغجسٌخ‬ ٌٍ‫اىق‬ ‫أخر‬ ٗ ٔ‫اىَ٘ع‬ ‫اىحسمخ‬ ‫ٍح٘ز‬ ‫ٗفق‬ ‫ثبإلسقبغ‬
. sin .
x
P m a P m a

    
:‫أي‬
m
 sin
g m
  .a
:ٍْٔ ٗ ،
sin te
a g C

  
.
‫ب‬
-
‫اىَسبز‬ ‫ػيى‬ ‫اىحسمخ‬ ‫غجٍؼخ‬
AO
‫اىز‬ ‫ٍغ‬
‫ؼي‬
ٍ
‫و‬
:
‫اىَسبز‬
ً‫ثبّزظب‬ ‫ٍزغٍسح‬ ‫ٍسزقٍَخ‬ ‫فبىحسمخ‬ ،‫صبثذ‬ ‫ٍقداز‬ ‫اىزسبزع‬ ٗ ٌٍ‫ٍسزق‬
.)‫(ٍزجبغئخ‬
7
-
‫أ‬
-
‫اىسسػخ‬ ‫شؼبع‬ ً‫ٍسمجز‬
0
v
:ٔ‫ٗغٌ٘يز‬

:)‫اىجٍبُ(أ‬ ٍِ
1
0
3 0
3 .
1 0
x x
dx
v v m s
dt


   


:)‫اىجٍبُ(ة‬ ٍِ
1
0 4 .
y
v m s 

:ٍْٔ ٗ
2 2 2 2 1
0 0 0 0 3 4 5 .
x x y
v v v v m s 
     
‫ب‬
-
‫اىصاٌٗخ‬ ‫قٍَخ‬ ‫حسبة‬

:
0
0
4
sin 0,8
5
y
y
v
v
   
:ٍْٔ ٗ
53,13
 

3
-
‫حس‬
‫ب‬
‫اىَ٘ظغ‬ ‫ػْد‬ ‫اىسسػخ‬ ‫ة‬
A
:
ٍِ‫اىَ٘ظؼ‬ ٍِ‫ث‬ )‫أزض‬+ٌ‫(عس‬ ‫اىغَيخ‬ ‫ػيى‬ ‫اىطبقخ‬ ‫اّحفبظ‬ ‫ٍجدأ‬ ‫ثزطجٍق‬
O
ٗ
A
،
‫اىْقطخ‬ ٍِ ‫اىَبز‬ ً‫األفق‬ ‫اىَسز٘ي‬ ‫ثبػزجبز‬ ٗ
A
:‫ّغد‬ ‫اىضقبىٍخ‬ ‫اىنبٍْخ‬ ‫اىطبقخ‬ ‫ىحسبة‬ ‫ٍسعغ‬
A A
A O C PP
E E E E
   O O
C pp
E E
 
1
2
A O O
C C pp
E E E m
   2 1
2
A
v m
 2
O
v m
 O
gh
‫حٍش‬
:
sin
O
h AO 

:ٍْٔ ٗ
2 2 2
2
1
2 sin 2 sin
5 (2.10.1,5.0,8)
7 .
A O A O
A
A
v v gAO v v gAO
v
v m s
 

    
 

4
-
‫أ‬
-
ٌ‫اىغس‬ ‫ػطبىخ‬ ‫ٍسمص‬ ‫ٍسبز‬ ‫ٍؼبدىخ‬
(
S
)
ٌ‫اىَؼي‬ ً‫ف‬
⃗ ⃗
:
:‫ّغد‬ ‫غبىٍيٍب‬ ٓ‫ّؼزجس‬ ‫اىري‬ ً‫األزظ‬ ً‫اىسطح‬ ‫اىَسعغ‬ ً‫ف‬ )ٌ‫(عس‬ ‫اىغَيخ‬ ‫ػيى‬ ِ‫ىٍْ٘ر‬ ًّ‫اىضب‬ ُّ٘‫اىقب‬ ‫ثزطجٍق‬
F .
ext m a


:ٍْٔ ٗ
.
P m a

:‫أي‬
a g

‫ثبإلسقبغ‬
ٌ‫اىَؼي‬ ً‫ف‬
⃗ ⃗
:
:‫ّغد‬ ‫اىغجسٌخ‬ ٌٍ‫اىق‬ ‫أخر‬ ٗ
0
x
y
a
a g



 

:‫ّغد‬ ٍِ‫اىطسف‬ ‫ثَنبٍيخ‬
0
0
.cos
. .sin
x
y
v v
v g t v





  

:‫ّغد‬ ٍِ‫اىطسف‬ ‫ثَنبٍيخ‬
0
2
0
( ) .cos . ...........(1)
1
( ) . .sin . ...........(2)
2
x t v t
y t g t v t






  


0,25
0,25
‫اىشنو‬
(
0,25
)
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
1
0,25
0,75
0,25
0,75
1,25

10. ( ٍِ
1
:‫ّغد‬ )
0 cos
x
t
v 

( ً‫ف‬ ‫ٗثبىزؼٌ٘ط‬ ،
2
:‫ّغد‬ )
 
2
2 2
0
tan
2 cos
g
y x x
v


 
  
 
 
‫ب‬
-
‫اىْقطخ‬ ‫ثؼد‬ ‫رحدٌد‬
f
‫اىْقطخ‬ ِ‫ػ‬
O
:
 
2
2 2
0
tan 0
2 cos
f f f
g
y x x
v


 
   
 
 
:ٍْٔ ٗ
 
2
2 2
0
tan
2 cos
f f
g
x x
v


 

 
 
:‫أي‬
 
2 2
0
tan
2 cos
f
g
x
v


 

 
 
:‫عددي‬ ‫تطبيق‬
2 2 2 2
0 0
2 cos (tan ) sin(2 ) 5 sin(106,26)
2 2
f
v v
x
g
  
  
2,4
f
x m

‫ث‬
-
‫اىْقطخ‬ ًٍ‫إحداص‬
H
:‫ىدٌْب‬:
sin
H
y h AO 
   
:ٍْٔ ٗ
1,2
H
y m
 
:‫ّغد‬ ‫اىَسبز‬ ‫ٍؼبدىخ‬ ً‫ف‬ ‫ثبىزؼٌ٘ط‬
2
2
1,2 0,55 1,33
0,55 1,33 1,2 0
H H
H H
x x
x x
   
  
2
(1,33) (4.0,55.( 1,2)) 4,41
    
:ٍْٔ ٗ
2,1
 
1
1,33 2,1
3,18
2.0,55
H
x m

 
:ٗ‫أ‬
2
1,33 2,1
0,58
2.0,55
H
x m

  
)‫(ٍسف٘ض‬
‫اىْقطخ‬ ‫احداصٍبد‬ ٍْٔ ٗ
H
:ًٕ
(3,18; 1,2)
H 
.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,75
1
‫الثاني‬ ‫ين‬‫ر‬‫التم‬
(:
60
)‫نقاط‬
1
–
‫أ‬
-
‫إشؼبع‬
: ُ‫أل‬
‫ب‬
-
‫اإلّحفبظ‬ ًّّ٘‫قب‬ ٍِ
:
{
: ‫اىشنو‬ ٍِ ‫اىَؼبدىخ‬ ٍْٔٗ
‫د‬
-
:ً‫اإلشؼبػ‬ ‫اىزْبقص‬ ُّ٘‫قب‬
)
(1)
.........
) ̀ )
̀
2
-
‫أ‬
-
:ُ‫اىجٍب‬ ٍِ
‫ة‬
-
: ‫اىشنو‬ ٍِ ٔ‫ٍؼبدىز‬ ُ‫اىجٍب‬
̀
‫حٍش‬
:
( : ‫اىشنو‬ ٍِ ‫اىَؼبدىخ‬ ُ‫اذ‬
2
......)
̀
‫ث‬
( ‫اىَؼبدىخ‬ ‫َطبثخ‬
1
( ‫اىَؼبدىخ‬ ‫)ٍغ‬
2
: ‫ّغد‬ )
‫ت‬
-
3
-
‫أ‬
-
̀
‫ب‬
-
̀
0,25
0,25
0,5
0,5
1,25
0,5
1,25
0,5
1
1

11. ) ) ) )
) ) ) )
‫يبي‬‫ر‬‫التج‬ ‫ين‬‫ر‬‫التم‬
(:
60
)‫نقاط‬
I
-
ًٌ٘ٗ‫اىَغٍْص‬ ُ‫ٍٗؼد‬ ‫اىحَط‬ ٍِ‫ث‬ ‫اىحبدس‬ ً‫اىنٍٍَبئ‬ ‫ىيزح٘ه‬ ‫اىصٍٍْخ‬ ‫اىَزبثؼخ‬
:
0
-
‫أ‬
-
ُ‫رجٍب‬
‫حَط‬ ( ‫ىيغَيخ‬ ‫اىحبدس‬ ‫اىزح٘ه‬ ُ‫أ‬
-
ٍ
‫أمسدح‬ ‫رفبػو‬ ُ‫أ‬ ‫ػجبزح‬ )ُ‫ؼد‬
-
‫إزعبع‬
:
: ‫اإلزعبع‬ ‫رفبػو‬
) ) )
:‫األمسدح‬ ‫رفبػو‬
) )
: ‫األٌٍّ٘خ‬ ‫اإلعَبىٍخ‬ ‫اىَؼبدىخ‬
) ) ) ) )
7
-
1
-
ً‫اىَ٘ى‬ ‫اىزسمٍص‬ ‫اسزْزبط‬
: ‫اىَسزؼَو‬ ‫اىَبء‬ ‫مي٘ز‬ ‫حَط‬ ‫ىَحي٘ه‬
‫ق٘ي‬ ‫حَط‬ ‫اىَبء‬ ‫مي٘ز‬ ‫حَط‬ ُ‫إ‬
:
[ ]
‫حٍش‬ ،
ٍٔ‫ٗػي‬
7
-
7
-
: ًَ‫األػظ‬ ً‫اىزقد‬ ‫حسبة‬ ٌ‫ص‬ ‫اىَحد‬ ‫اىَزفبػو‬ ٍٍِ‫رؼ‬
ً‫ٗاىزقد‬ ًٌ٘‫اىَغٍْص‬ ُ‫ٍؼد‬ ٕ٘ ‫اىَحد‬ ‫اىَزفبػو‬ ٍٔ‫ػي‬ ٗ
ًَ‫األػظ‬
7
-
3
-
ً‫اىزقد‬ ‫ػجبزح‬
)
‫اىيحظخ‬ ً‫ف‬ ‫ىيزفبػو‬
: ‫ثدالىخ‬
ٗ
:
:ً‫اىزقد‬ ‫ثغدٗه‬ ‫ثبالسزؼبّخ‬
) ) ) ) )
‫ث٘فسح‬
: ُ‫فئ‬
)
)
: ‫حٍش‬
)
ٗ
: ٍٔ‫ػي‬ ٗ
) )
)*(
7
-
4
-
: ً‫رب‬ ‫اىزح٘ه‬ ‫ٕرا‬ ‫فؼال‬ ُ‫أ‬ ٍِ ‫اىزأـند‬
‫ىَب‬
: ُ‫فئ‬
: ‫ّغد‬ ، )*( ‫اىؼالقخ‬ ٍِ ٗ
ً‫رب‬ ‫اىزح٘ه‬ ‫ٕرا‬ ‫فؼال‬ ٍٔ‫ػي‬ ٗ
7
-
5
-
‫اىزفبػو‬ ‫ّصف‬ ٍِ‫ش‬ ‫رحدٌد‬
⁄
:
: ‫اىزفبػو‬ ٍِ‫ش‬ ‫رؼسٌف‬ ٍِ ‫ىدٌْب‬
⁄ ⁄
: ‫ّغد‬ )*( ‫اىؼالقخ‬ ٍِ
⁄ ⁄
[ ] ⁄
:ٍْٔٗ
⁄
: ٍٔ‫ٗػي‬
⁄
7
-
6
-
‫ىيزفبػو‬ ‫اىحغٍَخ‬ ‫اىَز٘سطخ‬ ‫اىسسػخ‬ ‫حسبة‬
ٍِ‫اىيحظز‬ ٍِ‫ث‬
ٗ
: ‫ىيزفبػو‬ ‫اىَز٘سطخ‬ ‫اىسسػخ‬ ‫رؼسٌف‬ ٍِ
( )
: ‫حٍش‬
)
‫ٍغ‬
)
:ٍٔ‫ٗػي‬
)
II
:
‫ىألٍٍّ٘بك‬ ‫اىزغبزي‬ ‫اىَحي٘ه‬ ‫ٍؼبٌسح‬
:
1
-
:‫اىَؼبٌسح‬ ‫ىزفبػو‬ ‫اىنٍٍَبئٍخ‬ ‫اىَؼبدىخ‬ ‫مزبثخ‬
2
-
‫أ‬
-
: ‫اىزنبفؤ‬ ‫ّقطخ‬ ‫رؼسٌف‬
‫سزنٍٍ٘زسٌخ‬ ‫ثْست‬ ُ‫اىَزفبػال‬ ‫فٍٖب‬ ُ٘‫ٌن‬ ً‫اىز‬ ‫اىْقطخ‬ ‫ريل‬ ًٕ
.
-
:‫إحداصٍزٍٖب‬ ‫اسزْزبط‬
)
‫ب‬
-
ً‫اىَ٘ى‬ ‫اىزسمٍص‬ ‫حسبة‬
‫ىيَحي٘ه‬
:
: ‫اىزنبفؤ‬ ‫ػْد‬
: ٍٔ‫ػي‬ ٗ
*
-
ً‫اىَ٘ى‬ ‫اىزسمٍص‬ ‫اسزْزبط‬
‫ىيَحي٘ه‬
:
‫ج‬
-
: ‫اىْبرظ‬ ‫اىَحي٘ه‬ ‫غجٍؼخ‬
)ًٍٍّ٘٘‫األ‬ ‫مي٘ز‬ ‫ٍحي٘ه‬ ( ً‫حبٍع‬ ً‫ٍيح‬ ‫فبىَحي٘ه‬ ٍٔ‫ػي‬ ٗ
-
: ‫اىزفسٍس‬
‫ش٘ازد‬ ‫ر٘اعد‬
)
. ً‫حبٍع‬ ‫اى٘سػ‬ ُ‫أ‬ ‫ػيى‬ ‫دالىخ‬
3
-
‫أ‬
-
‫قٍَخ‬ ُ‫اىجٍب‬ ٍِ ‫إٌغبد‬
‫أعو‬ ٍِ
:
‫ب‬
-
: ً‫رب‬ ‫اىَؼبٌسح‬ ‫رفبػو‬ ُ‫ا‬ ُ‫رجٍب‬
‫ط‬
-
0
-
:
‫اىَدزٗسخ‬ ‫ىيغَيخ‬ ُ‫اىز٘اش‬ ‫صبثذ‬ ‫حسبة‬
:
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,25
0,25
0,25
0,25
0,25
0,75
0,5
0,5
0,5
0,25
0,5
0,5
0,25
0,75
0,5
0,5
0,25

12. [ ]
[ ] [ ]
) ) ) )
: ‫ىدٌْب‬
: ّٔ‫فئ‬
: ٍْٔٗ
. ً‫رب‬ ‫رفبػو‬ ‫اىَؼبٌسح‬ ‫رفبػو‬ ٍٔ‫ٗػي‬
‫ط‬
-
7
-
:
: ً‫اىْٖبئ‬ ً‫اىزقد‬ ‫ّسجخ‬ ‫حسبة‬
: ‫ىدٌْب‬
: ً‫اىزقد‬ ‫ثغدٗه‬ ‫ثبالسزؼبّخ‬
‫ث٘فسح‬
*
-
:
ٍٔ‫ػي‬ ٗ ‫اىَبء‬ ‫مي٘ز‬ ‫حَط‬ ٕ٘ ‫اىَحد‬ ‫اىَزفبػو‬ ٍْٔ ٗ
*
-
:
)
: ٍْٔ ٗ
)
: ‫أخٍسا‬ ٗ
)
ً‫رب‬ ‫اىزح٘ه‬ ‫فٖرا‬ ٍٔ‫ٗػي‬
4
-
‫حبىخ‬ ً‫ف‬ ُ٘‫ٍي‬ ‫مبشف‬ ِ‫أحس‬ ‫اخزٍبز‬ ً‫ف‬ ٓ‫ّؼزَد‬ ‫اىري‬ ‫اىَؼٍبز‬
: ‫اىيٍّ٘خ‬ ‫اىَؼبٌسح‬ ‫إعساء‬
-
‫قٍَخ‬
. ‫ىينبشف‬ ًّ٘‫اىي‬ ‫اىزغٍس‬ ‫ٍغبه‬ ‫إىى‬ ًَ‫رْز‬
-
. ‫أصغسي‬ ‫ىينبشف‬ ًّ٘‫اىي‬ ‫اىزغٍس‬ ‫ٍغبه‬
0,25
0,25
0,25
0,25
0,25
0,75
0,5

13. ‫الثاني‬ ‫للموضوع‬ ‫النموذجي‬ ‫التصحيح‬
‫احلل‬ ‫عناصر‬
‫التنقيط‬
‫ين‬‫ر‬‫التم‬
10
:
10
/
10
I
–
‫األومي‬ ‫الناقل‬ ‫مقاومة‬ ‫قيمة‬ ‫ايجاد‬
R
:
1
-
1
-
‫ط‬
1
.‫الدارة‬ ‫يف‬ ‫التسلسل‬ ‫على‬ ‫مرت‬ ‫أمبري‬ ‫و‬ ‫املكثفة‬ ‫مع‬ ‫ع‬
‫التفر‬ ‫على‬ ‫مرت‬ ‫لط‬‫و‬‫ف‬ ‫بط‬‫ر‬‫ن‬ :
‫ط‬
2
:
‫باستعمال‬
‫اسم‬‫ر‬
‫از‬‫ز‬‫االهت‬
‫املدخل‬ : ‫حيث‬ ‫ذاكرة‬ ‫ذو‬ ‫املهبطي‬
Y1
‫املدخل‬ ‫و‬ ‫املكثفة‬ ‫طريف‬ ‫بني‬
Y2
‫األومي‬ ‫الناقل‬ ‫طريف‬ ‫بني‬
.
‫ط‬
3
‫بإستعمال‬ :
EXAO
. ‫الدارة‬ ‫مع‬ ‫التسلسل‬ ‫على‬ ‫التيار‬ ‫القط‬ ‫بط‬‫ر‬‫ن‬ ‫و‬ ‫املكثفة‬ ‫طريف‬ ‫بني‬ ‫التوتر‬ ‫القط‬ ‫بط‬‫ر‬‫ن‬ ‫حيث‬
1
-
2
-
: ‫ات‬‫ر‬‫التوت‬ ‫مجع‬ ‫قانون‬ ‫من‬
( ) ( )
( ) ( )
( )
( )
( ) 1
( )
c R
c
c
c
c
c
u t u t E
u t Ri t E
du t
u t RC E
dt
du t E
u t
dt RC RC
 
 
 
 
-1
3
-
:‫لدينا‬
( )
( )
{
t
c
t
c
u t A Be
du t
Be
dt



 

:‫جند‬ ‫التفاضلية‬ ‫املعادلة‬ ‫يف‬ ‫بالتعويض‬
1
( )
1
0
t t
t
E
Be A Be
RC RC
A E
Be
RC RC RC
 



  
 
   
 
 
: ‫ومنه‬
1
1 1 1
0
0
RC RC
A E
A E
RC RC
 

      
   
B
:‫حيث‬ ‫اإلبتدائية‬ ‫الشروط‬ ‫من‬ ‫نستنتجه‬
(0) 0 0
c
u A B B A E
        
4
-
1
/
( ) (1 )
t
c
u t E e 

 
: ‫ومنه‬
1 1
/ /
( ) ( ) (1 )
t t
R c
u t E u t E E e Ee
 
 
     
5
-
/‫أ‬
1
1 1 1
1
/
/ / /
/
( ) (1 )
(1 ) 1
( )
t
t t t
c
t
R
u t E e
e e e
u t Ee

  





    
: ‫السابقة‬ ‫العبارة‬ ‫من‬ /‫ب‬
1 1
/
1
1
( )
1 1 1.71
( )
c
R
u
e e
u
 


    
: ‫جند‬ ‫البيان‬ ‫على‬ ‫باإلسقاط‬
1 20ms
 
: ‫لدينا‬
3
1 6
20.10
20 40
500.10
RC ms R



     
6
-
2 6 2 3
1 1
.500.10 .6 9.10
2 2
c
E CE joule
 
  
II
–
‫المقاومة‬ ‫من‬ ‫كل‬‫قيمة‬ ‫ايجاد‬
r
‫الذاتية‬ ‫و‬
L
:
1
-
.‫ذاكرة‬ ‫ذو‬ ‫املهبطي‬ ‫از‬‫ز‬‫االهت‬ ‫اسم‬‫ر‬ ‫هو‬ ‫اجلهاز‬
: ‫التوصيل‬ ‫يقة‬‫ر‬‫ط‬
0.25
0.25
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0

14. ‫احلل‬ ‫عناصر‬
‫التنقيط‬
2
-
: ‫التفاضلية‬ ‫املعدلة‬
: ‫ات‬‫ر‬‫التوت‬ ‫مجع‬ ‫قانون‬ ‫من‬
 
( ) ( )
( ) ( )
( )
b R
u t u t E
di
ri t L Ri t E
dt
r R
di E
i t
dt L L
 
  

 
3
-
2
/
0
( ) (1 )
t
i t I e 

 
: ‫جند‬ ‫التفاضلية‬ ‫املعادلة‬ ‫يف‬ ‫التعويض‬ ‫و‬ ‫باالشتقاق‬ : ‫التفاضلية‬ ‫للمعادلة‬ ‫حل‬
 
   
2 2
2 2
/ /
0
0
2
/ /
0
0 0
2
(1 )
t t
t t
R r
I E
e I e
L L
R r R r
I E
e I I e
L L L
E E
L L
 
 


 
 

  
 
  

4
-
: ‫لدينا‬
/ 2
0 0
( ) ( )
( ) t
di
ub t ri t L
dt
ub t rI RI e 

 
 
5
-
2 20ms
 
6
-
‫املماس‬ ‫معادلة‬
( )
ub t at b
 
‫حيث‬
0
0 2
0
( )
( 0) ( )
b
t
du t RI
a
dt
b ub t R r I E


  
  
  
 

     

: ‫ومنه‬
0
2
( )
RI
ub t t E

  
‫ملا‬
t=t'
‫يكون‬
ub(t')=0
0
0
2
( ') ' ( ) 0
b
RI
u t t R r I

    
0
0 2
2
' ( ) ' ( )
RI
t R r I Rt R r


    
2
2
( ' )
R t
r



 
7
–
:‫البيان‬ ‫من‬
3
' 24.10
t s


: ‫ومنه‬
40(24 20)
8
20
r

  
.
3
2 20 48.20.10 0,96
( )
L
ms L H
R r
 
    

‫الثاني‬ ‫ين‬‫ر‬‫التم‬
:
10
/
10
‫ا‬
: ‫الهواء‬ ‫في‬ ‫صلب‬ ‫لجسم‬ ‫لي‬‫و‬‫الشاق‬ ‫السقوط‬ ‫كة‬
‫حر‬ ‫اسة‬‫ر‬‫د‬ : ‫األولى‬ ‫لمجموعة‬
1
-
‫أرضي‬ ‫سطحي‬ : ‫ية‬‫ر‬‫الك‬ ‫كة‬
‫حر‬ ‫لدرسة‬ ‫املناسب‬ ‫املرجع‬
. ‫منتظمة‬ ‫مستقيمة‬ ‫كة‬
‫حر‬ ‫يتحرك‬ ‫أو‬ ‫ساكن‬ ‫غاليلي‬ ‫معلم‬: ‫الفرضية‬
2
-
‫أ‬
-
‫قيمة‬
14 /
L
v m s

،
‫ب‬
-
‫الزمن‬ ‫ثابت‬
1.4s
 
:
‫االبتدائي‬ ‫ع‬
‫التسار‬
  2
0
0
14 0
tan 10 /
1.4 0
t
dv
a m s
dt



   
   
   

   
.
: ‫أن‬ ‫نستنتج‬
2
0 10 /
a g m s
 
0.25
52.0
0.25
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
52.0
0.25
0.25
0.25
0.25
0.25
0.25

15. ‫احلل‬ ‫عناصر‬
‫التنقيط‬
3
-
: ‫لنيوتن‬ ‫الثاين‬ ‫القانون‬ ‫حسب‬ : ‫التفاضلية‬ ‫املعادلة‬
G
Fext ma


G
P f ma
 
‫احملور‬ ‫على‬ ‫باإلسقاط‬
( ' )
x x
: ‫جند‬
dv dv K
Kv mg ma m v g
dt dt m
       
: ‫حيث‬
K
A
m
B g

 


 

5
-
‫الكتلة‬ ‫قيمة‬ ‫إجياد‬
m
:
m
K
 
: ‫جند‬ ‫بالتعويض‬
2
. 1.4 3.57 10 0.05 50
m K kg g
 
     
II
–
‫نابض‬ ( ‫مهتزة‬ ‫مجلة‬ ‫كة‬
‫حر‬ ‫اسة‬‫ر‬‫د‬ : ‫الثانية‬ ‫اجملموعة‬
–
)‫ية‬‫ر‬‫ك‬
.
1
-
( ‫الفاصلة‬ ‫عند‬ ‫ية‬‫ر‬‫الك‬ ‫على‬ ‫املؤثرة‬ ‫القوة‬ ‫متثل‬
x
.)
2
-
.‫الزمن‬ ‫مرور‬ ‫مع‬ ‫ثابتة‬ ‫از‬‫ز‬‫اهل‬ ‫سعة‬ :‫ير‬‫رب‬‫الت‬ ، ‫متخامدة‬ ‫غري‬ ‫از‬‫ز‬‫اهل‬ ‫كة‬
‫حر‬
3
-
: ‫از‬‫ز‬‫اهل‬ ‫كة‬
‫حلر‬ ‫التفاضلية‬ ‫املعادلة‬
: ‫لنيوتن‬ ‫الثاين‬ ‫القانون‬ ‫حسب‬
G
Fext ma


G
P R F ma
  
‫باالسقاط‬
‫املوجه‬ ‫احملور‬ ‫على‬
(x'x)
: ‫جند‬
2 2
2 2
0 0 0
d x d x K
Kx m x
dt dt m
     
3
-
‫كة‬
‫للحر‬ ‫الذايت‬ ‫الدور‬
0 0.2
T s

،
: ‫كة‬
‫احلر‬ ‫نبض‬
0
0
2 2
10 31.4 /
0.2
rad s
T
 
 
   
،
: ‫االبتدائية‬ ‫الشروط‬ ‫من‬: ‫االبتدائية‬ ‫الصفحة‬
‫املطال‬ ‫معادلة‬ ‫من‬
x(t)
‫أجل‬ ‫من‬
t=0
: ‫جند‬
0 0
cos( ) 1 0
 
  
‫السرعة‬ ‫معادلة‬ ‫من‬ ‫أو‬
v(t)
‫أجل‬ ‫من‬
t=0
: ‫جند‬
sin( ) 0 0
 
  
4
-
‫الكتلة‬ ‫قيمة‬ ‫اجياد‬
m
:
3
0 2 2 2
0
50 50
50.10 50
10 1000
k K
m Kg g
m

 

      
‫يبا‬‫ر‬‫تق‬ ‫سايقا‬ ‫احملسوبة‬ ‫القيمة‬ ‫نفس‬ ‫هي‬ ‫و‬
‫القياس‬ ‫أخطاء‬ ‫حدود‬ ‫يف‬
.
‫التجريبي‬ ‫ين‬‫ر‬‫التم‬
10
/
10
1
–
1
: ‫التفاعل‬ ‫معادلة‬ )




 O
H
HCOO
O
H
HCOOH 3
2
1
–
2
‫بني‬ ‫العالقة‬ )
0
C
‫و‬
A
C
:
: ‫التمديد‬ ‫قانون‬ ‫من‬ ‫لدينا‬
0 0
0 0
0
100
. . 50 50
2
A
A A
C C
V
C V C V
C V C
      
1
–
3
‫قيمة‬ ‫)حساب‬
pH
‫احمللول‬
A
S
: ‫لدينا‬:
   
1
log 3 

 
f
O
H
pH
: ‫لدينا‬ ‫و‬
     
2
3
3


 


 f
HCOO
f
O
H
HCOO
O
H 


3 f f
H O HCOO
 
   

   
‫العالقة‬ ‫يف‬ ‫بالتعويض‬ ‫و‬
 
2
:
   

 
 
HCOO
O
H
f
O
H 

 3
3
: ‫منه‬ ‫و‬
   
3
3 3
3 3
0.25
6.18 / 6.18 10 /
35 5.46 10
f
H O HCOO
H O mol m x mol L

 
 
 

     
   

0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.5
0.25
0.25
.
0.25
0.25
R
P
F
X'
x
P
f

16. ‫العالقة‬ ‫من‬ ‫و‬
 
1
: ‫جند‬
  2
.
2
10
18
.
6
log 3


 
x
pH
‫احلل‬ ‫عناصر‬
‫التنقيط‬
1
–
4
: ‫النهائي‬ ‫التقدم‬ ‫نسبة‬ )
: ‫لدينا‬
3 3
max .
f f f
f
A A
H O V H O
x
x C V C

 
   

   
  
: ‫أن‬ ‫حيث‬ ‫و‬
50
0
C
CA 
: ‫فإن‬ ،
3
0
50
f
f
H O
C


  
 

2
-
1
)
: ‫اجلدول‬ ‫إمتام‬
)
‫متبقي‬ ‫محض‬
(
- n
=0 ,200
‫متشكل‬ ‫أسرت‬ (
n(
‫متفاعل‬ ‫محض‬ ( =
n(
2
-
)
‫المنحنى‬ ‫رسم‬
= f (t)
)‫(أستر‬
n
.
3
-
‫التقدم‬ ‫جدول‬
: ‫التقدم‬ ‫حدول‬ ‫إنشاء‬ )
4
‫)استنتاج‬
‫التفاعل‬ ‫سرعة‬ )‫أ‬ : ‫البٌان‬ ‫من‬
V(t=2h)
: ‫التقدم‬ ‫جدول‬ ‫من‬
)
(ester
n
x 
:
dt
ester
dn
dt
dx
v
)
(


‫حٌث‬
dt
dx
. ‫المعتبرة‬ ‫اللحظة‬ ‫عند‬ ‫للمنحنى‬ ‫المماس‬ ‫مٌل‬ ‫ٌمثل‬
2
2 1
(11,6 8.2).10
1.7 10 .
(4 0).0,5
v mol h

 

  

08
07
06
05
04
03
02
01
‫األنبوب‬ ‫رقم‬
7
6
5
4
3
2
1
0
t (heure)
0,067
0,067
0,067
0,068
0,074
0,084
0,114
0,200
n )‫((حمض‬mol)
0,133
0,133
0,133
0,132
0,126
0,116
0,086
0
)‫(أستر‬n
2
HCOOH R OH HCOO R H O
    
‫التفاعل‬ ‫معادلة‬
1
1
2 .10-1
2 .10-1
‫الحالةاالبتدائية‬
x
x
2 .10-1
-x
2 .10-1
-x
‫الحالةاالنتقالية‬
xf
xf
2. 10-1
- xf
2. 10-2
-xf
‫الحالةالنهائية‬
0.25
0.25
0.25
0.25
0.5
0.5
0.25
0.25
10-2
mol
0,5h
t
)
(ester
n

17. ‫احلل‬ ‫عناصر‬
‫التنقيط‬
: ً‫ه‬ ‫انتهى‬ ‫قد‬ ‫التحول‬ ‫أن‬ ‫فٌها‬ ‫نعتبر‬ ‫أن‬ ‫ٌمكن‬ ً‫الت‬ ‫اللحظة‬ )‫ب‬
t = 5h
: ‫األسترة‬ ‫مردود‬ )‫جـ‬
‫لدٌنا‬
67
,
0
665
,
0
2
,
0
133
,
0
max




x
xf
f

‫منه‬ ‫و‬
% .100 67%
f
R 
 
. ً‫أولــ‬ ‫المستعمل‬ ‫الكحول‬ ، ‫األسترة‬ ‫مردود‬ ‫قٌمة‬ ‫حسب‬ : ‫الكحول‬ ‫صنف‬ )‫د‬
: ً‫ه‬ ‫المستعمل‬ ً‫األول‬ ‫للكحول‬ ‫المفصلة‬ ‫نصف‬ ‫الصٌغ‬
OH
CH
CH
CH
CH 


 2
2
2
3
،
OH
CH
CH
CH 

 2
3
3
CH
5
: ‫التفاعل‬ ‫معادلة‬ ‫كتابة‬ )
O
+ H2O
3
2 CH
CH
CH 

H -C-O-
=
OH
CH
CH
CH 

 2
3
+
HCOOH
3
CH
3
CH
‫مٌثانوات‬
2
-
‫بروبٌل‬ ‫مٌثٌل‬
6
:‫الجملة‬ ‫تطور‬ ‫جهة‬ ‫توقع‬ )
: ‫التوازن‬ ‫ثابت‬ ‫إذن‬ ً‫أول‬ ‫الكحول‬ ‫و‬ ‫الموالت‬ ‫متساوي‬ ً‫االبتدائ‬ ‫المزٌج‬ ‫لدٌنا‬ ‫ــ‬
2
2
0,133
4
0,067
f
K Qr
  
‫ٌكون‬ ‫اإلضافة‬ ‫عند‬
:
: ً‫االبتدائ‬ ‫التفاعل‬ ‫كسر‬ ‫لحسب‬
87
,
9
067
,
0
133
,
0
).
2
,
0
133
,
0
(
2



i
Qr
‫أن‬ ‫نالحظ‬
K
Qri 
‫إمــــاهة‬ ‫باتجاه‬ ‫تتطور‬ ‫الجملة‬ ‫أن‬ ‫نستنتج‬ ‫منه‬ ‫و‬
‫األستر‬
.
‫األستر‬ + ‫الماء‬
=
‫الحمض‬ + ‫الكحول‬
‫التفاعل‬ ‫معادلة‬
0.133mol
(0,133 + 0,2 )mol
0,067 mol
0,067 mol
‫الحالةاال‬
‫بتدائٌة‬
0.25
0.25
0.25
0.25
0.25
0.5
0.25
0.25
0.25
0.25
0.25