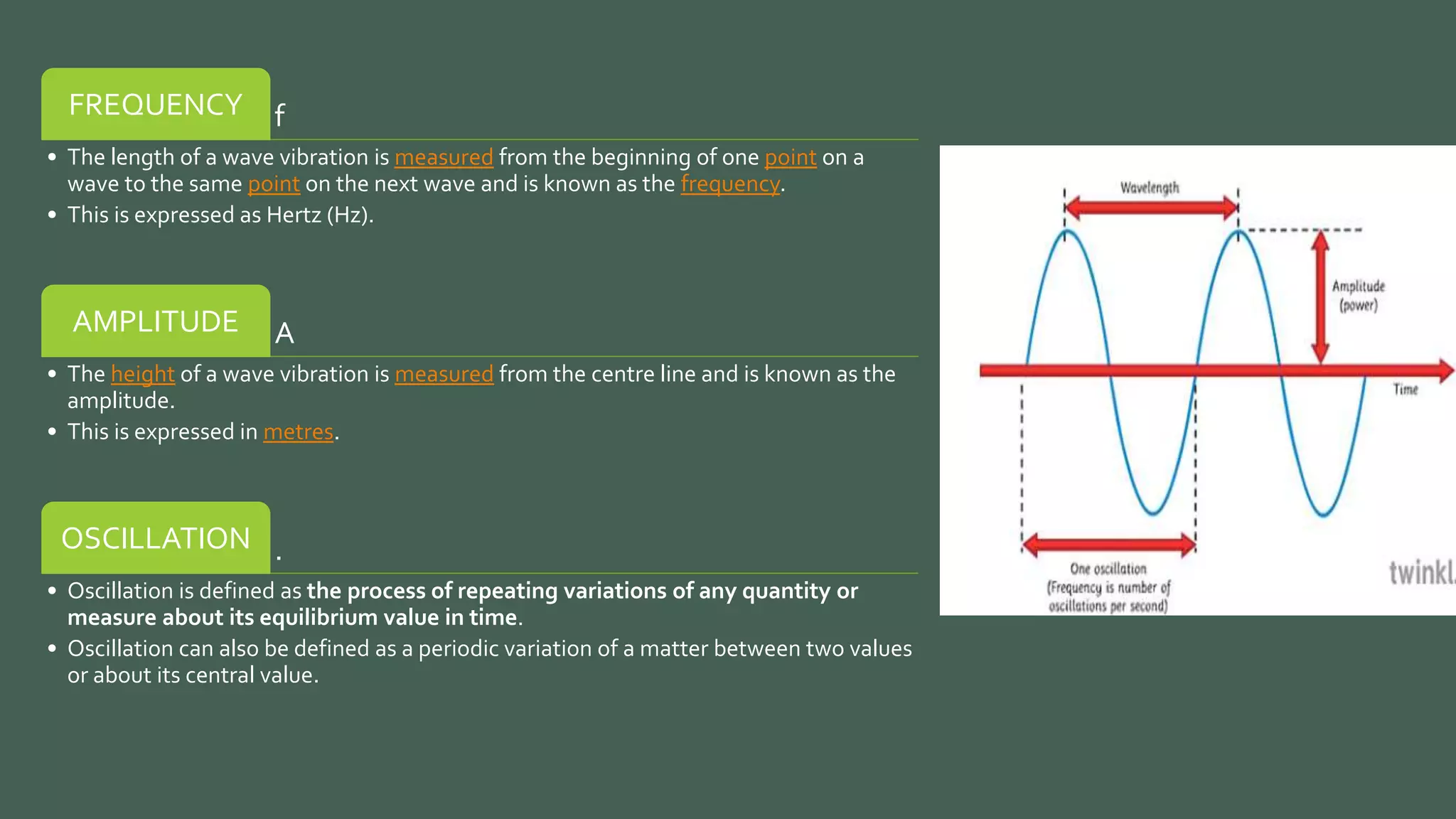
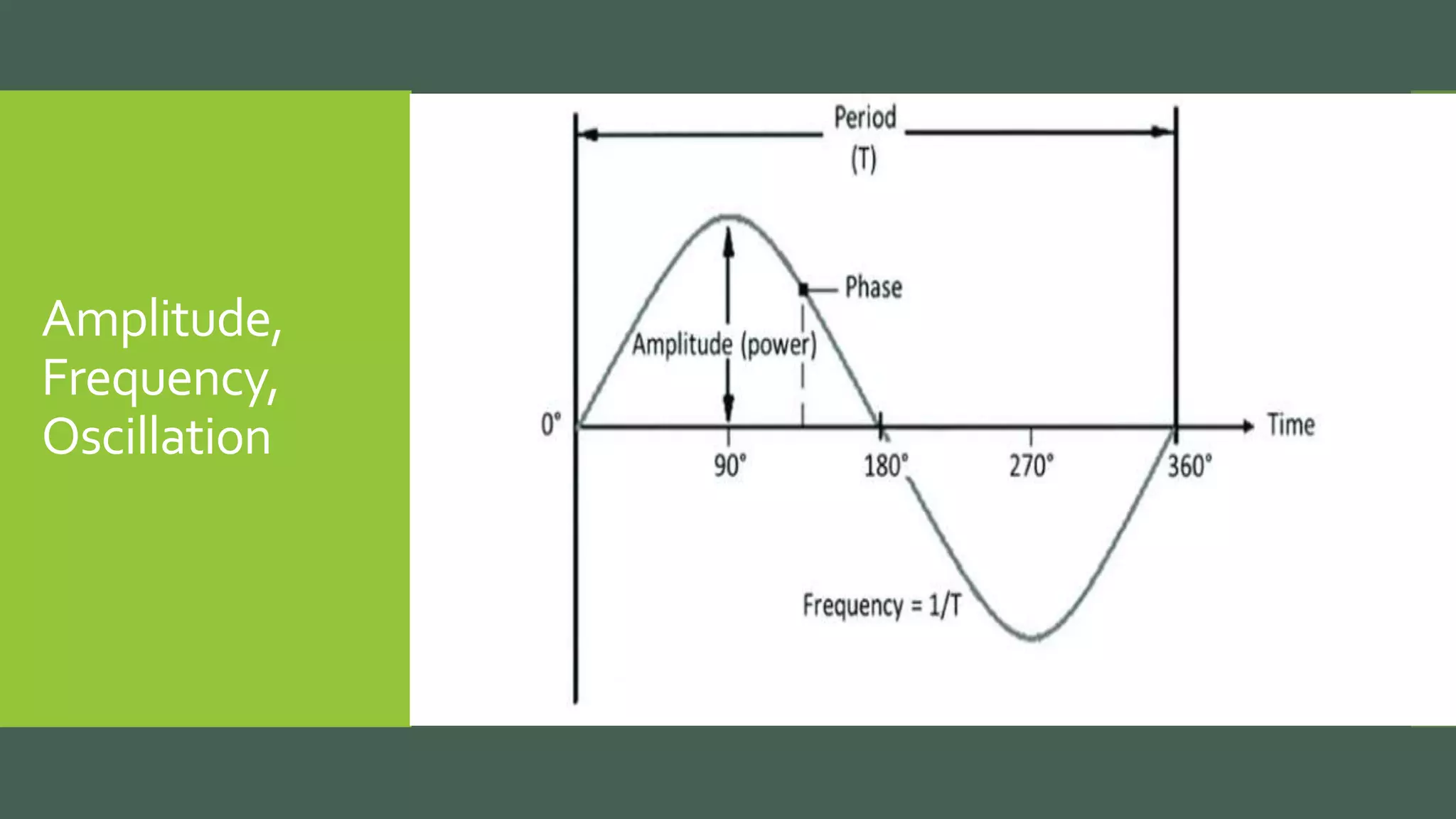
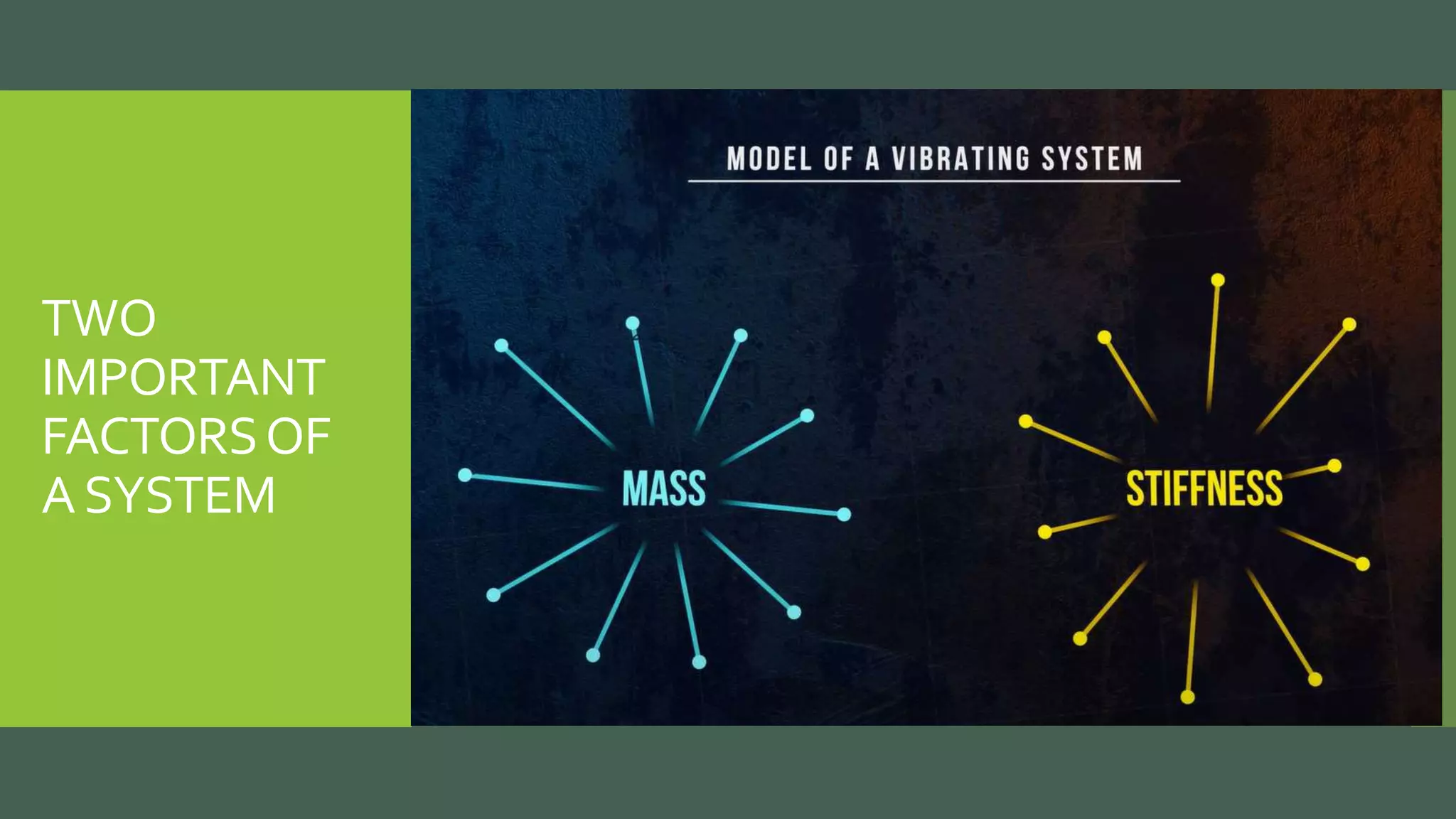
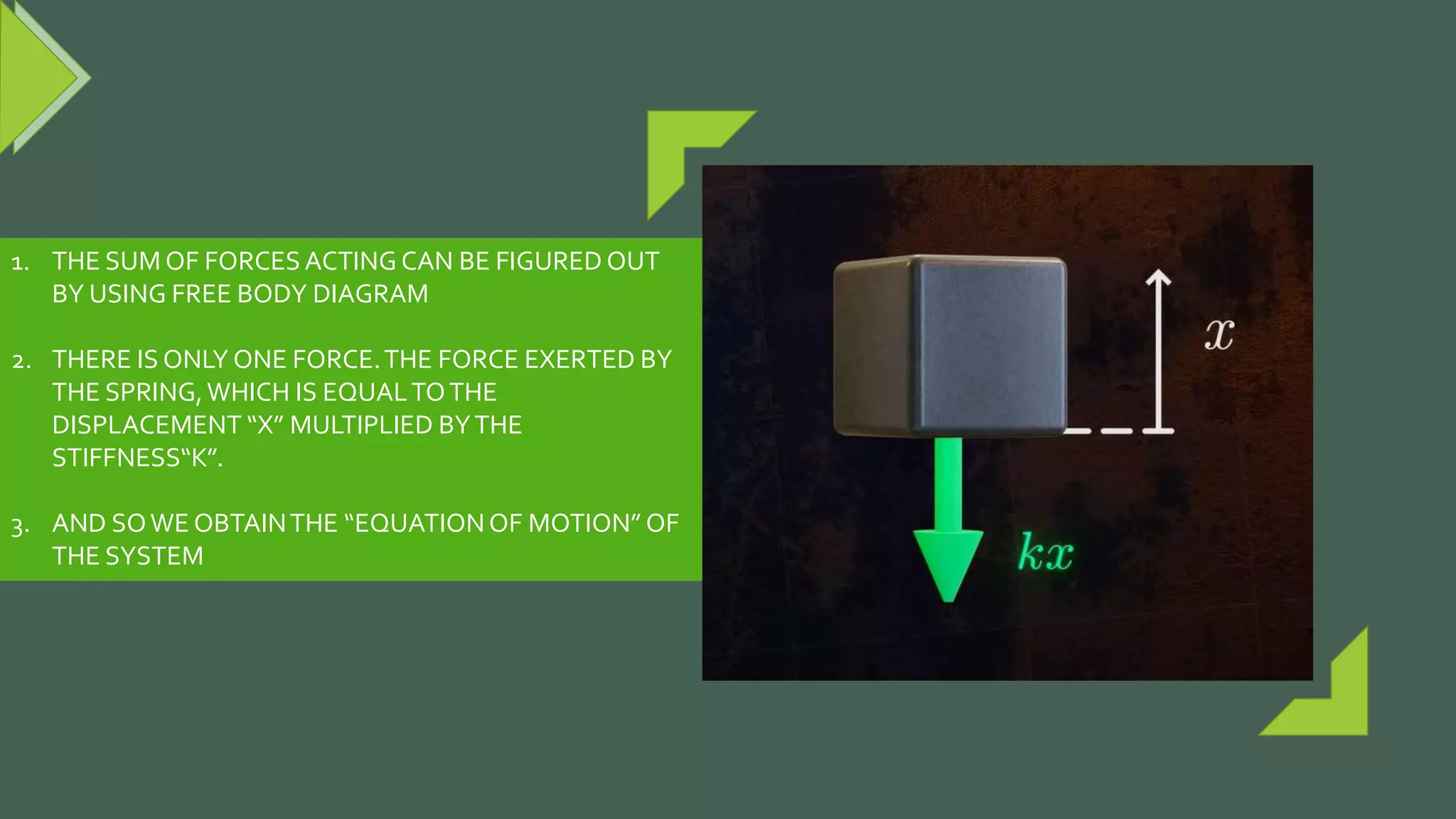
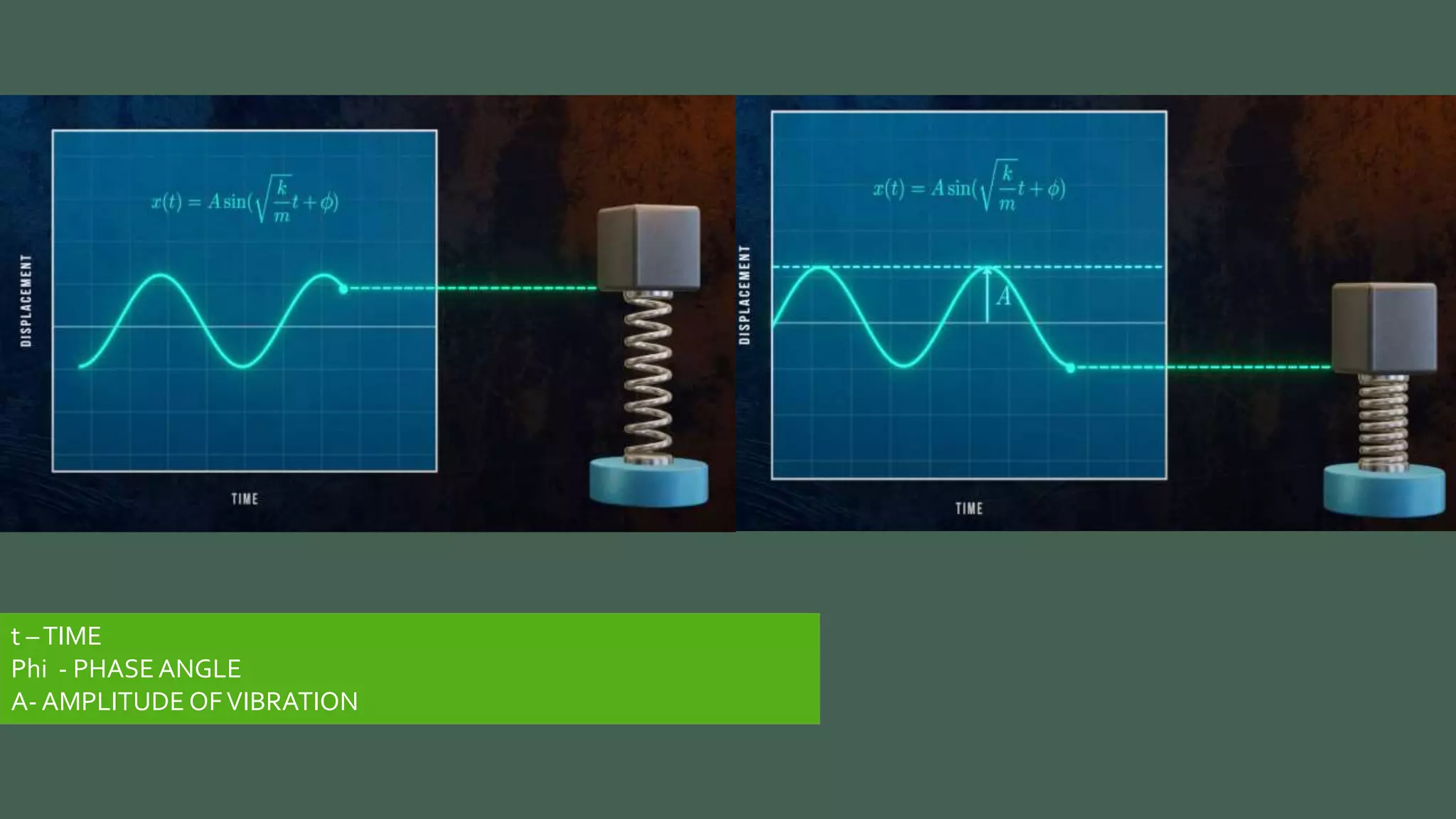
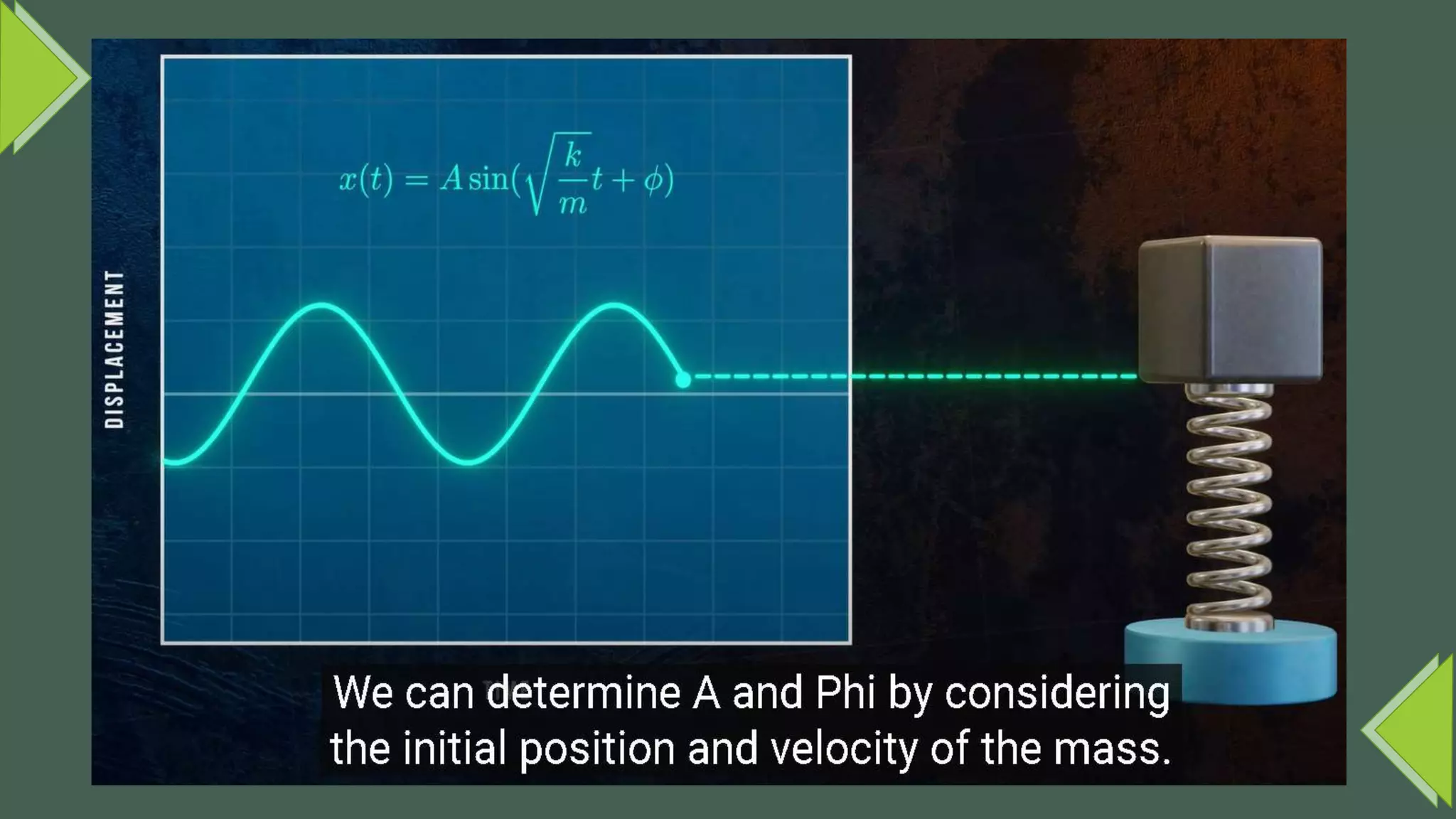
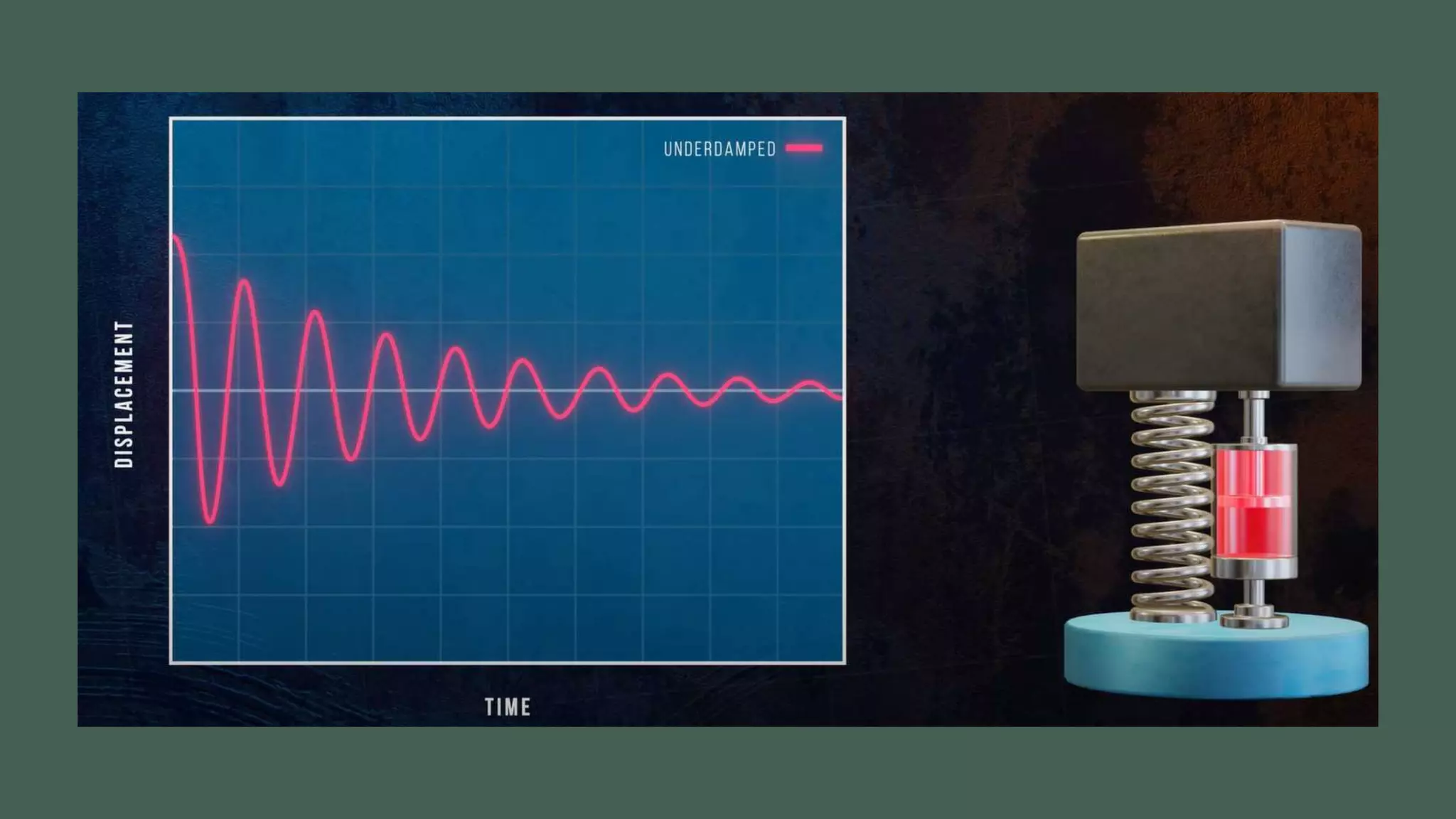
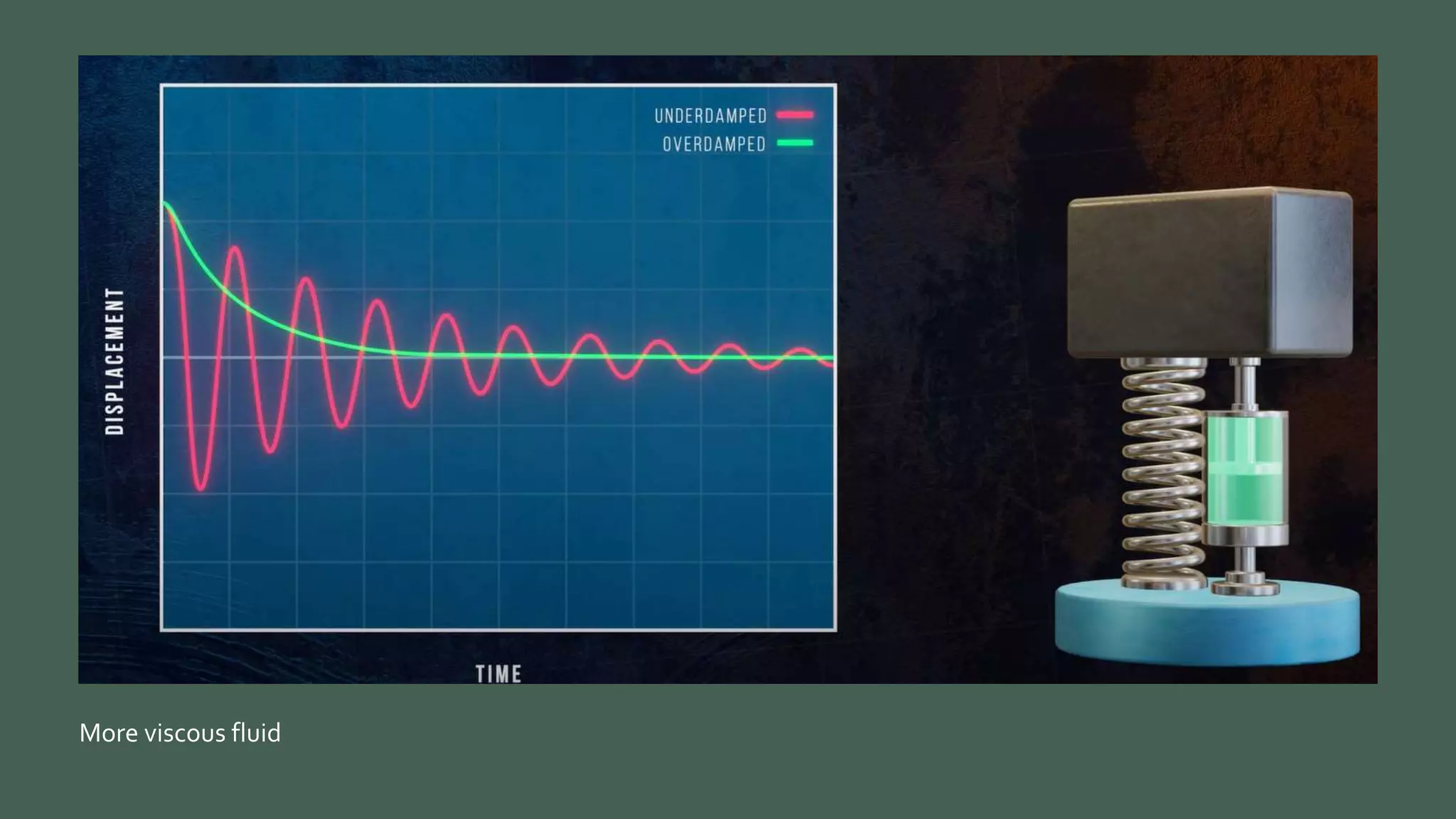
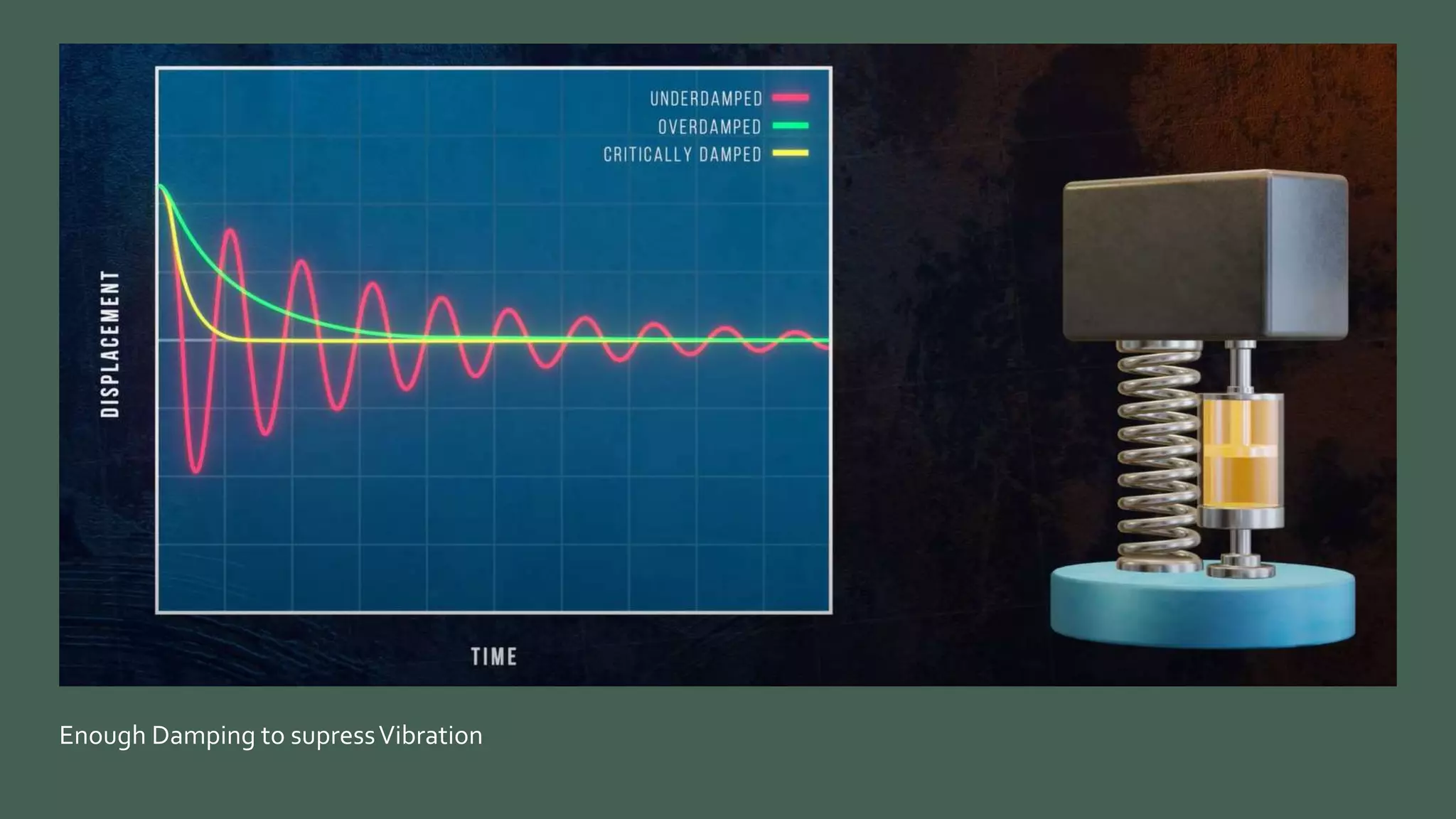
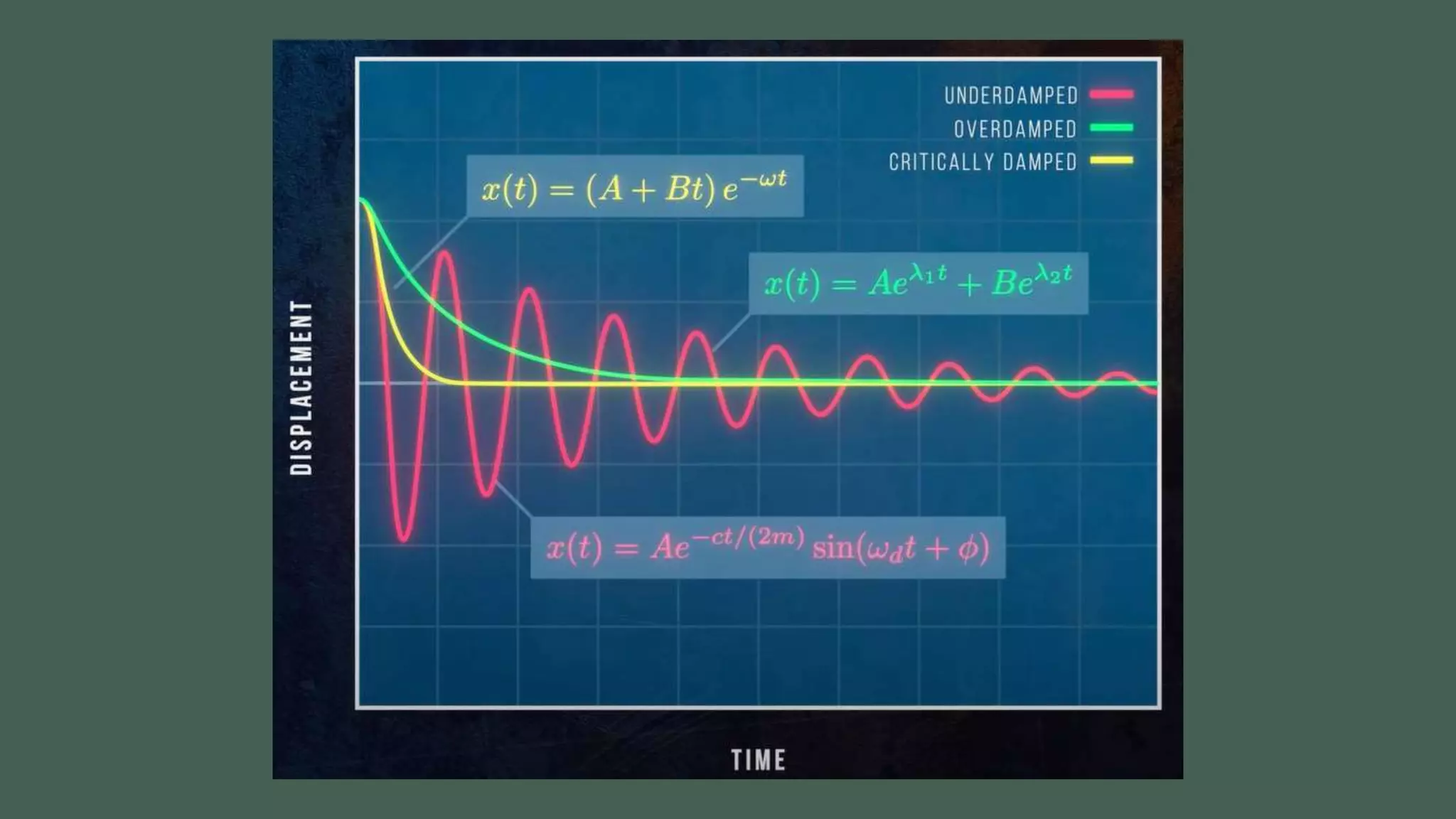
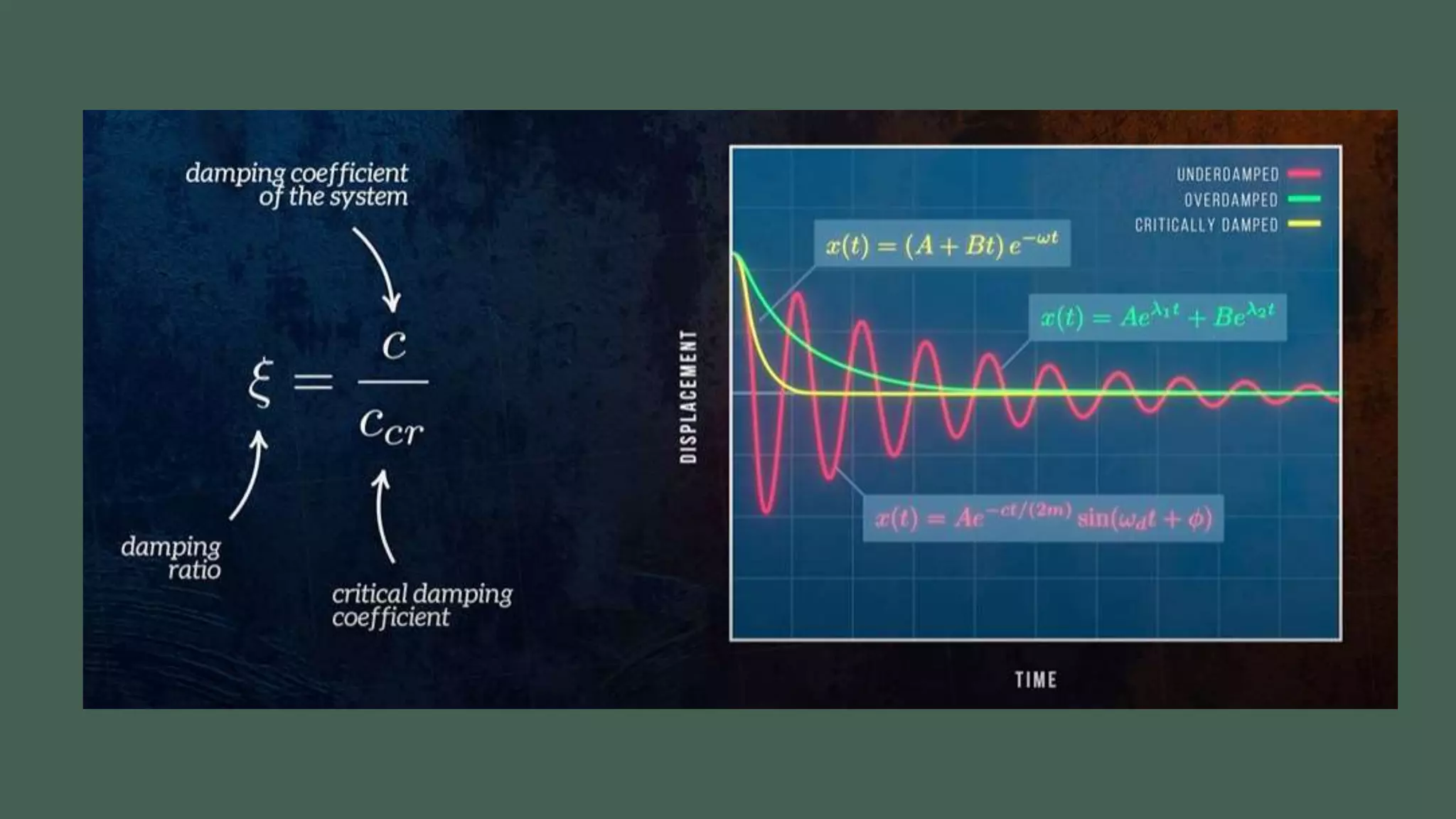
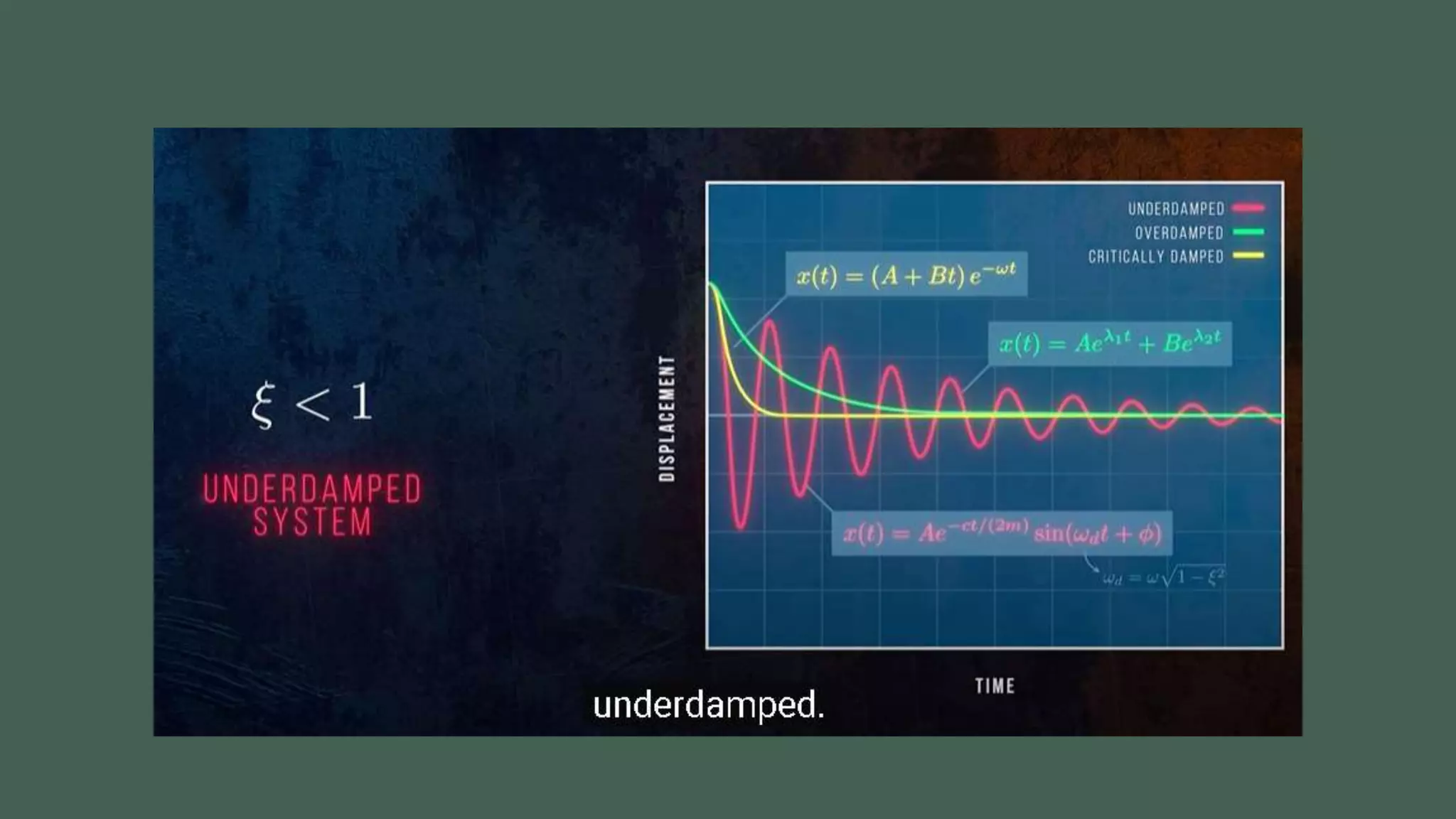
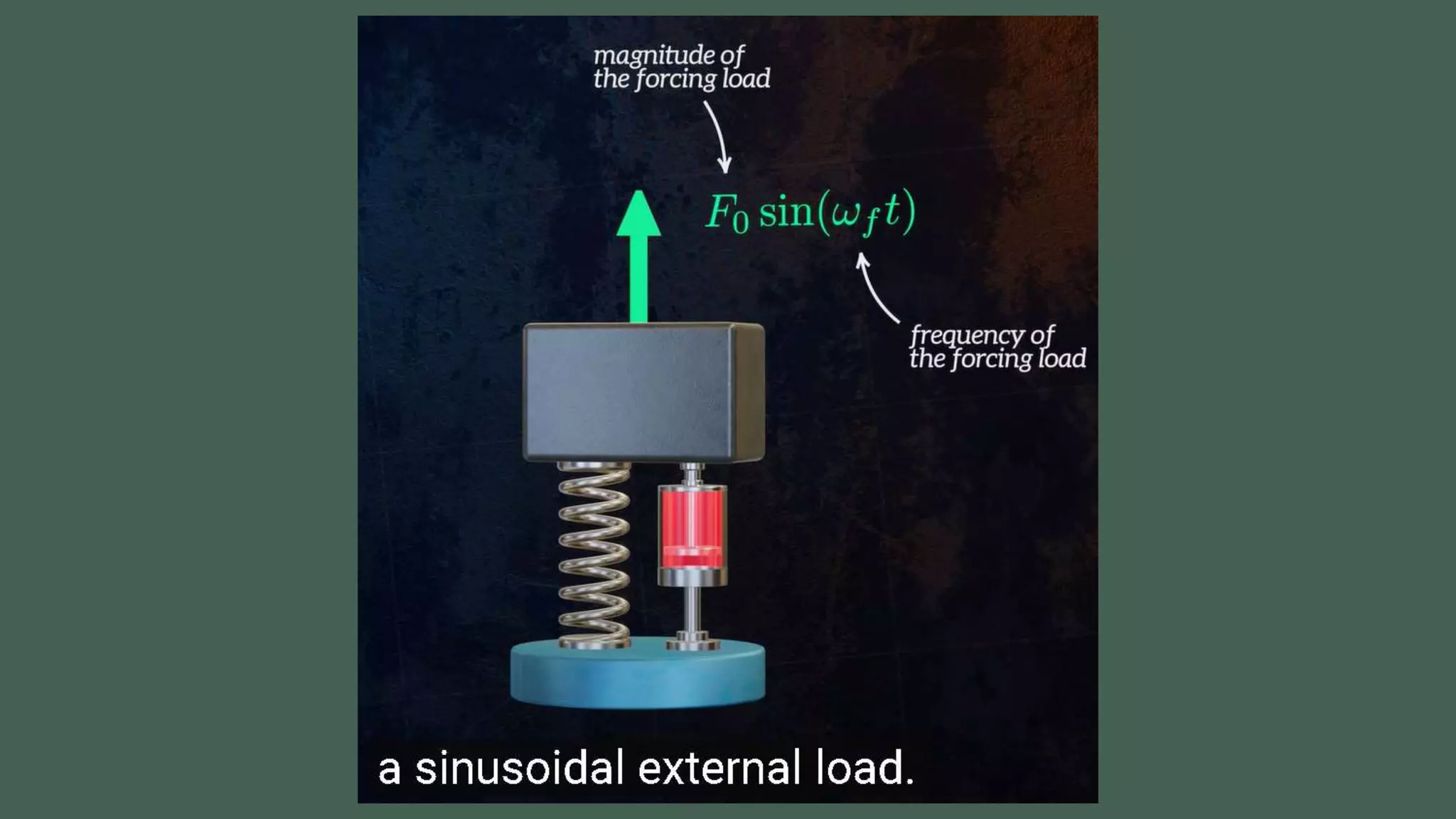
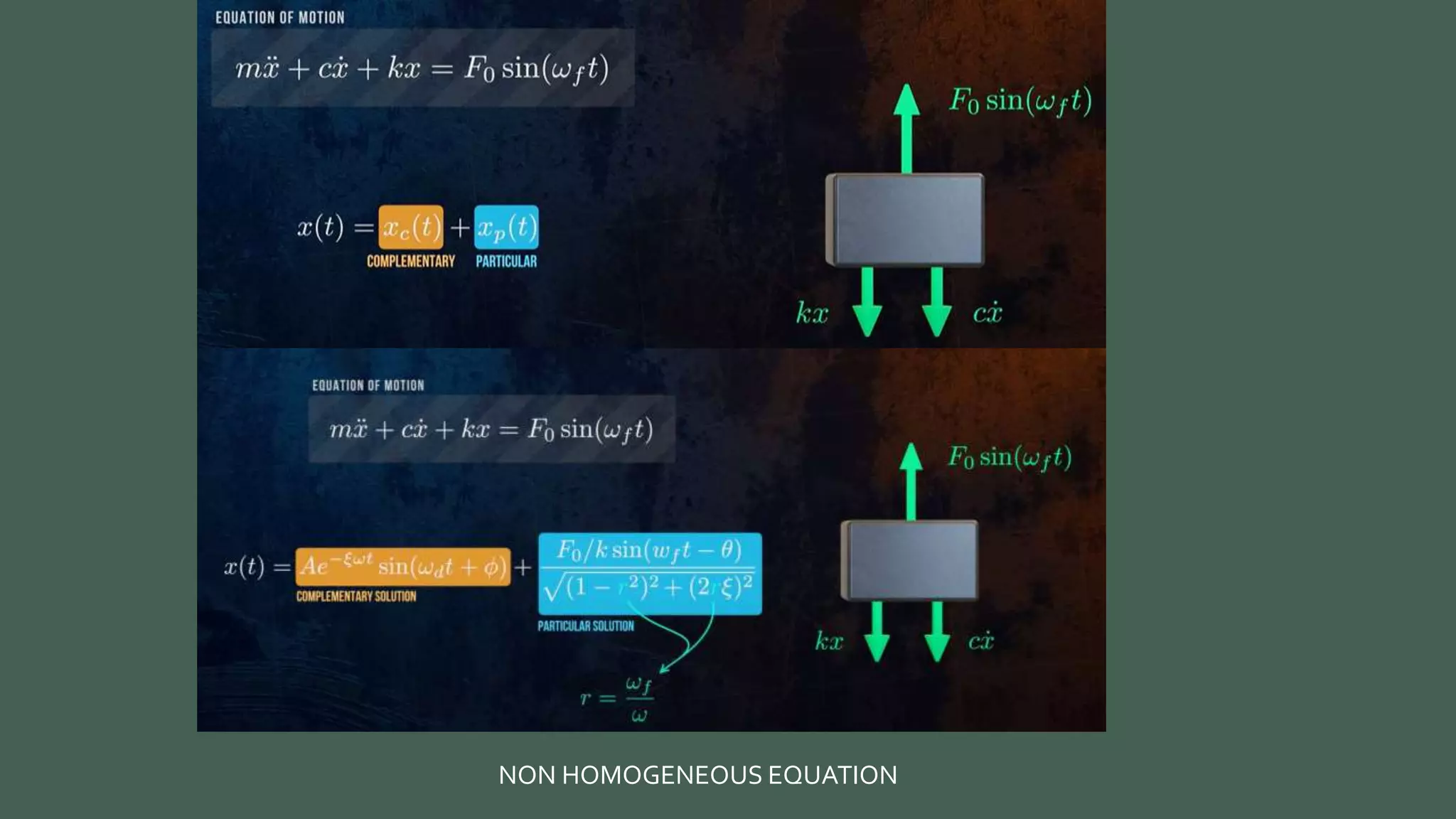
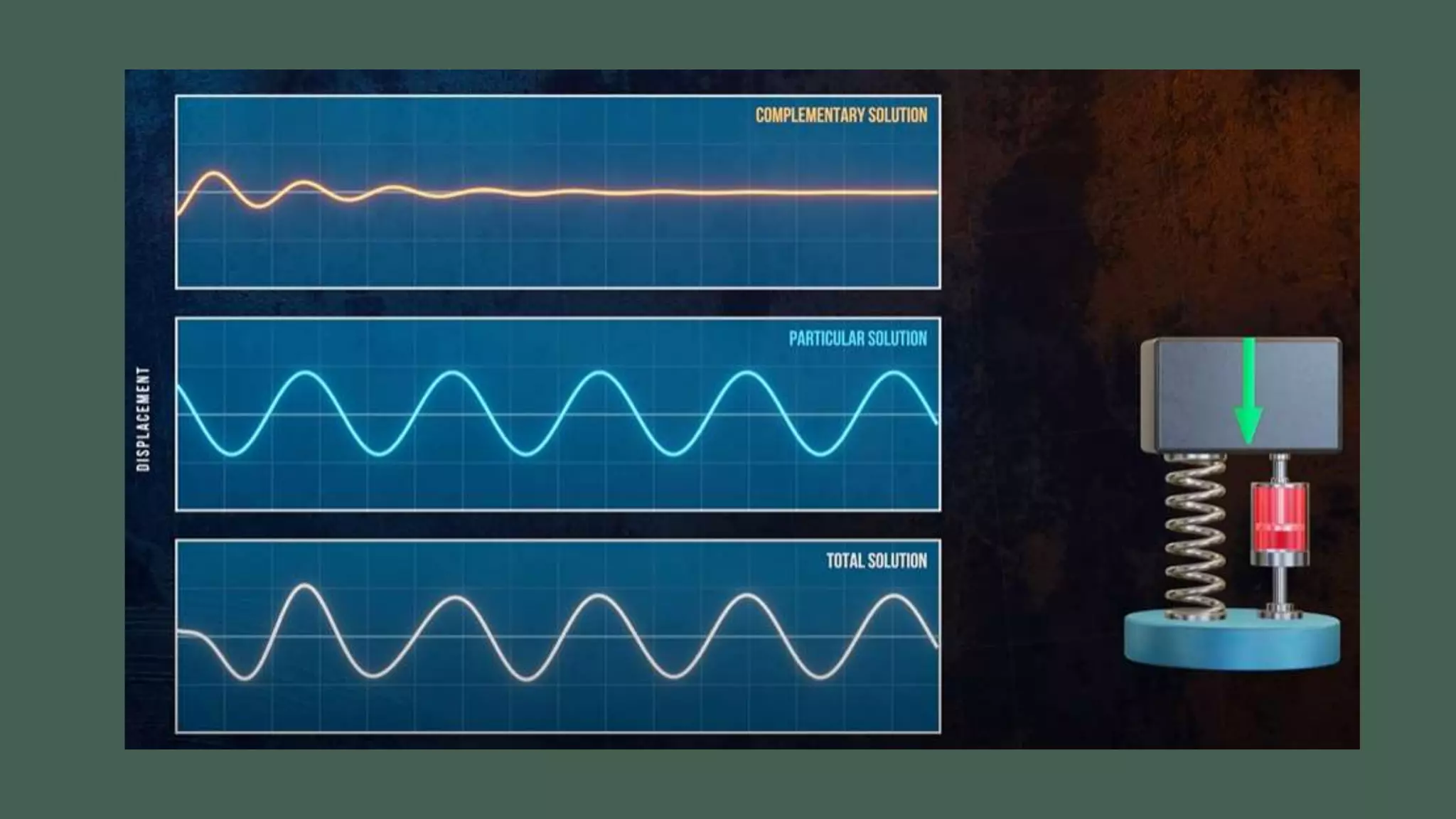
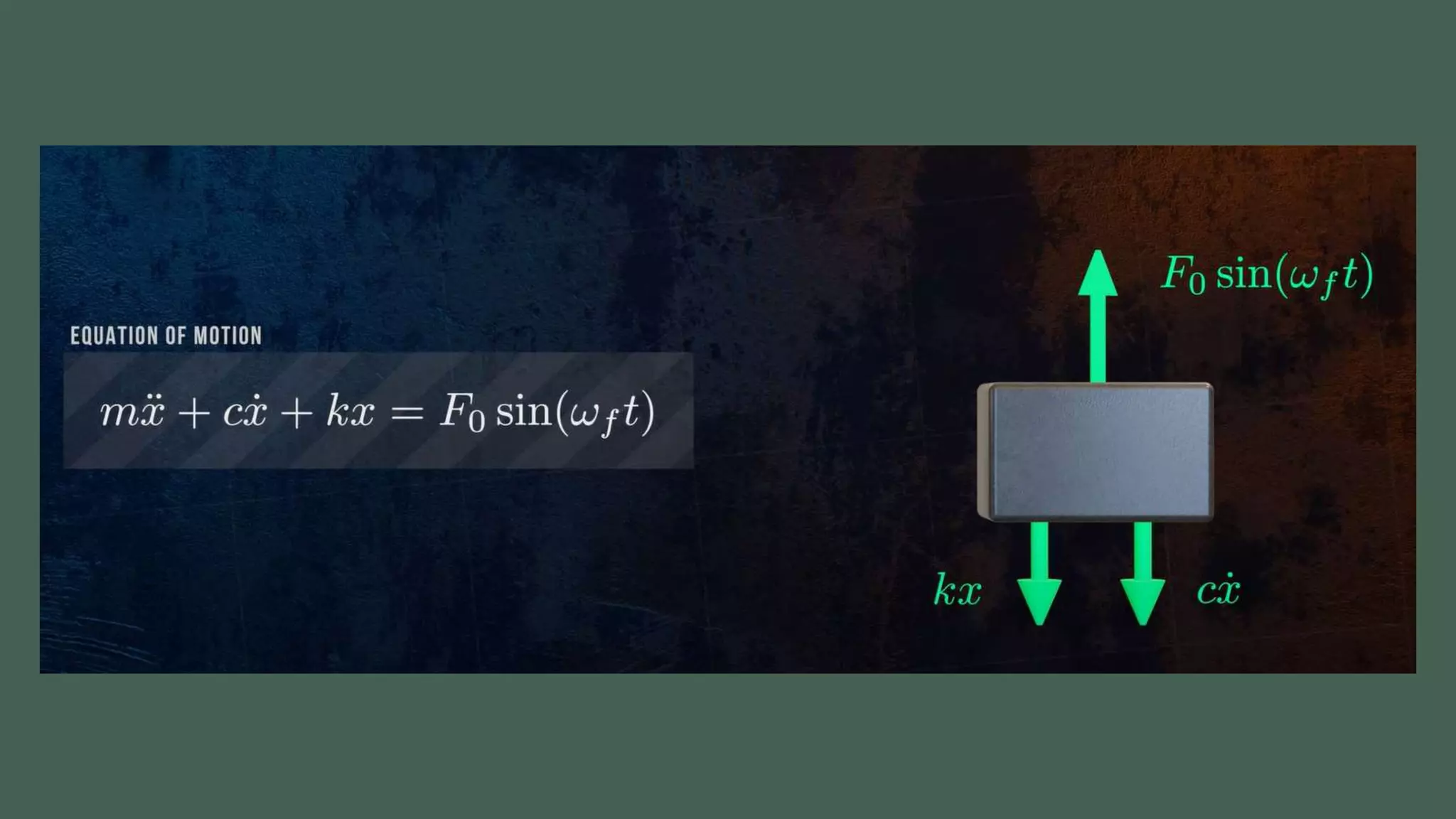
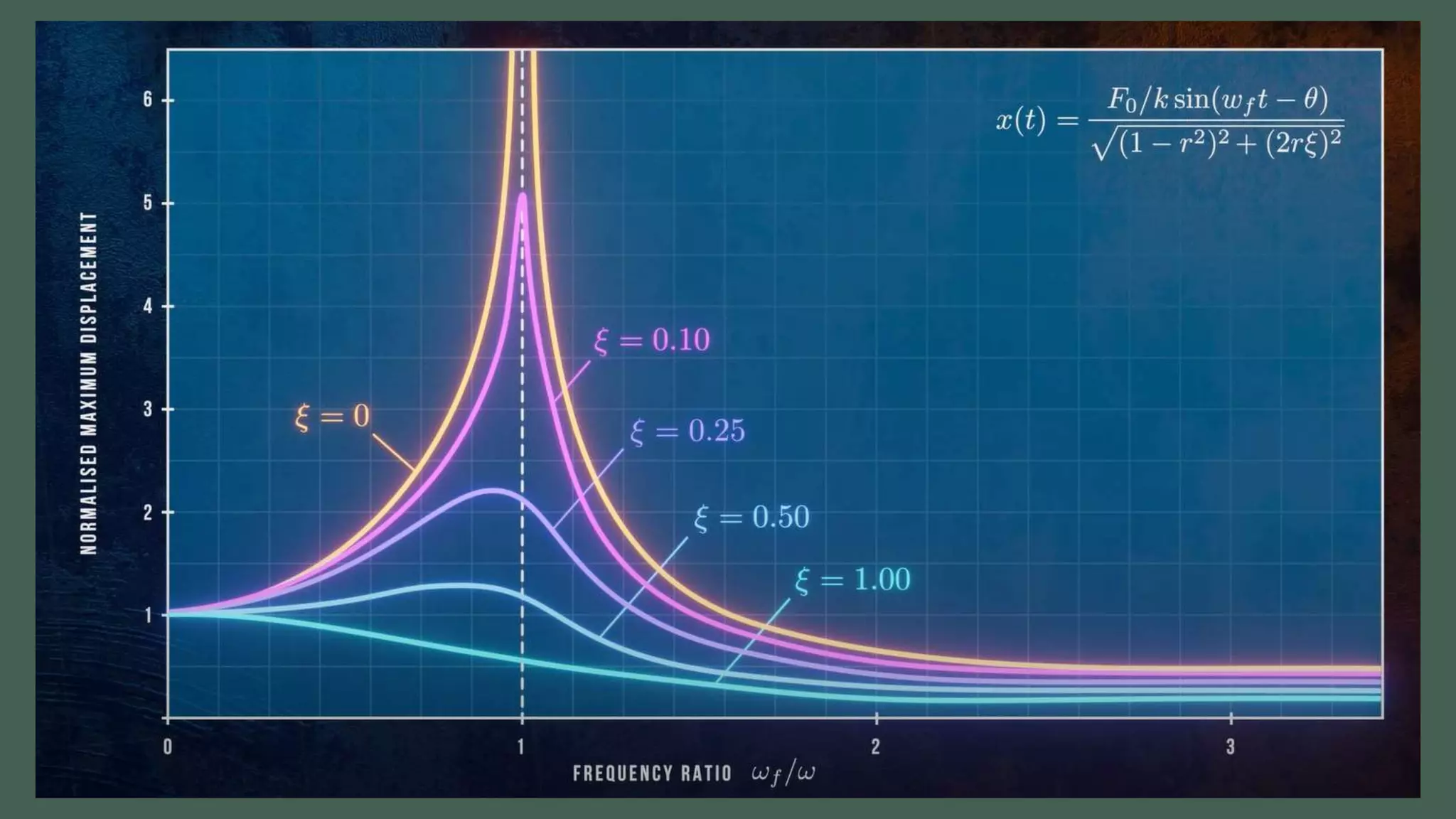
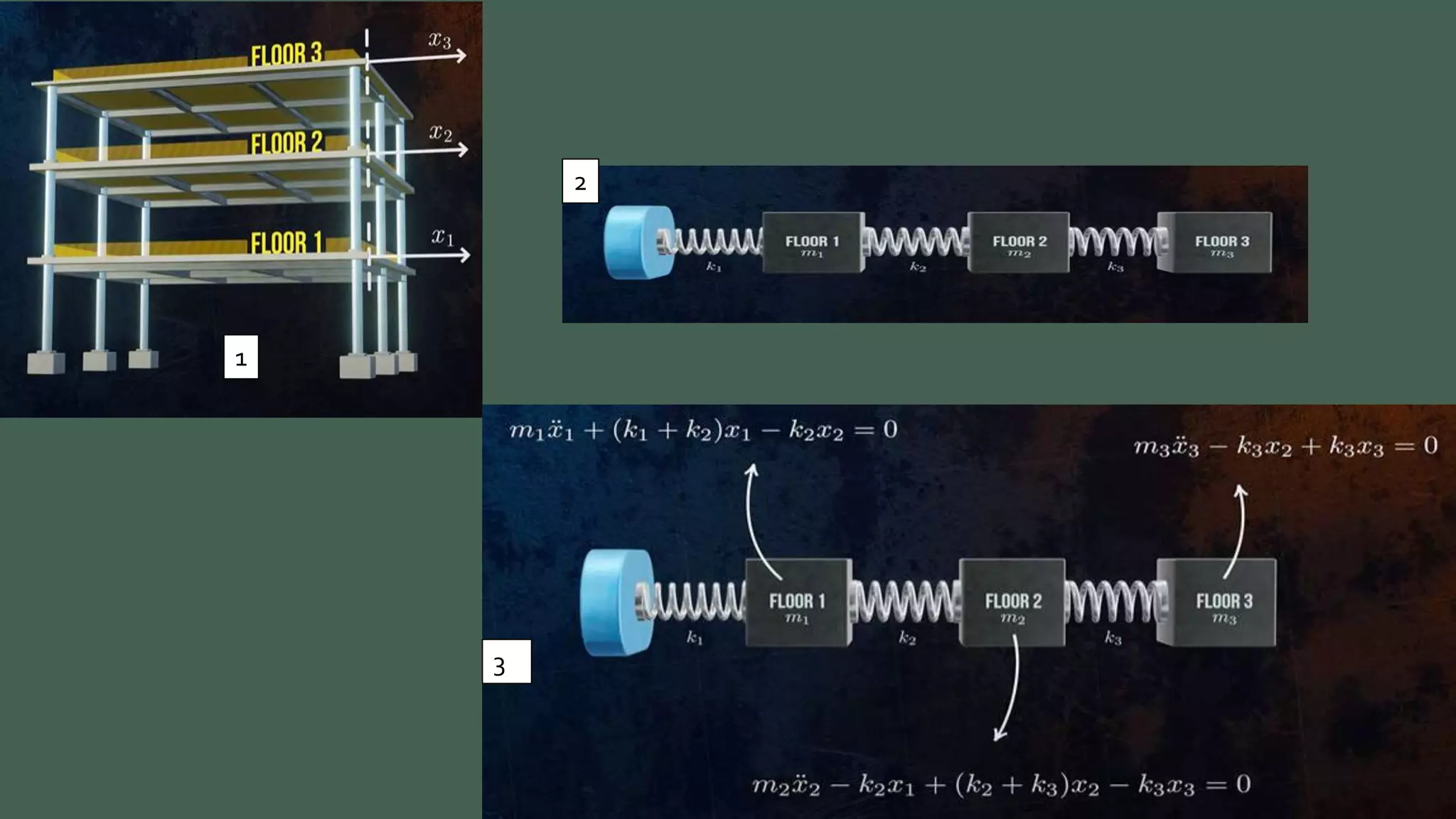
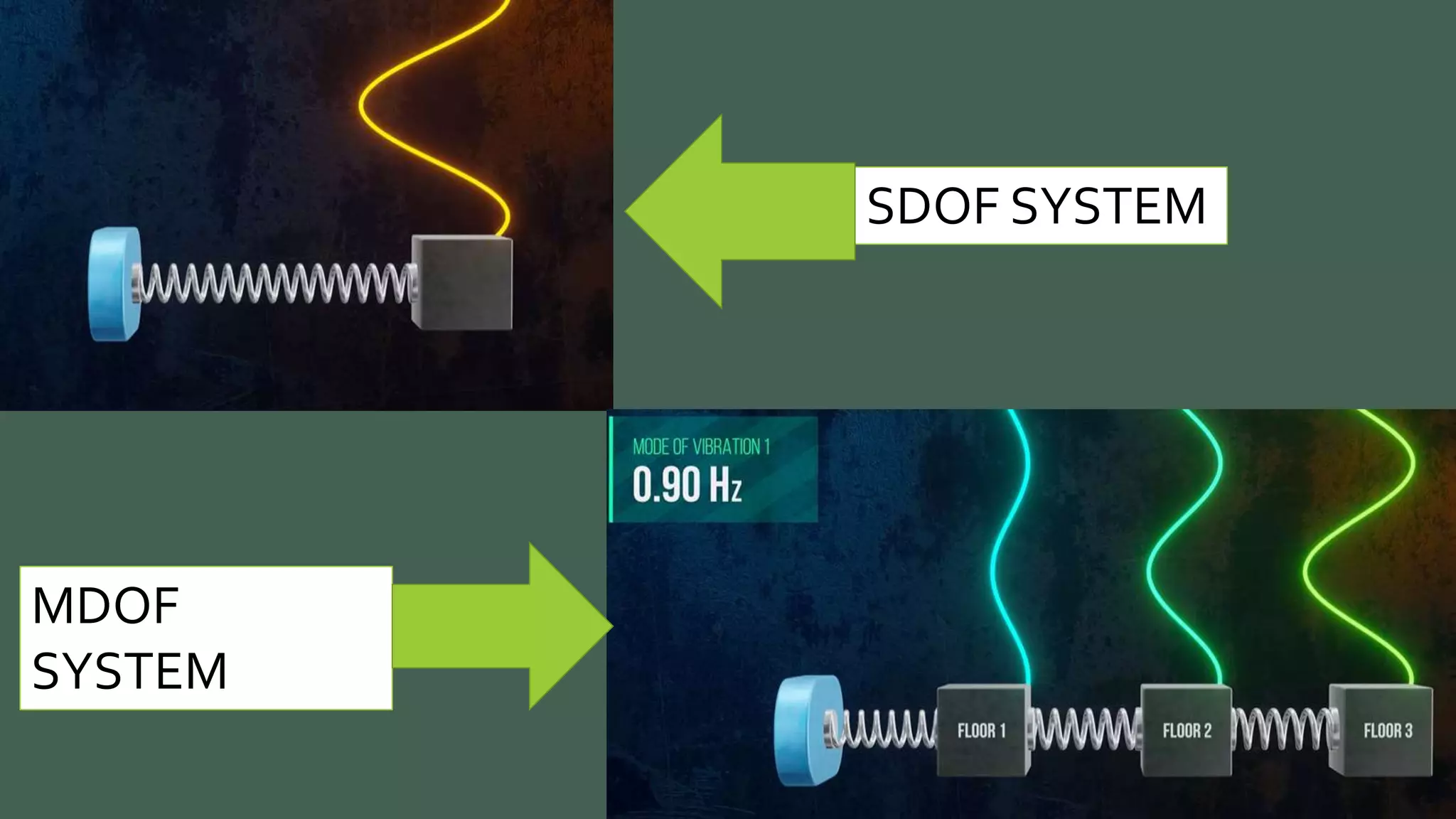
Vibrations are oscillatory motions that can be experienced by structures and systems. There are different types of vibrations including free and forced vibrations. Key aspects of vibrations include amplitude, frequency, and oscillation. Vibrations are modeled using concepts like lumped parameter modeling, which treats a system as a single mass and spring. Resonance occurs when an external force vibrates at the same natural frequency of a structure, causing large oscillations that can damage the structure. The 1940 Tacoma Narrows Bridge collapse was caused by a type of self-excited vibration called aeroelastic flutter under wind loads.